Форма и ширина спектральной линии

1. Оптоэлектронные и квантовые приборы и устройства Лекция 3: Форма и ширина спектральной линии

В.М. Шандаров
Томский государственный университет систем
управления и радиоэлектроники

2. Ширина энергетических уровней

ji
E j Ei
E t h
h
Правило частот
Бора
Соотношение
неопределенностей
2

3. Спектральная линия

I
1
0,5
o
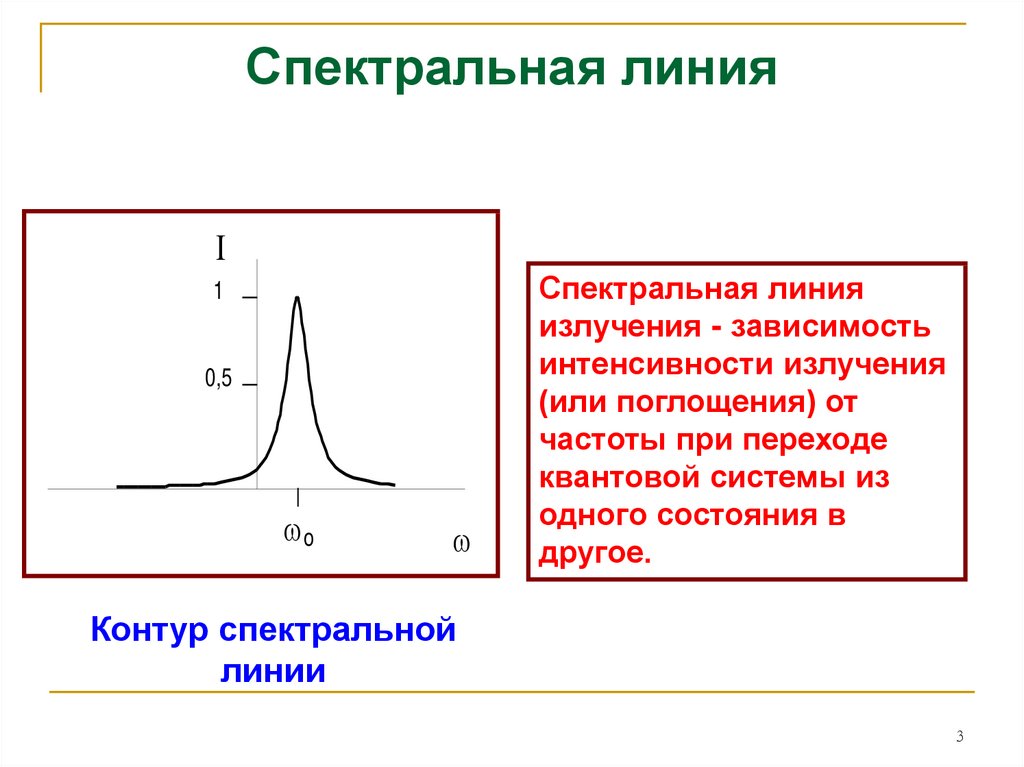
Спектральная линия
излучения - зависимость
интенсивности излучения
(или поглощения) от
частоты при переходе
квантовой системы из
одного состояния в
другое.
Контур спектральной
линии
3

4. Естественная ширина спектральной линии

max min
Ei Ei
h
E – ширина
отдельных
уровней
Неопределенность частоты
перехода между двумя
размытыми уровнями
4

5. Естественная ширина спектральной линии

Естественная ширина спектральной линии
- это ширина спектральной линии
изолированной и неподвижной квантовой
системы. Она минимальна и определяется
временем жизни по спонтанному
излучению.
5

6. Естественная ширина спектральной линии

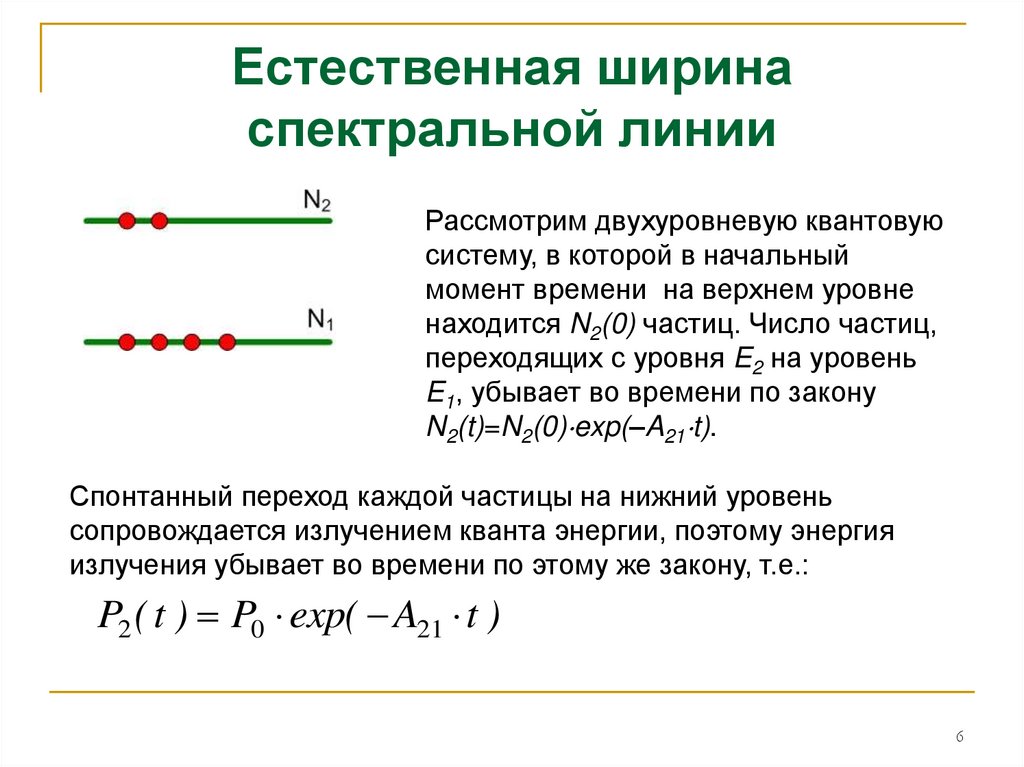
Рассмотрим двухуровневую квантовую
систему, в которой в начальный
момент времени на верхнем уровне
находится N2(0) частиц. Число частиц,
переходящих с уровня E2 на уровень
E1, убывает во времени по закону
N2(t)=N2(0) exp(–A21 t).
Спонтанный переход каждой частицы на нижний уровень
сопровождается излучением кванта энергии, поэтому энергия
излучения убывает во времени по этому же закону, т.е.:
P2 ( t ) P0 exp( A21 t )
6

7. Естественная ширина спектральной линии

Напряженность поля излучения
1
E( t ) ( 2P2 ) 2 cos( 0t ) E0 exp( A21t ) cos( 0t )
где E0=(2P2)1/2.
Излучение может быть представлено в виде затухающего
гармонического колебания E(t), амплитудный спектр которого
g( ) можно найти с помощью интеграла Фурье:
g( ) E( t ) exp( i t )dt
7

8. Естественная ширина спектральной линии

g( )
E0
( 0 )2 ( A21 2 )2
Спектр мощности:
2 P0
G( )
( 0 )2 ( A21 2 )2
8

9. Естественная ширина спектральной линии

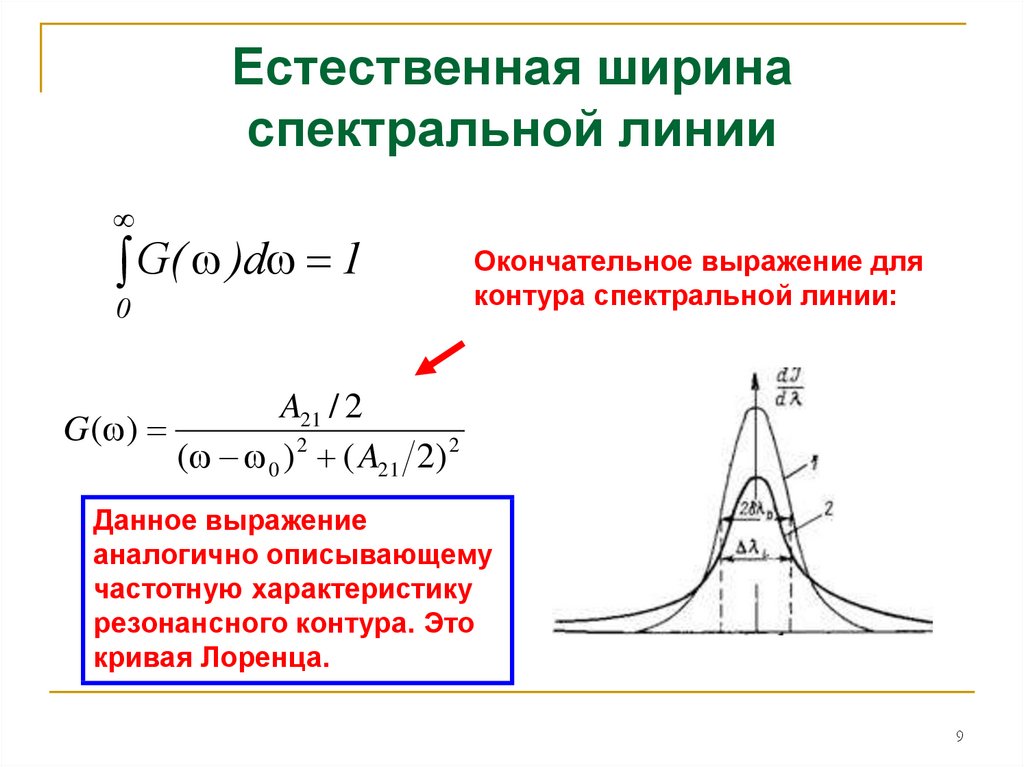
G( )d 1
0
Окончательное выражение для
контура спектральной линии:
A21 / 2
G ( )
( 0 ) 2 ( A21 2) 2
Данное выражение
аналогично описывающему
частотную характеристику
резонансного контура. Это
кривая Лоренца.
9

10. Уширение спектральной линии из-за столкновений

Уширение спектральной линии изза столкновений
Упругие взаимодействия суммарная кинетическая
энергия сталкивающихся
частиц не изменяется
(частицы не обмениваются
внутренней энергией и не
переходят на другие
уровни).
Неупругие столкновения сокращение времени жизни
частиц в данном энергетическом
состоянии до времени среднего
пробега между двумя
столкновениями. Результат –
уширение спектральной линии.
10

11. Уширение спектральной линии из-за столкновений

Уширение спектральной линии изза столкновений
Вероятность столкновения
частиц и, соответственно,
квантовых переходов
одинаковы для всех частиц газа.
Поэтому форма и ширина
спектральной линии всего газа и
каждой частицы одинаковы (и
больше естественной ширины).
Это однородное уширение
спектральной линии.
11

12. Доплеровское уширение спектральной линии

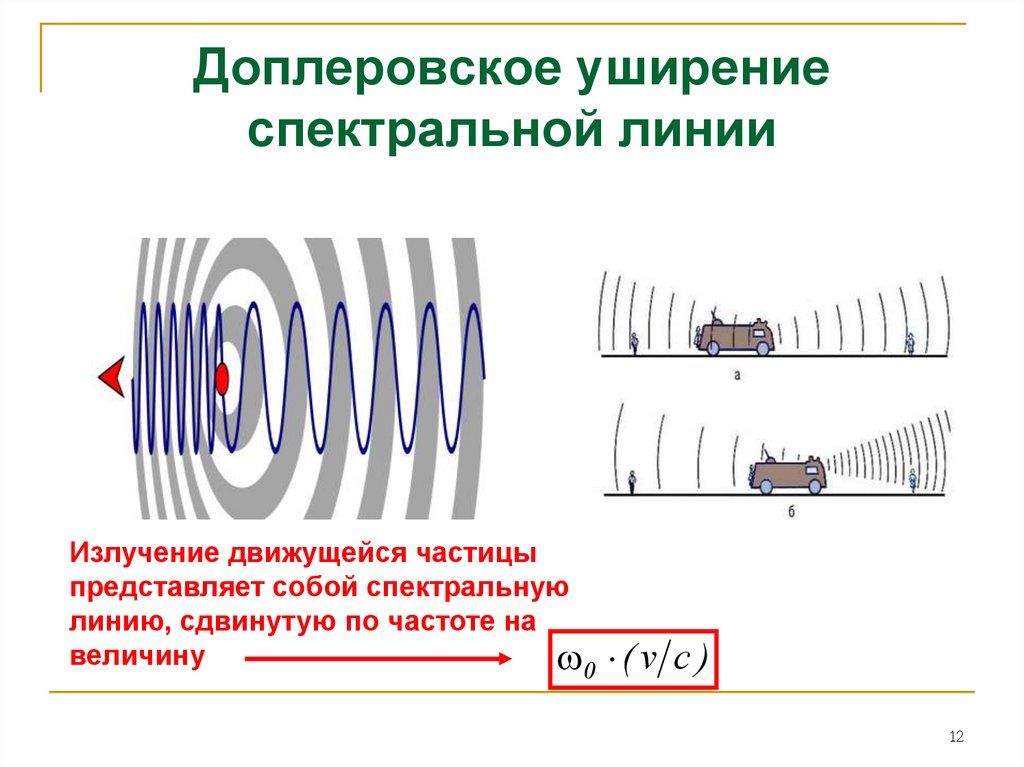
Излучение движущейся частицы
представляет собой спектральную
линию, сдвинутую по частоте на
величину
0
( v c )
12

13. Доплеровское уширение спектральной линии

Линия называется неоднородно уширенной, если она
представляет собой суперпозицию нескольких
неразрешенных спектральных линий.
Форма линии излучения газа в целом определяется
функцией распределения излучающих частиц по скоростям
f(v), т.к. для каждой частицы
0 (v c)
g( )d f ( v )dv
Форма спектральной
линии
13

14. Доплеровское уширение спектральной линии

Частота излучателя, движущегося со скоростью v в направлении
наблюдателя, равна 0 0 ( v c ) . Выразим отсюда
величины v и dv через и 0:
0
v
c
0
g( )d f ( v )dv
d
dv c
0
0
d
g d f
c c
0
0
14

15. Доплеровское уширение спектральной линии

В газе при термодинамическом равновесии распределение
частиц по скорости подчиняется закону Максвелла Больцмана:
2
v dv
1
f ( v ) dv
exp
v0 v0
v0
2kT
m
среднее значение
скорости частиц в газе
15

16. Доплеровское уширение спектральной линии

В итоге, для спектральной линии получим выражение:
2
1
0 d
g ( )d f (v) dv
exp
D
где
D 0
v
c
Линия с таким профилем называется
доплеровски уширенной линией.
16

17. Доплеровское уширение спектральной линии

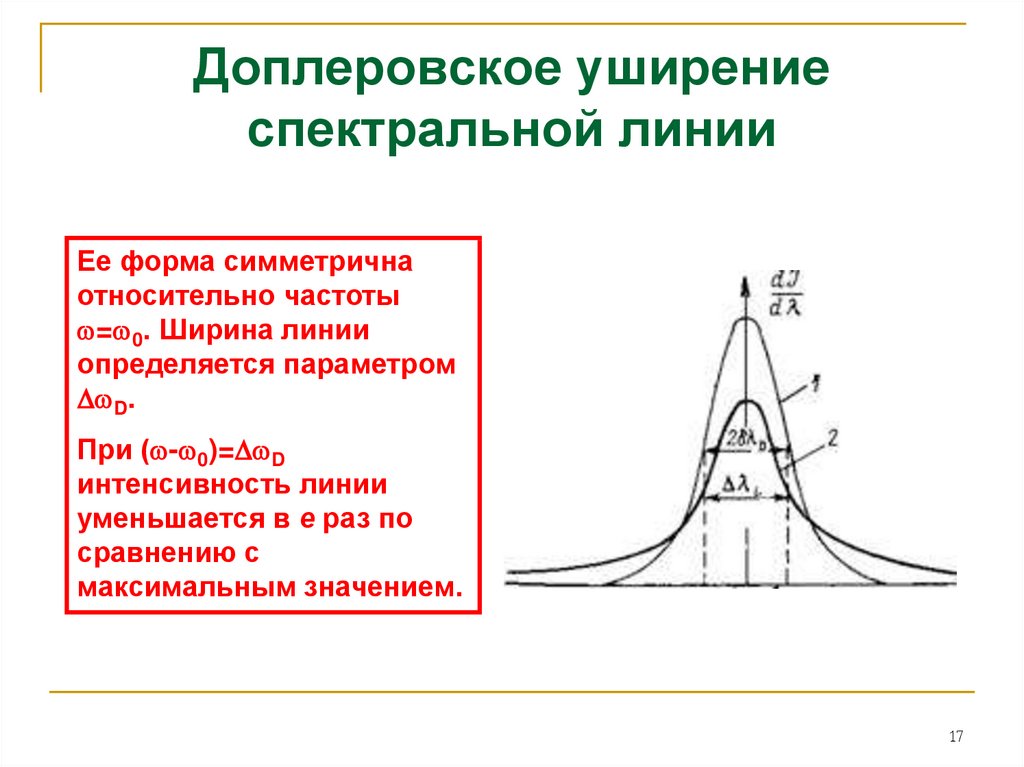
Ее форма симметрична
относительно частоты
= 0. Ширина линии
определяется параметром
D.
При ( - 0)= D
интенсивность линии
уменьшается в е раз по
сравнению с
максимальным значением.
17

18. Доплеровское уширение спектральной линии

Полуширина доплеровски уширенной линии:
/ 2 (ln 2)
1/ 2
D
18

19. Другие механизмы уширения спектральных линий

В твердых веществах уширение спектральных линий
обусловлено иными механизмами:
1. Колебания кристаллической решетки модулируют
внутрикристаллическое электрическое поле в месте
расположения активного иона. Это приводит к модуляции
энергетических уровней иона и уширению спектральной
линии.
2. Ширина линии увеличивается также из-за тепловых
колебаний самих ионов.
19

20. Другие механизмы уширения спектральных линий

3. Пространственная неоднородность физических
параметров среды или неоднородности
электрического и магнитного полей также могут
приводить к уширению спектральных линий в
твердотельных средах.
20

21. Отрицательная температура (инверсия населенностей)

Возможность усиления и генерации
электромагнитных колебаний в квантовых
системах определяется возможностью
индуцированных переходов в среде под
воздействием электромагнитного поля.
21

22. Отрицательная температура (инверсия населенностей)

При взаимодействии квантовой системы с
электромагнитным полем происходят и
переходы с поглощением энергии, а также
возможны релаксационные, безызлучательные
переходы.
22

23. Отрицательная температура (инверсия населенностей)

Рассмотрим обмен энергии между полем и
простейшей двухуровневой квантовой
системой.
Пусть двум энергетическим уровням E1 и E2
соответствуют населенности N1 и N2, а частота
внешнего поля вн удовлетворяет условию:
вн= 12,
где 12 – центральная частота спектральной
линии.
23

24. Отрицательная температура (инверсия населенностей)

Число вынужденных переходов с излучением
энергии в единице объема равно:
n21 B U N 2
Мощность электромагнитного излучения Pвыд,
выделяемая при этом в единице объема, равна:
Pвыд n21h 12 B U N 2 h 12
24

25. Отрицательная температура (инверсия населенностей)

Число вынужденных переходов с поглощением
энергии и поглощаемая в единице объема
мощность внешнего электромагнитного поля Pпогл
равны:
n12 B U N 1
Pïîãë n21 h 12 BU N1h 12
25

26. Отрицательная температура (инверсия населенностей)

Изменение мощности внешнего
электромагнитного поля определяется
разностью выделяемой и поглощаемой
мощностей:
P Pвыд Pпог л BU h 12 ( N 2 N 1 )
Величину P называют мощностью
взаимодействия. Если P›0, то в квантовой системе
происходит усиление внешнего электромагнитного
поля, а при P‹0 это поле ослабляется
26

27. Отрицательная температура (инверсия населенностей)

Итак, условием усиления электромагнитного поля
при взаимодействии с квантовой системой
являются соотношения:
( N2 N2 ) 0
или
N2
1
N1
27

28. Отрицательная температура (инверсия населенностей)

В состоянии термодинамического равновесия
населенности разных уровней определяются
законом Больцмана
E
N m N0 exp
kT
При этом всегда выполняется условие N2 ‹ N1 или:
N2
E2 E1
exp
N1
kT
28

29. Отрицательная температура (инверсия населенностей)

Это выражение определяет соотношение
населенностей энергетических уровней, но
формально оно может рассматриваться и как
соотношение, определяющее значение
абсолютной температуры по величинам
населенностей разных энергетических уровней
системы, находящейся в состоянии
термодинамического равновесия.
29

30. Отрицательная температура (инверсия населенностей)

Приведем его к виду:
E2 E1
h 21
Tп
k ln N1 / N 2 k ln N1 / N 2
величину Tn здесь называют температурой
перехода
В состоянии термодинамического равновесия
› N2 , т.е. Tn › 0
N1
30

31. Отрицательная температура (инверсия населенностей)

Состояние с N2›N1 является обратным, т.е.
инверсным. Поэтому состояние с N2›N1, когда в
квантовой системе возможно усиление
электромагнитного излучения, называется
состоянием с инверсией населенности или просто
инверсией населенности. При N2›N1 видим, что Tn‹0.
Поэтому состояние с инверсией населенностей
уровней иногда называют состоянием с
отрицательной температурой.
31

32. Отрицательная температура (инверсия населенностей)

Таким образом, условие усиления в квантовой
системе можно выразить и в форме:
Tn‹0
Среда, в которой возможна инверсия
населенности или состояние с отрицательной
температурой, называется активной средой.
32

33. Отрицательная температура (инверсия населенностей)

Температура перехода совпадает с реальной
температурой только в состоянии
термодинамического равновесия.
Условие N2›N1, при котором Tn‹0, вовсе не означает,
что абсолютная температура среды действительно
меньше нуля.
33

34. Отрицательная температура (инверсия населенностей)

При термодинамическом равновесии N1›N2, поэтому n12›n21.
Соответственно, N1 при наличии резонансного внешнего
поля убывает, а N2 – возрастает. При достаточно большом
значении Uν может быть достигнуто условие N2=N1. При этом
число переходов частиц с излучением и поглощением
энергии уравнивается (n12=n21) и наступает динамическое
равновесие.
Данный режим называется насыщением перехода.
Но дальнейшее увеличение плотности мощности
электромагнитного поля Uν все равно не может привести к
инверсии населенностей.
34

35. Отрицательная температура (инверсия населенностей)

Итак, при воздействии на двухуровневую
квантовую систему электромагнитного поля
можно достичь насыщения перехода, но не
инверсии населенностей.
35

36. Инверсия населенностей

Для более строгого анализа взаимодействия
электромагнитного поля с двухуровневой квантовой
системой необходимо учитывать также наличие спонтанных
и безызлучательных переходов. Величины населенностей
уровней при этом могут быть найдены из решения
кинетических уравнений. Для двухуровневой системы эти
уравнения имеют вид:
dN1
N1 BU N1w12 N 2 BU N 2 A21 N 2 w21
dt
dN2
N1 BU N1w12 N 2 BU N 2 A21 N 2 w21
dt
N1 N 2 N
36

37. Инверсия населенностей

При сохранении полного числа частиц N для двухуровневой
системы
dN1
dN2
dt
dt
Для стационарного состояния системы имеем:
dN1 dN2
0
dt
dt
N 1 ( BU w12 ) N 2 ( BU A21 w21 ) 0
N1 N 2 N
37

38. Инверсия населенностей

Решая систему двух этих уравнений, можно получить:
N1( BU w12 ) N 2 ( BU A21 w21 ) N ( BU A21 w21 ) 0
или
N ( BU A21 w21 )
A21 w21 BU
N
N1
2 BU A21 w12 w21 A21 w12 w21
1 12 U
где
2B
12
A21 w12 w21
38

39. Инверсия населенностей

Аналогично
N
w12 BU
N2
A21 w12 w21 1 12 U
Разность и отношение этих величин даются
выражениями:
N w12 A21 w21
1
N 2 N1
A21 w12 w21
1 12 U
N1 A21 w21 BU
N2
w12 BU
39

40. Инверсия населенностей

Мощность взаимодействия,
введенная ранее, может быть
выражена в виде:
P h 21 BU ( N 2 N1 ) h 21 B N
U
w12 ( A21 w21 )
A21 w12 w21 1 12 U
40

41.

СПАСИБО ЗА ВНИМАНИЕ!
41