Similar presentations:
Система задач на тему двугранный угол
1.
2.
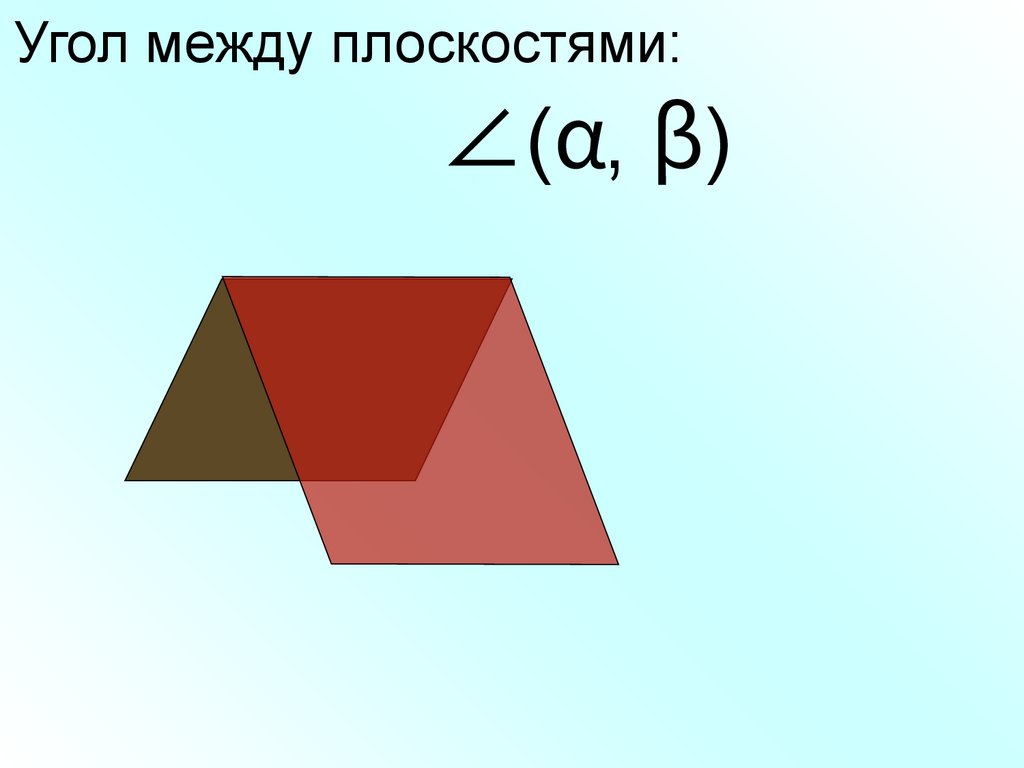
Угол между плоскостями:∠(α, β)
3.
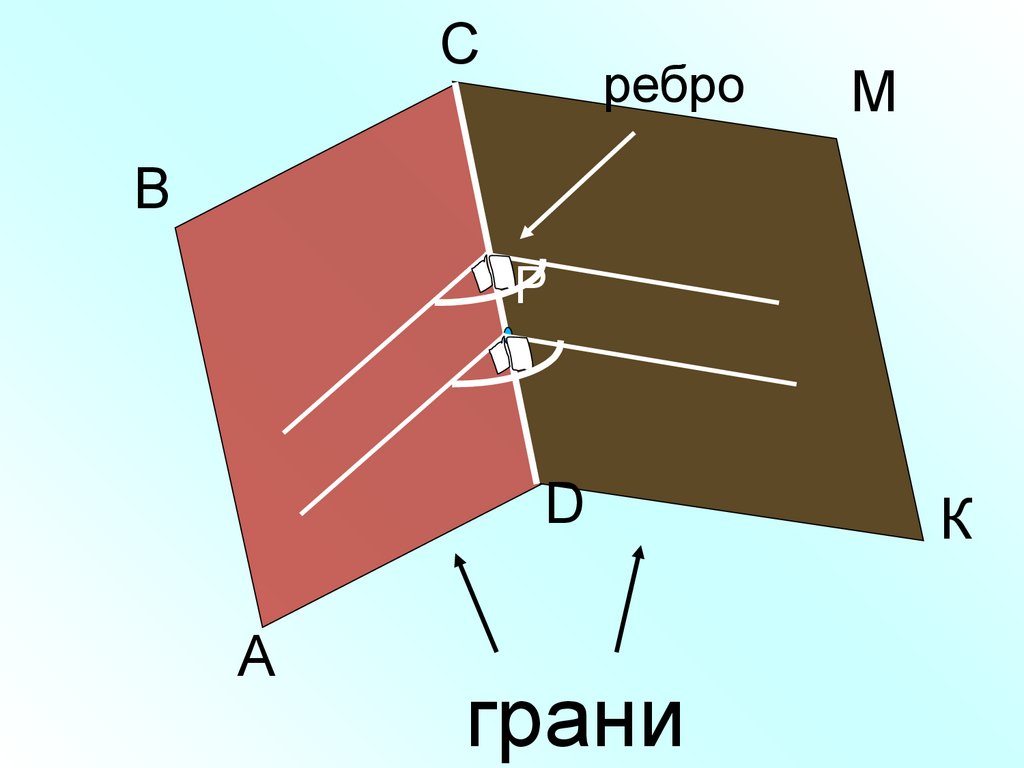
Сребро
М
В
Р
D
А
грани
К
4.
РВ
А
D
К
∠(α, β)
С
=
∠АВСМ
=
∠Р
М
5.
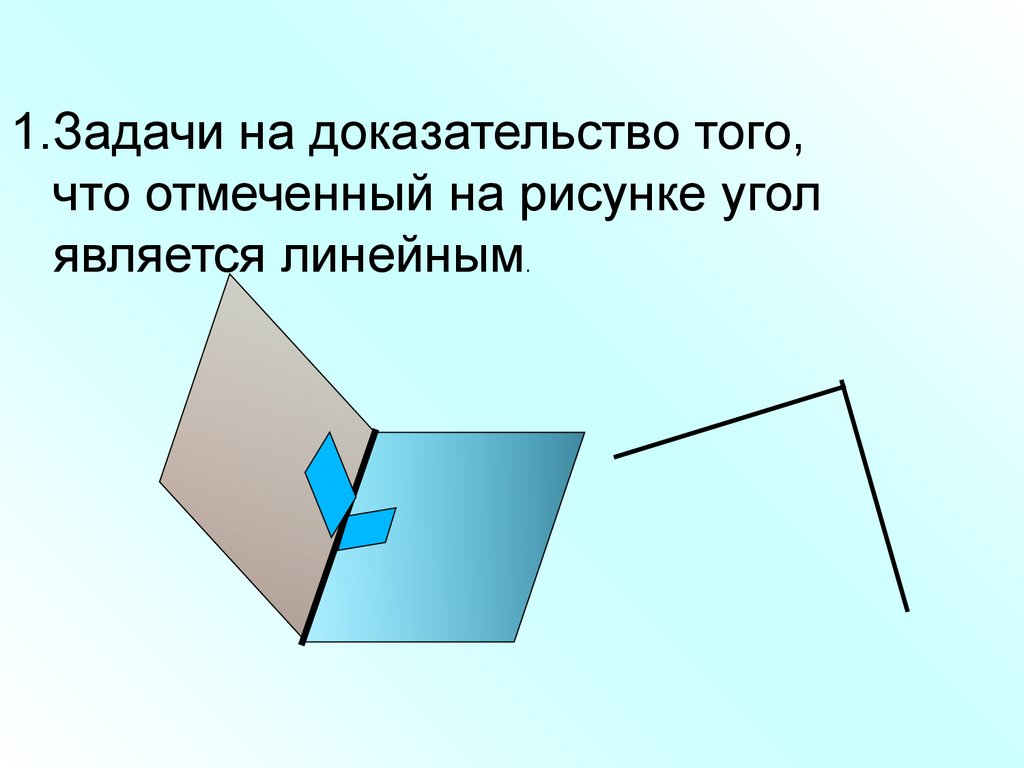
1.Задачи на доказательство того,что отмеченный на рисунке угол
является линейным.
6.
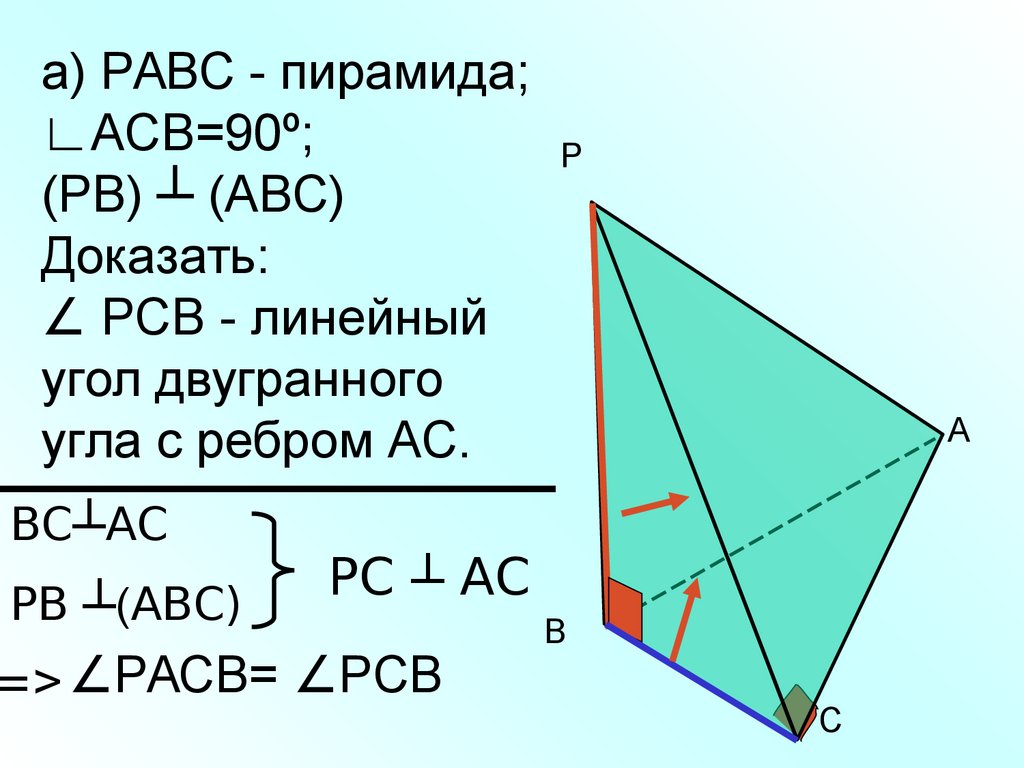
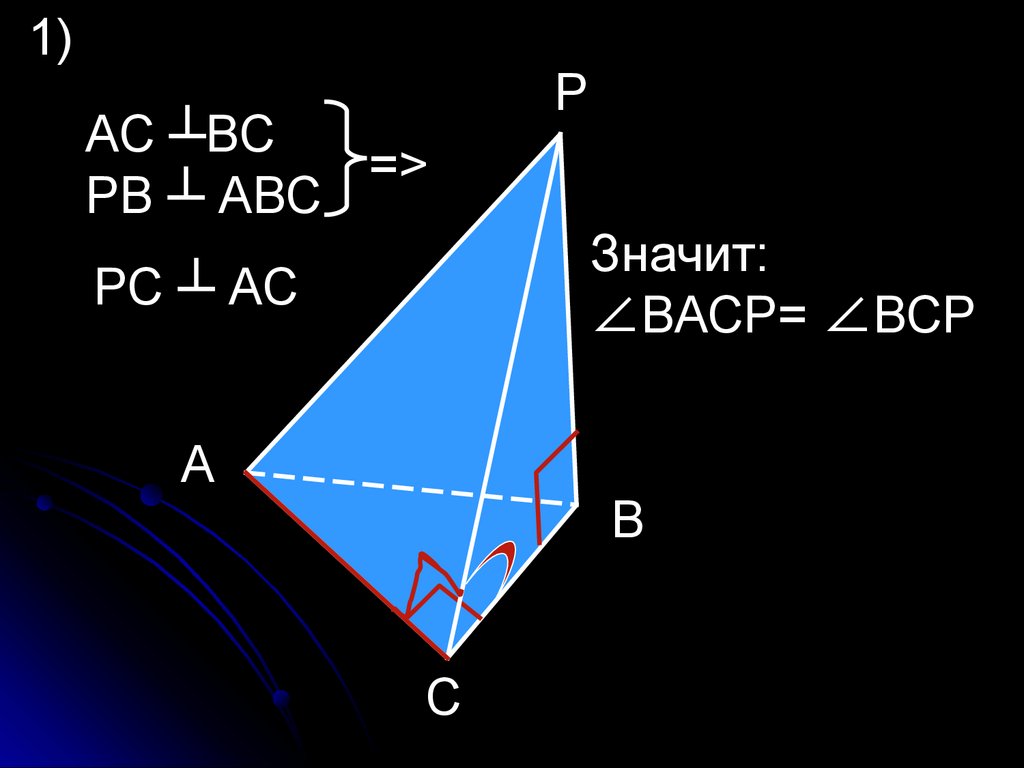
а) РАВС - пирамида;∟АСВ=90º;
(РВ) ┴ (АВС)
Доказать:
∠ РСВ - линейный
угол двугранного
угла с ребром АС.
ВС┴АС
РВ ┴(АВС)
Р
А
РС ┴ АС
=> ∠РАСВ= ∠РСВ
В
С
7.
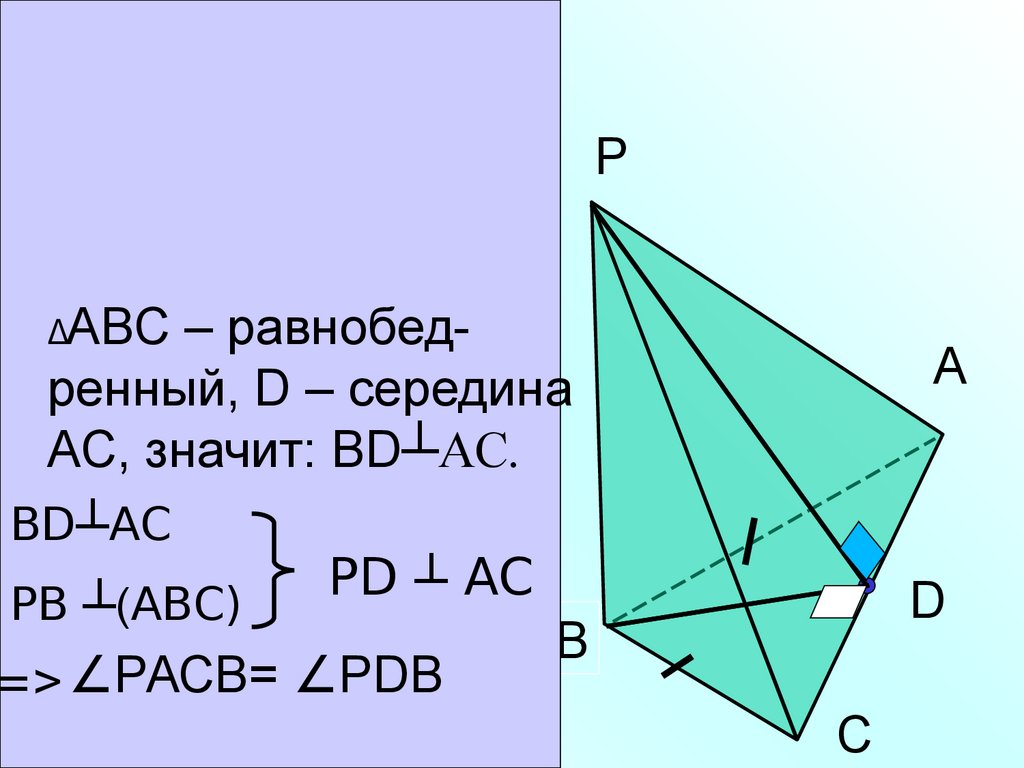
в) РАВС - пирамиDа;АВ=ВС; D- сереDина
Р
АС;
(РВ) ┴ (АВС);
Dоказать:
ΔАВС – равнобед∟РDВ - линейный
ренный, D – середина
угол Dвугранного
АС,
значит:
ВD┴АС.
угла с ребром АС.
ВD┴АС
РD
┴ АС
РВ ┴(АВС)
=> ∠РАСВ= ∠РDВ
А
D
В
С
8.
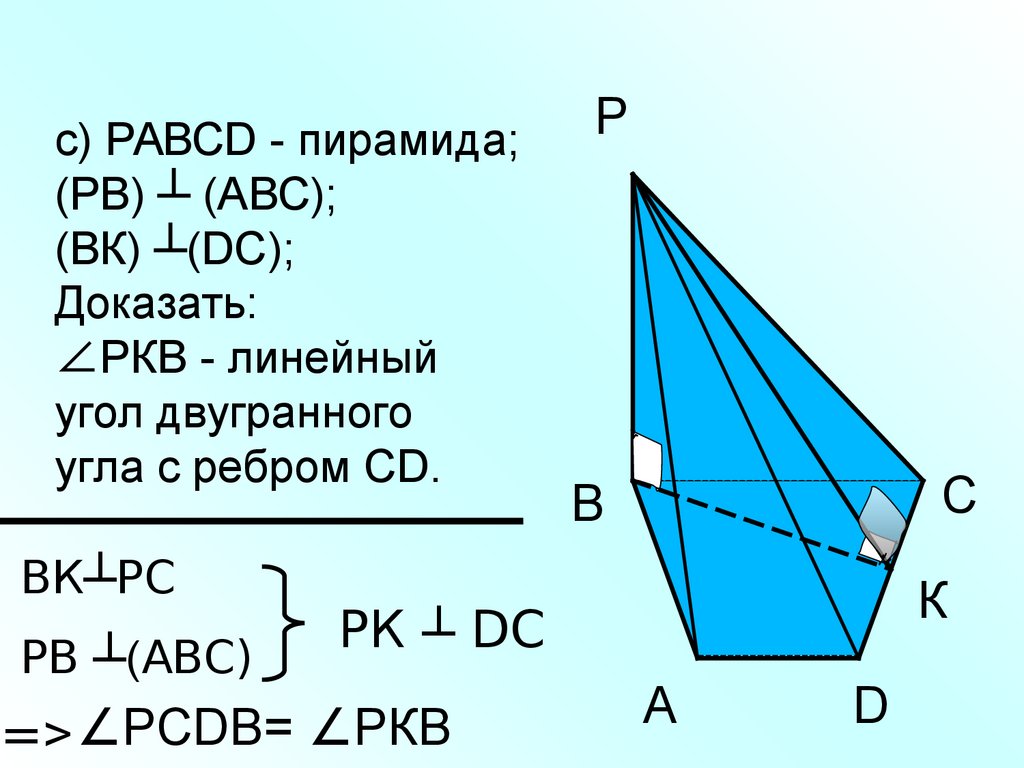
с) РАВСD - пирамида;(РВ) ┴ (АВС);
(ВК) ┴(DС);
Доказать:
∠РКВ - линейный
угол двугранного
угла с ребром СD.
ВК┴РС
РВ ┴(АВС)
Р
С
В
К
РК ┴ DС
=> ∠РСDВ= ∠РКВ
А
D
9.
2. Задачи на выделениелинейного угла
среди нескольких обозначенных
на рисунке углов.
10.
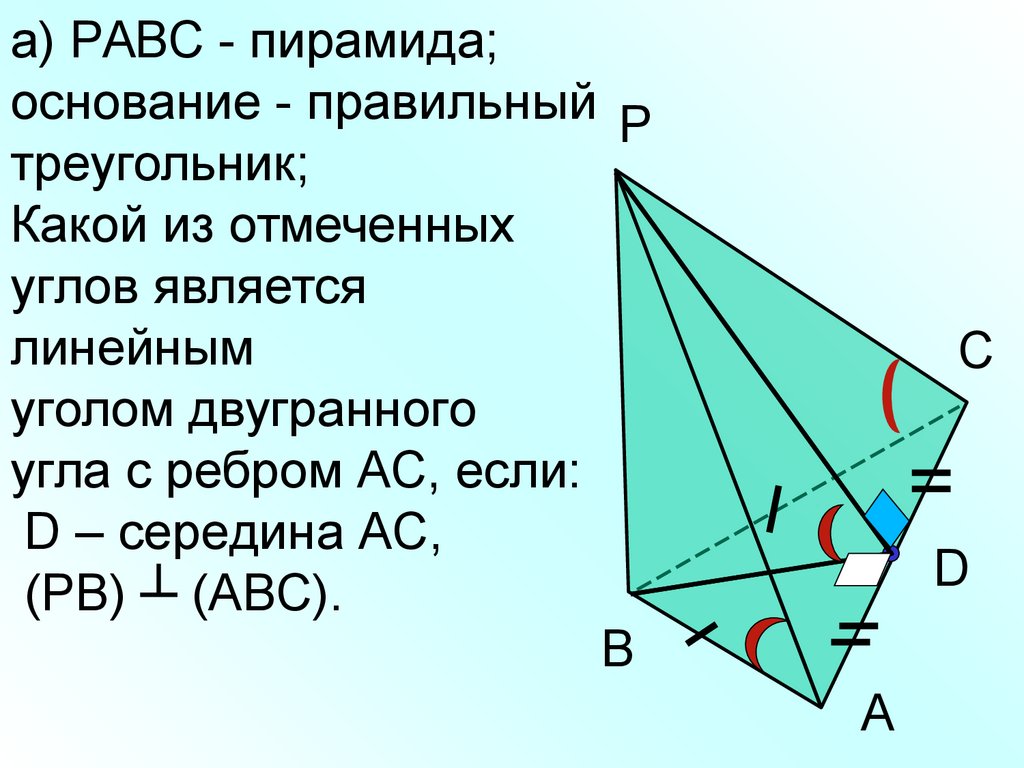
а) РАВС - пирамида;основание - правильный Р
треугольник;
Какой из отмеченных
углов является
линейным
уголом двугранного
угла с ребром АС, если:
D – середина АС,
(РВ) ┴ (АВС).
В
С
D
А
11.
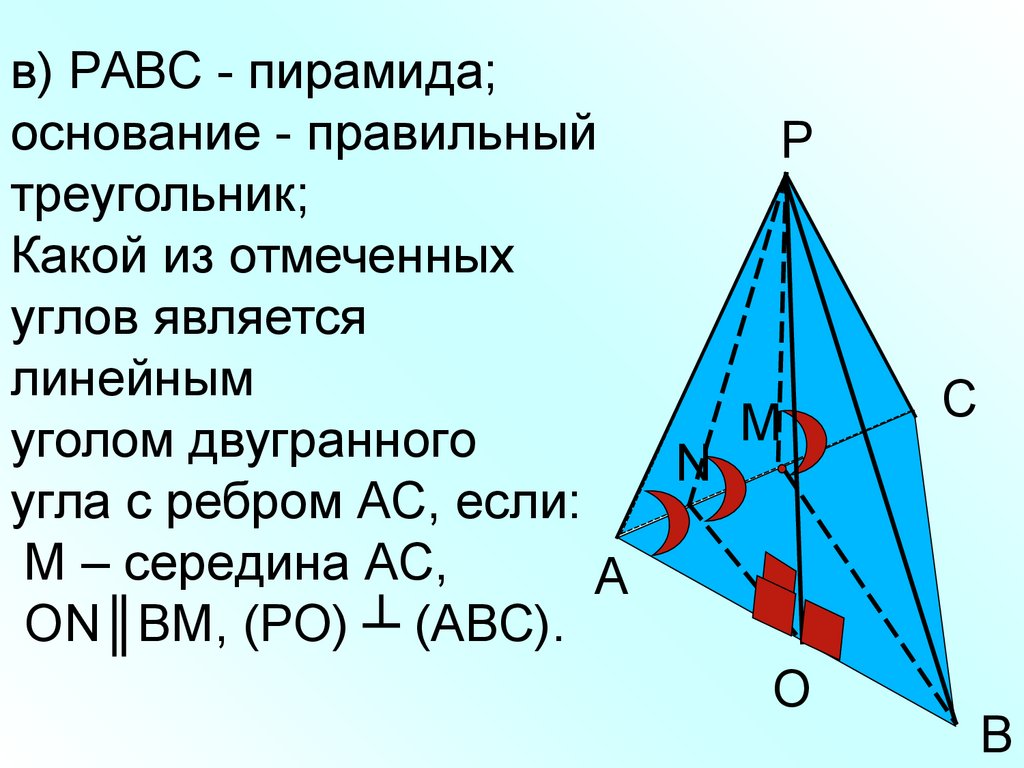
в) РАВС - пирамида;основание - правильный
Р
треугольник;
Какой из отмеченных
углов является
линейным
М
уголом двугранного
N
угла с ребром АС, если:
М – середина АС,
А
ОN║ВМ, (РО) ┴ (АВС).
О
С
В
12.
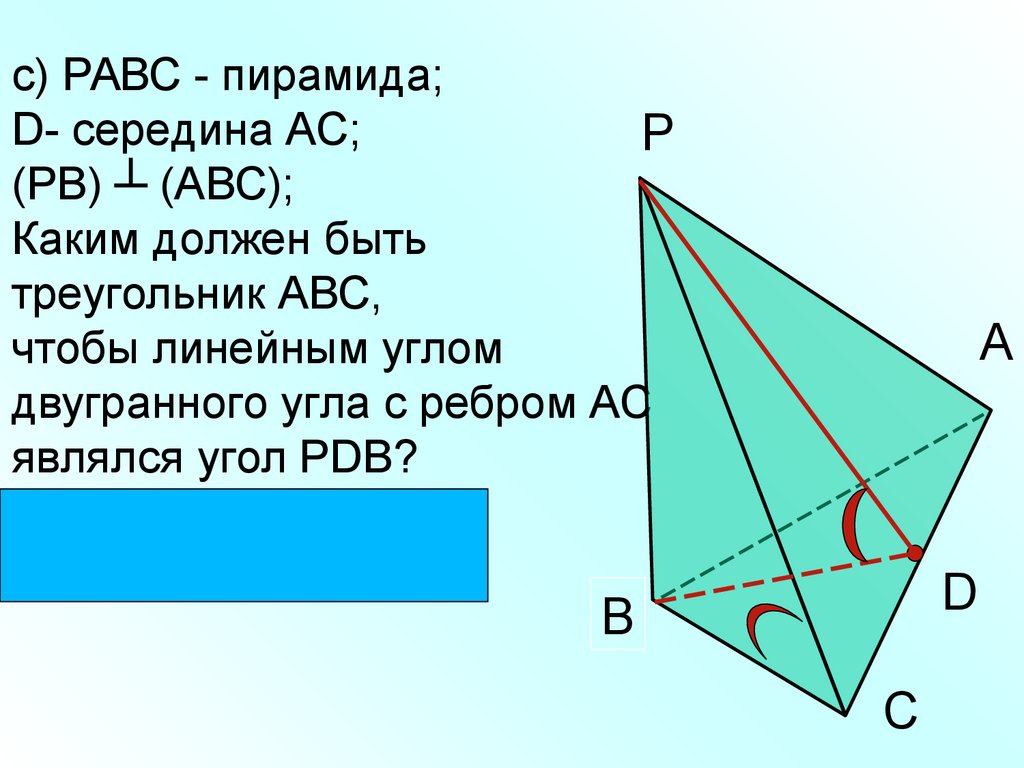
с) РАВС - пирамида;D- середина АС;
Р
(РВ) ┴ (АВС);
Каким должен быть
треугольник АВС,
чтобы линейным углом
двугранного угла с ребром АС
являлся угол РDВ?
угол РАВ?
угол РСВ?
А
D
В
С
13.
3. Задачи на построениелинейного угла для данного двугранного.
14.
а) Построить линейный уголдвугранного угла с ребром АС,
если в пирамиде РАВС:
АВ=ВС, (РВ) ┴ (АВС);
∠РАСВ - ?
15.
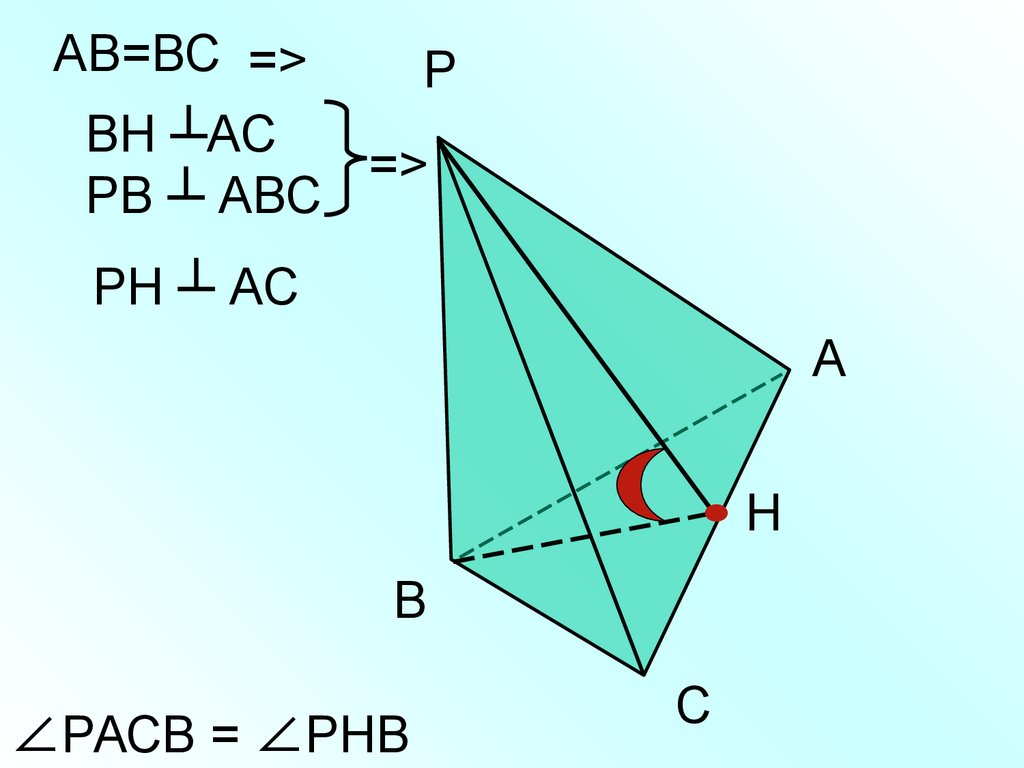
АВ=ВС =>Р
ВН ┴АС
=>
РВ ┴ АВС
РН ┴ АС
А
Н
В
∠РАСВ = ∠РНВ
С
16.
в) Построить линейный уголдвугранного угла с ребром АС,
если в пирамиде РАВС:
грань АВС – правильный треугольник,
О – точка пересечения медиан
треугольника АВС, (РО) ┴ (АВС);
∠РАСВ - ?
17.
ВК-медиана,Р
ΔАВС-правильный
=> ВК - высота
ВО ┴АС
=>
РО ┴ АВС
К
С
РК ┴ АС
А
∠РАСВ =∠РКВ
О
В
18.
с) Построить линейныйугол двугранного угла с
ребром АС, если в
пирамиде РАВС:
грань АВС –
правильный треугольник,
О – середина АВ,
(РО) ┴ (АВС);
∠РАСО - ?
19.
АВ=ВС => ВН ┴АСКО║ВН
КО ┴АС
=>
РО ┴ АВС
КР ┴ АС
А
К
Н
С
Р
О
В
∠РАСВ =∠РКО
20.
D) Дан прямоугольник АВСDи точка Р вне его плоскости.
Построить линейный угол
двугранного угла с ребром DС, если:
(РВ) ┴ (АВС);
∠ВСDР - ?
21.
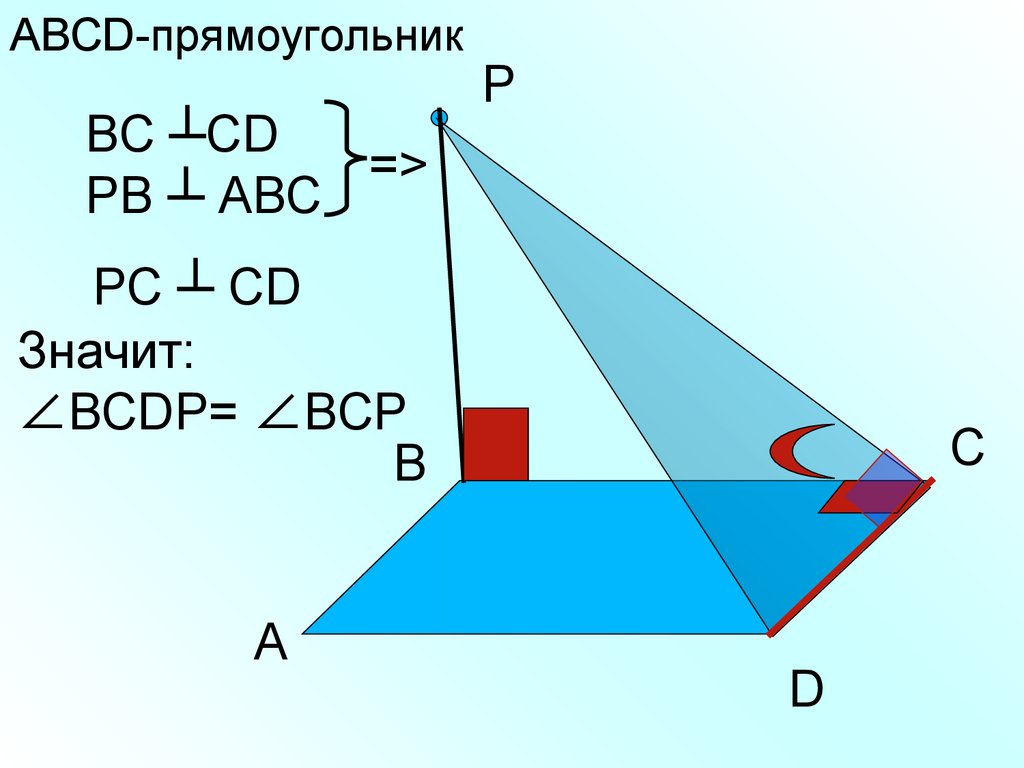
АВСD-прямоугольникВС ┴СD
=>
РВ ┴ АВС
Р
РС ┴ СD
Значит:
∠ВСDР= ∠ВСР
В
А
С
D
22.
е)Дан прямоугольник АВСDи точка Р вне его плоскости.
Построить линейный угол
двугранного угла с ребром DС, если:
(РО) ┴ (АВС).
ОͼАВ;
∠ОСDР - ?
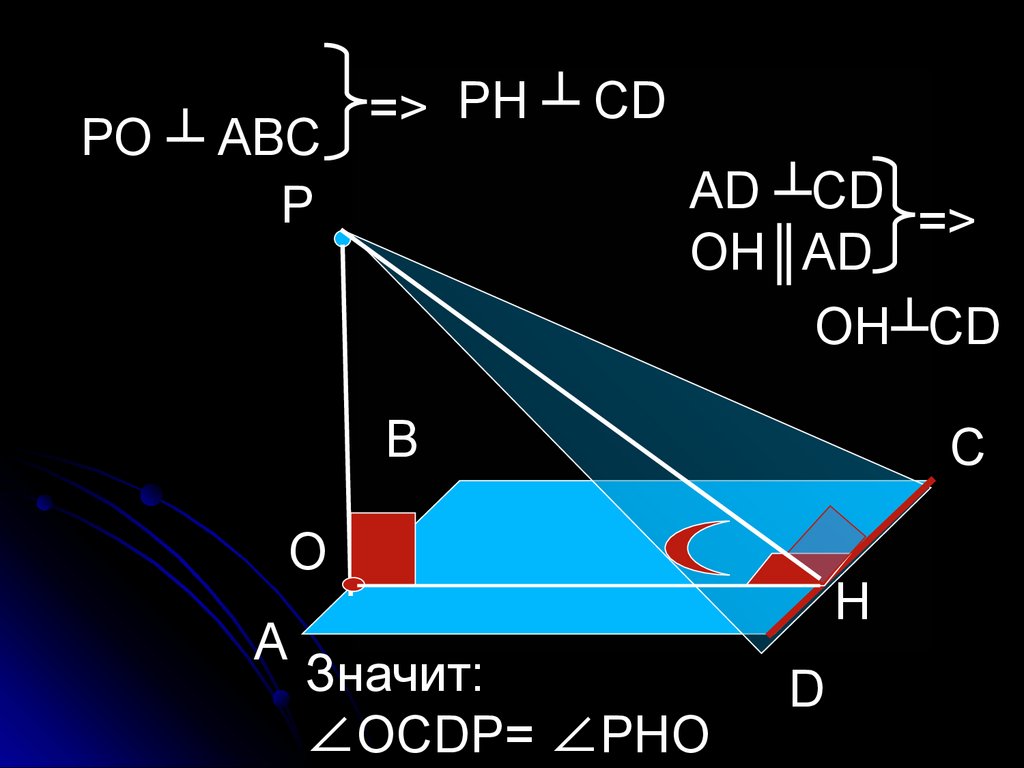
23.
РО ┴ АВСР
=> РН ┴ СD
АD ┴СD
=>
ОН║АD
ОН┴СD
В
С
О
А
Значит:
∠ОСDР= ∠РНО
Н
D
24.
f)Дан прямоугольник АВСDи точка Р вне его плоскости.
Построить линейный угол
двугранного угла с ребром DС, если:
О – точка пересечения
диагоналей АВСD,
(РО) ┴ (АВС).
∠ОСDР - ?
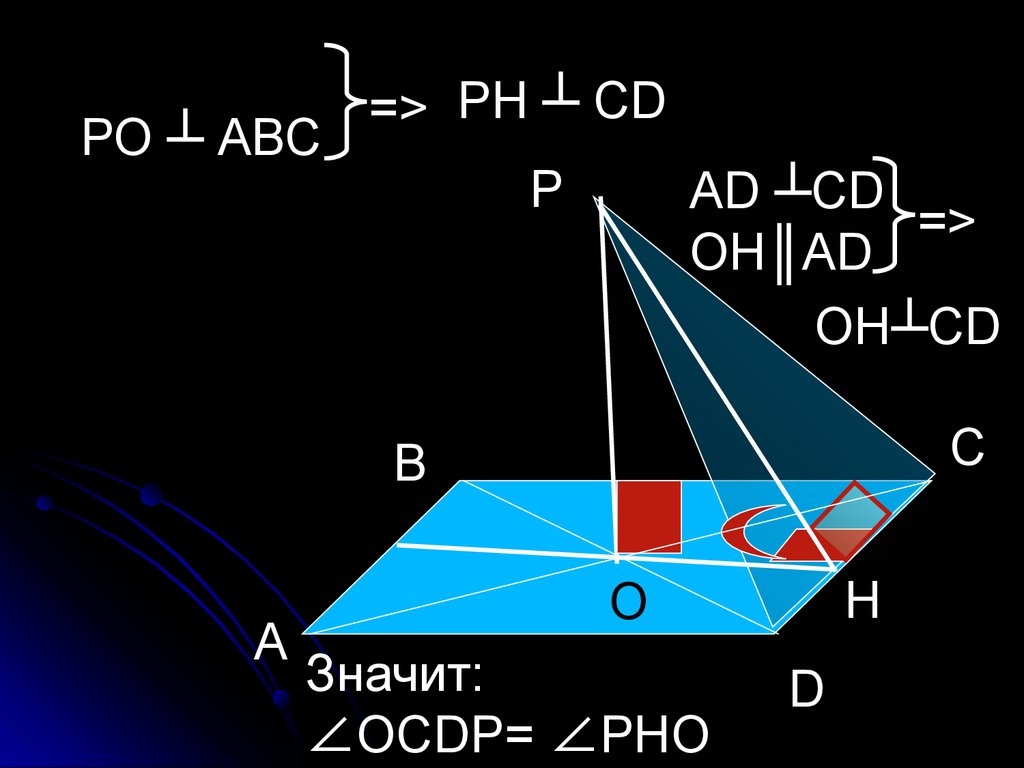
25.
РО ┴ АВС=> РН ┴ СD
Р
АD ┴СD
=>
ОН║АD
ОН┴СD
С
В
А
Н
О
Значит:
∠ОСDР= ∠РНО
D
26.
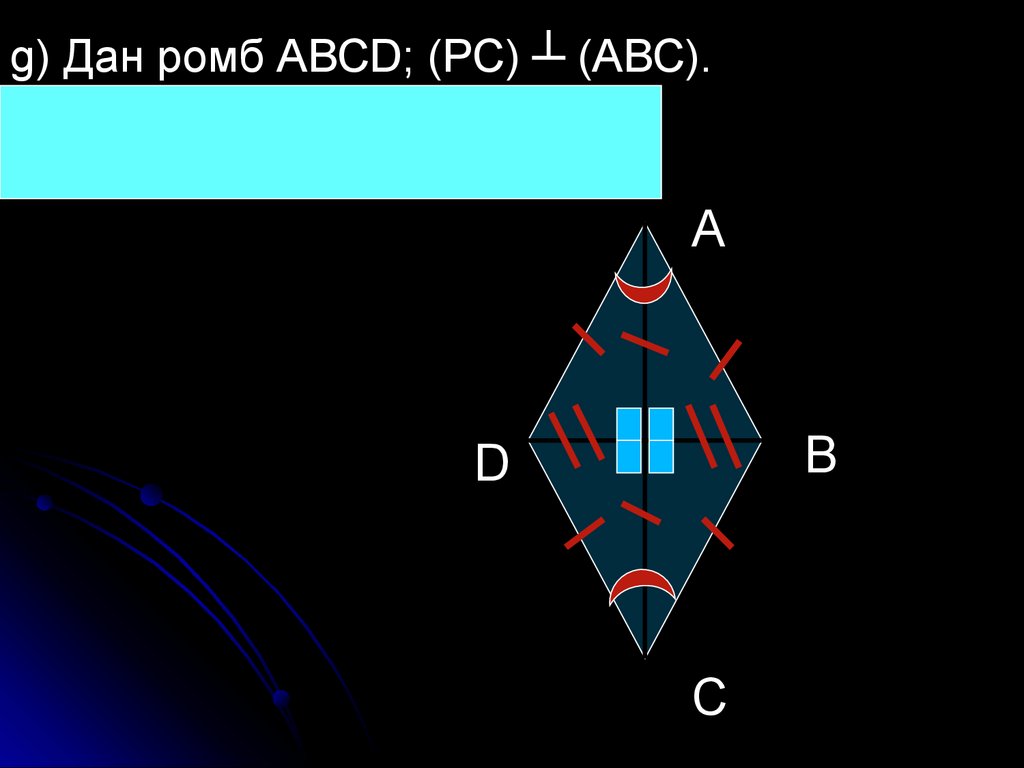
g) Дан ромб АВСD; (РС) ┴ (АВС).Построить линейный угол
двугранного угла с ребром ВD.
А
В
D
С
27.
РО ┴ ВDАВСD- ромб=>
=> СА┴ВD,
РС ┴ АВС
Р
СА∩ВD=О =>
ОС ┴ВD
С
D
О
В
Значит:
∠РВDС= ∠РОС
А
28.
i) Дана трапеция АВСD; ∠ВАD=90º;Построить линейный угол
двугранного угла с ребром АD ,
если: (РВ) ┴ (АВС).
В
А
∠ВАDР - ?
С
АD║ВС
D
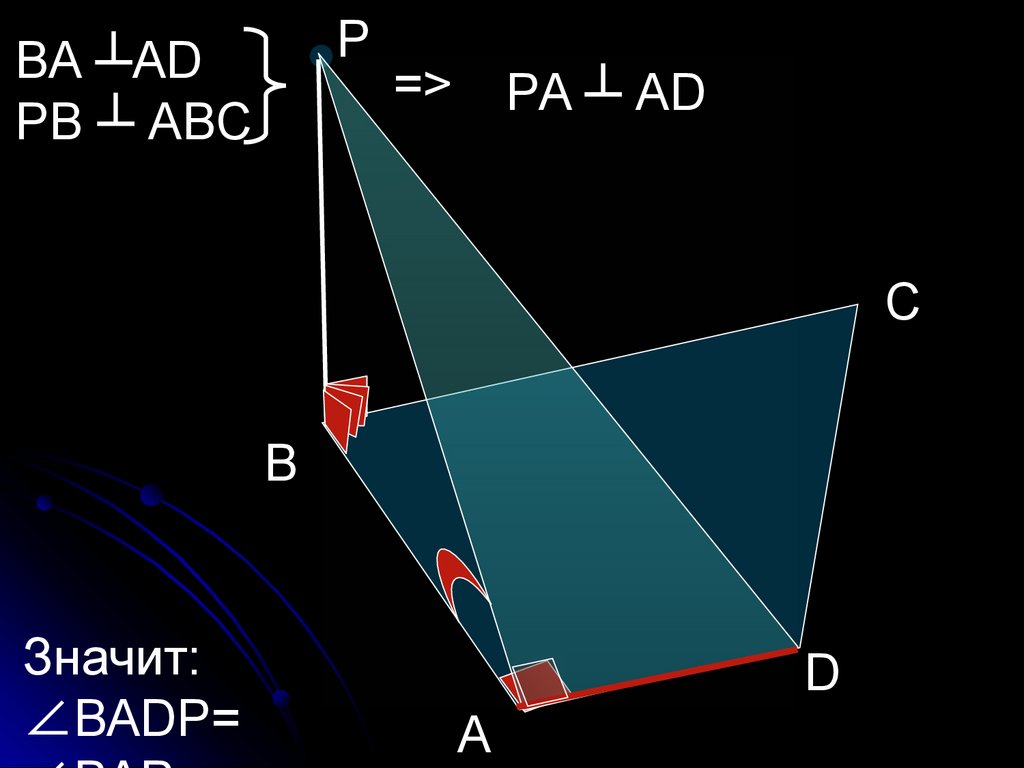
29.
РВА ┴АD
РВ ┴ АВС
=>
РА ┴ АD
С
В
Значит:
∠ВАDР=
D
А
30.
k) Dана трапеция АВСD;∠ВАD=90º;
Построить линейный угол
двугранного угла с
ребром АD , если:
О ВС; (РО) ┴ (АВС).
∠ВАDР - ?
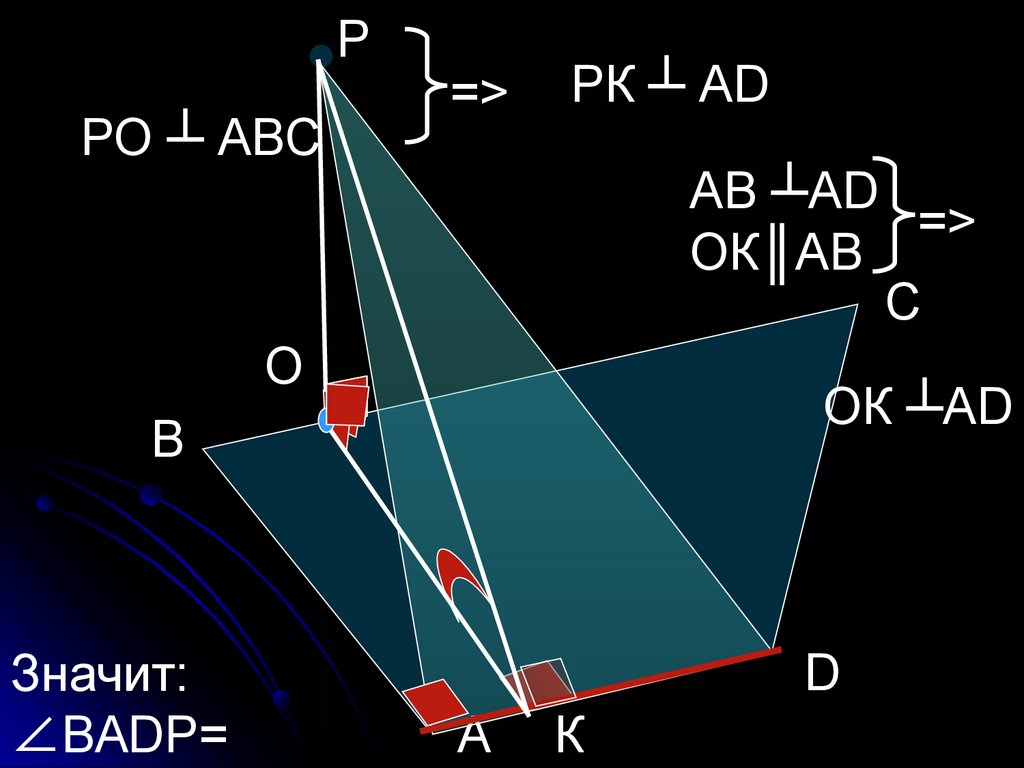
31.
РРО ┴ АВС
=>
РК ┴ АD
АВ ┴АD
=>
ОК║АВ
С
О
ОК ┴АD
В
Значит:
∠ВАDР=
D
А
К
32.
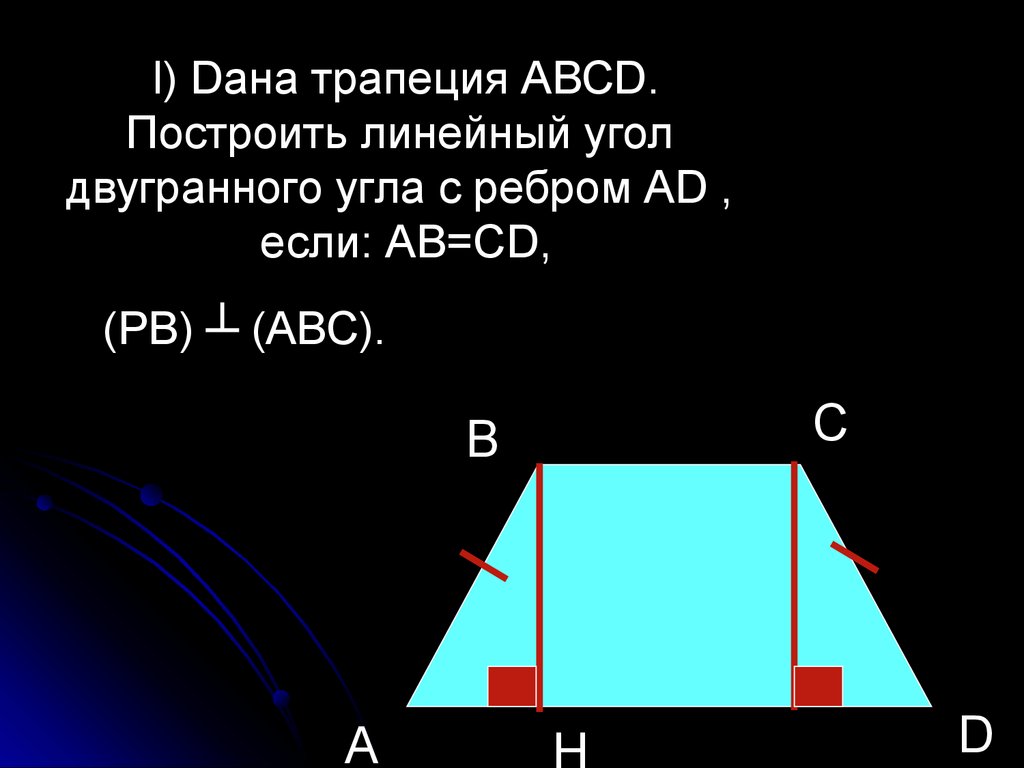
l) Dана трапеция АВСD.Построить линейный угол
двугранного угла с ребром АD ,
если: АВ=СD,
(РВ) ┴ (АВС).
В
А
С
D
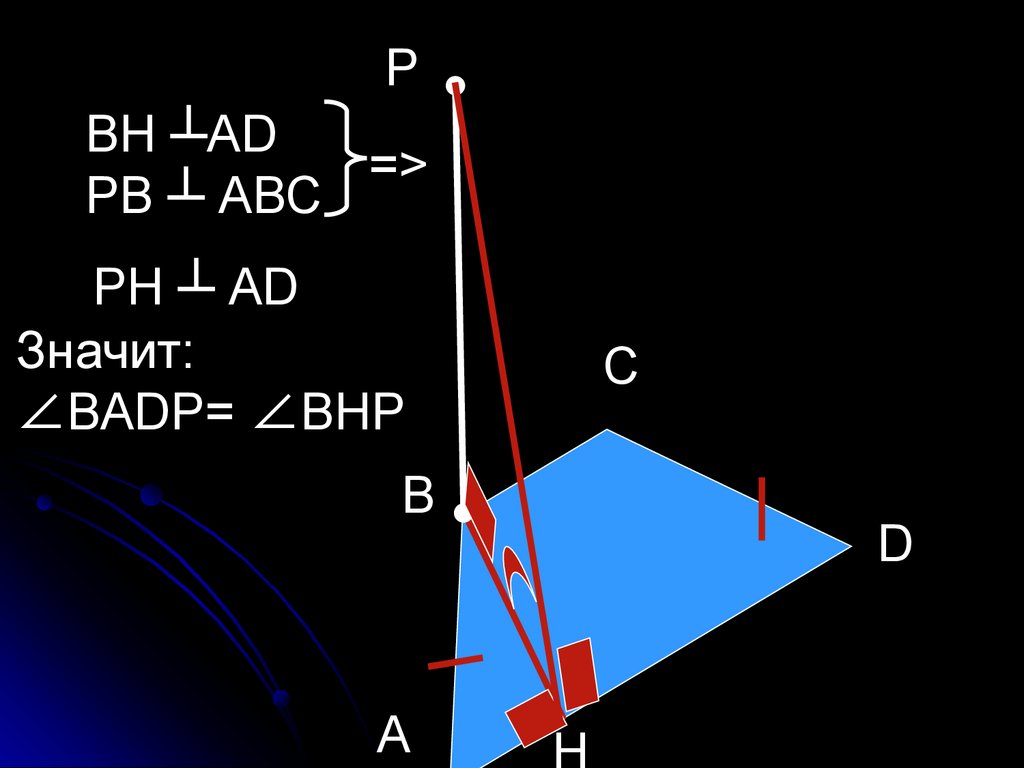
33.
РВН ┴АD
=>
РВ ┴ АВС
РН ┴ АD
Значит:
∠ВАDР= ∠ВНР
В
А
С
D
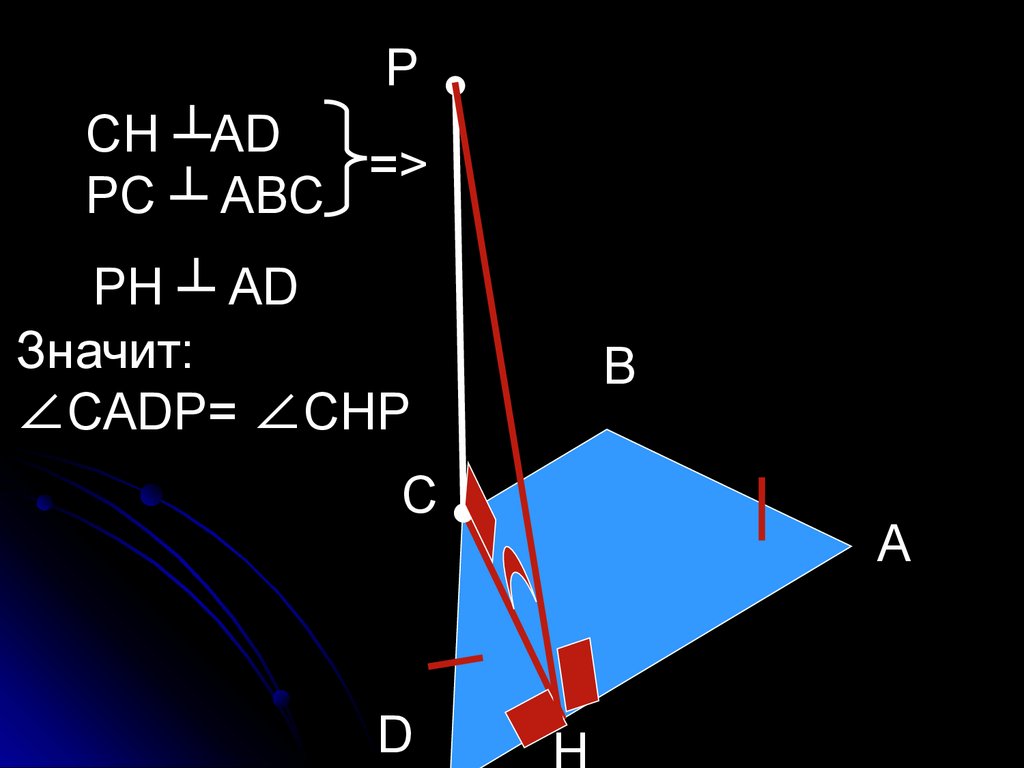
34.
m) Dана трапеция АВСD.Построить линейный угол
двугранного угла с ребром АD ,
если:
АВСD — равнобокая трапеция;
АВ=СD, (РС) ┴ (АВС);
35.
РСН ┴АD
=>
РС ┴ АВС
РН ┴ АD
Значит:
∠САDР= ∠СНР
С
D
В
А
36.
4.Вычислительные задачи.37.
а) РАВС — пирамида;найти величину двугранного угла
с ребром АС, если:
(РВ) ┴ (АВС); ∠АСВ = 90º;
ВС = РВ = 4
38.
1)АС ┴ВС
=>
РВ ┴ АВС
Р
Значит:
∠ВАСР= ∠ВСР
РС ┴ АС
А
В
С
39.
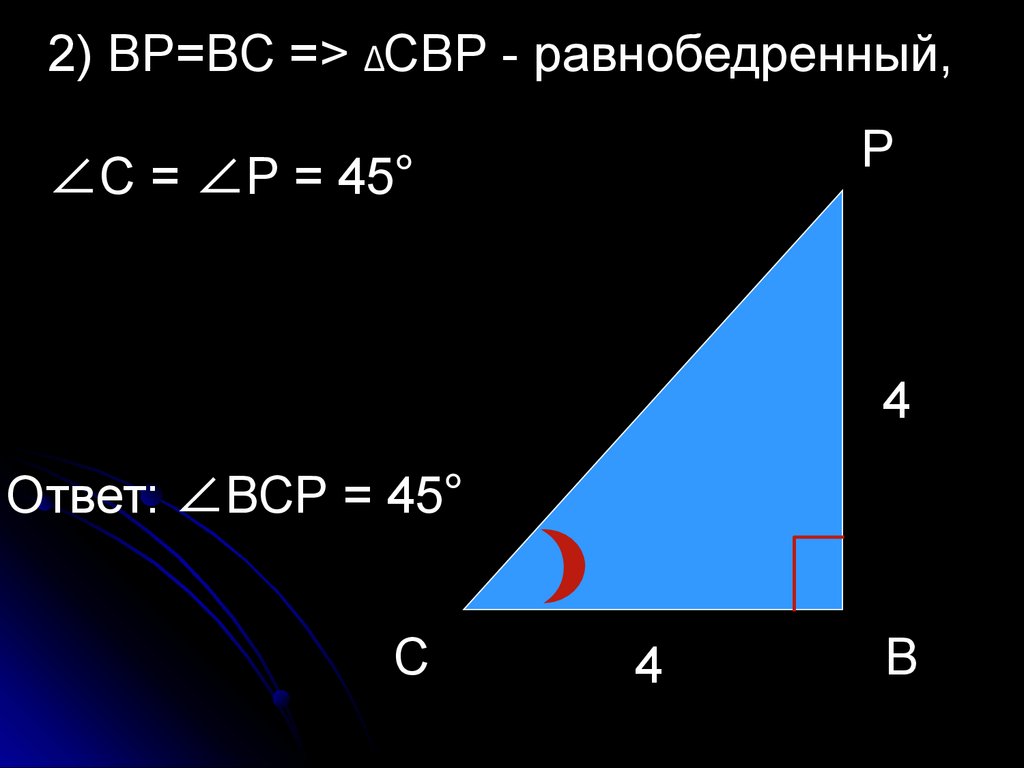
2) ВР=ВС => ΔСВР - равнобедренный,∠С = ∠Р = 45°
Р
4
Ответ: ∠ВСР = 45°
С
4
В
40.
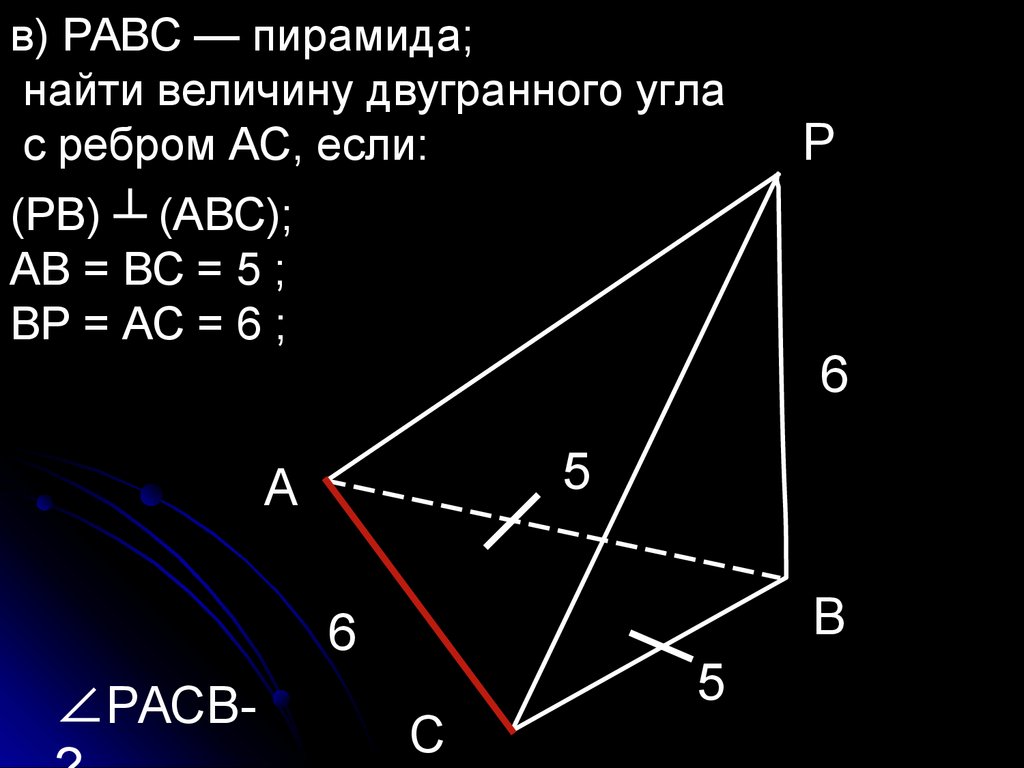
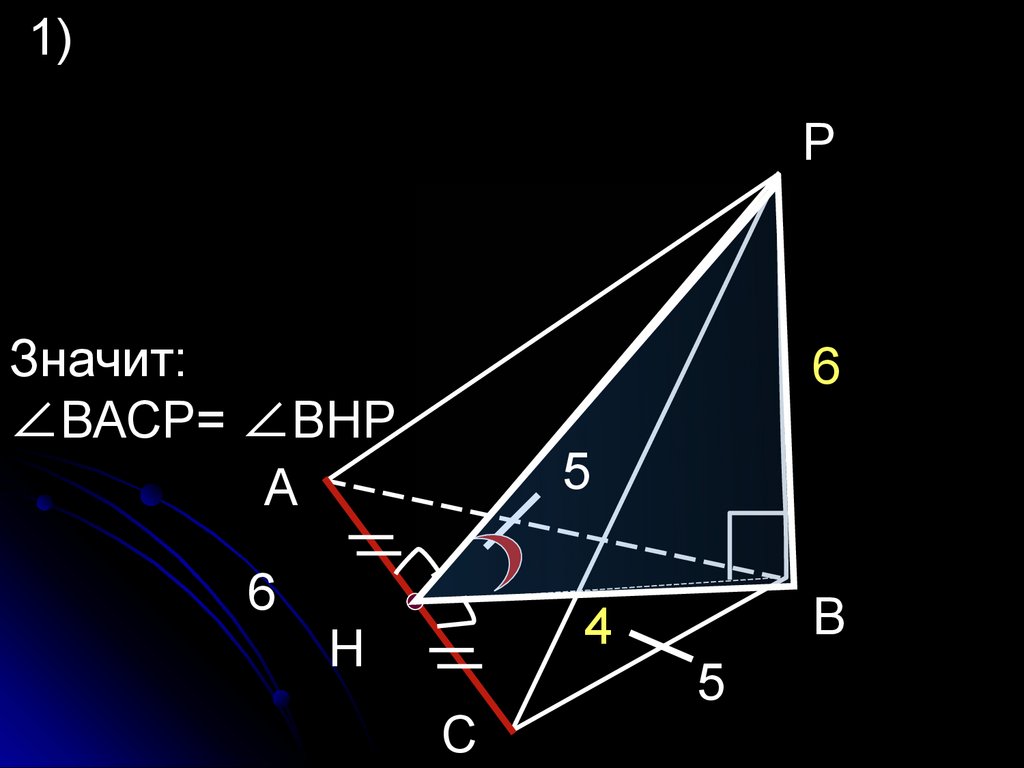
в) РАВС — пирамида;найти величину двугранного угла
с ребром АС, если:
(РВ) ┴ (АВС);
АВ = ВС = 5 ;
ВР = АС = 6 ;
6
5
А
∠РАСВ-
Р
В
6
С
5
41.
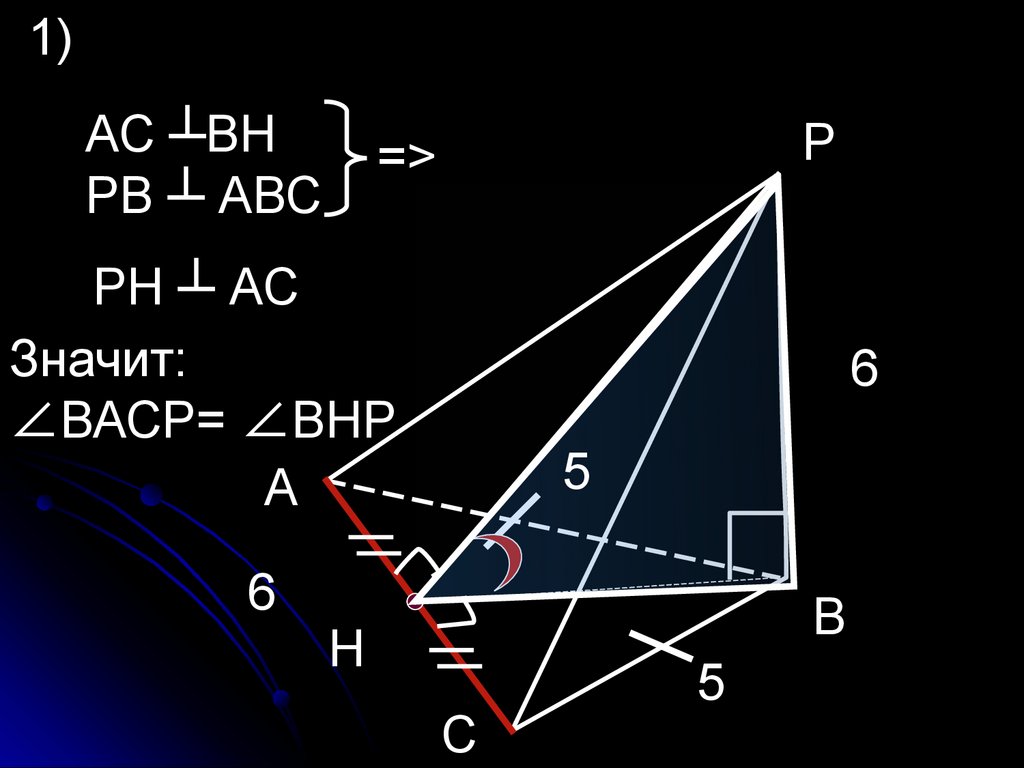
1)АС ┴ВН
РВ ┴ АВС
Р
=>
РН ┴ АС
Значит:
∠ВАСР= ∠ВНР
А
6
6
5
6
В
Н
С
5
42.
2)ΔАВС -равнобедренный,
ВН - высота,
значит: ВН- медиана,
АН=НС=3,
5
ΔВНС - прямоугольный,
ВН2=ВС2-НС2,
ВН=4
А
3
В
5
Н
3
6
С
43.
1)Р
Значит:
∠ВАСР= ∠ВНР
А
6
6
5
4
Н
С
6
В
5
44.
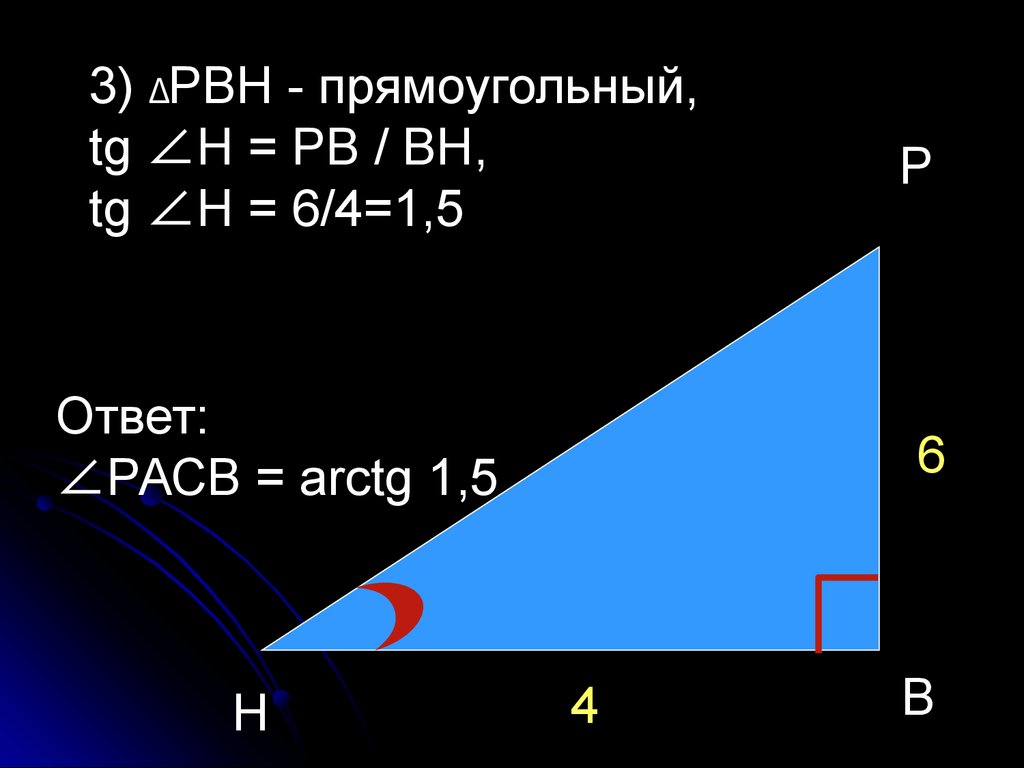
3) ΔРВН - прямоугольный,tg ∠Н = РВ / ВН,
tg ∠Н = 6/4=1,5
Ответ:
∠РАСВ = arctg 1,5
Н
Р
6
4
В
45.
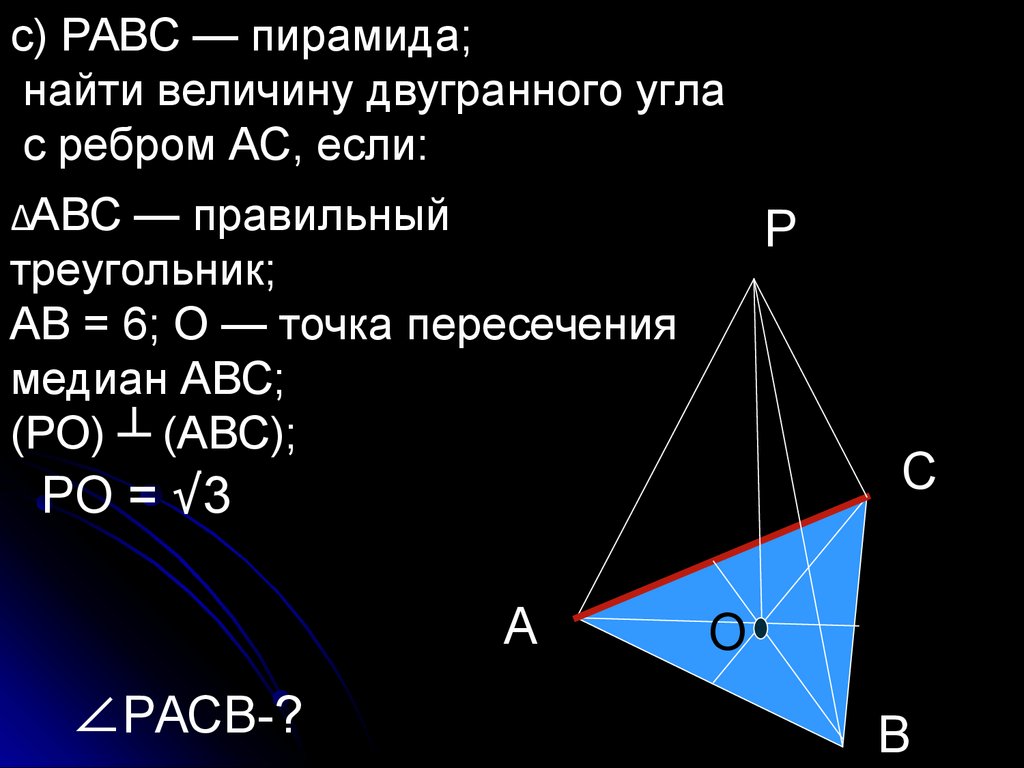
с) РАВС — пирамида;найти величину двугранного угла
с ребром АС, если:
ΔАВС
— правильный
треугольник;
АВ = 6; О — точка пересечения
медиан АВС;
(РО) ┴ (АВС);
Р
С
РО = √3
∠РАСВ-?
А
О
В
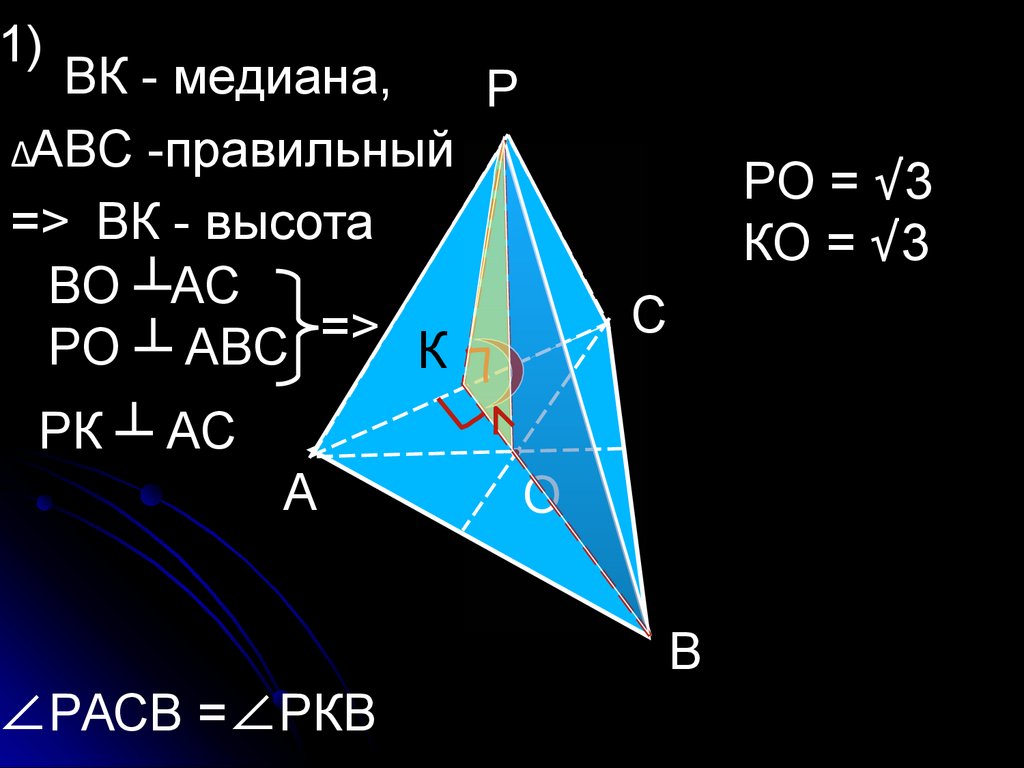
46.
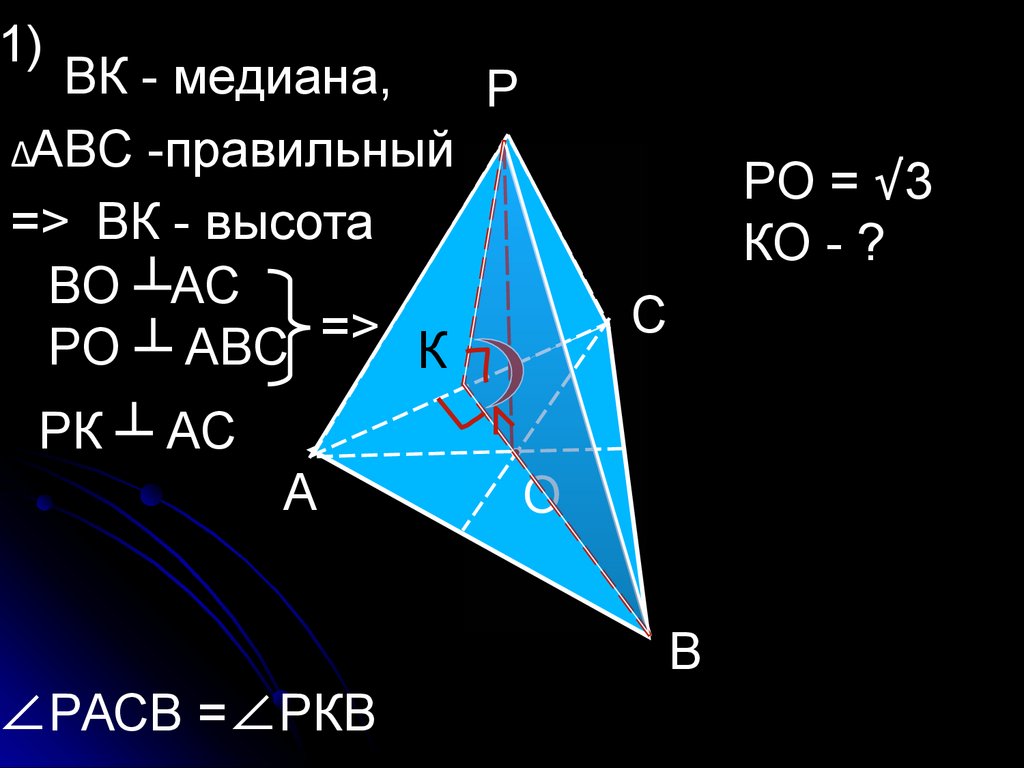
1)ВК - медиана,
Р
ΔАВС -правильный
=> ВК - высота
ВО ┴АС
=>
РО ┴ АВС
К
РО = √3
КО - ?
С
РК ┴ АС
А
∠РАСВ =∠РКВ
О
В
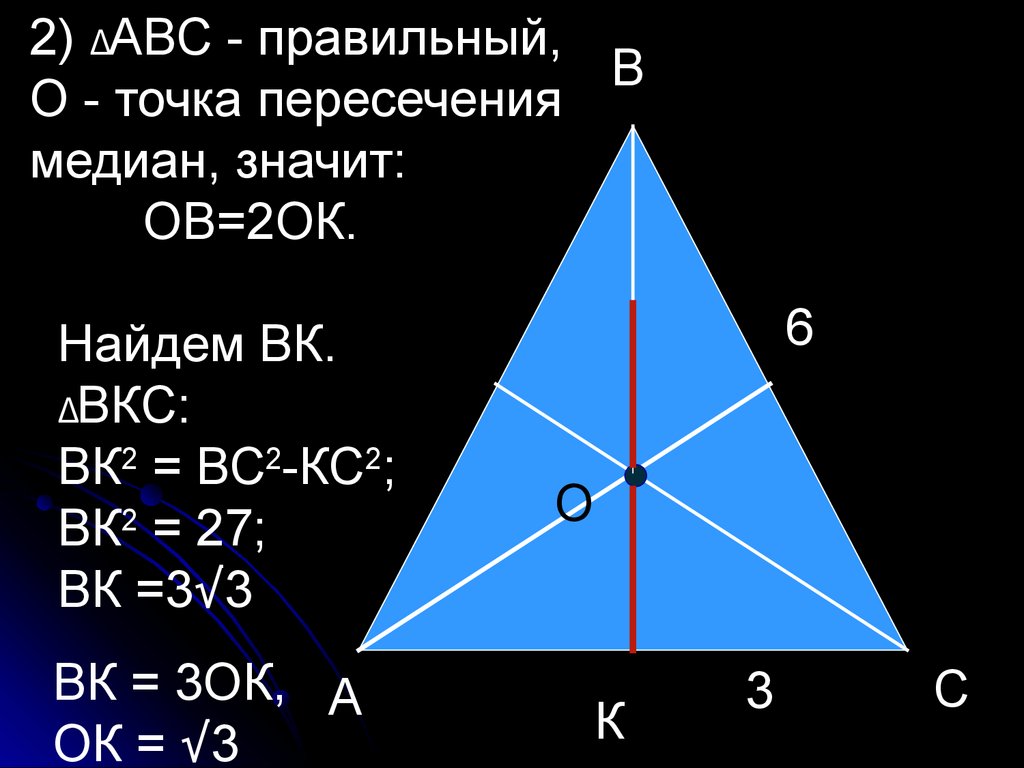
47.
2) ΔАВС - правильный,В
О - точка пересечения
медиан, значит:
ОВ=2ОК.
Найдем ВК.
ΔВКС:
ВК2 = ВС2-КС2;
ВК2 = 27;
ВК =3√3
ВК = 3ОК, А
ОК = √3
6
О
К
3
С
48.
1)ВК - медиана,
Р
ΔАВС -правильный
=> ВК - высота
ВО ┴АС
=>
РО ┴ АВС
К
РО = √3
КО = √3
С
РК ┴ АС
А
∠РАСВ =∠РКВ
О
В
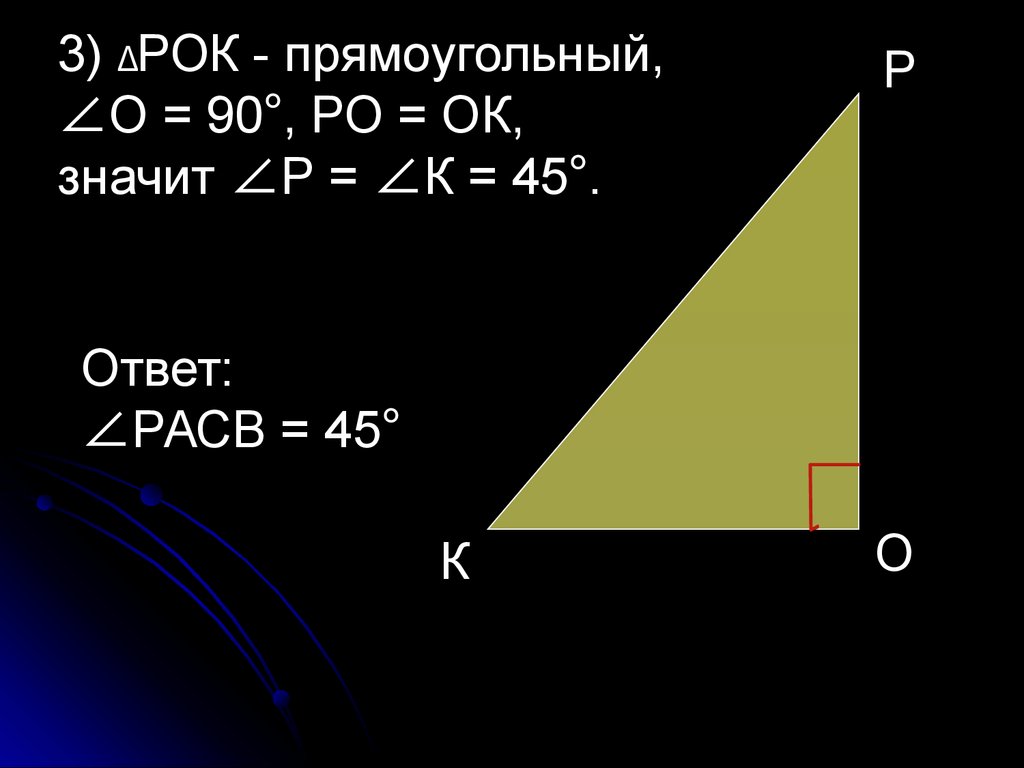
49.
3) ΔРОК - прямоугольный,∠О = 90°, РО = ОК,
значит ∠Р = ∠К = 45°.
Р
Ответ:
∠РАСВ = 45°
К
О
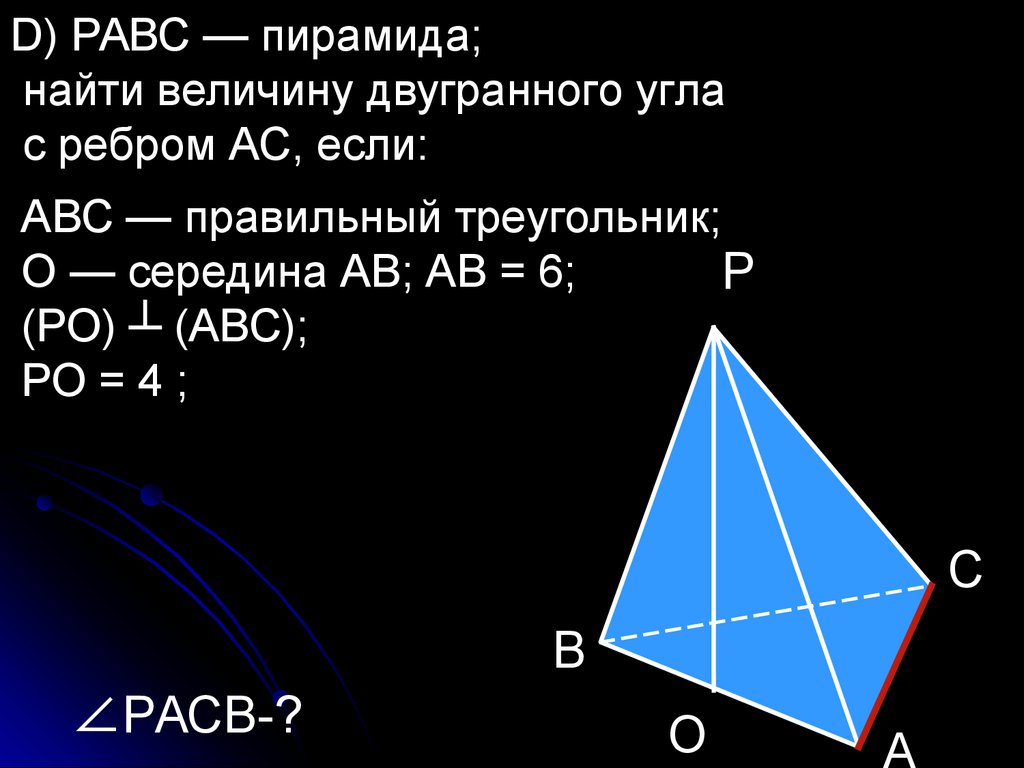
50.
D) РАВС — пирамида;найти величину двугранного угла
с ребром АС, если:
АВС — правильный треугольник;
О — середина АВ; АВ = 6;
Р
(РО) ┴ (АВС);
РО = 4 ;
С
∠РАСВ-?
В
О
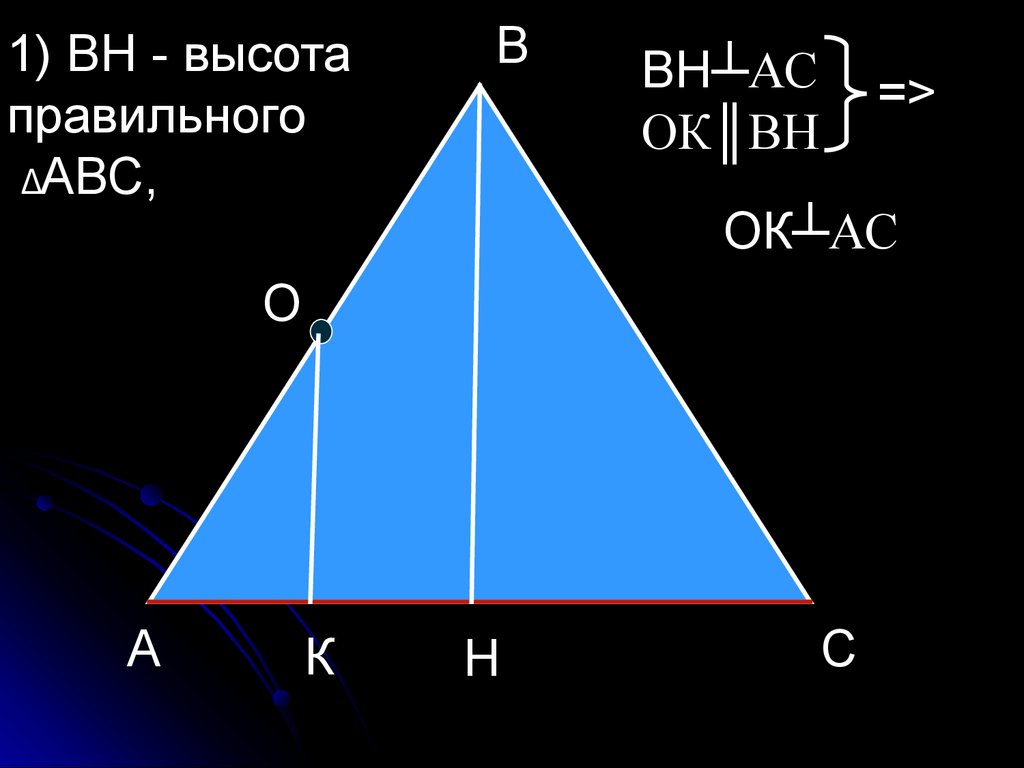
51.
1) ВН - высотаправильного
ΔАВС,
В
ВН┴АС
ОК║ВН
=>
ОК┴АС
О
А
К
Н
С
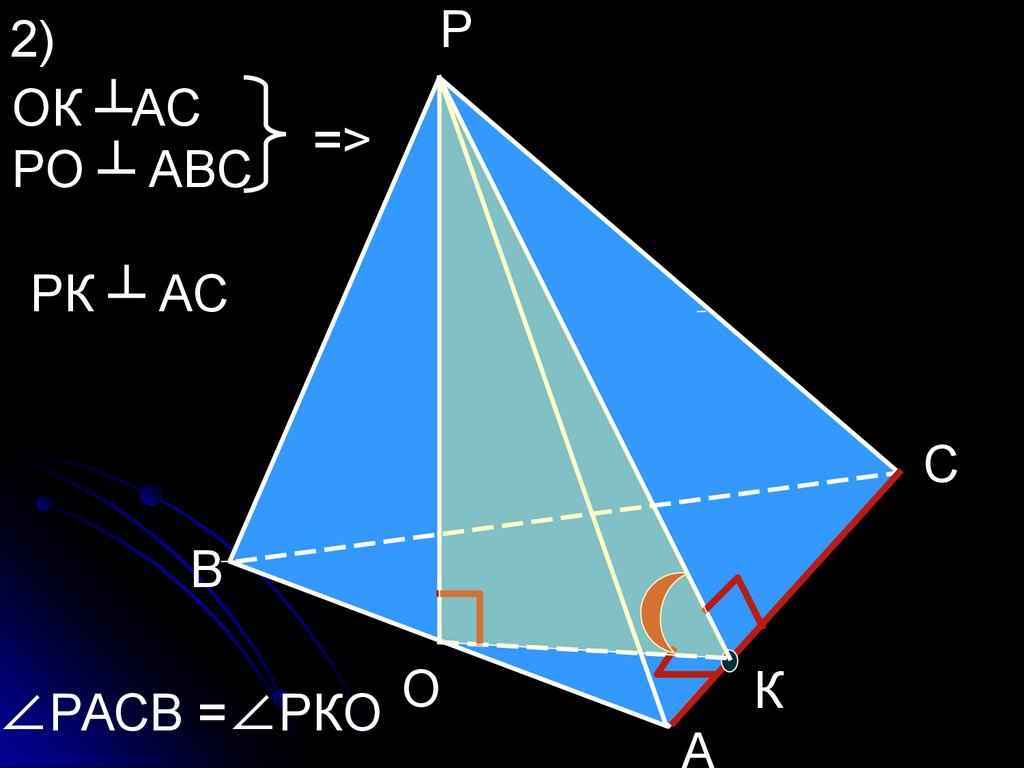
52.
2)ОК ┴АС
РО ┴ АВС
Р
=>
РК ┴ АС
С
В
О
∠РАСВ =∠РКО
К
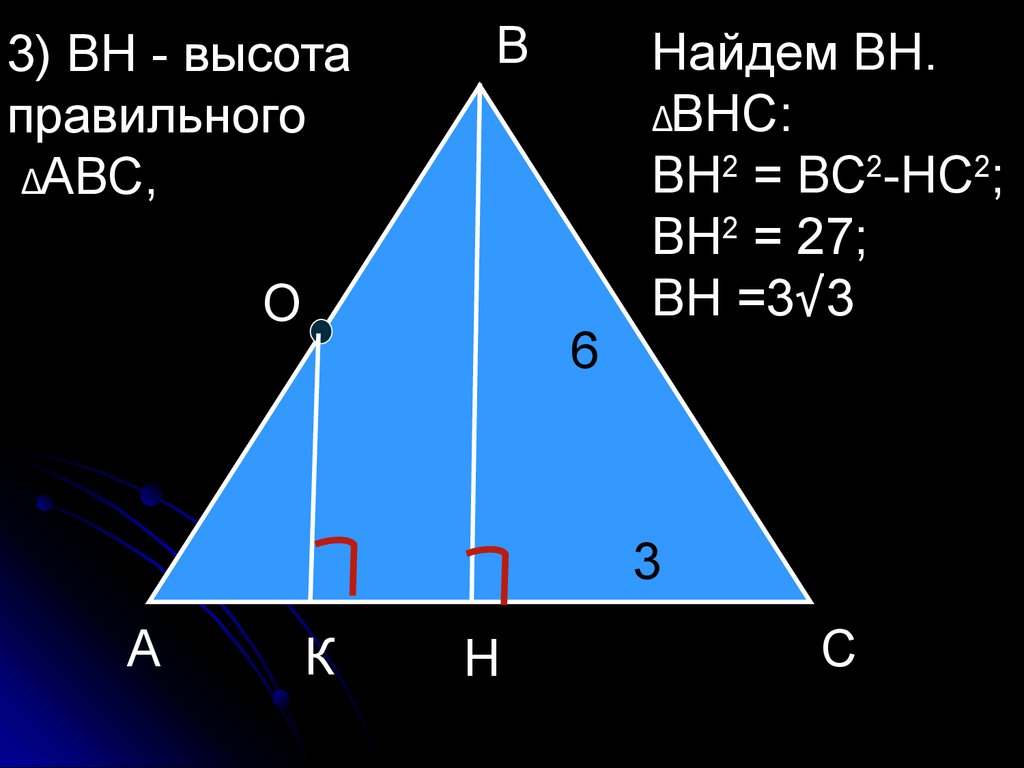
53.
3) ВН - высотаправильного
ΔАВС,
В
О
6
Найдем ВН.
ΔВНС:
ВН2 = ВС2-НС2;
ВН2 = 27;
ВН =3√3
3
А
К
Н
С
54.
ВВН =3√3
ΔАВН, О - середина АВ,
ОК║ВН => ОК -средняя линия,
ОК=ВН/2
О
6
3 3
ОК=
2
А
К
Н
С
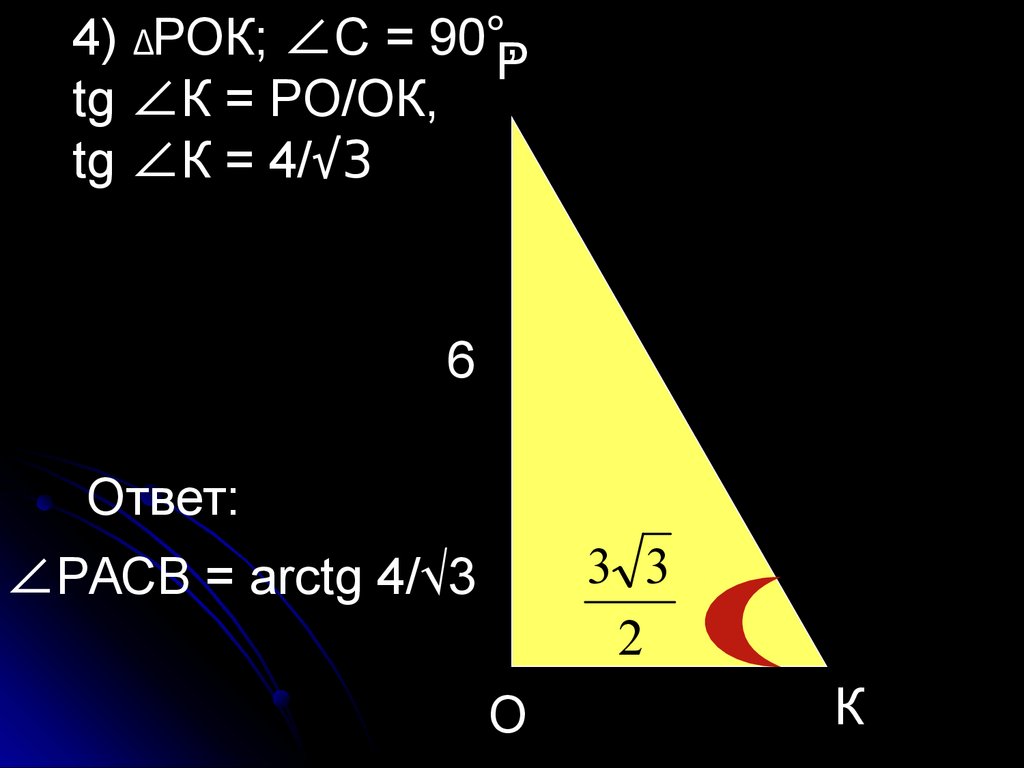
55.
4) ΔРОК; ∠С = 90°,Рtg ∠К = РО/ОК,
tg ∠К = 4/√3
6
Ответ:
∠РАСВ = arctg 4/√3
3 3
2
О
К
56.
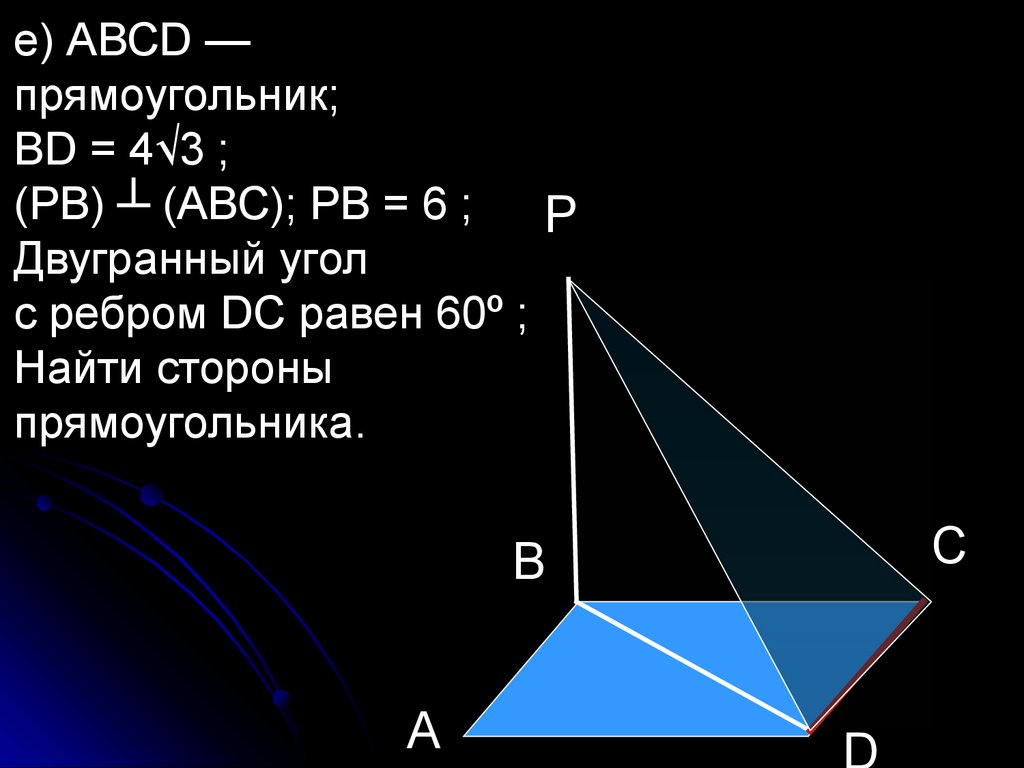
е) АВСD —прямоугольник;
ВD = 4√3 ;
(РВ) ┴ (АВС); РВ = 6 ;
Р
Двугранный угол
с ребром DС равен 60º ;
Найти стороны
прямоугольника.
В
А
С
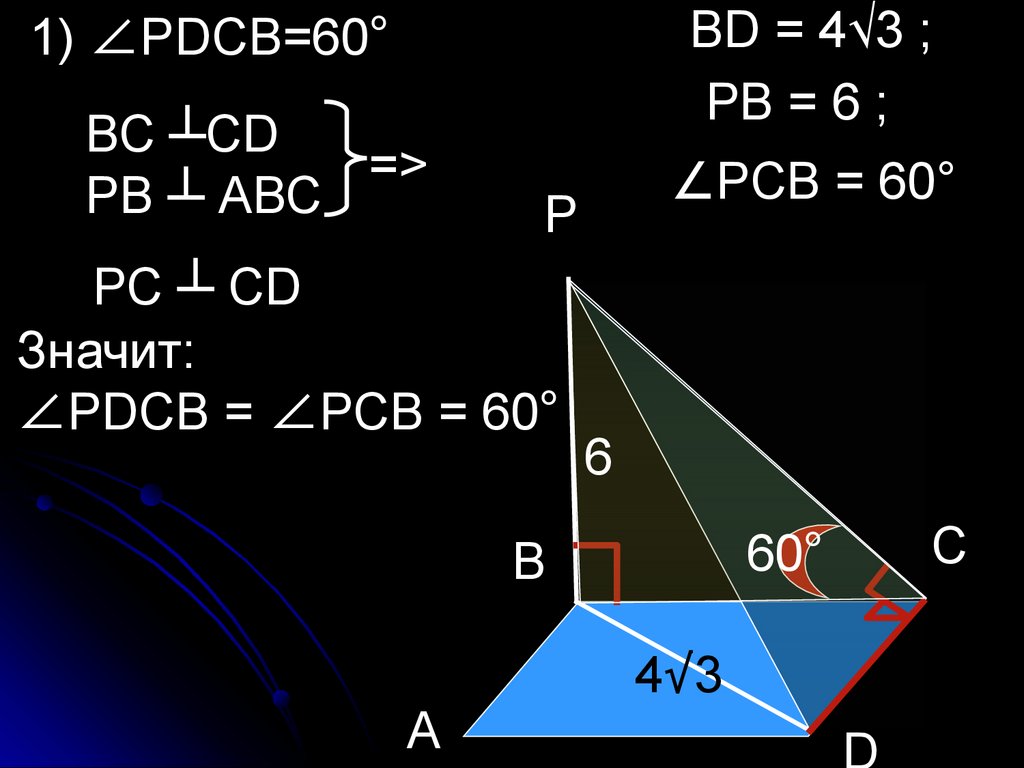
57.
1) ∠РDСВ=60°ВС ┴СD
=>
РВ ┴ АВС
ВD = 4√3 ;
РВ = 6 ;
∠РСВ = 60°
Р
РС ┴ СD
Значит:
∠РDСВ = ∠РСВ = 60°
6
60°
В
А
4√3
С
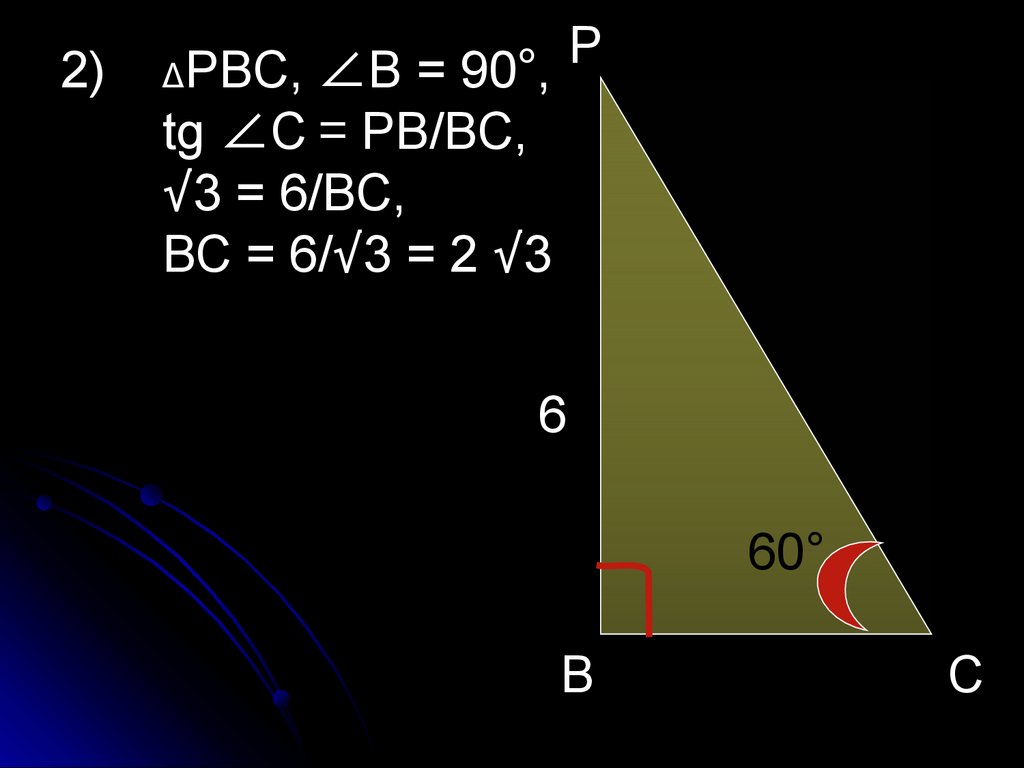
58.
2)Р
ΔРВС, ∠В = 90°,
tg ∠С = РВ/ВС,
√3 = 6/ВС,
ВС = 6/√3 = 2 √3
6
60°
В
С
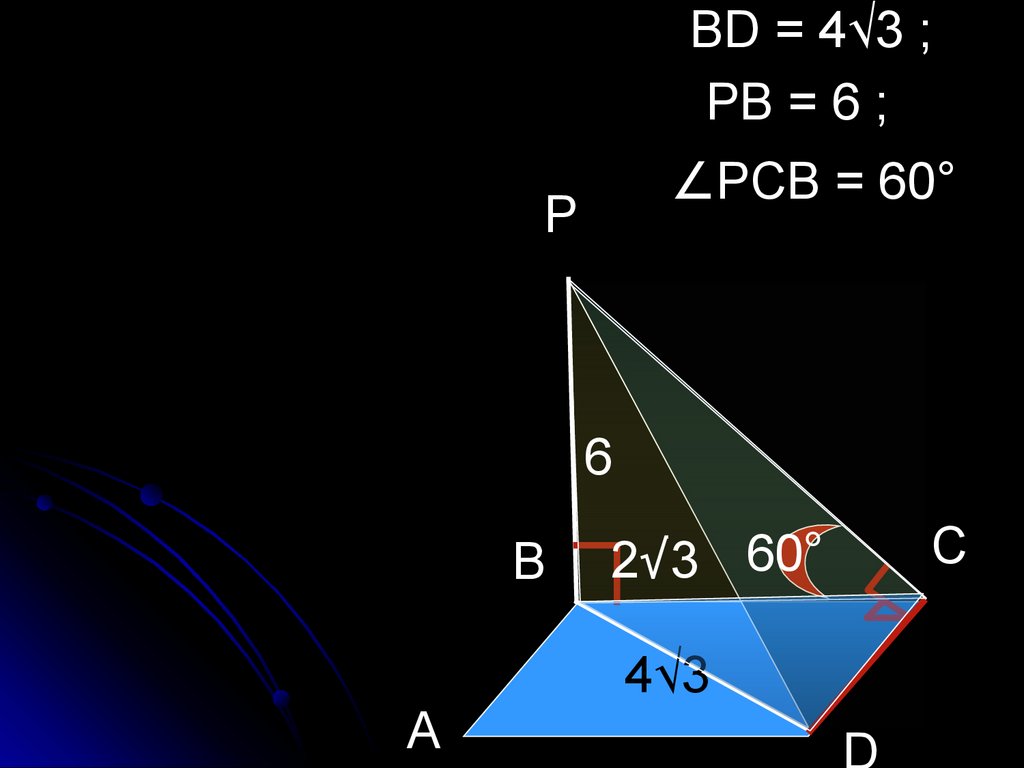
59.
ВD = 4√3 ;РВ = 6 ;
∠РСВ = 60°
Р
6
В
А
2√3 60°
4√3
С
60.
3) ΔВСD; ∠С =90°,
СD2 = ВD2 - СD2;
СD2 = 16•3-4•3;
СD2 = 36; СD = 6
В
2√3
С
4√3
Ответ: АВ = СD =6;
ВС = АD = 2√3.
D
61.
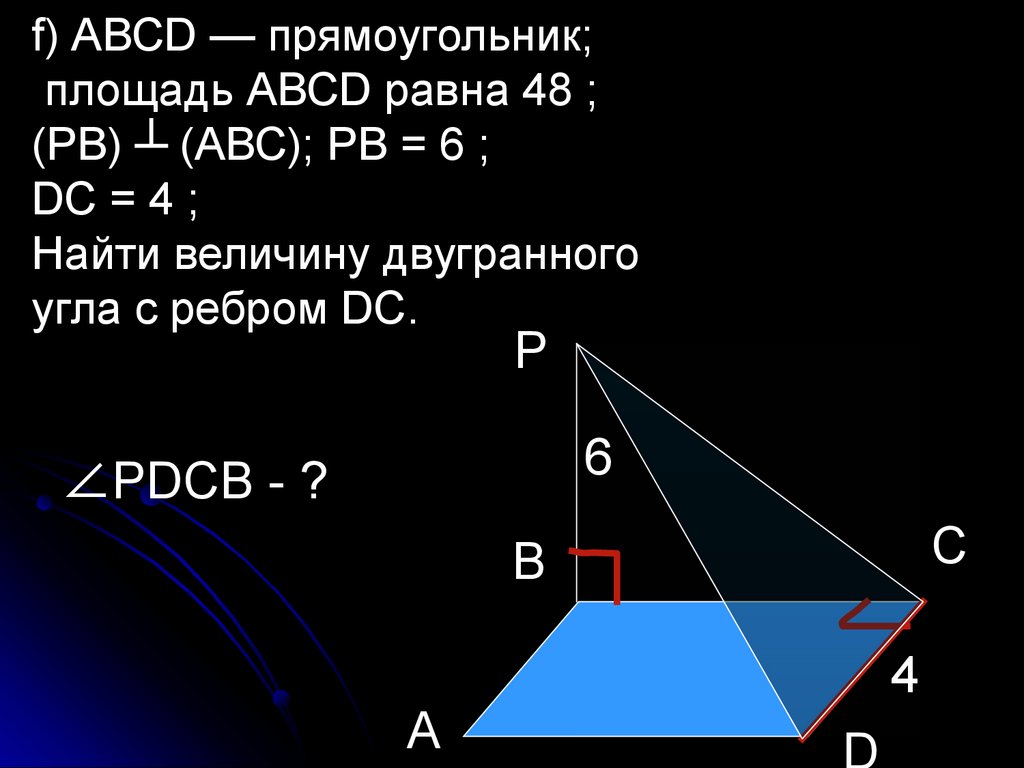
f) АВСD — прямоугольник;площадь АВСD равна 48 ;
(РВ) ┴ (АВС); РВ = 6 ;
DС = 4 ;
Найти величину двугранного
угла с ребром DС.
Р
∠РDСВ - ?
6
С
В
А
4
62.
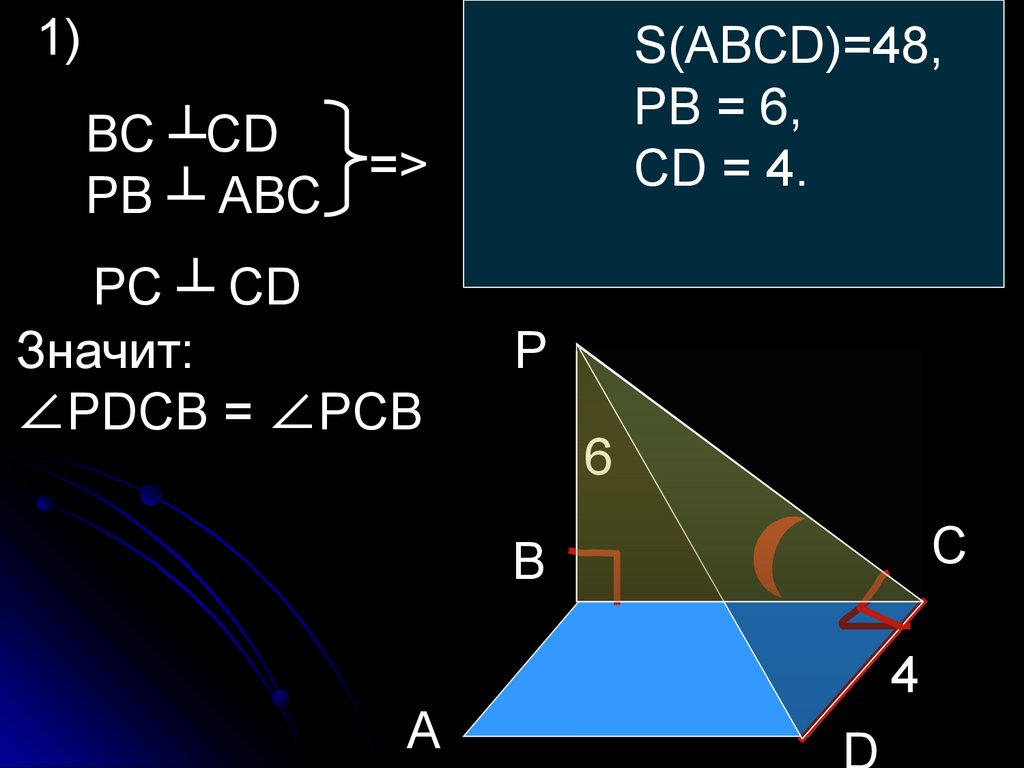
1)S(АВСD)=48,
РВ
=
6,
∠РDСВ - ?
СD = 4.
ВС ┴СD
=>
РВ ┴ АВС
РС ┴ СD
Значит:
∠РDСВ = ∠РСВ
Р
6
С
В
А
4
63.
2) АВСD - прямоугольникS(АВСD) = АВ•ВС = 48,
АВ = СD = 4,
4•ВС = 48, ВС = 12.
64.
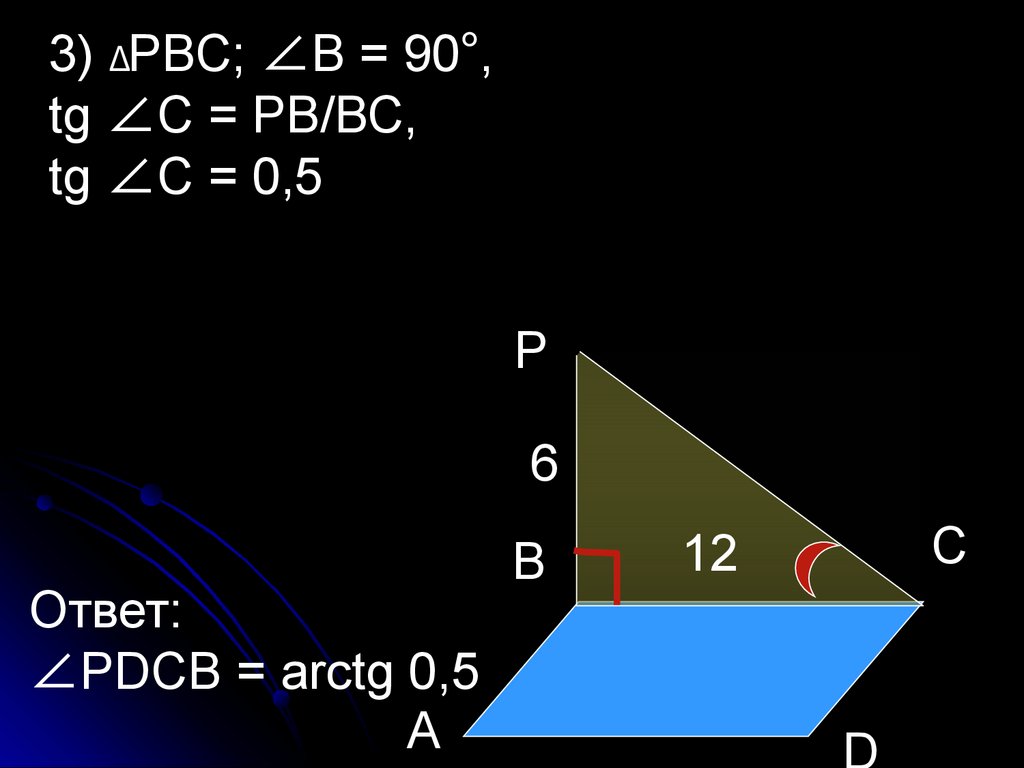
3) ΔРВС; ∠В = 90°,tg ∠С = РВ/ВС,
tg ∠С = 0,5
Р
6
Ответ:
∠РDСВ = arctg 0,5
А
В
12
С
65.
g) АВСD — ромб;ВD = 4 ;
(РС) ┴ (АВС); РС = 8 ;
Двугранный угол с
ребром ВD равен 45º ;
Найти площадь ромба.
В
a
h
d2
А
Sромба = a • h ,
Sромба =d1 • d2:2
4
d1
D
С
66.
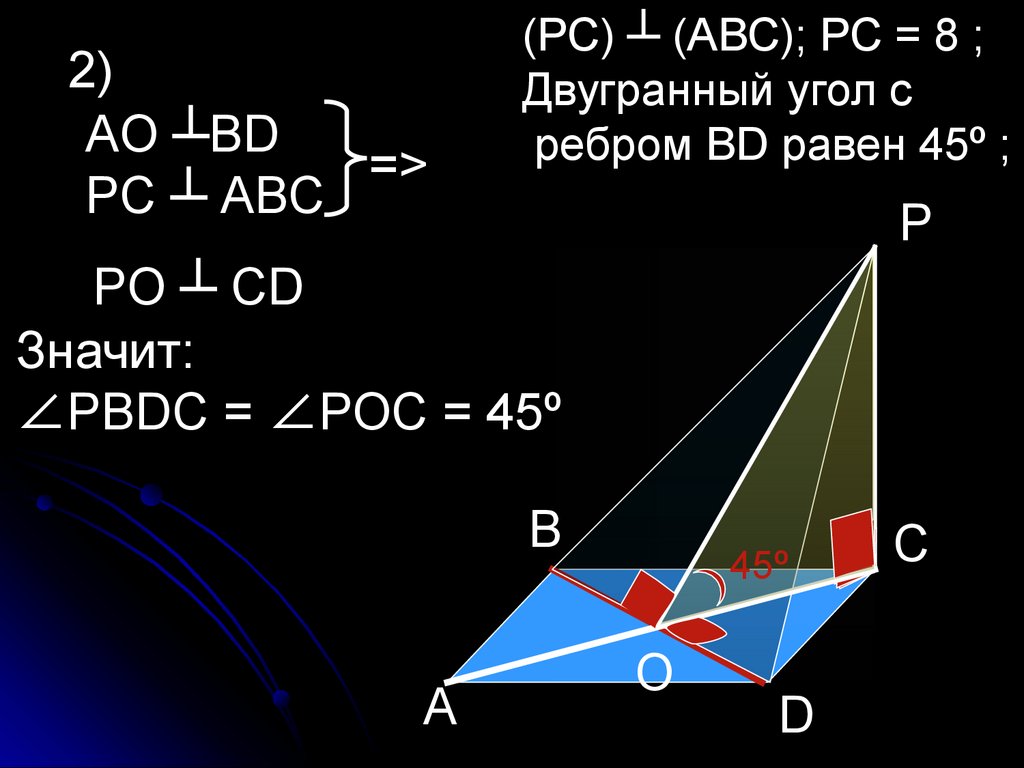
2)АО ┴ВD
=>
РС ┴ АВС
(РС) ┴ (АВС); РС = 8 ;
Двугранный угол с
ребром ВD равен 45º ;
Р
РО ┴ СD
Значит:
∠РВDС = ∠РОС = 45º
В
А
45º
О
D
С
67.
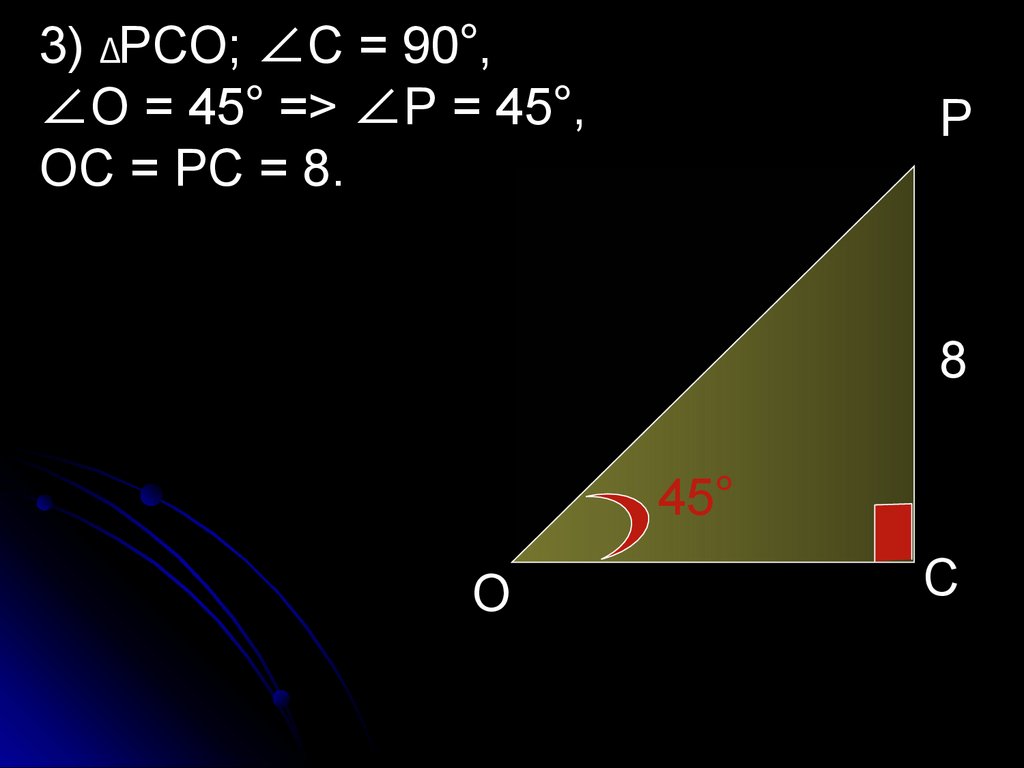
3) ΔРСО; ∠С = 90°,∠О = 45° => ∠Р = 45°,
ОС = РС = 8.
Р
8
45°
О
С
68.
В4) d1 = 2ОС = 16,
d2 = 4,
Sромба =d1 • d2:2
S = 32
d2
А
Ответ: 32
Sромба =d1 • d2:2
О
4
d1
D
С
69.
) АВСD- параллелограмм;∠АDС = 120º; АD = 8 ;
DС =6 ; (РС) ┴ (АВС);
РС = 9 ;
Найти величину двугранного
угла с ребром АD и
В
площадь АВСD .
К
С
Sпарал-ма= a • b • sin∠(a,b)
Sпарал-ма= a • h
А
8
a
120°
6
D
b
h
Н
70.
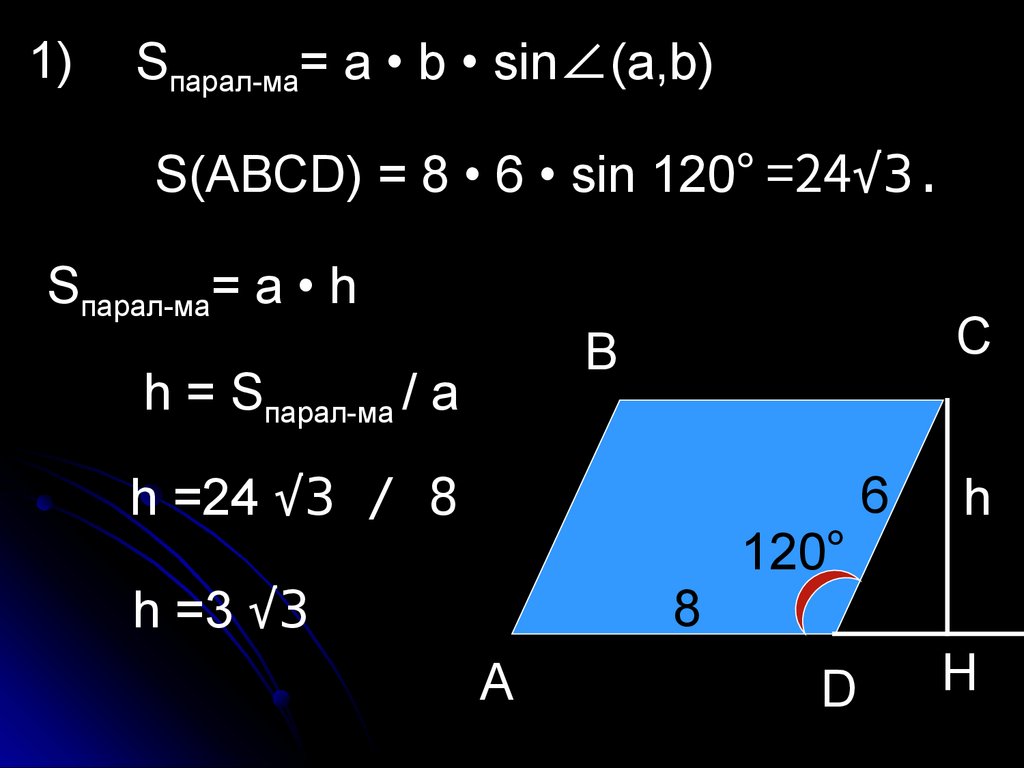
1)Sпарал-ма= a • b • sin∠(a,b)
S(АВСD) = 8 • 6 • sin 120° =24√3.
Sпарал-ма= a • h
С
В
h = Sпарал-ма / a
h =24 √3 / 8
8
h =3 √3
А
120°
D
6
h
Н
71.
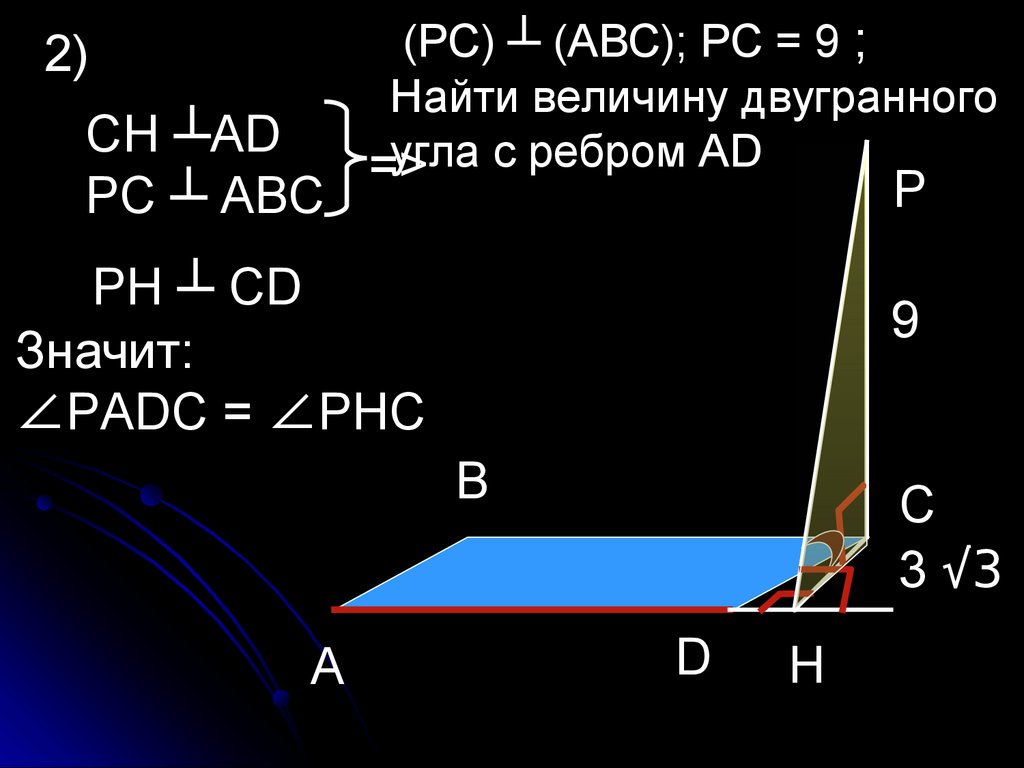
2)CH ┴AD
РС ┴ АВС
(РС) ┴ (АВС); РС = 9 ;
Найти величину двугранного
угла с ребром АD
=>
РH ┴ СD
Значит:
∠РADС = ∠РHС
A
P
9
B
C
3 √3
D
H
72.
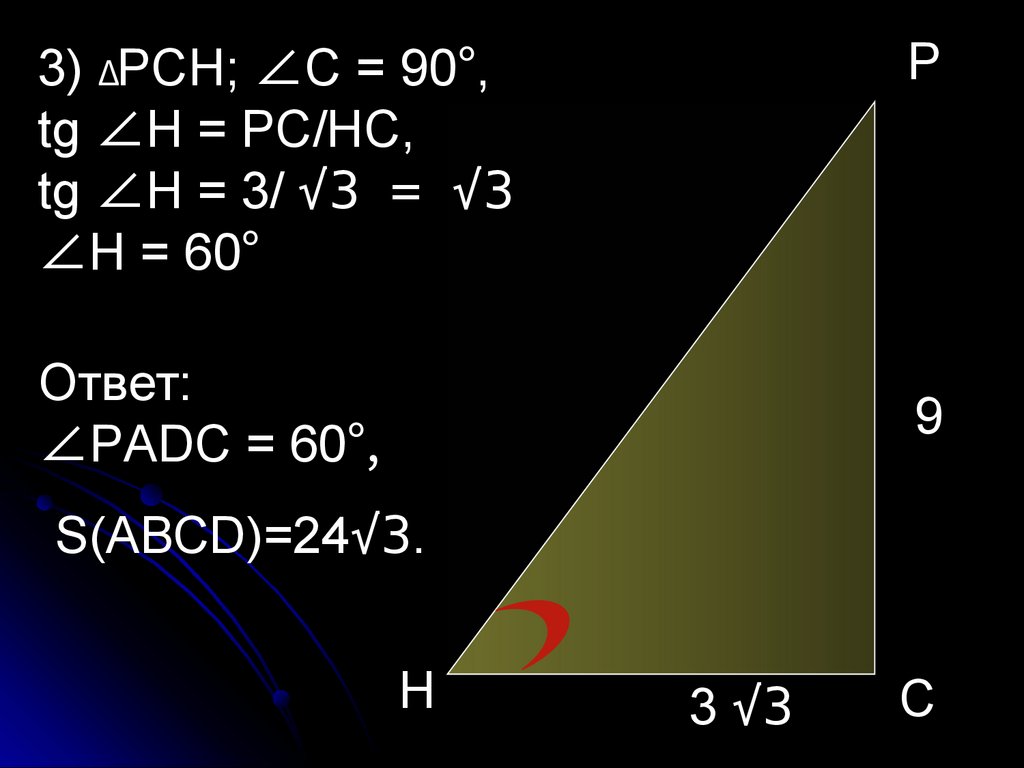
3) ΔРCH; ∠C = 90°,tg ∠H = РC/HС,
tg ∠H = 3/ √3 = √3
∠H = 60°
P
Ответ:
∠РADC = 60°,
9
S(АВСD)=24√3.
H
3 √3
C

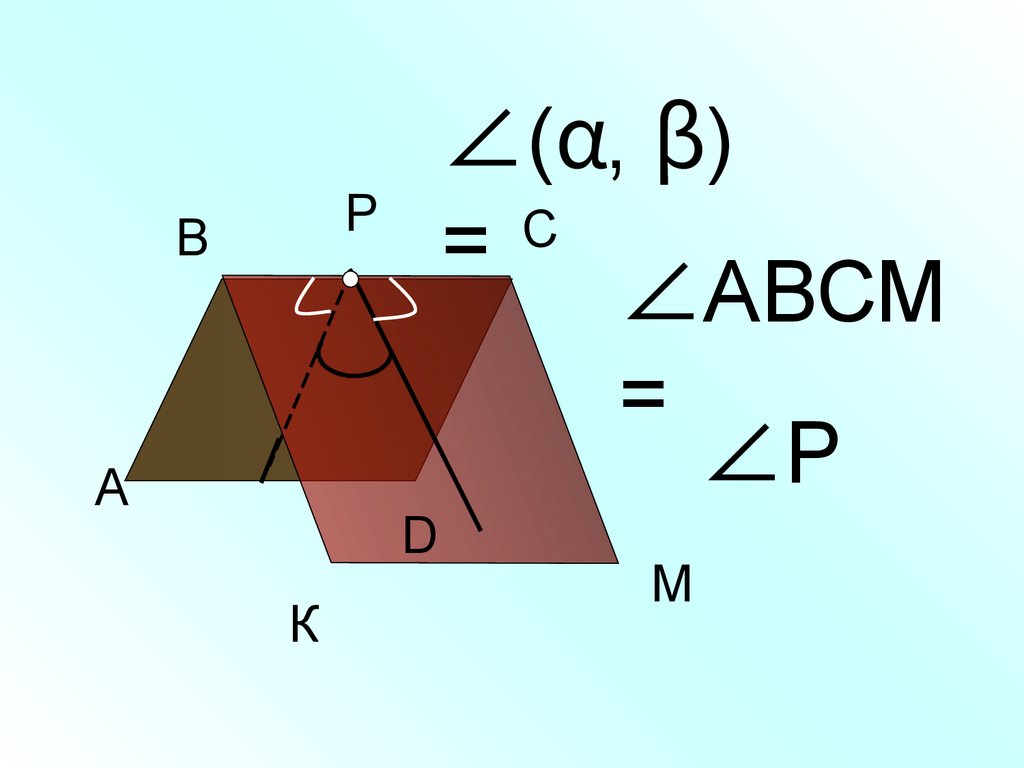























 mathematics
mathematics








