Двугранный угол

1.

2.

Повторение
a
А
Н
А
Расстояние от точки до
прямой – длина
перпендикуляра,
опущенного из точки А на
прямую.
Н
Расстояние от точки до
плоскости – длина
перпендикуляра

3.

Из точки В к плоскости проведена наклонная, равная 12 см.
Угол между наклонной и ее проекцией на плоскость равен
300. Найти расстояние от точки В до плоскости.
В
?
12 см
С
300
M

4.

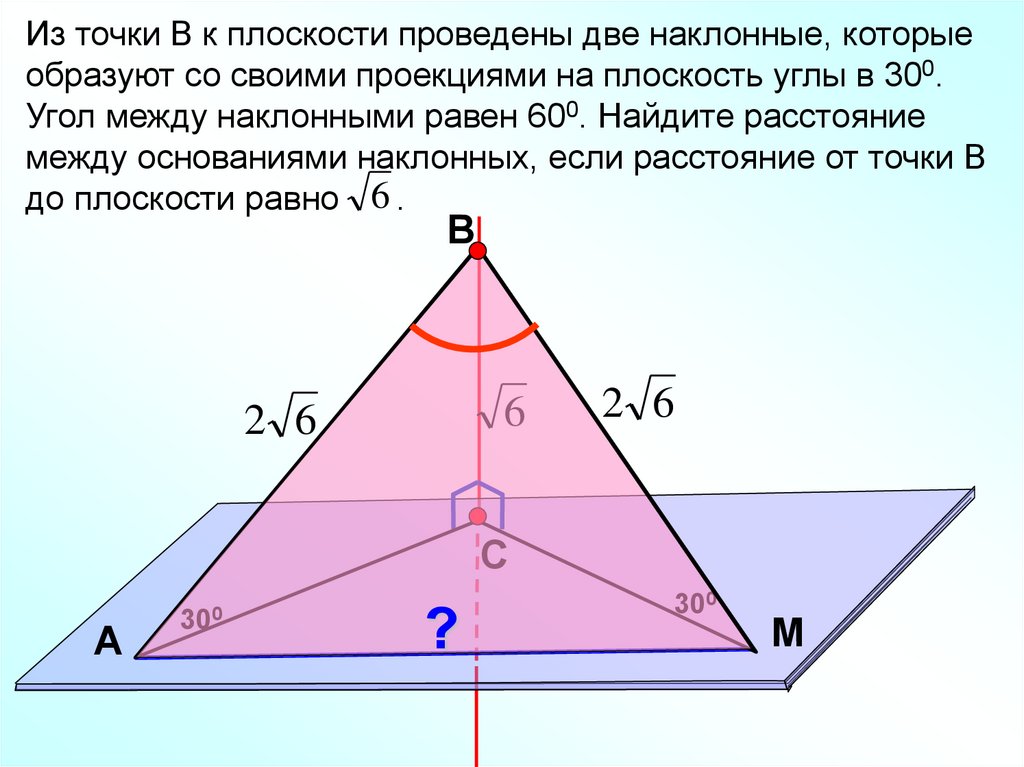
Из точки В к плоскости проведены две наклонные, которые
образуют со своими проекциями на плоскость углы в 300.
Угол между наклонными равен 600. Найдите расстояние
между основаниями наклонных, если расстояние от точки В
до плоскости равно 6 .
В
6
2 6
2 6
С
А
300
?
300
M

5.

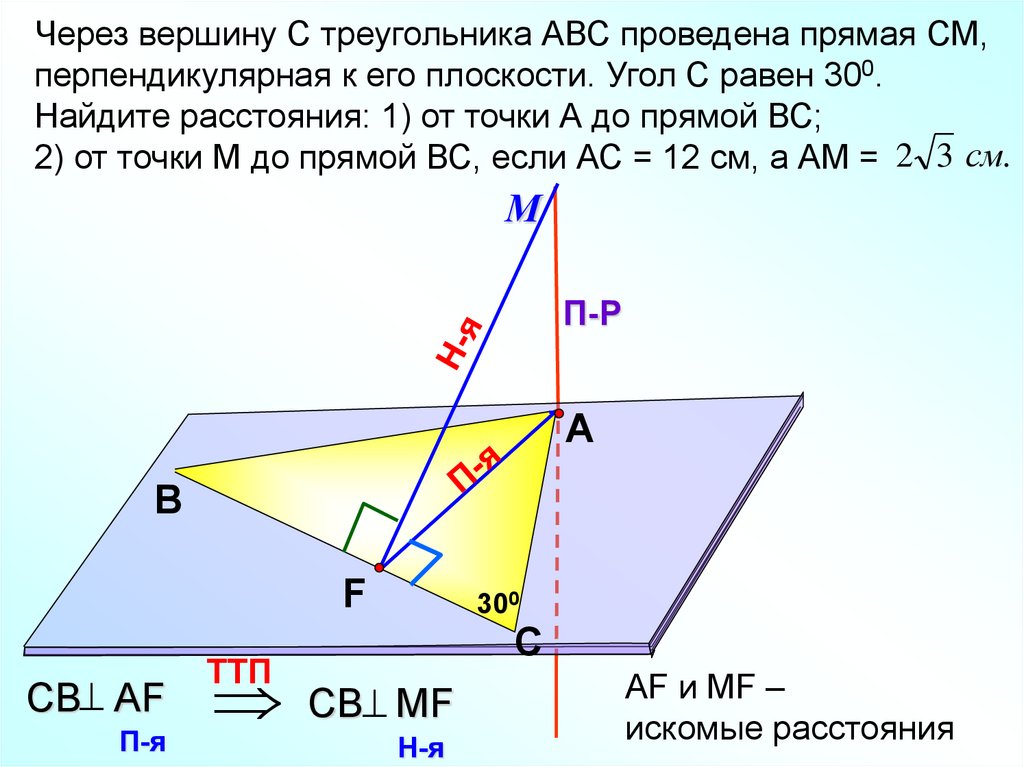
Через вершину С треугольника АВС проведена прямая СМ,
перпендикулярная к его плоскости. Угол С равен 300.
Найдите расстояния: 1) от точки А до прямой ВС;
2) от точки М до прямой ВС, если АС = 12 см, а АМ = 2 3 см.
М
П-Р
А
В
F
СВ АF
П-я
300
СВ MF
TTП
Н-я
С
АF и МF –
искомые расстояния

6.

Планиметрия
Стереометрия
Углом на плоскости мы
называем фигуру,
образованную двумя
лучами, исходящими из
одной точки.
А
В
С
А
В
С
Двугранный угол

7.

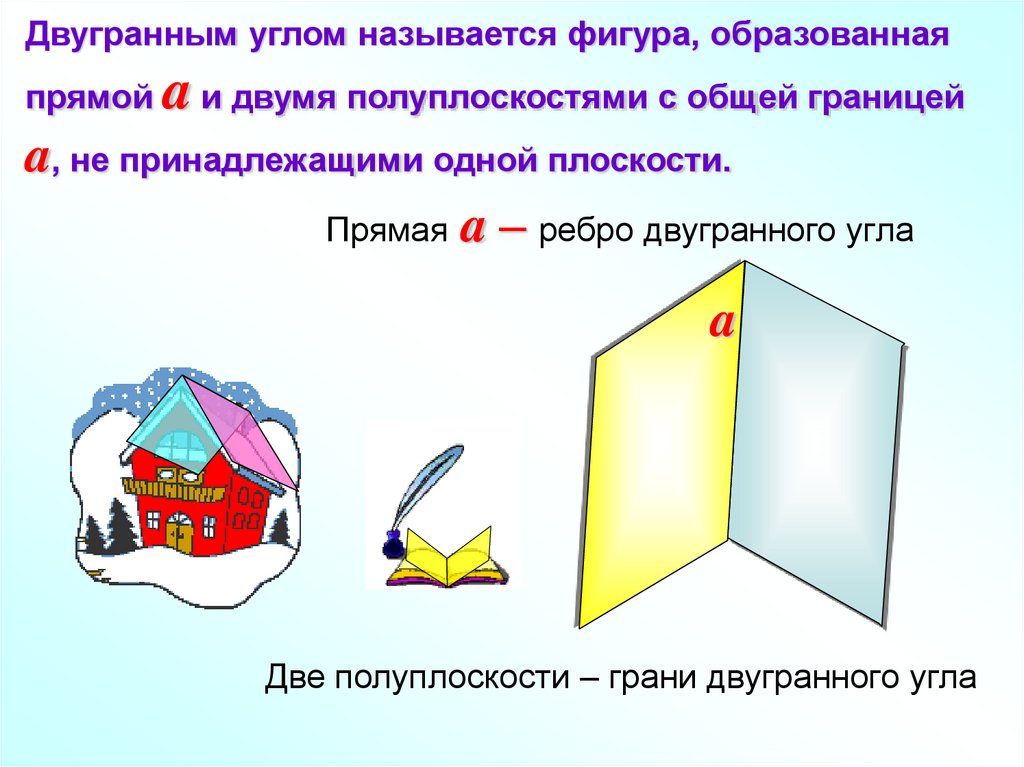
Двугранным углом называется фигура, образованная
прямой
a и двумя полуплоскостями с общей границей
a, не принадлежащими одной плоскости.
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла

8.

Двугранный угол АВNМ, где ВN – ребро, точки А и М
лежат в гранях двугранного угла
D
Угол РDEK
S
O
А
Р
N
F
В
К
X
M
E
Угол SFX – линейный угол двугранного угла

9.

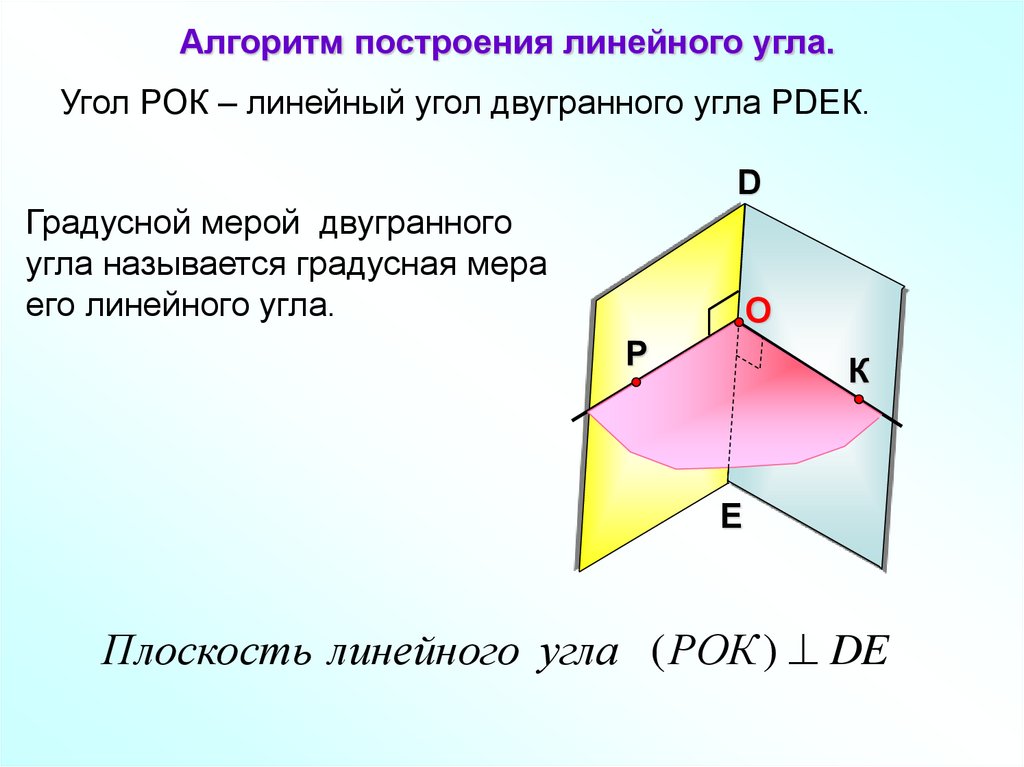
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного
угла называется градусная мера
его линейного угла.
O
Р
К
E
Плоскость линейного угла ( РОК ) DE

10.

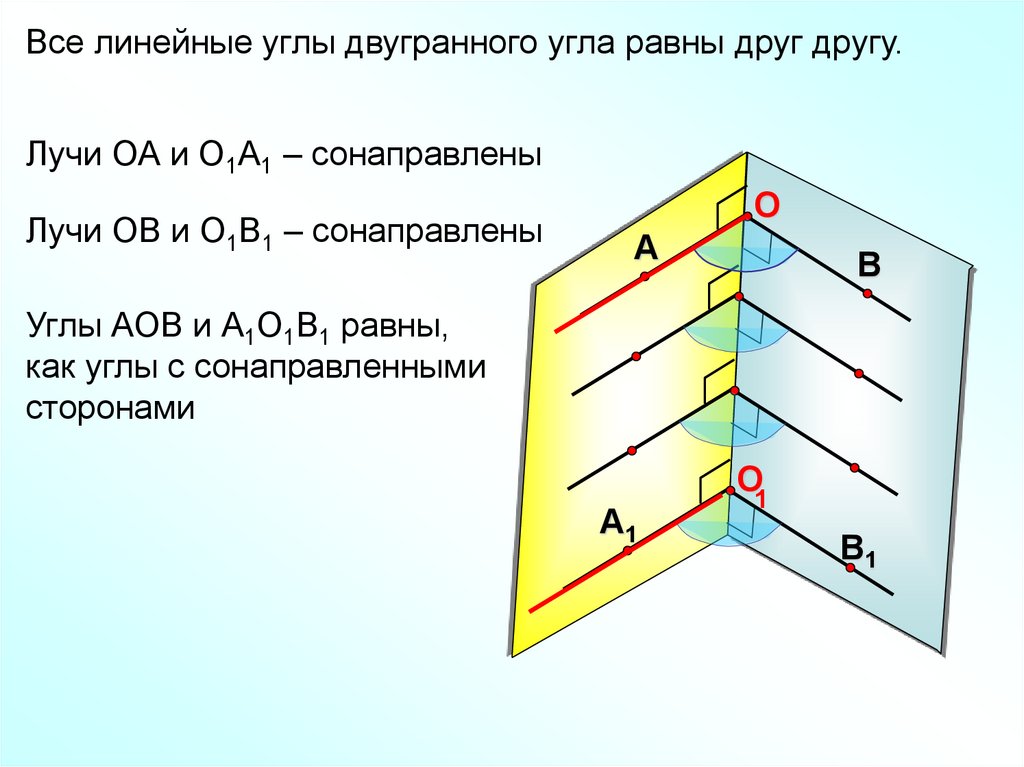
Все линейные углы двугранного угла равны друг другу.
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
O
А
В
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными
сторонами
O
А1
1
В1

11.

Двугранный угол может быть прямым, острым, тупым

12.

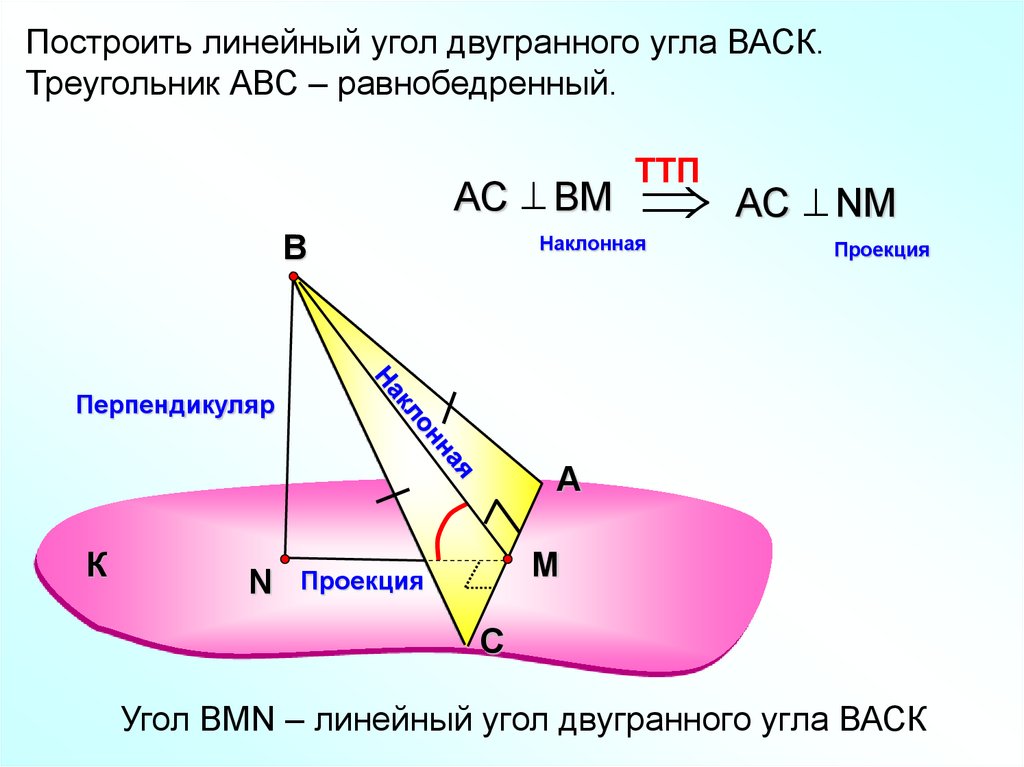
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
АС ВМ АС NМ
TTП
В
Наклонная
Проекция
Перпендикуляр
А
К
N
M
Проекция
С
Угол ВMN – линейный угол двугранного угла ВАСК

13.

Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
АС ВС
АС NС
TTП
Наклонная
Проекция
В
Перпендикуляр
А
К
С
N
Угол ВСN – линейный угол двугранного угла ВАСК

14.

Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
АС ВS
H-я
АС NS
TTП
П-я
В
Перпендикуляр
А
К
С
S
N
Угол ВSN – линейный угол двугранного угла ВАСК

15.

Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
TTП
DС BС
H-я
DС NС
П-я
В
D
Перпендикуляр
К
С
N
Угол ВСN – линейный угол двугранного угла ВDСК

16.

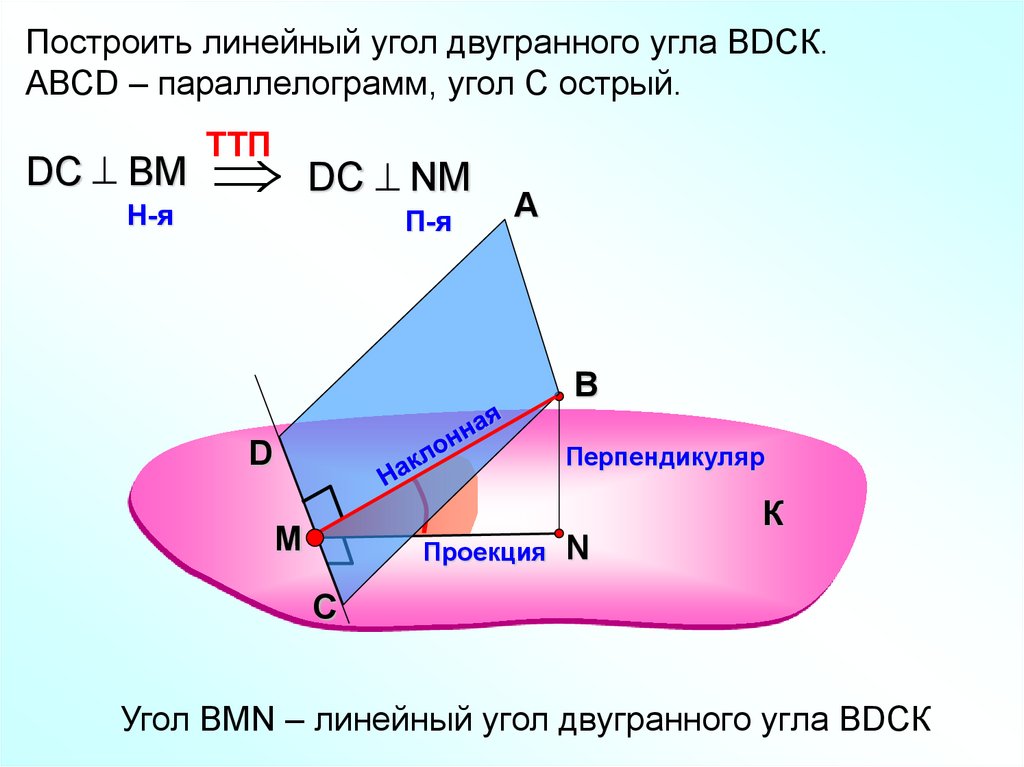
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
DС ВM DС NM
TTП
H-я
П-я
А
В
D
Перпендикуляр
К
M
Проекция
N
С
Угол ВMN – линейный угол двугранного угла ВDСК

17.

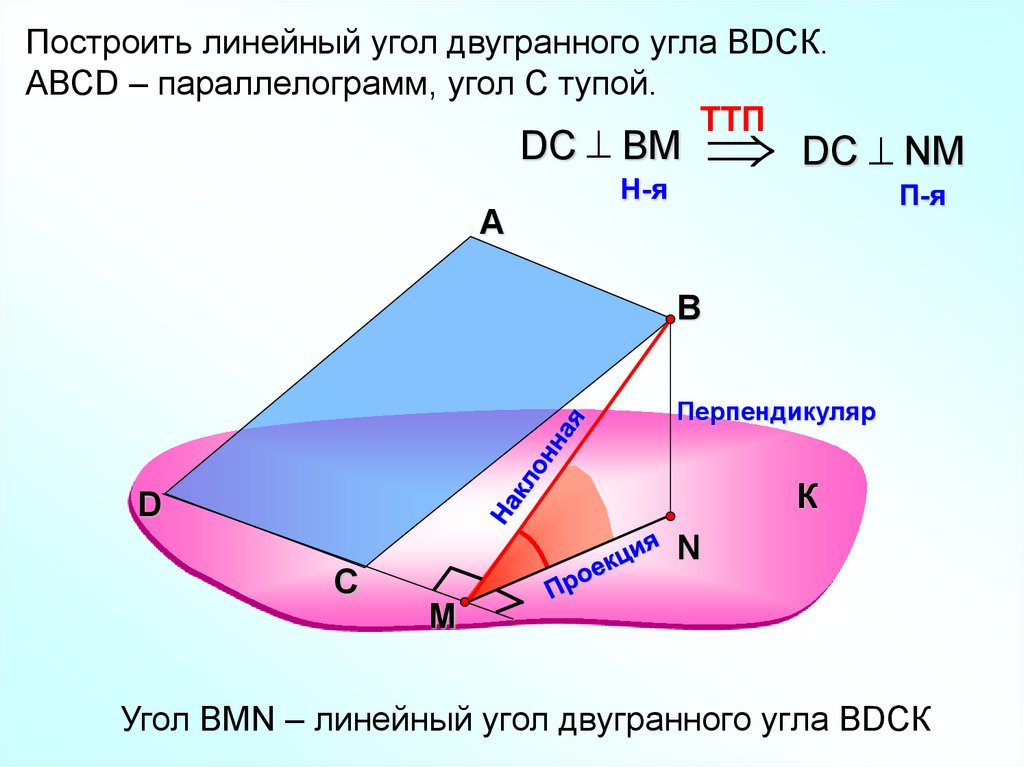
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
TTП
DС ВM DС NM
А
H-я
П-я
В
Перпендикуляр
К
D
N
С
M
Угол ВMN – линейный угол двугранного угла ВDСК

18.

Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
TTП
DС ВM DС NM
H-я
А
П-я
В
Перпендикуляр
К
D
N
M
С
Угол ВMN – линейный угол двугранного угла ВDСК

19.

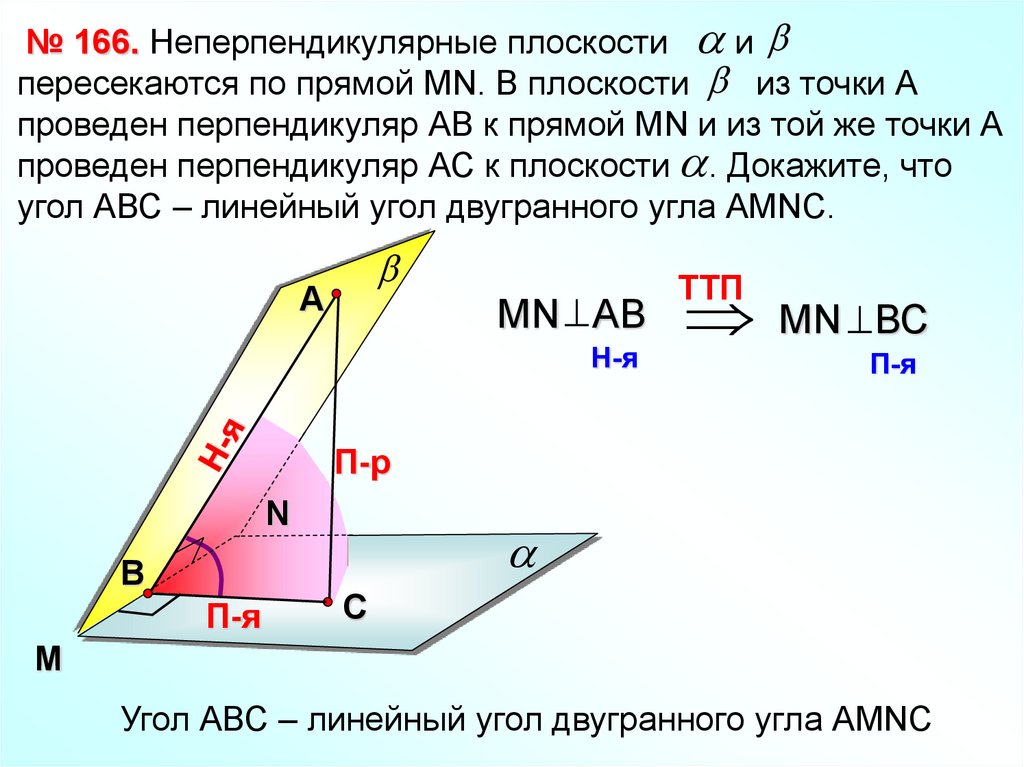
№ 166. Неперпендикулярные плоскости и
пересекаются по прямой МN. В плоскости из точки А
проведен перпендикуляр АВ к прямой МN и из той же точки А
проведен перпендикуляр АС к плоскости . Докажите, что
угол АВС – линейный угол двугранного угла АМNC.
А
МN АB
H-я
MN ВС
TTП
П-я
П-р
N
В
П-я
С
M
Угол АВС – линейный угол двугранного угла АМNC

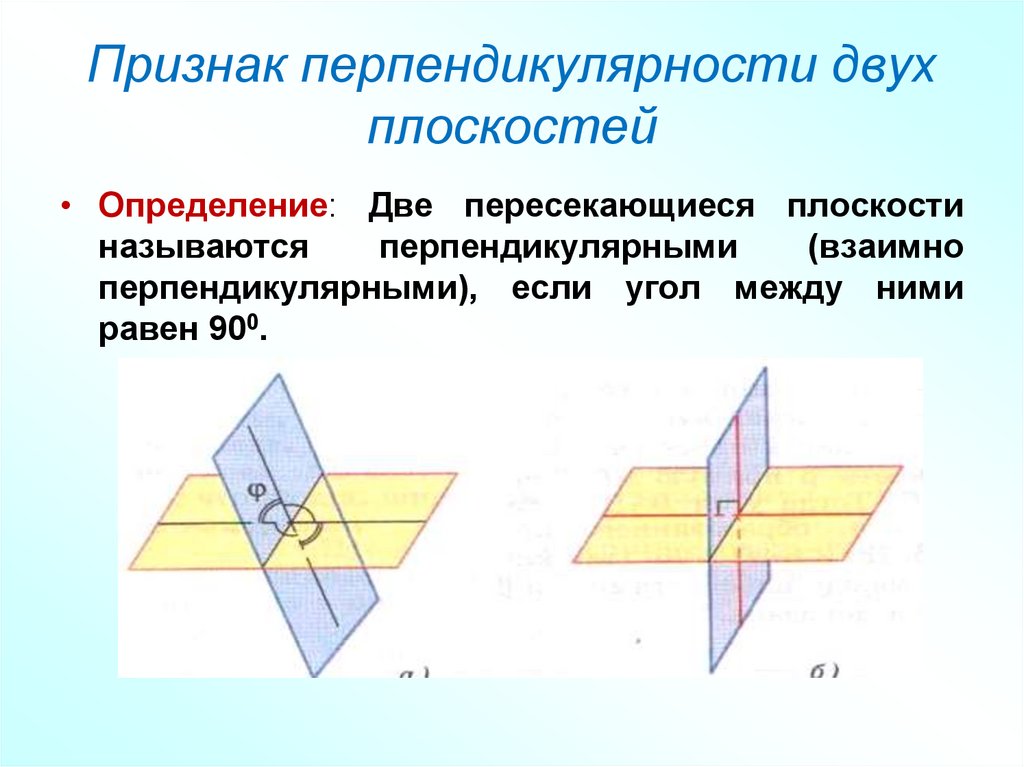
20. Признак перпендикулярности двух плоскостей

• Определение: Две пересекающиеся плоскости
называются
перпендикулярными
(взаимно
перпендикулярными), если угол между ними
равен 900.

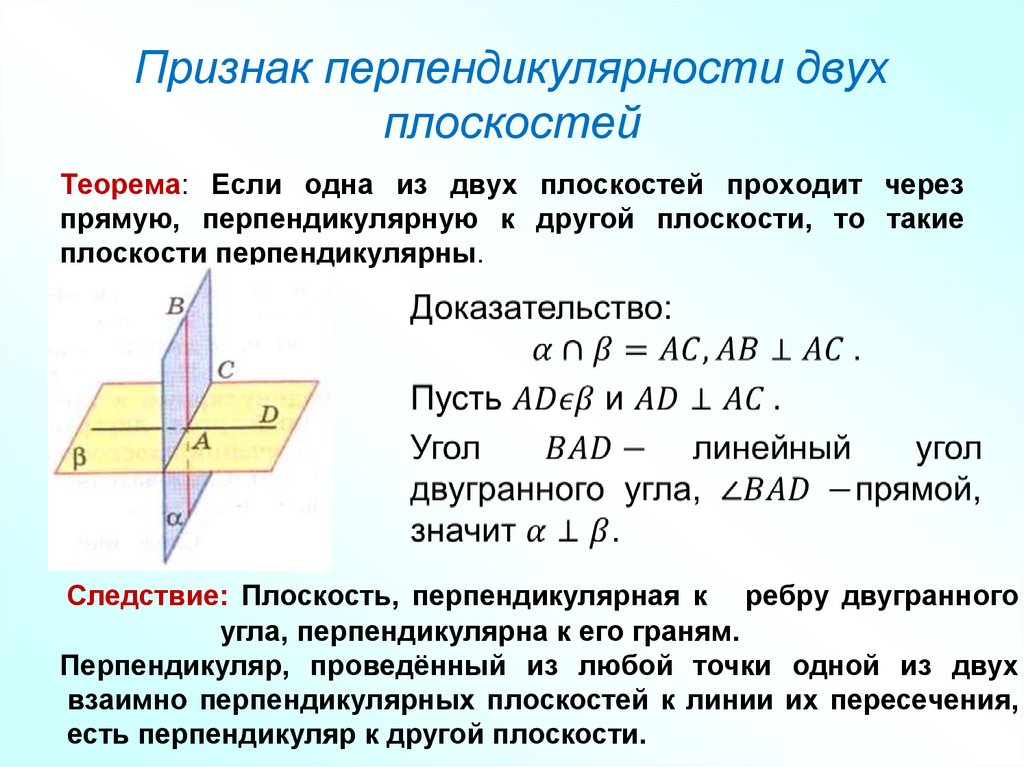
21. Признак перпендикулярности двух плоскостей

Теорема: Если одна из двух плоскостей проходит через
прямую, перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
Следствие: Плоскость, перпендикулярная к ребру двугранного
угла, перпендикулярна к его граням.
Перпендикуляр, проведённый из любой точки одной из двух
взаимно перпендикулярных плоскостей к линии их пересечения,
есть перпендикуляр к другой плоскости.