Третий признак подобия треугольников

1. Третий признак подобия треугольников

2.

Повторение
Определение: треугольники называются подобными,
--------------------------------В1
В
С1
А1
А1=
А1В1
АВ
А,
В1 =
В1С1
ВС
С
А
В,
С1 =
А1С1
АС
С,
k.
A1B1C1
~
ABC,
K – коэффициент подобия
Сходственными сторонами в подобных треугольниках
называются стороны, ---------------------------------------------
Первый признак подобия треугольников: -----------------------------Второй признак подобия треугольников: -------------------------------

3.

Теорема. Если три стороны одного треугольника
пропорциональны трём сторонам другого треугольника,
то такие треугольники подобны.
B
Дано:
P
АВС и
АВ
МР
A
C
1
2
K
M
АВ1
МР
АС
МК
В1С , а по условию АВ
РК
МР
~
АС
ВС
МК
РК
Значит, АВ1 = АВ, В1С = ВС, следовательно, по трём сторонам
Получим:
1=
ВАС,
2=
АС
МК
Доказать:
АВС
Доказательство:
В1
Рассмотрим
АВ1С, у которого
1 = М,
Тогда по двум углам треугольники АВ1С и МРК подобны, значит,
АСВ,
и, учитывая равенства (*), получим: ВАС = М,
АСВ =
Следовательно, АВС и МРК подобны по двум углам.
К.
МРК,
ВС
РК
МРК.
2=
АВ1С =
К (*).
АВС.

4.

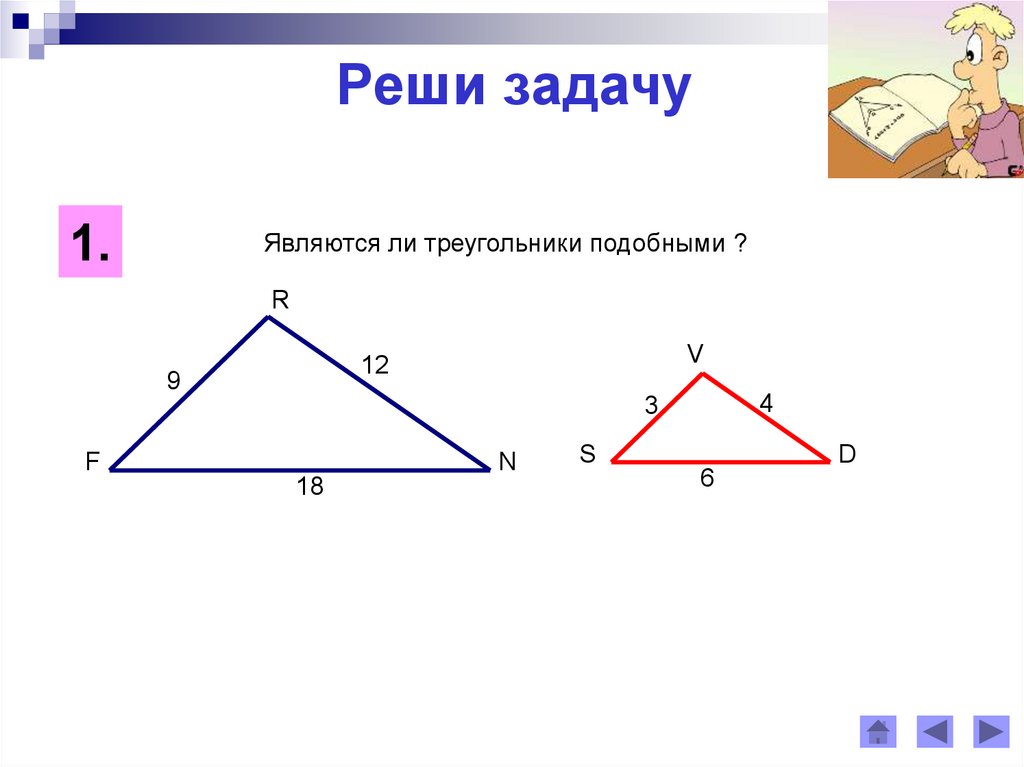
Реши задачу
1.
Являются ли треугольники подобными ?
R
V
12
9
4
3
F
N
18
S
D
6

5.

Реши задачу
2.
В
4
2,5
А
М
5
К
20
С
10
16
Р
Доказать подобие треугольников и выяснить взаимное расположение
прямых ВС и МР.

6.

Реши задачу
3.
Являются ли треугольники подобными ?
N
B
4
8
C
3
F
700
R
A
6
Найти величины остальных углов треугольников.

7.

Реши задачу
4.
Являются ли треугольники подобными ?
8
4
5
10

8.

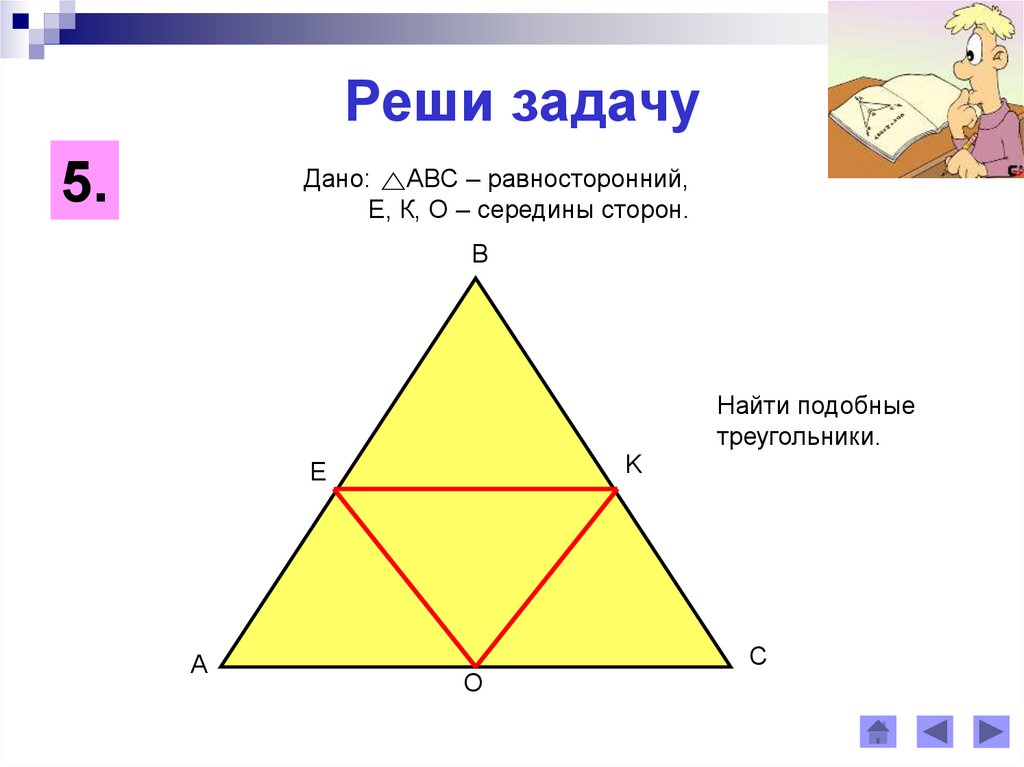
Реши задачу
5.
Дано: АВС – равносторонний,
Е, К, О – середины сторон.
B
Найти подобные
треугольники.
K
E
A
C
O

9.

Решение задачи
В треугольнике АВС АВ = 4, ВС= 6, АС = 7. Точка Е лежит
на стороне АВ. Внутри треугольника взята точка М так, что
МВ = 5,25; МЕ = 4,5; АЕ = 1. Прямая ВМ пересекает АС в точке Р.
Докажите, что треугольник АРВ – равнобедренный.
В
Дано: АВС, АВ = 4, ВС = 6, АС = 7,
АЕ = 1; МВ = 5,25; МЕ = 4,5.
6
5,25
4
С
Доказать:
АВР – равнобедренный.
4,5
Е
М
1
Доказательство:
Р
7
А
ВЕ = АВ – АЕ = 4 – 1 = 3.
Рассмотрим
АВС и
Найдём их отношение:
ВЕМ. 4; 6; 7 и 3; 4,5; 5,25 – длины их сторон.
4
6
7
ВС
- верно, значит, АВ
4,5
5,25
3
МЕ
ВЕ
АС
МВ
Следовательно, треугольники АВС и ВЕМ подобны по трём сторонам, значит,
соответственные углы равны:
Значит,
А=
АВР – равнобедренный.
МВЕ, т. е.
А=
АВР,

10.

Михайлова Л. П.
ГОУ ЦО № 173.