Similar presentations:
Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісімен шешу
1. Параболалық теңдеуге қойылған бастапқы-шеттік есепті Галеркин әдісімен шешу
Орындаған:Джамалова А.Б
1
2.
МақсатПараболалық теңдеуге қойылған
бастапқы-шеттік есепті Галеркин
әдісін пайдаланып сандық әдіс
арқылы жуық шешімін табу
2
3. Есептің қойылымы
D ( x, t ) R : a x b, t 02
Жазық облыста
u K u
2u
L[u( x, t )] K 2 ( x, t )u g ( x, t ),
t x x
x
u ( a, t )
a
u
(
a
,
t
)
a
a 2 (t ),
0
1
x
b u (b, t ) b u (b, t ) b (t ),
0
1
2
x
шеттік шарттарын және
(1)
(2)
(3)
u ( x,0) f ( x),
бастапқы шарттарды қанағаттандыратын U ( x, t ) шешімін табу керек.
2/6/2019
Thema/ Student
3
4.
'Мұндағы K ( x, t ), K x ( x, t ), ( x, t ), g ( x, t ), a 2 (t ), b2 (t ) D облысында үзіліссіз
функциялар.
( K ( x, t ) 0); a0 , a1 , b0 , b1 берілген нақты сандар және a 02 a12 0 ,
b02 b12 0; f ( x) [a, b] -да
туындысымен бірге үзіліссіз және де
келесі шарттарды қанағаттандырады
a0 f (a) a1 f ' (a) a2 (0),
b0 f (b) b1 f ' (b) b2 (0).
2/6/2019
Thema/ Student
4
5.
D облысында екі рет дифференциалданатынu0 ( x, t ), u1 ( x),..., un ( x)
u0 ( x, t ) - (2) шеттік шарттарды қанағаттандыратындай ,
ui ( x)
(i 1) - сынақ функциялары [a, b] да сызықты тәуелсіз және
біртекті шеттік
'
a
u
(
a
)
a
u
0
1 ( a ) 0,
'
b
u
(
b
)
b
u
1 (b) 0.
0
шарттарды қанағаттандырадай аламыз.
n
u n ( x, t ) u 0 ( x, t ) k (t )u k ( x)
(4)
k 1
2/6/2019
Thema/ Student
5
6.
(1) теңдеудегіu n ( x, t )
функциясын u ( x, t ) функциясының орнына қойып,
R1 сәйкессіздікті аламыз
2u0 n
d k
u0
''
R1 ( 1 (t ), 2 (t ),..., n (t ), x, t )
u k ( x)
K ( x, t ) 2 k u k
t
k 1 dt
x k 1
n
n
K u0 n
'
k uk ( x, t ) u0 k uk g ( x, t )
x x k 1
k 1
немесе
d k n '' K '
R1 ( 1 (t ), 2 (t ),..., n (t ), x, t ) u k
Ku k u k u k k
dt k 1
x
k 1
n
u 0 K u 0
u 0
K 2
u 0 g
x x
t
x
2
2/6/2019
Thema/ tudent
(5)
6
7.
un (x,0)ді (3) бастапқы шартқа қойып,
n
R2 ( 1 (0), 2 (0),..., n (0), x) u0 ( x,0) k (0)uk ( x) f ( x)
(6)
k 1
R2 сәйкессіздігін
аламыз.
k (t ) функциясы және k (0) бастапқы мәндерінде
сәйкессіздік қандай да бір мағынада аз болатындай етіп
қосымша шарттар береміз .
2/6/2019
Thema/ Student
7
8.
Жалпы жағдайда Галеркин әдісінде бұл шарттар төмендегі теңдеулержүйесімен анықталынады:
(7)
R1 1 (t ), 2 (t ),..., n (t ), x, t , wk ( x) 0,
k 1, n;
R2 1 (0), 2 (0),..., n (0), x , wk ( x) 0,
k 1, n;
(8)
мұндағы w1 ( x),..., wn ( x) [a, b] -да берілген сызықты тәуелсіз түзілетін
функциялар; ал
b
V ( x), W ( x) V ( x)W ( x)dx.
a
2/6/2019
Thema/ Student
8
9.
(7) шартты ашып жазайықd j n
n
u 0
'
u j ( x)
j Ku j u j K
dt j 1 x
x x
j 1
u 0
u 0 g ( x, t )
, wk ( x) 0
t
немесе
n
j 1
d j
u j , wk ( Ku 'j ) u j , wk j
dt
j 1 x
n
u
u
K 0 u 0 g ( x, t ) 0 , wk ( x) 0,
t
x x
немесе n
d j
a kj
c kj (t ) j bk (t ), k 1, n;
dt
j 1
2/6/2019
Thema/ Student
(9)
9
10.
Мұндағыb
a kj (u j , wk )
u
j
( x) wk ( x)dx,
(10)
a
'
'' K '
ckj Ku j u j , wk Ku j u j u j wk dx,
x
x
a
b
(11)
u0
u0
bk (t ) K
u0 g ( x, t ) , wk ( x)
t
x x
2u0 K u0
u0
K 2
u0 g wk dx,
x x x
t
a
b
2/6/2019
Thema/ Student
k 1, n,
j 1, n.
(12)
10
11.
Егерде өзіміздің қарауымызғаA (a kj ) n , C (ckj ) n , B (bkj ) n,1 , V ( j ) n,1 ,
енгізсек, онда (9) жүйе матрицалық түрде
dV
A
CV B.
dt
(13)
жазамыз.
Енді (13)-дан
dV
A 1 (CV B )
dt
(14)
аламыз.
2/6/2019
Thema/ Student
11
12.
Ал, енді (8) ашып жазсақ, ондаn
u 0 ( x,0) j (0)u j ( x) f ( x), wk ( x)
j
1
u j ( x), wk ( x) j (0) u0 ( x,0) f ( x), wk ( x) 0;
n
j 1
немесе
u ( x), w ( x)
n
j 1
j
k
j
(0) f ( x) u 0 ( x,0), wk ( x) , k 1, n ;
немесе
a
2/6/2019
j (0) d k ,
kj
Thema/ Student
k 1, n ;
(15)
12
13.
a kjМұндағы
a kj
(10) формуласы арқылы анықталады, ал
b
d k f ( x) u 0 ( x,0), wk ( x) f ( x) u 0 ( x,0) wk ( x)dx.
a
Егер D d k n ,1 матрицасын енгізсек, онда (15)-дан
V (0) A 1 D
(16)
аламыз.
2/6/2019
Thema/ Student
13
14.
Осылайша, (4)-нің сынақ шешімін анықтайтынVk (t ),
k 1, n ,
функцияларын табу үшін (14) нормал жүйесінің (16) бастапқы шарттары
бар n белгісіз сызықты жай дифференциалдық теңдеулер жүйесіне
қойылған
Коши есебін аламыз. Көрсетілген Коши есебін шешіп және осыu n ( x, t )
шешімнен анықталынатын k (t ) функцияларын (4)-ге қойып,
сынақ шешімдерінің құрылуын аяқтаймыз.
2/6/2019
Thema/ Student
14
15.
2/6/2019Thema/ Student
15
16.
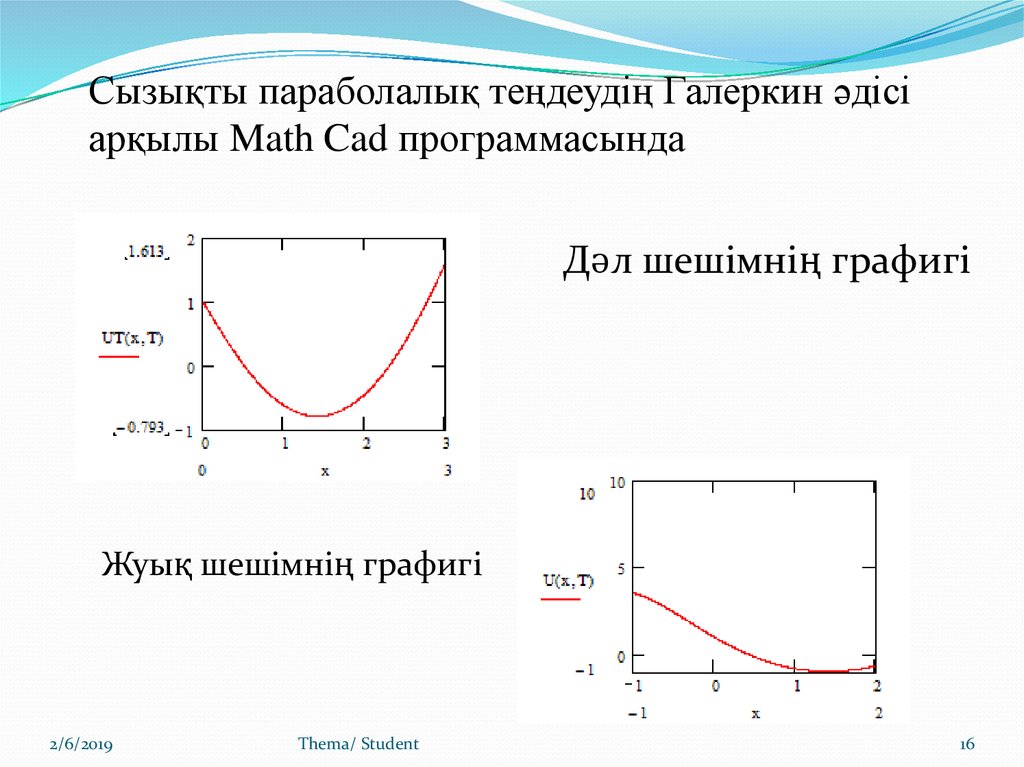
Сызықты параболалық теңдеудің Галеркин әдісіарқылы Math Cad программасында
Дәл шешімнің графигі
Жуық шешімнің графигі
2/6/2019
Thema/ Student
16
17.
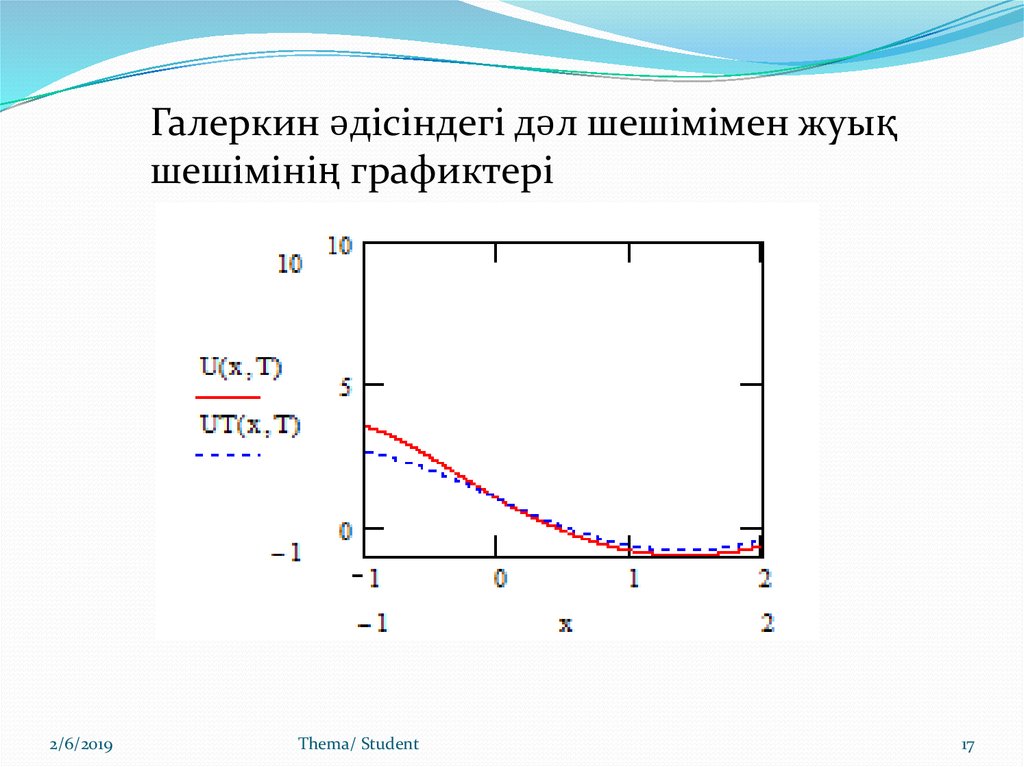
Галеркин әдісіндегі дәл шешімімен жуықшешімінің графиктері
2/6/2019
Thema/ Student
17
18.
Пайдаланылған әдебиеттер1. А. В. Анкилов, П. А. Вельмисов-Алгоритмы методов
взвешенных невязок в системе MATHCAD
2. С.Ю Игнатович-Метод Галеркина решения линейных
граничных задач для дифференциальных уравнений
3. Матвеев Н. М. Дифференциальные уравнения. — Л.:
изд-во Ленингр. ун-та, 1965
18
















 mathematics
mathematics








