Similar presentations:
Ықтималдық және статистика: оқулық
1.
В.Б.МонсикА.А.Скрынников
Ықтималдық және статистика
Ресей Федерациясы жоғарғы оқу орындарының оқу-әдістемелік
бірлестігі мен авиациялық және ғарыш техникасы саласындағы ағарту
бойынша жоғарғы техникалық оқу орындары арасында оқулық ретінде
пайдалануға ұсынылған.
Оқулықта ықтималдықтар теориясының және математикалық
статистиканың теориялық негіздері және қолданбалы әдістері қарастырылған.
Сондай-ақ
«Ықтималдықтар
теориясы
және
математикалық
статистика» пәнін оқытудың жылдық курсы қамтылған.
Теориялық жағдайлар суреттердің молдылығымен қолданбалы
бағыттағы қызықты сандық мысалдармен және есептермен айшықталған,
қосымшаларда оларды шешу үшін қажетті ықтималды-статистикалық
кестелер ұсынылған.
Оқулық жоғарғы оқу орындарының инженерлік мамандық бойынша
білім алып жатқан студенттерге, сонымен қатар оқытушыларға арналған.
УДК 519.2
ББк 22.7
М 77
В.Б.Монсик
М77 Ықтималдық және статистика: оқулық/ В.Б.Монсик, А.А.Скрынников. М.: БИНОМ. Білім зертханасы, 2011. - 381 б.: кес.
ISBN 978-5-9963-06374
2.
УДК 519.2ББК 22.17
Оқу құралы
Монсик Владислав Борисұлы
Скрынников Андрей Александрұлы
Ықтималдық және статистика
Оқу құралы
Аға редактор: И.Я. Ицхоки
Көркемдік редактор: Н.А.Новак
Техникалық редактор: Е.В.Денюкова
Аударған: Сәтбай Жұмағалиұлы Қабақбаев
физика-математика ғылымдарының докторы, профессор
Санкт-Петербург Халықаралық экология және қауіпсіздік
академиясының корреспендент-мүшесі
3.
Алғы сөзОқулық барлық мамандықтардың инженерлерін дайындау, күнделікті
жұмыста ықтималдықты және статистикалық әдістерді қолданатын
оқытушылар, ғылыми қызметкерлер үшін арналған. Ықтималдықтар
теориясының және математикалық статистиканың теориялық негізі және
қолданбалы әдістері қамтылған.
Кітаптың бірінші бөлімінде ықтималдықтар теориясының (ЫТ) негізгі
жағдайлары: ықтималдықтар теориясының негізгі түсініктері, ықтималдылықтар есептерін шешудің комбинаторлық әдістері, ықтималдықтар
теориясының негізгі теоремалары, формулалары, кездейсоқ шамалар,
векторлар және олардың үлестіру заңдары, математикалық статистикада
қолданылатын үлестірудің кейбір заңдары, кездейсоқ аргументтердің
функциялары және ықтималдықтар теориясының шектік теоремалары
қарастырылады.
Екінші бөлімде математикалық статистиканың негіздері: математикалық статистикадағы таңдама әдісі, байқаулардың нәтижелері бойынша
үлестіру заңдарын және кездейсоқ шамалардың моменттік сипаттамаларын
бағалау, болжамдарды статистикалық тексеру беріледі.
Оқулық теориялық жағдайларды кескіндейтін көптеген мәнді мысалдарды қамтиды.
Мысалдар арнайы немесе қандай да бір инженерлік мамандықтарға
бағытталмаған, ал бұл кітаптың әмбебап екендігін көрсетеді. Қолданбалы
есептер практикалық сабақтарда қарастырылады.
Осы оқулықты жазудағы қолданылған оқулықтар және оқу-әдістемелік
басылымдар оқу әдебиеті тізіміне кіргізілген, ал қосымша әдебиет тізімінде
анықтамалық материалдарға сілтемелер берілген.
Кітапта келтірілген мысалдарды және есептерді шешу үшін қажетті
ықтималды-статистикалық кестелер қосымшада ұсынылған.
Кестелерді студенттермен практикалық сабақтар өткізгенде және пәнді
өз бетімен оқығанда, магистранттар емтихан тапсырғанда қолдануға болады.
4.
КІРІСПЕ«Ықтималдықтар теориясы негіздері және математикалық статистика»
пәні қолданбалы математика пәндеріне қатысты, өйткені бұл пән қолданбалы
есептерді шешуге және практикалық қажеттіктен туындаған.
Пәннің екі атауы: бірін-бірі толықтыратын ықтималдықтар теориясы
және математикалық статистика болуы оның екі бағыттан құралатынына
байланысты.
Ықтималдықтар теориясы жалпы кездейсоқ құбылыстардағы
заңдылықтарды оқытады.
Бір және сол тәжірибені (сынауды, экспериментті) бірнеше рет қайта
жүргізгенде барлық жағдайда басқаша өтетін құбылыс – кездейсоқ құбылыс.
Бір және бір ғана тәжірибенің (сынаудың, эксперименттің) бірдей
(өзгермейтін) шарттарда көп рет қайталануының нәтижесі – массалық
кездейсоқ құбылыс.
Кездейсоқ құбылыстардың мысалдарын келтіреміз.
1. Берілген H 0 биіктікте, берілген V 0 жылдамдықпен ұшу аппараты
горизонталь ұшады.
Ұшу аппаратының массасының дұрыс траекториясы теориялықтан –
түзу сызықтан ауытқиды.
Атмосфераның турбуленттілік салдарынан, кездейсоқ желдің екпінінен, ұшу аппаратын басқарудың қателігінен және басқа да әрекеттерден ұшу
аппараты массаның центрінің айналасында толқиды және массаның
центрінің өзінен ауытқиды. Қайтадан ұшқанда ұшу аппаратының дұрыс
қозғалысының траекториялары бірде-бір рет қайталанбайды. Турбуленттік
атмосферада ұшу аппаратының ұшуы – кездейсоқ құбылыстың мысалы.
2. Қандай да бір нысанаға қарудан атыс жүргізіледі. Әрбір атыс үшін
атудың шарты (снарядтың типі, құралды қондырудың бұрышы) бірдей.
Дегенмен, нысанаға қарағандағы снарядтар түсуінің нүктелері шашырау өрісі
деп аталатын өрісті құрайды. Ұшудың теориялық траекториялары беттеседі,
ал кездейсоқ факторлардың болуынан дұрыс траекториялар: снарядтың
салмағының номиналдан (нормадан) ауытқуы, оқ-дәрі зарядының
құрылымының біртексіздігі, снарядты дайындаудың қателігі, ұңғыны
дәлдеудің қателігі, атыс кезіндегі метеорологиялық шарттардың өзгеруі және
т.б. әртүрлі болады. Сондықтан снарядтардың «шашырауын» түсіндіретін
айғақ траекториялар траекториялардың «шоғырын» құрайды. Атыс процесі –
кездейсоқ құбылыс.
3. Бірдей шарттарда бір типті техникалық жүйелердің тоқтаусыз жұмыс
жасауларына сынаулар жүргізіледі. Сынаулардың нәтижесі тұрақты болып
қалмайды, сынаудан сынауға өзгереді. Осы өзгерулер жүйелерді тасымалдау,
жүйешелердің сенімділігі, номиналдан токтың, кедергінің ауытқуы, т.б.
кездейсоқ факторларының әрекеттерінен болады. Техникалық жүйелерді
сынаулардың процесі – кездейсоқ құбылыс.
5.
4. Әуе кемесін берілген маршрутта ұшуға дайындау уақыты, арнайықамтамасыз ету тобының мамандар саны анықталғанда, стандартты отынды
құйғанда қатаң тұрақты шама болып қалмайды, бір әуе кемесінен басқасына
өзгереді. Себептері: әуе кемесінің әртүрлі жағдайы, мамандарды дайындау,
метеожағдай және т.б. кездейсоқ факторлар. Әуе кемесін ұшуға дайындау –
кездейсоқ құбылыс.
5. Симметриялық монета бірнеше рет үстелдің тегіс бетіне
лақтырылады, құлай отырып, өзінің екі жағының бірін ашады: «герб» немесе
"цифр". Сынаудың нәтижесінде «герб» немесе "цифр" түсуі айналудың
бұрыштық жылдамдығы, лақтырылу жылдамдығы, үстелдің бетінің тегіс
еместігі және т.б. кездейсоқ факторлар қатарының әрекеттерінен болады.
Монетаны лақтыру кездейсоқ құбылыс. Кездейсоқ құбылыстардың
негізгі ерекшелігі – олардың нәтижесін алдын ала білу мүмкін емес. Бірақ
бұл кездейсоқ құбылыстар себепсіз дегенді білдірмейді. Ұшу аппаратының
ұшуының бірқалыпты және түзу сызықты, снарядтың қозғалысын,
техникалық жүйенің тоқтаусыз жұмыс жасау уақытын, әуе кемесінің ұшуға
дайындау мезгілін, үстелдің бетіне симметриялық монетаның құлау кезін
анықтайтын негізгі заңдылықтар табылады.
Диалектиканың негізгі заңы – жалпы байланыстылық және құбылыстардың болу заңына сәйкес әрбір құбылыс басқа әртүрлі құбылыстармен
ақырсыз санды байланыста болады.
Барлық осы ақырсыз байланыстар жиынын бақылап отыру мүмкін
емес, сондықтан кездейсоқ құбылыстардың нәтижесін көрсету де мүмкін
емес. Тәжірибеде кез келген заңдылықтар әрқашан қандай да бір
ауытқулармен орындалады.
Ықтималдықтар теориясында оқытылатын пән – «массалық» (жаппай)
кездейсоқ құбылыстар – бірдей жағдайларда көп рет қайтадан болатын
құбылыстар. Осындай кездейсоқ құбылыстар үшін, олардың кейбір орташа
сипаттамаларының орнықтылығы – «статистикалық» заңдылық деп аталатын
сипаттамасы. Кездейсоқ құбылыстардың жүзеге асуының саны көп болуы
қарастырылғанда, осы сипаттама көрнекті көрінеді. Шынында, атыстардың
саны көп болғанда нысанаға қарағандағы снарядтардың шашырау
картинасын байқауға және атудың дәлдігін жорамалдауға болады.
Техникалық жүйелердің тоқтаусыздығын сынаудан өткізгенде тоқтауға
кететін орташа уақытты және ортаның айналасындағы нәтижелердің
шашырауын жорамалдаймыз. 1000 симметриялық монеталарды тегіс бетке
лақтырғанда, орташа 500 монеталар гербпен (цифрмен) жоғары қарап
жатады. Ф. Энгельсше өрнектесек, заңдылық әрқашан өзіне жолды
кездейсоқтар тізбегі арқылы салады.
Сонымен, көптеген практикалық есептерді шешу үшін зерттеудің
ықтималдық немесе статистикалық әдістерін қолданудың негізі – кездейсоқ
құбылыстардың массалық орнықтылығы болатыны практикада көп рет
дәлелденген. Осы әдістер массалық кездейсоқ құбылыстардың орташа,
қосындылық нәтижелерін алдын ала айтуға мүмкіндік береді, әрқайсысының
нәтижесі анықталмай қалады.
6.
Ықтималдықтар теориясы, басқа қолданбалы ғылым сияқты, сандықесептеулер үшін тәжірибелік берілгендерді қажет етеді. Осы берілгендерді
математикалық статистика береді, ықтималдық теориясының бөлімі
секілді құрылған, тіркеу әдістерін жасаумен, тәжірибелердің (байқаулардың,
сынаулардың, эксперименттердің) нәтижелерін өңдеу және талдаумен
шұғылданады.
Ықтималдықтар теориясы сияқты, математикалық статистика,
кездейсоқ құбылыстармен жұмыстас және онымен бірдей анықтамаларды,
түсініктерді, әдістерді қолданады. Дегенмен, математикалық статистика
әдістерімен шешілетін есептер, ерекше сипатқа иелік етеді. Ықтималдықтар
теориясы, олардың моделі толық берілген құбылыстарды зерттейді және
тәжірибеге дейін тәжірибені өткізгеннен кейін болатын статистикалық
заңдылықтарды айқындайды. Математикалық статистикада ықтималдылық моделі белгісіз параметрге дейінгі дәлдікпен анықталған.
Параметрлер жөніндегі мәліметтердің болмауы «байқау» сынауларының
өткізулерімен толықтырылады және олардың негізінде жетіспейтін ақпарат
қалпына келтіріледі.
Математикалық статистикада зерттеулердің екі бағыты бөлінеді.
Біріншісі, тәжірибелердің нәтижелері бойынша үлестірулердің белгісіз
параметрлерін: оқиғалардың ықтималдықтарын, кездейсоқ шамалардың
моменттерін, кездейсоқ шамалардың үлестірулерінің заңдарын бағалаулармен байланысты. Екінші бағыт параметрлерге және кездейсоқ шамалардың
үлестірулеріне қарағанда кейбір априорлы ұйғарымдарды немесе статистикалық болжамдарды тексерумен байланысты.
Ықтималдықтар теориясы зерттеудің қуатты құралы болып табылады,
сондықтан ол ғылымның және техниканың әртүрлі салаларында әртүрлі
қолданыстарда пайдаланылады. Оның қолдану саласы үзіліссіз кеңеюде. XIX
ғасырда ықтималдықтар теориясы атыс теориясында, физикада қолданылды.
XX ғасырда аэродинамикада, гидродинамикада, радиотехникада, басқару
теориясында, ұшу теориясында, байланыс теориясында, құрылыс
механикасында, кеме құрылысында, метеорологияда және басқа да білімнің
салаларында қолданыла бастады. Қазіргі басқару процестері теориясында,
радиотехника теориясында ықтималдықтар теориясы зерттеудің негізгі
құралы болды. Атыс және бомба лақтыру, ұрыс тиімділігі және
операцияларды зерттеу теориялары үшін бұл пән негізгі құрал. Осының
салдарынан ықтималдықтар теориясының қазіргі ғылым және техника
дамуында маңызы өте зор.
XVII ғасырда ықтималдықтар теориясының қажеттілігі құмар ойындардағы кездейсоқ құбылыстардың оқытылуымен түсіндіріледі. Оның дамуы
Б. Паскаль (1623–1662), П. Ферма (1601–1665) және Х. Гюйгенс (1629–1695)
зерттеулерімен байланысты. Якоб Бернулли (1654–1705) массалық кездейсоқ
құбылыстардың негізгі заңдылығын – үлкен сандар заңының математикалық
тұжырымын бірінші рет шығарды. Өлшеулердің қателік бағаларына,
ықтималдық теориясы және оның қосымшаларының келесі дамуында А.
7.
Моавр (1667–1754), П. С. Лаплас (1749–1827), К. Р. Гаусс (1777–1855) жәнеС. Пуассон (1781–1840) зерттеулері өте маңызды орын алды.
XIX ғасырдың соңы мен XX ғасырдың басында Петербург математикалық мектебінің орыс ғалымдары: В. Я. Буняковский (1804–1889),
П. Л. Чебышев (1821–1894), А. А. Марков (1856–1922), А. М. Ляпунов
(1857–1918) ықтималдықтар теориясының дамуында шешуші орын алды.
Біздің заманның ірі математиктерінің бірі, ресейлік ғалым, академик
А. Н. Колмогоровтың ықтималдықтар теориясының математикалық негіздерін жасаудағы алатын орны өте ерекше. Ол аксиомалардың қазіргі жүйесін
жасады және бірінші (1933) болып ықтималдықтар теориясының қатаң
құрылымын берді. С. Н. Бернштейннің, А. Я. Хинчиннің, Е. Е. Слуцкийдің,
Ю. В. Прохоровтың, В. С. Пугачевтің және басқа да ресейлік ғалымдардың
еңбектері қазіргі ықтималдықтар теориясында маңызды орын алады.
8.
1-БӨЛІМЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ
1-ТАРАУ
Ықтималдықтар теориясының негізгі түсініктері
1.1.Тәжірибе және оқиға
Ықтималдықтар теориясында ¿ Ш >¿ шартының және ¿ Ә> ¿ әрекетінің
жиынтығының орындалуы тәжірибе (сынау) деп аталады:
¿ тәжірибе> ¿ ¿
Тәжірибенің нәтижесі оқиға деп аталады, басқаша айтқанда,
тәжірибенің нәтижесінде пайда болуы да немесе пайда болмауы да мүмкін
кез келген айғақ.
Тәжірибенің нәтижесі кездейсоқ болады. Яғни тәжірибенің нәтижесі
кездейсоқ оқиға, ал жалпы мағынада оқиға кездейсоқ делінеді.
Кездейсоқ оқиғалар латын әліпбиінің бас әріптерімен белгіленеді:
A , B , C , D , E , … Басқа әліпбидің әріптері де қолданылуы мүмкін.
1.1.1-мысал. Тегіс үстелдің бетіне симметриялық монетаны бір рет лақтырудың
тәжірибесі жүргізіледі. Мүмкін оқиғалар: Г – гербтің пайда болуы, Ц – цифрдің пайда
болуы. Тәжірибенің нәтижесінде не Г оқиғасы не Ц оқиғасы пайда болуы мүмкін.
1.1.2-мысал. Тегіс үстелдің бетіне бір рет ойын сүйегін лақтыру. Мүмкін оқиғалар
A1 , A 2 ,… , A6 – бір, екі,..., алты ұпайлардың пайда болуы. Көрсетілген оқиғалардың кез –
келгені пайда болуы мүмкін.
1.1.3-мысал. Нысанаға бір рет оқ атады. Мүмкін оқиғалар: A - нысанаға тиеді, B тимейді. Нәтижесінде не A не B пайда болуы мүмкін.
Қарастырылған мысалдарда оқиғалар қарапайым оқиғаларға жіктелмейді. Ондай оқиғаларды элементар оқиғалар немесе тәжірибелердің элементар нәтижелері деп атайды. Элементар оқиғалар жиыны оқиғалардың
толық кеңістігін құрайды. Оқиғалардың толық кеңістігін Ω символымен, ал
элементар оқиғаны ω символымен белгілейік. Сонда бұрын қарастырылған
мысалдар үшін оқиғалардың толық кеңістіктерін былай көрсетуге болады:
1.1.1-мысал. ω 1=Г , ω2= Ц ; Ω={ ω 1 , ω 2 } ;
1.1.2-мысал. ω k = A k , k =1 ,… , 6 ; Ω={ ω 1 , ω 2 , … , ω6 } ;
1.1.3-мысал. ω 1= A , ω2=B ;Ω={ ω1 , ω2 } .
Кездейсоқ оқиғалар элементар оқиғалардың жиынында құрылады.
1.1.2-мысалының шартын қарастырамыз. E оқиғасы сүйекті лақтырғанда үш ұпайдан аз емес оқиғаның пайда болуы:
E={ ω 3 , ω 4 , ω5 , ω6 } деп көрсетіледі.
D – екі оқиғадан көп емес оқиғаның пайда болуы:
D= { ω1 , ω2 } ;
E және D оқиғаларының
толық
1.1.1-суретінде көрсетейік.
оқиғалар
кеңістігінде
кескінделуін
9.
1.1.1-сурет. Кездейсоқ оқиғаларТәжірибеде әрқашан орындалатын оқиғаны ақиқат оқиға деп атайды
және Ω деп белгіленеді. Берілген тәжірибеде ешқашан пайда болмайтын
оқиға мүмкін емес оқиға деп аталады, ∅ символымен белгіленеді. Мысалы,
ойын сүйегін бір рет лақтырғанда (1.1.2-мысалының шарты) алтыдан көп
емес ұпайдың пайда болуы – ақиқат оқиға, ал жеті ұпайдың пайда болуы –
мүмкін емес оқиға. Сонымен, оқиғалар кездейсоқ, ақиқат және мүмкін емес
болулары мүмкін.
1.1.2-сурет. A оқиғасы
1.1.3-сурет. B оқиғасы
Кескіндеу үшін Веннің* диаграммасы жиі қолданылады. Тәжірибенің
нәтижесінде x кездейсоқ оқиғасы тік төртбұрыштың ішіне ақиқат түседі деп
ұйғарады. A оқиғасы – x нүктесінің дөңгелектің ішіне түседі, B оқиғасы - x
нүктесінің квадрат ішіне түседі. Оқиғалардың қасиеттерін және оларға
қолданылатын амалдарды кескіндеу үшін Веннің диаграммасын пайдаланамыз.
Үйлесімсіз оқиғалар – тәжірибенің нәтижесінде бірге пайда бола
алмайтын оқиғалар (1.1.1-, 1.1.2-, 1.1.3-мысалдар). 1.1.1-мысал – монетаны
бір рет лақтырғанда гербтің және цифрдың пайда болуы; ойын сүйегін бір
рет лақтырғанда бір, екі, ..., 6 ұпайлардың бірге пайда болуы: нысанаға бір
рет оқ атқанда оқтың тиюі және тимеуі. Мына түсініктерді шатыстырмау
керек: дұрыс – «бірге» дұрыс емеспен - «біруақытта». Үйлесімді оқиғалар –
тәжірибенің нәтижесінде бірге пайда болатын оқиғалар. Мысалы, екі
монеталарды лақтырғанда герб және цифрдің пайда болулары, нысанаға екі
рет оқ атқанда тиюі не тимеуі. Кескіндері 1.1.4-, 1.1.5-суреттерде
көрсетілген.
* Джон Венн (John Venn, 1834-1923)- ағылшынның логик-математигі, диаграммалардың
графиктік аппаратын құрған. Негізгі еңбектері «Жағдайдың логикасы» (1866),
«Символдық логика» (1881).
10.
1.1.4-сурет. Үйлесімді оқиғалар1.1.5-сурет. Үйлесімсіз оқиғалар
1.1.6-сурет. Оқиғалардың толық тобы 1.1.7-сурет. Оқиғалардың толық емес тобы
Егер тәжірибенің нәтижесінде саналған оқиғалардың (1.1.1-, 1.1.2-,
1.1.3-мысалдар) ең болмағанда біреуі міндетті түрде пайда болса, онда
оқиғалар толық топты (тәжірибе нәтижелерінің толық кеңістігі)
құрайды. Қарсы жағдайда оқиғалар толық топты құрамайды. Мысалы, бір рет
ойын сүйегін лақтырғанда бір, екі, төрт, бес ұпайлардың пайда болуы –
толық топты құрамайтын оқиғалар (алты ұпай оқиғасы аталмады).
Кескіндеулері 1.1.6-, 1.1.7-суреттерде берілген.
A оқиғасын толық топқа дейін толықтыратын және A оқиғасымен
үйлесімсіз болатын A оқиғасы A оқиғасына қарама-қарсы оқиға (1.1.8-сурет)
A оқиғасынын Ω – ға толықтыруы деп аталады (1.1.1-,
немесе
1.1.3-мысалдар). Мысалы, монетаны лақтырғанда герб және цифр қарамақарсы оқиғалар, нысанағы бір рет оқ атқанда тию және тимеу – карама-қарсы
оқиғалар.
Кейбір сынауларда (тәжірибелерде) симметриялық нәтижелер, (1.1.1-,
1.1.2-мысалдары) бірдей мүмкіндікті (тең мүмкіндікті) алынады. Ондай
оқиғалар тең мүмкіндікті деп аталады.
Күрделі оқиғаларды элементар оқиғаларға жіктеу және керісінше
орындау арқылы оқиғаларға қолданылатын амалдарды қарастырамыз.
11.
1.1.8-сурет. Қарама-қарсы оқиғалар.Оқиғаларды көбейту амалы
Оқиғаларды көбейту амалы A және B оқиғаларының бірге пайда болуы
A және B оқиғаларының көбейтіндісі C деп аталады:
AB=C (1.1.1)
деп жазылады. Кескінделуі 1.1.9-суретте берілген.
Кейде оқиғалардың көбейтіндісін «оқиғалардың қиылысуы» деп
атайды:
A ∩ B=C
түрінде жазылады.
Оқиғаларды көбейту амалы «Ж» логикалық амалына эквивалентті. Осы
мағынада (1.1.1) формуласы былай өрнектелуі мүмкін:
A ж B=C .(1.1 .2)
Басқаша айтқанда, A және Bоқиғалары бірге орындалғанда ғанаC оқиғасы
орындалады. Оқиғалардың көбейтіндісінің мысалдарын қарастырамыз.
1.1.4-мысал. Екі ойын сүйегі лақтырылады. Мына оқиғаларды қарастырамыз: A –
бірінші сүйекте алты ұпайдың пайда болуы, B – екінші сүйекте алты ұпайдың пайда
болуы, C – екі алтының пайда болуы.
C оқиғасының пайда болуы A және Bоқиғаларының пайда болуларынан орындалатындығы айқын, сонымен
C= AB .
1.1.5-мысал. Нысанаға үш рет оқ атылады. Бірінші, екінші, үшінші ату
нәтижелеріндегі A1 , A 2 , A3 оқиғалары қарастырылады. D – үш рет атқандағы оқтардың
тию оқиғасы. Сонда қарапайым
D= A 1 A2 A 3 .
Берілген мысалда үш оқиғалардың көбейтіндісі – D оқиғасы қарастырылады
(1.1.10-сурет).
1.1.9-сурет. Екі оқиғалардың көбейтіндісі
1.1.10-сурет. Үш оқиғалардың көбейтіндісі
12.
Жалпы жағдайда, A1 , A 2 ,… , An бірнеше оқиғаларының көбейтіндісіn
A=∏ A i(1.1.3)
i=1
түрінде белгіленеді және тәжірибеде A1 , A 2 ,… , An оқиғаларының бірге пайда
болуын көрсетеді.
Оқиғаларды қосу амалы
Берілген тәжірибеде A оқиғасы немесе B оқиғасы пайда болуынан
тұратын C оқиғасын, үйлесімсіз A және B екі оқиғаларының қосындысы деп
атаймыз (1.1.11-сурет). A және B оқиғаларының қосындысы:
A+ B=C(1.1 .4)
түрінде жазылады.
Қосу амалы логикалық «НЕМЕСЕ» амалына эквивалентті. Осы
мағынада (1.1.4) формула:
A немесе B=C (1.1.5)
деп жазылады.
Екі үйлесімдіC және D оқиғаларының бірігуі деп, кейбір K оқиғасын
айтамыз, егер K оқиғасы саналған оқиғалар – C оқиғасы немесе D оқиғасы
немесе C және D оқиғаларының берілген тәжірибеде «ең болмағанда
біреуінен» тұрса (1.1.12-сурет). Екі оқиғалардың бірігуін:
C ∪ D=K (1.1 .6)
деп жазамыз.
(1.1.6) формуласы мына логикалық жазылуға эквивалентті:
K=C немесе D немесеCD (1.1 .7)
Оқиғаларды қосуға мысалдар қарастырамыз.
1.1.6-мысал. Үстелдің бетіне ойын сүйегін бір рет лақтырылады. Тәжірибенің
нәтижелері Ai - i ұпайлардың, i=1 , … , 6пайда болу оқиғалары. A5 және A6 оқиғалары
үйлесімсіз болғандықтан, Bоқиғасы – бестен кем емес ұпайлардың пайда болу оқиғалары
мына қосынды түрінде жазылады:
B= A 5+ A 6 .
.
1.1.11-сурет. Екі оқиғалардың қосындысы 1.1.12-сурет. Екі оқиғалардың бірігуі
E оқиғасы – ең болмағанда бір ұпайдың пайда болуы – алты
оқиғалардың қосындысы түрінде өрнектеледі және ақиқат оқиға болады:
E=A 1 + A 2 +…+ A 6=Ω .
Бірнеше үйлесімсіз A1 , A 2 ,… , An оқиғаларының қосындысы:
13.
nA=∑ A i (1.1 .8)
i=1
түрінде жазылуы мүмкін.
1.1.7-мысал. Екі монеталар лақтырылады. Мына оқиғалар қарастырылады: C – ең
болмағанда бір гербтің пайда болуы, D – ең болмағанда бір цифрдің пайда болуы, K – осы
оқиғалардың бірігуі:
K=C ∪ D , K=C немесе D немесе CD .
Нәтижені сызбада түсіндіреміз. Тәжірибенің нәтижелерінің кеңістігін қарастырамыз (1.1.13-сурет).
1.1.13-сурет. Тәжірибелер нәтижелерінің кеңістігі – екі монеталарды лақтыру.
C және D оқиғалары үйлесімді екендігін көреміз, сондықтан K оқиғасы C
оқиғасының пайда болуынан немесе D оқиғасының пайда болуынан немесе C және D
оқиғаларының бірге пайда болуынан орындалады. Басқаша айтқанда, K оқиғасына
берілген тәжірибенің барлық оқиғалары кіретіндіктен, ол ақиқат оқиға.
Бірнеше B1 , B2 , … , Bn үйлесімді оқиғаларының бірігуі:
n
B=∑ Bi (1.1 .9)
i=1
түрінде өрнектелуі мүмкін.
Оқиғаларды азайту амалы
A және B оқиғаларының айырмасы деп, кейбір E оқиғасын айтады,
егер осы оқиға B оқиғасында жататын нәтижелерді A оқиғасындағы
нәтижелерден шығарып тастағаннан кейінгі оқиғалардан құралса:
E=A−B .(1.1 .10)
Оқиғалардың айырмасы 1.1.14-суреттегі диаграммада көрсетілген.
1.1.14-сурет. Екі оқиғалардың айырмасы
1.1.8-мысал. Айталық A оқиғасы A1 , A 2 , A3 , A 4 нәтижелерін кірістірсін
(1.1.6-мысалының шарты): A={ A1 , A 2 , A3 , A 4 }, ал B оқиғасы A3 , A 4 , A 5 , A 6 нәтижелерін
кіргізеді: B={ A 3 , A 4 , A 5 , A6 }, басқаша айтқанда, A – төрттен үлкен емес ұпайлар саны, B ең болмағанда үш ұпайдың болу саны. Сонда айырма:
E=A−B={ A 1 , A 2 } .
14.
Толықтыру амалыA оқиғасының Ω оқиғасына дейін толықтыруы A болады, A мен
үйлесімсіз A оқиғасы толық топты құраса. A -ның Ω-ға дейінгі толықтыруын
мына айырма түрінде өрнектейміз:
A=Ω− A .(1.1 .11)
1.1.15-сурет. А оқиғасының толық кеңістікке дейін толықтыруы
A және A оқиғалары қарама-қарсы оқиғалар деп аталады. Қарама-
қарсы оқиғалар үшін келесі қатынас дұрыс болады:
A+ A=Ω ,(1.1 .12)
A A=∅.(1.1 .13)
Қарама- қарсы оқиғалардың мысалдары:
1. Үш монетаны лақтырғанда ең болмағанда бір гербтің пайда болуы – A оқиғасы.
Үш цифрдің пайда болуы (бірде-бір герб болмайды) - A оқиғасы.
2. Бес рет атқанда ең болмағанда, үш рет тиюі – B оқиғасы. Үштен аз тиюі - B .
3. Крамниктің Каспаровты ұтуы – D оқиғасы. Крамниктің Каспаровты ұтпауы
(Крамниктің тең түсуі немесе ұтылуы) - D оқиғасы.
Ықтималдылық есептерін шешуде қарама-қарсы оқиғалардың жиі
қолданылатындығы төменде қарастырылады.
1.2. Оқиғаның жиілігі және ықтималдығы
Бірдей n тәжірибелердің тізбегін қарастырамыз. A оқиғасының пайда
болуы немесе пайда болмауы әрбір тәжірибенің нәтижесі деп ұйғарамыз. A
оқиғасының осы тәжірибелердің тізбегіндегі қарапайым сипаттамасы оның
пайда болуының жиілігі – A оқиғасы пайда болғандағы тәжірибелер санының
тәжірибелердің барлық сандарына қатынасы болады. A оқиғасының жиілігін
P¿ ( A) , ал n тәжірибелердегі оқиғалардың пайда болу санын m A арқылы
белгілеп, мынаны аламыз:
¿
P ( A)=
mA
.(1.2 .1)
n
Тәжірибенің нәтижесінде ешқашан пайда болмайтын ∅ мүмкін емес
оқиғаның жиілігі:
P¿ ( ∅ ) =
m∅ 0
= =0(1.2.2)
n n
және әрқашан пайда болатын ақиқат оқиғаның Ω жиілігі
¿
P (Ω)=
mΩ n
= =1(1.2 .3)
n n
жиіліктің шектік мәндері болады.
15.
Тәжірибенің нәтижесінде пайда болуы да, пайда болмауы да мүмкінкездейсоқ A оқиғасының жиілігі, нөл мен бірдің аралығында жататындығы
оңай-ақ түсінікті. Сондықтан кез келген оқиғаның жиілігі дұрыс бөлшек,
немесе нөл, немесе бірге тең:
¿
0 ≤ P ( A ) ≤1.(1.2 .4)
Кейде жиілік пайызбен өрнектеледі, сонда (1.2.4):
0 % ≤ P¿ ( A ) ≤ 100 %(1.2 .5)
түрінде жазылады.
Бірдей шарттарда n тәжірибелерден серияларды көп рет қайта өткізгенде әрбір серияда A оқиғасының пайда болу саны m A өзгереді, демек,
оқиғаның жиілігі (1.2.1)-де өзгереді (кездейсоқ болады).
Мысалы, монетаны лақтырудың бірнеше сериялары жүргізілсін, әрбір
серияда монеталар 10 рет лақтырылсын және гербтің пайда болуының (Г
оқиғасы) жиілігі анықталсын
mГ
, (1.2.6)
n
мұнда mГ – әрбір серияда гербтің пайда болуының саны. Әрбір серияда mГ
¿
P ( Г )=
шамасы нөлден онға дейінгі кез келген мәндерді қабылдайтындықтан, (1.2.6)
жиіліктерінің мәндері бір-бірімен тең болмауы мүмкін, демек, кездейсоқ.
Оқиғаның жиілігі, тәжірибелердің санын шексіз үлкен өсіргенде
оқиғалардың жиіліктері де кейбір тұрақты шамаға шексіз жуықтайтындығын
көрсететін тамаша орнықтылық қасиетімен сипатталады. Жиіліктің орнықтылығын сипаттайтын екі мысалды қарастырамыз.
1-кестеде монетаны лақтырғандағы жиіліктерді бақылаған белгілі
ғалымдар – статистиктер Ж. Л. Бюффонның, Ч. Пирсонның тәжірибелерінің
нәтижелері келтірілген.
1-кесте
Тәжірибе жасаушы
Монетаны лақтыру
саны
Гербтің пайда
болуы
Жиілік
Бюффон
Пирсон
Пирсон
4040
12000
24000
2048
6019
12012
0,5080
0,5016
0,5005
Кестеде келтірілген нәтижелер гербтің пайда болуының жиілігі 0,5
санына жуықтайтынын көрсетеді, бұл сан Г оқиғасының статистикалық
ықтималдығы деп аталады және P(Г ) деп белгіленеді. Сонымен P ( Г )=0,50.
2-кестеде 1935 жыл үшін Швед статистикасы келтірген әрбір айда
дүниеге келген нәрестелердің үлестері жөнінде мәліметтер келтірілген
(Г.Крамер. «Статистиканың математикалық әдістері») .
¿
Кестеден шығады, қыз балалардың тууының жиілігі P ( Қ) 0,483
санының айналасында толқиды, сондықтан статистикалық ықтималдық
P¿ ( Қ ) =¿ 0,483.
Сонымен, тәжірибелердің саны шексіз өскенде оқиғалардың жиілігі
шексіз жақындайтын санды – статистикалық ықтималдықты енгіздік.
16.
Жиіліктің және ықтималдықтың жинақталу сипатын бірінші рет Я.Бернулли*зерттеді және осыған сәйкес теореманы тұжырымдады.
Егер ε > 0мейлінше аз саны үшін | Х n−a|<ε теңсіздігінің ықтималдығы n
саны шексіз өскенде бірге шексіз жуықтаса, Х n шамасы ықтималдық
бойынша a шамасына жинақты деп айтады.
1
2
3
4
5
6
7
8
9
10
11
12
Жыл
Жаңа
туылған
нәрестелер
саны
7280
6957
7883
7884
7892
7609
7585
7393
7203
6903
6552
7132
88273
Ер
балалардың
саны
3743
3550
4017
4173
4117
3944
3964
3797
3712
3512
3392
3761
45682
Қыз
балалардың саны
3537
3407
3866
3711
3775
3665
3621
3596
3491
3391
3160
3371
42591
Қыз
балалардың
туылуының жиілігі
2-кесте
Ай
0,486
0,489
0,490
0,471
0,478
0,482
0,462
0,484
0,485
0,491
0,482
0,473
0,483
Бұл жиілікке және ықтималдыққа сәйкес мына түрде жазылады:
¿
P (|P ( A )−P ( A )|<ε ) >1−δ , ε >0 , δ> 0 .(1.2.7)
(1.2.7) өрнегі Я. Бернулли теоремасының мазмұнын құрайды: A
оқиғасының жиілігі тәжірибелердің сандары шексіз өскенде ықтималдық
бойынша A оқиғасының ықтималдығына жинақталады.
Оқиғаның P ( A )ықтималдығы берілген тәжірибедегі оқиғаның обьективті мүмкіндігі дәрежесінің сандық өлшемі болады. Оқиғаның ықтималдығының мүмкін мәндерінің жоғары және төменгі шекаралары сәйкесінше
мүмкін емес және ақиқат оқиғалардың ықтималдықтарына тең:
P ( ∅ )=0 , P ( Ω )=1. ( 1.2.8 )
Тәжірибелердің барлық қалған кездейсоқ оқиғалары нөл және бір
арасында жататын ықтималдықтармен бағаланады. Жалпы жағдайда
оқиғаның ықтималдығы нөлден бірге дейін (немесе нөлден 100 пайызға
дейін) жатады:
0 ≤ P ( A ) ≤ 1 немесе0 % ≤ P ( A ) ≤1 00 % (1.2.9)
* Якоб Бернулли (1654–1705) – Швейцария математигі, Базель университетінің
профессоры (1687 жылдан). Ықтималдықтар теориясындағы іргелі жетістіктері – тәуелсіз
қайталанған сынаулардың (Бернулли сынаулары) ықтималдылық моделін жасады. Бірінші
рет үлкен сандар заңын дәлелдеді. Ықтималдықтар теориясы бойынша негізгі еңбегі –
«Ұйғарымдар өнері» (1713 жылы жарыққа шықты).
17.
Ықтималдықтар әдістерін практикада қолданғанда практикалықақиқат және практикалық мүмкін емес оқиғалар маңызды орын алады.
Тәжірибелердің нәтижесінде барлық кезде орындалатын оқиғаны практикалық ақиқат деп атайды. Басқаша айтқанда, мұндай оқиғалардың
ықтималдығы бірге жақын, бірақ бірге тең емес. Мысалы, төтенше жағдайда
өз ұшағын тастап кеткенде ұшқыштың парашютының ашылуы немесе белгілі
фирмада құрастырылған қазіргі заманғы телевизордың жұмысының
сенімділігі – практикалық ақиқат оқиғалар.
Тәжірибелердің нәтижесінде әрқашан дерлік орындалмайтын оқиға
практикалық мүмкін емес оқиға деп аталады. Басқаша айтқанда, ондай
оқиғаның ықтималдығы нөлге жақын,бірақ нөлге тең емес.
Мысалы, төтенше жағдайда өз ұшағын тстап кеткенде ұшқыштың
парашютінің ашылмауы немесе белгілі фирмада құрастырылған қазіргі
заманғы телевизордың жұмыс жасамауы – практикалық мүмкін емес оқиға.
Біз анықталған практикалық мағынаны оқиғаның ықтималдығы түсінігімен
байланыстырамыз:
Жинақталған тәжірибелердің негізінде біз мынаны тұжырымдаймыз –
жиірек орындалатын оқиғалардың ықтималдығы үлкен, ал сирек
орындалатын оқиғалардың ықтималдығы аз. Сонымен, оқиғаның ықтималдығының түсінігі тәжірибелердің нәтижелерімен байланысты, демек, оқиғаның жиілігі түсінігімен де байланысты. Оқиғаның ықтималдығының статистикалық түрде анықталуымен бірге оқиғаның пайда болуының жиілігі
арқылы жағдайлар деп аталатын оқиғаның ықтималдығының классикалық
түрі табылады.
Үйлесімсіз, тең мүмкіндікті (тең ықтималдықты), толық топты
жасайтын оқиғаларды жағдайлар (шанстар) деп атайды. Жағдайлар тобын
жасайтын оқиғалардың мысалдары:
- монетаны бір рет лақтырғанда гербтің және цифрдің пайда болуы;
- ойын сүйегін бір рет лақтырғанда бір, екі, ..., алты ұпайлардың пайда
болуы;
- урнадағы әртүрлі түсті шарлардан қалауынша бірдей шарларды алғанда әртүрлі шарлардың пайда болуы;
Айталық A1 , A 2 ,… , An – үйлесімсіз, тең мүмкіндікті және толық топты
жасайтын оқиғалар , ал A1 , A 2 ,… , An өзімен B оқиғасының пайда болуын
Ai ϲ B , i=1 , … ,m , m≤ n қамтиды. Сонда B оқиғасының ықтималдығы классикалық
формуламен анықталады:
P ( B )=
MB
,(1.2 .10)
N
мұнда N – жағдайлардың жалпы саны, M B –
жағдайлардың саны (өзімен B оқиғасын қамтитын).
Bоқиғасына
қолайлы
1.2.1-мысал. Тәжірибе ойын сүйегін бір рет лақтырумен қорытындыланады.
Оқиғалар қарастырылады:
A – жұп ұпайлардың пайда болуы,
B – үштен кем емес ұпайлардың пайда болуы,
C – ең болмағанда бір ұпайдың пайда болуы.
Осы оқиғалардың ықтималдықтарын анықтаймыз.
18.
Шешуі. Тәжірибелердің нәтижелері – A1 , A 2 , A3 , A 4 , A5 , A 6 – бір, екі, ..., алтыұпайлардың пайда болулары – жағдайлардың тобын жасағандықтан, онда ізделінді
ықтималдықтарды (1.2.10) формуламен есептейміз. A оқиғасына қолайлы нәтижелер
(оқиғалар) A2 , A 4 , A 6 ( M A=3 ) , B оқиғасына қолайлы нәтижелер A3 , A 4 , A 5 , A 6 ( M B=4 ) , C
оқиғасына қолайлы нәтижелер A1 , A 2 ,… , A6 ( M С =6 ). Осы оқиғалардың ықтималдықтары
мынаған тең:
3
4
6
P ( A )= , P ( B )= , P ( C ) = =1=P ( Ω ) .
6
6
6
1.2.2-мысал. Сипап қарауға бірдей, урнадағы 6 ақ және 4 қара шарлардан бір
шарды алады. Алынған шардың ақ (қара) болуының ықтималдығы қандай?
1.2.1-сурет.Урналар сызбасының моделі
Шешуі. Тәжірибенің мүмкін нәтижелерін 10 - Ak оқиғалары , k =1 , … ,10−k
нөмерлі шардың пайда болуы (барлық шарлар әртүрлі және нөмірленген деп ұйғарылады).
Ak оқиғалары үйлесімсіз (10 шардан тек қана біреуі алынады), тең мүмкіндікті (барлық
шар сипап қарауға бірдей) және толық топты жасайды, демек, жағдайлар тобын
құрайтындығы шығады. A – ақ шардың пайда болуы, Қ – қара шардың пайда болуы деп
белгілейміз. A оқиғасына 6 нәтижелер, Қ оқиғасына 4 нәтижелер қолайлы. (1.2.10)
формуласымен ізделінді ықтималдықтарды есептейміз:
MA 6 3
MҚ 4 2
P ( A )=
= = , P ( Қ )=
= = .
N 10 5
N 10 5
1.2.3-мысал. Ойын картасының 36 картадан тұратын колодасынан 3 картаны
қалауынша алады. Алынған картанаң бір тұз (колодадағы тұздардың саны төртеу) болатындығының ықтималдығы қандай?
Шешуі. Тәжірибенің толық тең мүмкіндікті нәтижелері – колодадан үш картаны
алу – 36-дан 3 карта бойынша әртүрлі комбинациялардан тұрады, бұлардың саны келесі
тараудың (1.2.5) формуласымен есептелетін C 336 терулерге тең. Ізделінді A оқиғасына –
алынған үш картадан бір тұз болатындығының нәтижелерінің санын: төртеуден бір тұзды
C 14 әдістерімен, ал кез келген екі картаны қалған 32 картадан C 232 әртүрлі әдістермен
есептейміз.
Сондықтан A оқиғасына қолайлы оқиғалардың жағдайларының саны C 14 C232 мәніне тең.
Ізделінді ықтималдық
1 2
M A C 4 C 32 4 ∙32 ∙31 ∙1 ∙ 2∙ 3
P ( A )=
= 3 =
=0,278.
N
1 ∙1 ∙2 ∙ 36∙ 35 ∙34
C 36
1.3. Геометриялық ықтималдық
Тәжірибенің тең мүмкіндікті ақырлы санды нәтижелерінің негізінде
қарастырылған оқиғалар ықтималдықтарының классикалық анықтамасының
кемшілігі – тәжірибенің ақырсыз жиынды нәтижелері үшін (1.2.10) формуласының қолданылмайтындығы.
Жалпы есеп, осындай жағдай үшін ықтималдықты есептеуге жақындау
моделі келесі түрде тұжырымдалады. Жазықтықта кейбір G аумағын
қарастырамыз. (1.3.1-сурет) және g аумағы G -ге кіреді ( g ϲ G ). G аумағына x
нүктесі қалауынша былай лақтырылады, осы нүкте аумақтың кез келген
19.
орнына тең мүмкіндікті ықтималдықпен түсуі мүмкін, демек, G аумағыныңқандай да бір бөлігіне түсу ықтималдығы, мысалы, g аумағына, осы
аумақтың ауданына пропорционал және оның формасынан, орналасуынан
тәуелсіз.
Сондықтан анықтама бойынша,G аумағына қалауынша лақтырылған
нүктенің ( A оқиғасы) g аумағына түсуінің ықтималдығы тең:
mesg
, ( 1.3 .1 )
mesG
мұнда,mesg - g ϲ G аумағының өлшемі. mesG - G аумағының өлшемі.
P ( A )=
Өлшем ретінде ұзындық, аудан, көлем, бұрыш және т.б. алынулары
мүмкін.
Геометриялық ықтималдықты есептеудің мысалдарын қарастырамыз.
1.3.1-мысал.1200 сектордегі маңызды обьект ӘҚҚ (әуе қорғанысын қорғау) жүйесімен қорғалған. Осы обьектіге кез келген бағытта шабуыл жасайтын ұшақтың ӘҚҚ
жүйесі қорғайтын секторда болуының ықтималдығы қандай?
1.3.1-сурет. Геометриялық ықтималдықты
1.3.2-сурет. ӘҚҚ обьектісінің
есептеу моделі
жүйесі
0
Шешуі. Обьектіні кез келген бағытта шабуылдау 360 дөңгелек секторды құрайды (
G аумағы 1.3.2). 1200 сектор ӘҚҚ жүйесімен қорғалған ( g аумағы). Ұшақтың ӘҚҚ
секторіне ( B оқиғасы) түсуінің ықтималдығы (1.3.1) формуласымен анықталады:
0
120 1
P ( B )=
= .
0
360 3
1.3.2-мысал. A және B екі адам сағат 12-ден кейін бір сағаттың ішінде белгілі
жерде кездесуге келісті. Бірінші келген адам, кездесуді 20 минут күтеді, одан кейін кетеді.
Егер олар бір-бірінен тәуелсіз 12-ден 13-ке дейінгі аралықта кездейсоқ уақытта
келетін болса, A және B адамдарының кездесуінің ықтималдығы (P¿¿ k )¿ қандай?
Шешуі. A -ның келу уақыты (моменті) x арқылы, ал B – y арқылы белгілейміз. A
және B кездесуі үшін
|x− y|≤ 20 ( 1.3.2 )
шарты орындалуы қажетті және жеткілікті. ω элементар оқиғасы ( A және B кездесуі) екі
( x , y ) кездейсоқ параметрлерімен және координаталар ( x , y ) болатын xy жазықтығындағы
нүктемен сипатталады. Жазықтықта элементар нәтижелердің (оқиғалардың) кеңістігін Ω
құрамыз. Бұл – қабырғалары 60 минут болатын квадрат (1.3.3-сурет)). (1.3.2) шарты
орындалады, егер кездейсоқ нүкте ( x , y ) g (штрихталған) аумақта жатса. Оның ауданы ( g
аумағының өлшемі) квадраттың ауданынан екі бұрыштағы үшбұрыштардың аудандарын
алып тастағанға тең:
1
2
S g=SG −2∙ ∙ 40 ;
2
2
2
S g=60 −40 =2000 ;
20.
SG =602=36002000 5
Pk =
=
3600 9
1.3.3-сурет. Нәтижелер кеңістігі және екі адамның
1.3.4-сурет. Бюффон есебі
кездесу аумағы
1.3.3-мысал. Бюффон есебі.
Бір-бірінен L қашықтықта (1.3.4-сурет) жүргізілген параллель түзулермен жазықтық графтарға бөлінген. Жазықтыққа қалауынша ұзындығы e < L ине лақтырылады.
Иненің түзулердің біреуімен қиылысуының ықтималдығы қандай?
Шешуі. Тәжірибенің нәтижесін (иненің түзулерге қарағандағы орны) екі
параметрлермен жазамыз: x - иненің жақын түзуге қарағандағы центрі, φ - иненің түзу
сызықтарға қарағандағы көлбеу бұрышы (1.3.4-сурет). ( x , φ ) параметрлерінің мүмкін
мәндері тең ықтималды және
1
π
0 ≤ x ≤ ,0 ≤ φ ≤ (1.3 .3)
2
2
шамаларымен шектелген екендігі айқын, иненің тек қана жақын түзумен қиылысуын
қарастырғанда (мысалы, сол жағындағы). xφ жазықтықтағы (1.3.5) Ω тік төртбұрышы Ω
элементар оқиғалардың кеңістігін (G аумағы) көрсетеді:
L∙π
SG =
.(1.3 .4)
4
l
Егер ине центрінің абциссасы x ∙ Sinφ - ден кіші болса, онда ине түзуді қияды ( A
2
оқиғасы); Бұған сәйкес келетін барлық нүктелер ωϵΩg аумағында (1.3.5-сурет). g
аумағының ауданы
π /2
l
l
S g= ∫ ∙ Sinφdφ= .(1.3 .5)
2
2
0
Соңында аламыз:
Sg 2 l
P ( A )= = . (1.3 .6 )
S G πL
21.
Сурет 1.3.5. Бюффон есебіндегі жұмыс аумақтары1.4. Оқиғаның шартты жиіліктері және ықтималдығы
A оқиғасының басқа B оқиғасы бар болғандағы шартты жиілігі
P ( A∨B) деп A -мен байланысты, барлық n тәжірибелер жиынтығынсыз
есептелген тек қана A -мен бірге B оқиғасының пайда болғандағы A
¿
оқиғасының жиілігін айтады.
Айталық n – барлық жүргізілген тәжірибелердің саны, mB – B оқиғасы
пайда болғандағы, m AB – А және В оқиғалары бірге пайда болғандағы ( AB)
¿
тәжірибелердің саны. Сонда P ( A∨B) A оқиғасының B оқиғасы бар
болғандағы шартты жиілігі:
¿
P ( A∨B )=
m AB
(1.4 .1)
mB
формуласымен есептеледі.
(1.4.1) алымын және бөлімін тәжірибелер саныn-ге бөлеміз
m AB /n P¿ ( AB )
P ( A∨B )=
= ¿
( 1.4 .2)
mB / n
P (B )
¿
¿
¿
Нәтижесінде, P ( A∨B) шартты жиілікті P ( AB ) және P ( B ) арқылы
¿
өрнектейтін формуланы аламыз. Осы сияқты талдап, P ( A∨B) шартты жиілігі
¿
үшін де мына өрнекті жазамыз:
m AB
,(1.4 .3)
mA
¿
P ( AB)
¿
P ( B∨ A )=
.(1.4 .4)
P( A)
¿
P ( B∨ A )=
Шартты жиілік 0 ≤ P ( A∨B)≤1 шегінде жатады. Шартты жиіліктің
анықтамасына мысал қарастырамыз.
¿
1.4.1-мысал. Транспорт қозғалысын басқарудың n=100 жүйелерінің жұмысына t
уақыт аралығында байқаулар жүргізіледі. Байқаулардың нәтижесінде транзисторлардың
тоқтауынан ( A оқиғасы) m A =10 жүйе істен шыққандығы, автономды қоректендіру
шынжырларының себебінен ( B оқиғасы) mB =14 жүйелер істен шыққандағы, ал осы екі
22.
¿¿
себептерден ( AB оқиғасы) m AB=7 жүйелер істен шыққандығы анықталды. P ( A ) , P ( B )
¿
¿
жиіліктері және P ( AB ), P ( B∨ A ) шартты жиіліктерін анықтаймыз.
¿
¿
¿
¿
Шешуі. P ( A ) және P ( B ) жиіліктерін P ( AB ), P ( B∨ A ) шартты жиіліктерінен
өзгеше шартсыз жиіліктер деп атайды, (1.2.1) формуласымен анықтайды:
m A 10
¿
P ( A)= =
=0,10 ,
n 100
mB 14
¿
P ( B )= =
=0,14.
n 100
(1.4.1) және (1.4.3) формулаларымен шартты жиіліктерді есептейміз:
mA B 7
¿
P ( A∨B )=
= =0,50 ,
m B 14
m
7
P¿ ( B∨ A )= A B = =0,7.
m A 10
¿
n тәжірибелердің
санын шексіз өсіргенде P ( AB )шартты жиілігі
ықтималдық бойынша P( A /B)(1.2.7) шартты ықтималдығына жинақталады.
P (|P¿ ( A∨B )−P ( A∨B )|< ε ) >1−δ , ε > 0 , δ>0.(1.4 .5)
A оқиғасымен байланысты басқа B оқиғасы пайда болғанда есептелген
ықтималдықты P( A∨B) шартты ықтималдығы деп атайды. P( A∨B) шартты
ықтималдығын:
P ( А∨В )=
P ( AB )
(1 . 4 . 6)
P( B)
P ( В∨ А )=
P ( AB )
.(1.4 .7)
P( A)
формуласымен есептейді.
Осы сияқты P(B∨ A) шартты ықтималдығы есептеледі:
Шартты ықтималдық 0 ≤ P (A∨B)≤ 1 арасында жатады. Шартты ықтималдықты анықтау мысалдарын қарастырамыз.
1.4.2-мысал. Үш симметриялы монеталар бір уақытта тегіс үстелдің бетіне
лақтырылады. Оқиғалар қарастырылады: A – бір гербтің пайда болуы, B – тақ санды
гербтердің пайда болуы. P ( А∨В ) шартты ықтималдықты анықтаймыз.
Шешуі. Герб және цифр пайда болғандағы оқиғаларды Г және Ц деп белгілейміз.
Сонда тәжірибелердің нәтижелерінің толық кеңістігі мына түрде жазылады:
Ω={ ГГГ , ГГЦ , ГЦГ , ЦГГ , ГЦЦ , ЦГЦ , ЦЦГ , ЦЦЦ }
Тәжірибенің әртүрлі нәтижелері үш әріппен жазылған, әрқайсысы сәйкесінше
бірінші, екінші, үшінші монеталарды көрсетеді. Тәжірибелердің нәтижесінің жиынтығы
жағдайлар сызбасын құрайды, сондықтан P( AB) және P(B) ықтималдықтары (1.2.10)
формуласымен есептеледі:
m 4
m
3
P ( B )= B = , P ( AB )= AB = .
n 8
n
8
(1.4.6) формуласына сәйкес ізделінді P ( А∨В ) ықтималдығы тең:
3∙ 8 3
P ( А∨В )=
= .
8∙4 4
1.4.3-мысал. 2 ақ және 1 қара шар жатқан урнадан тізбектей бір шардан алады
(1.4.1-сурет). A – ақ шардың пайда болуы, B – қара шардың пайда болу оқиғалары
қарастырылады. P ( A ) , P ( B ) , P ( А∨В ) және P ( В∨ А ) ықтималдықтарын қарастырамыз.
Шешуі. Тәжірибенің нәтижелері жағдайлар сызбасын құрайды. Сондықтан ізделінді ықтималдықтар тең:
23.
21
2
1
P ( A )= , P ( B )= , P ( А∨В )= =1 , P ( В∨ А )= .
3
3
2
2
1.4.1-сурет.Тәжірибенің моделі
Соңында мынаны еске саламыз, (1.4.6), (1.4.7) теңдіктерінің әрқайсысы
ықтималдықтарды көбейту теоремасына (3-тарау) эквивалентті, екі
оқиғалардың көбейтіндісінің ықтималдығы біреуінің ықтималдығы мен
бірінші оқиға орындалғанда есептелген келесісінің шартты ықтималдығының көбейтіндісіне тең, яғни:
P ( AB ) =P ( A ) ∙ P ( В∨А )=P ( B ) ∙ P ( А∨В ) .(1.4 .8)
1.5. Тәуелді және тәуелсіз оқиғалар
A оқиғасы B оқиғасынан тәуелсіз, егер тәжірибенің нәтижесінде B
оқиғасының пайда болуы A оқиғасының пайда болуының ықтималдығын
өзгертпесе, яғни:
P ( А∨В )=P ( A ) .(1.5 .1)
Басқаша айтқанда, егер A оқиғасы B оқиғасынан тәуелсіз болса, онда
P ( А∨В ) шартты ықтималдығы P ( A ) шартсыз ықтималдығына тең.
(1.5.1)-ді (1.4.8)-ге қоямыз:
P ( A ) ∙ P ( В∨ А ) =P ( B ) P ( A ) ,
бұдан
P ( В∨ А )=P ( B ) ,(1.5 .2)
шығады яғни, B оқиғасы A оқиғасынан тәуелді емес.
Демек, егер A оқиғасы B-дан тәуелсіз болса, онда B оқиғасы A -дан
тәуелсіз болатындығы жөніндегі A және B оқиғаларының өзара тәуелсіздік
қасиеті шығады:
P ( A∨В )=P ( A ) , (1.5 .3)
P ( В∨ А )=P ( B ) .
}
Ықтималдықтар теориясында және оның қосымшаларында оқиғалардың тәуелсіздігінің түсінігі маңызды орын алады. Практикадағы есептерде
оқиғалардың тәуелсіздігін тексеру үшін қарапайым интуитивті ойлаулар
пайдаланылады және (1.5.3) теңдігіне сирек оралады. Тәуелсіз оқиғалар үшін
(1.4.8) формуласы, көбейту теоремасын өрнектейтін, қарапайым түрді қабылдайды:
P ( AB ) =P ( A ) P ( B ) . (1.5.4 )
A , B оқиғалары тәуелді деп аталады, егер біреуінің тәжірибе нәтиже-
сінде пайда болуы басқа оқиғаның пайда болуының ықтималдығын өзгертпесе:
P ( A∨В ) ≠ P ( A ) , (1.5 .5)
P ( В∨ А ) ≠ P ( B ) .
}
24.
Тәуелсіз және тәуелді оқиғалардың мысалдарын қарастырамыз.1.5.1-мысал. Қатарынан екі монеталар лақтырылады. Бір монетада гербтің пайда
болуы ( A оқиғасы) және екіншіде цифрдің пайда болуы ( B оқиғасы) – тәуелсіз оқиғалар.
1.5.2-мысал. Урнадан шарларды қайтарумен алу. Бірдей ақ және қара шарлар (6 ақ
және 7 қара) жатқан урнадан, сипауға бір шар алады және оны кері салады. Содан соң
урнадан тағы бір шар алады. Оқиғаларды қарастырамыз: A – бірінші алғандағы ақ шардың
пайда болуы, B – екінші алғандағы ақ шардың пайда болуы. Олардың ықтималдықтары
тең:
6
6
P ( A )= , P ( В∨ А ) = =P ( B ) .
10
10
Берілген мысалда A және B оқиғалары тәуелсіз, өйткені шығарылған шардың
урнаға қайтарылуы алғашқы шарлардың құрамын қалпына келтіреді – 6 ақ және 4 қара
шарлар.
1.5.3-мысал. Урнадан шарларды қайтарусыз алу. 1.5.2-мысалындағы алынған ақ
A
шар ( оқиғасы), бірақ урнаға қайтарылмайды. B оқиғасының ықтималдығы – екінші рет
алынғанда ақ шардың пайда болуы (бірінші алынған шар урнаға қайтарылмау шартынан)
өзгереді, өйткені алты шардың орнында бес шар қалды.
5 6
P ( В∨ А )= ≠
9 10
Демек, бұл мысалда A және B тәуелді, өйткені A -ның пайда болуы B оқиғасының
ықтималдығын өзгертеді.
Егер олардың кез келген Ai оқиғасының ықтималдығы осы оқиғалардың жиынтығынан қандай да бір A j , j≠ i; i , j=1,2 , … , n санды оқиғалар пайда
болғанда өзгермесе, A1 , A 2 ,… , An оқиғалары жиынтықта тәуелсіз немесе
қарапайым тәуелсіз деп аталады.
Басқаша айтқанда, A1 , A 2 ,… , An тәуелсіз, егер кез келген 1 ≤i1 <i 2< ¿ …i k ≤ n
және кез келген k ( 1 ≤ k ≤ n ) үшін
P ( Ai , A i , … , A i ) =P ( A i ) P ( A i ) … P ( A i ) ,(1.5 .6)
1
2
k
1
2
k
яғни оқиғалардың көбейтіндісінің ықтималдығы осы оқиғалардың ықтималдықтарының көбейтіндісіне тең болса.
Мысалы, n=3 болғандағы (1.5.6) теңдігінің түрі:
P ( A 1 A 2 )=P ( A1 ) P ( A 2 ) ,
P ( A 1 A 3 )=P ( A1 ) P ( A 3 ) ,
(1.5 .7)
P ( A 2 A 3 )=P ( A2 ) P ( A 3 ) ,
P ( A 1 A 2 A3 ) =P ( A 1 ) P ( A2 ) P ( A3 ) .
Ескертеміз, оқиғалардың қос-қостан тәуелсіздігі жиынтықтағы
тәуелсіздігіне кепілдік бермейді. A1 , A 2 ,… , An оқиғаларының тәуелсіздігінен,
осы оқиғалардың кез келгені қалғандарының кез келген комбинациясынан
тәуелсіз болып шығатындығын көрсетуге болады.
Мысалы, өрнектер дұрыс:
P ( A 2∨A 1 )=P ( A 2) ,
P ( A 3∨ A 1 A2 ) =P ( A 3 ) ,
P ( A 4∨ A1 ∙ A 2 A3 ) =P ( A 4 ) , (1 .5 . 8)
………… ……
P ( A n∨ A1 A2 A 3 … A n−1 )=P ( A n ) .
25.
1.5.4-мысал. Әрбір атуда көздей отырып, атқыш нысанаға атысты біртіндеп атуменжүргізеді. A1 , A 2 ,… , An оқиғаларын қарастырамыз, мұнда, Ai ( i=1,2 , … ,n ) i -інші атқандағы нысанаға тигізу. A1 , A 2 ,… , An оқиғалары тәуелсіз, өйткені атулардың бірінің нәтижелері басқа атулардың нысанаға тиюінің ықтималдығына әсер етпейді (тәуелсіз атулар).
2-ТАРАУ
Ықтималдылық есептеріндегі комбинаторика
2.1. Ықтималдылық есептердің комбинаторлық сипаты
Комбинаторика – дискреттік математиканың бір бөлімі, белгілі
шарттарға бағынатын табиғи еркін обьектілерінің алмастыруларын және
комбинацияларын оқытатын ғылым.
Жиындар теориясынан қарағанда комбинаторика ақырлы жиындардың әртүрлі жиыншаларын,олардың бірігулерімен және қиылысуларымен
құрылу әдістерімен істес, сол сияқты осындай жиыншаларды реттеу әдістерін жасайды.
Әдістемелік тұрғыда комбинаторика ықтималдықтар теориясына
кіріспе түрінде қарастырылады, өйткені ықтималдылық есептерді шешкенде
кеңінен қолданылады [9]. Ереже секілді, классикалық сызба бойынша
ақырлы санды тең мүмкіндікті нәтижелермен (1.2.10) есебін шешу N
жағдайларының жалпы санын және кейбір A оқиғасына қолайлы M A
жағдайларының санын есептеу үшін комбинаторика әдістерін қолдануға
алып келеді:
P ( A )=
MA
.( 2.1.1)
N
Ықтималдықтар теориясынан басқа, комбинаторика ғылым мен
техниканың көптеген салаларында: дербес жағдайда, ақпараттық теорияда,
кодтауда, статистикалық физикада, графтар теориясында, эксперименттерді
жоспарлауда, бағдарламалар теориясында, генетикада, биологияда қолданыс
тапты.
Оларды шешу үшін комбинаторлық әдістердің қажеттілігін растайтын
бірнеше мысалдарды қарастырамыз.
2.1.1-мысал. Ойын сүйегі екі рет қатарынан лақтырылады. Бірінші және екінші
лақтыруларда ( A оқиғасы) ұпайлардың бір және сондай сандардан пайда болу
ықтималдығы есептеледі.
Шешу жоспары. Әрқайсысы 1- және 2-позицияда 1-ден 6-ға дейінгі екі таңбалы
сандардан құралған (1,1), (1,2), ..., (3,6), ..., (6,6), яғни 1- және 2-сүйектерге түсетін цифрлардың барлық мүмкін комбинацияларын қарастыру қажетті жағдайлардың жалпы сандарын (тәжірибенің нәтижелерін) анықтау үшін A оқиғасына қолайлы оқиғалардың жағдайларының саны, екі бірдей цифрлардан тұратын, яғни (1,1), (2,2), ..., (6,6) екі таңбалы
сандарының санына тең.
2.1.2-мысал. Бірдей 6 ақ және 4 қара шарлар орналасқан урнадан қалауынша 4 шар
алады. Комбинациялар ықтималдығын анықта: 2 ақ және 2 қара шар (А оқиғасы).
Шешу жоспары. Барлық жағдайлардың сандарын анықтау үшін (тәжірибенің
нәтижелерін), ең болмағанда, бір шармен өзгешеленетін 10-нан 4 шар бойынша барлық
26.
мүмкін комбинацияларды қарастыру керек, яғни 1-ден 10-ға дейін барлық шарларқайтадан нөмірленген деп ұйғарып, төрттікті қарастыру керек: (1,2,3,4), (1,2,3,5), ...,
(5,6,7,8), ..., (7,8,9,10). А оқиғасына қолайлы жағдайлардың саны, 2 әртүрлі ақ шарлардың,
2 әртүрлі қара шарлардың комбинацияларының сандарына тең. Егер, мысалы, ақ шарлардың нөмірлері 1...6, ал қара шарлар нөмірлері 7...10 болса, онда (1,2,7,8; 1,3,7,8; ...;
5,6,9,10) комбинацияларын қарастыру керек. Мысалдарда келтірілген комбинацияларының сандарын есептеу тәсілдері төменде қарастырылады, ал есептер тараудың
соңында шешіледі.
2.2. Элементтер жиынынан таңдама
Ықтималдықтар есептерін шешуге қолданылатын комбинаториканың
әдістерін баяндау «жиындардың элементтерінен таңдама» түсінігі негізінде
жүргізіледі, ал бұл барлық комбинаторлық әдістерді бір позициядан
қарастыруға мүмкіндік береді.
X1 , X2 , … , Xk
Айталық,
жиындарының k
жиыны сәйкесінше
N 1=N ( X 1), N 2=N ( X 2) , … , N k =N ( X k ) элементтері сандарымен берілсін.
Келесі түрдегі
{ x (1i ) , x(2)j , … , x(k)ν } ,(2.2 .1)
мұндағы x(1)
i ∈ X 1 , i=1 , … , N 1,
x(2)
j ∈ X 2 , j=1 ,… , N 2,
… … … … … …
x(k)
ν ∈ X k , ν=1 , … , N k ,
X 1 , X 2 , … , X k жиындарының элементтерінің жиынынk көлемді ¿-таңдама) деп
атаймыз.
2.2.1-сурет. k -таңдаманың қалыптасу процедурасы
Жиындардың элементтерінен таңдаманы қалыптастыру процедурасын
мысалда түсіндіреміз.Айталық, сәйкесінше қайта нөмірленген жәшіктерге
(2.2.1-сурет) X 1 , X 2 , … , X k жиындарының элементтері салынсын.
1-жәшіктен x(1)
i , i=1 ,… , N 1элементі шығарылады,
2-жәшіктен – x(2)
j элементі, j=1 ,… , N 2 , … ,
k -ші жәшіктен x(k)
ν , ν =1 ,… , N k , элементі шығарылады.
(2 )
(k)
(2.2.1) таңдамасының x(1)
элементтері оның компонент-тері
i , x j , … , xν
деп аталады.
27.
Егер таңдаманың компоненттері X 1 , X 2 , … , X k жиындарынан, олардыңтаңдауының ретімен орналасса (сызыққа), онда ондай таңдама реттелген
деп аталады және
(2)
(k)
Bl=( x(1)
i , x j , … , x ν ) , l=1 , … , m(2.2.2)
деп белгіленеді.
Егер таңдаманың компоненттері ретсіз орналасса, онда ондай таңдама
ретсіз деп аталады және
Bξ = [ x i , x j ,… , x ν ] , ξ=1 , … , p (2.2.3)
(1)
(2)
(k )
деп белгіленеді.
Кей жағдайларда X 1 , X 2 , … , X k барлық жиындары тең болуы мүмкін, яғни
бірдей элементтерден тұрады. Сонда k -таңдамаларды құру процедурасы бір
және сол жәшіктен компонентті таңдау секілді, олардың тиістілік жазылуы
(нөмірлері) және кері қайтуы (немесе қайтымсыз) көрсетіледі.
Мысалы, телефон нөмірі 129-64-75 – реттелген таңдама, кодталған
құлыптағы цифрды теру 73385 – реттелген таңдама, спортлотодағы (36-дан 5)
ұтыстардың нөмірлерін теру: 5, 10, 13, 21, 32 – ретсіз таңдама.
2.3. Реттелген таңдамалар (орналастырулар)
Орналастырулардың санын есептеудің жалпы ережесі
Реттелген
(1)
i
(2)
(k)
Bl=( x , x j , … , x ν ) , l=1 , … , m,(2.3.1)
(2)
X 1 жиынынан x(1)
i , i=1 ,… , N 1элементін, X 2 жиынынан x j , j=1 , … , N 2 элементін,
соңында X k жиынынан x(k)
ν , ν =1 ,… , N k элементін таңдау жолымен алынған k -
таңдаманы (орналастыруды) қарастырамыз.
Сондай { Bl } таңдамаларының жиыны X 1 , X 2 , … , X k k жиындарының тіке
(декарттық) көбейтіндісі деп аталады және
{ Bl }=X 1 × X 2 ×… × X k ,l=1, … , m(2.3 .2)
деп белгіленеді.
Осындай процедураның нәтижесінде элементтері қайталанбайтын
k – таңдаманы (орналастыруды) аламыз.
2.3.1-мысал. Айталық, A={ a , b } , B={ c , d , e } .Сонда A , B жиындарынан орналас-тыру
(2-таңдама)
{ Bl }=A × B=¿
¿ { ( a ,c ) , ( a , d ) , ( a ,e ) , ( b , c ) , ( b , d ) , ( b , e ) , ( c , a ) , ( d , a ) , ( e , a ) , ( c , b ) , ( d , b ) , ( e ,b ) }
түрінде болады.
Егер X 1 , X 2 , … , X k жиындары бірдей және сондай элементтерден тұрса, онда k –
таңдамалардың { Bl } жиыны
X 1 =X 2=…=X k =X
бірдей жиындарының тіке көбейтіндісі болады және
k
× X × …× X =X ,l=1 ,… , m ( 2.3.3 )
{ Bl }=X
⏟
k рет
деп белгіленеді.
28.
Бұл жағдайда бір және сондай X жиынынан N ( X)=N элементтерімен элементтерді таңдады деп есептеуге болады.Әрбір таңдалған элемент белгіленеді, содан соң кейінқайтарылады. Қайтарылған элемент қайтадан алынуы мүмкін болғандықтан, алынған
реттелген таңдау қайталанатын элементтермен орналастыру деп аталады.
2.3.2-мысал. Айталық, X ={ a , b }. Сонда екі элементті таңдамалар жиыны тең
2
X ={ ( a , a ) ,(a , b) , ( b , a ) , ( b , b ) }
Реттелген таңдамалар санын есептейтін негізгі екі ережені қарастырамыз –
көбейтудің ережесі және қосудың ережесі.
Реттелгенk – таңдамаларды құру үшін, берілген қасиетті қанағаттандыратын, x i(1)
элементті X 1 жиынынан N 1 тәсілдермен (осы жиынның N 1 элементі бойынша), x j(2 )
(k)
элементті X 2 жиыннан N 2 тәсілдермен және с.с., соңында, x γ элементті X k жиыннан – N k
тәсілдермен таңдауға болады. Сонда, берілген қасиетті иеленетін N ( k) таңдамалардың
саныk , N 1 , N 2 , … , N k сандарының көбейтіндісіне тең:
k
N ( k)=N 1 N 2 … N k =∏ N i .(2.3 .4)
i=1
Алынған (2.3.4) нәтижесі көбейтудің ережесі. Егер, дербес жағдайда,
X 1 =X 2=…=X k =X және N 1=N 2 =…=N k =N , онда көбейтудің ережесі (2.3.4):
k
N ( k ) =N (2.3 .5)
болып жазылады.
2.3.3-мысал. Жеті таңбалы телефон нөмірлерінің мүмкін сандары N (7)-ні анықтаймыз.
Шешуі. Телефонның нөмірлері болатын жеті таңбалы ізделінді сан X 1 ={ 1,2, … , 9 } ,
N 1=9 және бірдей алты X 2 =X 3=…=X ={ 0,1,2 , … , 9 } , N i=10 (i=2,3 , … ,7) жиындарынан
таңдалған реттелген 7-таңдамалар санына тең. (2.3.4), (2.3.5) көбейтудің ережелеріне
сәйкес
6
N (7)=N 1 N 2 … N 7=9 ∙ 10
2.3.4-мысал. Үш әріптерден және үш цифрлардан тұратын, Ресей Федерациясының
бір өлкесіндегі автомобильдердің нөмірлерінің мүмкін санын анықтаймыз, мысалы,
төменде кескінделген
К 275 МН
77
RUS
Шешуі. Автомобильдер нөмірлерінің ізделінді саны екі типті X 1 =X 2= X 3=¿
¿ { 0,1,2 , … , 9 } , N 1 =N 2=N 3=10 және X 4= X 5=X 6 ={ А , Б , В , … , Я } жиындарынан Е, Й, Ь, Ъ,
Ы әріптерін шығарған соң, реттелген 6-таңдамалардың санына тең, N 4 =N 5=¿ N 6 =28.
Көбейтудің ережесі (2.3.4)-ке сәйкес, аламыз:
3
3
N (6)=N 1 N 2 … N 6=10 ∙ 28 =21952000.
Барлық мүмкін таңдамалардың жиыны, қандай да қиылыспайтын
әртүрлі кластар – B j , j=1 , … , n жиыншалары түрінде көрсетілсе, бұл жағдайда
қосындының ережесі қолданылады (2.3.1-сурет).
29.
2.3.1-сурет. Қиылыспайтын таңдамалар кластарының жиыныОсы жағдайда таңдамалардың жалпы саны әртүрлі кластардағы
таңдамалардың сандарының қосындысына тең:
n
N=N 1+ N 2+ N 3 + …+ N n=∑ N j .(2.3.6)
j=1
Осы формула – қосындының ережесін анықтайтын формула. Әр түрлі
кластардағы
таңдамалардың N 1 + N 2 +…+ N n сандары
сәйкесінше
(2.3.4)
көбейтудің ережесімен анықталады.
2.3.5-мысал. Корабльдің төрт әртүрлі белгі жалауларынан қанша әртүрлі белгілерді
құруға болатынын анықтаймыз.
Шешуі. Әртүрлі белгілерді құрудың варианттарының жиынын төрт қиылыспайтын
жиыншаға бөлуге болады:
B1 – бір жалаудан құрылған белгілердің жиыны;
B2 – екі жалаудан құрылған белгілердің жиыны;
B3 – үш жалаудан құрылған белгілердің жиыны;
B4 – төрт жалаудан құрылған белгілердің жиыны.
Төрт жалаудан құрылған белгілердің нұсқаларының жалпы саны мынаған тең
(2.3.6):
N=N 1+ N 2+ N 3 + N 4 ,
мұнда, N 1=4 бір жалаудан белгілердің нұсқасы,
N 2=4 ∙ 3=12 екі жалаудан белгілердің нұсқасы,
N 3=4 ∙ 3∙ 2=24 үш жалаудан белгілердің нұсқасы,
N 4 =4 ∙3 ∙ 2∙ 1=24 төрт жалаудан белгілердің нұсқасы.
Сонымен, нәтижесінде аламыз:
N=4+ 12+ 24+24=64 (белгілер нұсқасы).
N k сандарын есептегенде (2.3.4) көбейтудің ережесін қолдандық.
Мысалы, N 3 санын есептегенде үш жалаудан белгіні құру үшін бірінші жалауды қалған
төрт жалаудың кез келгенінен таңдауға болады. Екінші жалау, қалған үшеудің біреуі, ал
үшіншісі қалған екеудің біреуі болуы мүмкін. Бұдан нәтиже: N 3=4 ∙ 3∙ 2=24 .
Қайталанатын орналастырулар
Реттелген k-таңдама
(1)
i
(k)
Bl=( x , x (2)
j , … , x ν ) , l=1 , … , g ; i , j , … , ν=1 , … , n ,(2.3 .7)
бір және сол n-жиынның элементтерінен
X ={ x 1 , x 2 , … , x n } (2.3 .8)
құрылған, n элементтерденk элементтері
бойынша
қайталанатын
орналастырулар деп аталады.
Бұл таңдаманың компоненттері теңесуі мүмкін. (2.3.7)-дегі жоғарғы
индекс X жиынына оралудың нөмірін көрсетеді.
Осындай екі таңдамалар әртүрлі болады, егер олар тең емес компоненттердің ретімен немесе олардың құрамымен өзгешеленсе.
Қайталанатын орналастырулардың саны Akn деп белгіленеді ( A әрпі –
arrangement – орналастыру сөзінің басы) және (2.3.4), (2.3.5) көбейтудің
ережесі бойынша анықталады N 1=N 2 =…=N k =n:
k
k
An =n .(2.3 .9)
30.
Қайталанатын орналастырулардың сандарын есептеу мысалдарынқарастырамыз.
2.3.6-мысал. Қайталанатын орналастырулардың құрамы және саны. X ={ A , B , C ,
D , E } , n=5жиынының элементтерінен қайталанатын орналастыруларды (реттелген
таңдамалар) 3 элемент бойынша әрқайсысында құрамыз және олардың санын анықтаймыз.
Шешуі. (2.3.9) қолданып, X жиынының бес элементтерінен 3 элемент бойынша
қайталанатын орналастыруларды былай құрамыз:
A35 =53=125.
Осы таңдамалар бір-бірінен компоненттер құрамымен, немесе олардың ретімен
өзгешеленеді
B= { ( A , A , A ) ,( A , A , B),( A , A , C),(A , A , D) ,(A , A , E),( A , B , A),( A , B , B),(B , B , B) ,… ,( E , E , E) } .
2.3.7-мысал. Сандарды құру. X ={ 1 ,2 , 3 , 4 , 5 , 6 ,7 ,8 , 9 }цифрларының жиынынан,
егер цифрлар қайталанатын болса, қанша төрт таңбалы сандарды құруға болатынын
анықтаймыз.
Шешуі. 9 элементтерден 4 элемент бойынша қайталанатын орналастырулардың
санына төрт таңбалы сандардың саны тең:
4
4
A9 =9 =6561 .
2.3.8-мысал. Құпиялық құлпының құрылымы, әрқайсысына 12 әріп жазылған
(А, Б, В, ..., Л, М) бес дөңгелектен тұрады. Тек сол жағдайда, егер код құрылымында
таңдалған (құлыптың «терезесіндегі» саңылауда оқылады) 5 әріптен құрылған «сөз»
«кілттік» сөзбен, мысалы «ВИЛКА» сөзімен сәйкес келсе, құлып ашылады. Құлыптың
кодын жинаудың нұсқаларының санын анықтаймыз.
Шешуі. «Сөздің» жалпы саны 12 әріптерден 5 әріптер бойынша қайталанатын
орналастырулардың санына тең:
A512=125=248832.
Олардың тек қана біреуі «кілттік» сөз! Егер бір вариантты теруге 10 секунд
жұмсалса, онда 248832 нұсқаларды қайта теруге шығындалатын уақыт
с
T =248832 ∙10 с : 3600
=691,2 са ғ ≅ 29 к ү н .
са ғ
Қайталанбайтын орналастырулар
(1)
(2)
(k)
Bl=( xi , x j , … , x ν ) , l=1 , … , g ,(2.3 .10)
i=1 , … , n , j=1 , … ,(n−1) , … , ν=1−k +1 ,
X ={ x 1 , x 2 , … , x n } ,(2.3 .11)
компоненттері бір және сол жиынның элементтері және барлық компоненттері әртүрлі болатын реттелген k – таңдамасы n элементтерден k
элементтері бойынша ( k < n ) қайталанбайтын орналастырулар деп аталады.
Егер олар бір-бірінен ең болмағанда бір компонентімен немесе бірдей
және сондай компоненттердің ретімен (орналасуымен) өзгешеленсе, сондай
екі таңдамалар әртүрлі.
Қайталанбайтын орналастырулар саны Akn деп белгіленеді және
N 1=n, N 2=n−1 , N 3=n−2 ,… , N k =n−k +1 болғандағы (2.3.4) көбейтудің ережесіне
сәйкес анықталады:
k
An =n ( n−1 )( n−2 ) … ( n−k + 1 ) .(2.3 .12)
31.
Элементтері қайталанбайтын орналастыруларды қалыптастыру тәсілдері (реттелгенk – таңдамалар) келесі түрде: бірінші x i(1) компонентасы Xжиынынан n тәсілдермен, екінші x j(2 ) – (n−1) тәсілдермен, ..., k -шы
компонента x γ(k) – (n−k +1) тәсілдермен, әрбір таңдаудан кейін қалған-дарынан
– элементтердің саны бойынша орындалады.
Akn үшін қолайлы формуланы алу үшін (2.3.12) өрнегін n !-ға дейін
толықтыратын
( n−k ) !=( n−k ) (n−k −1) … 3 ∙2 ∙1 ,(2.3 .13)
шамасына көбейтеміз және бөлеміз.
Сонда соңында аламыз:
k
An =
n!
.(2.3 .14)
( n−k ) !
Қайталанбайтын
орналастырулардың
мысалдарын қарастырамыз.
сандарын
анықтаудың
2.3.9-мысал. Қайталанбайтын орналастырулардың құрамы және саны.
X ={ A , B , C , D , E } ,n=5
5 элементтерден 3 элемент бойынша орналастыруларды құрамыз және олардың санын
анықтаймыз.
Шешуі. 5 элементті X жиынынан (2.3.12) көбейтіндісін құруға болады.
3
A5 =5∙ 4 ∙3=60 ,
қайталанбайтын, 3 элементтен тұратын орналастырулардың санына тең.
Осы таңдамалар бір-бірімен компоненттер құрамымен немесе олардың ретімен
өзгешеленуі мүмкін, бірақ әртүрлі таңдамаларда элементтер қайталанбайды.
Оларды қайта санайық:
B= { ( A , B , C ) ,( A , B , D) ,( A , B , E) ,(B , A , C),(B ,C , A), … ,(E , D ,C ) }
2.3.10-мысал. Сандарды құру.
1, 2, 3, 4, 5 цифрларынан, егер цифрлар қайталанбаса, қанша төрт таңбалы
сандарды құруға болатынын анықтаймыз.
Шешуі. Төрт таңбалы сандардың саны 5 элементтерден 4 элемент бойынша қайталаусыз орналастырулардың санына тең:
4
A5 =5 ∙ 4 ∙ 3 ∙2=120 (сандар).
2.3.11-мысал. Хоккей турнирінің жеңімпаздары.
Егер 12 ойын командасының ойнау деңгейі және ойыншылар құрамы тең болса деп
ұйғарсақ, онда командалар арасындағы алтын, күміс, қола медальдарды үлестірудің
қанша әдістері болатындығын анықтаймыз.
Шешуі. Есеп командалардың үштігінің, бір-бірінен құрамымен немесе орындардың
үлестірілу ретімен өзгешеленетін 12 элементтен үш таңдамалар бойынша, санын
анықтауға тіреледі. Бұл – қайталанбайтын орналастырулар санына тең:
3
A12=12 ∙11 ∙10=1320 (тәсілдер).
Қайталанбайтын алмастырулар
жиынының барлық элементтерінен, яғни n элементтерден n
бойынша қайталанбайтын орналастыруларды қайталанбайтын алмастырулар (немесе жай алмастырулар) деп атайды.
Олардың саны Pn деп белгіленеді және (2.3.15) өрнегімен анықталады:
X
n
Pn= A n=n ( n−1 )( n−2 ) … 3 ∙2 ∙1=n ! ,
32.
Pn=n! .(2.3.15)Екі алмастырулар әр түрлі, егер компоненттердің тек қана ретімен
өзгеленсе,өйткені,олардың құрамына алғашқы X (2.3.11) жиынының барлықn
элементтері кіреді.
X жиыныныңn элементтерінен құрылған алмастыруларды қарастырамыз.
2.3.12-мысал. Алмастырулардың саны және құрамы. X ={ A , B , C , D , E } ,n=5
жиынының элементтерінен барлық мүмкін алмастыруларды құрамыз (бес элементтерден
бес элемент бойынша қайталанбайтын алмастырулар) және олардың санын анықтаймыз.
Шешуі. A , B , C , D , E бес элементтерден тұратын алмастырулардың саны тең:
P5=5 !=1 ∙2 ∙3 ∙ 4 ∙ 5=120.
Сәйкес алмастырулар:
{ P5 }={ ( A , B , C , D , E ) , ( B , A ,C , D , E ) , ( B , C , A , D , E ) ,
( B ,C , A , E , D ) , (C , A , B , D , E ) , … , ( E , D , C , B , A ) }
түрінде жазылады.
2.3.13-мысал. Сөредегі кітаптарды алмастыру. Кітап сөресіндегі 4 әртүрлі
кітаптарды қанша әдіспен алмастыруға болады?
Шешуі. Төрт кітапты алмастырулар саны төрт элементтерден құрылған алмастырулардың санына тең.
P4 =4 !=1 ∙ 2∙ 3 ∙ 4=24 (тәсіл).
9-қосымшада n ! n=1 ,… , 30 үшін берілген. Соңында, 0 !=1 деп қабылданғанын
ескертеміз. Бұған негіз болатын факториалдың қасиеті
n !=n ( n−1 ) !.
Жоғарыда келтірілген өрнек n>1 үшін дұрыс. Сонда 0 ! мәнін, n=1 болғанда
анықтауға болады. Демек, мына қатынас
1 !=1 ∙ 0 !
орындалуға тиіс.
Бірақ бұл үшін 0 !=1 деп есептеу қажет.
Қайталанатын алмастырулар
Ең болмағанда екі компоненттері бірдей болатын алмастырулар
қайталанатын алмастырулар деп аталады.
X жиынының n элементтерінен алмастырулар құрылсын,
Айталық, ~
олардың арасында бірдей элементтер бар, мысалы, A элементтері n1 , B
элементтері n2 , C элементтері n3 , … , L элементтері n k, сонда элементтердің
санының қосындысы тең:
n1 +n 2+n 3+ …+nk =n .(2.3 .16)
X жиынының n элементтерінен құрылған
Жалпы саны n ! болатын, ~
мүмкін алмастырулардың бір түрі, мысалы, мынадай түрде болуы мүмкін:
n
⏟ ⏟ ⏟ ⏟)
(⏞
A , A , ... , A , B , B , … , B , C ,C ,… , C ,… , L , … , L .(2 .3 . 17)
n1
n2
n3
nk
(2.3.17) алмастыру – қайталанбалы алмастырулар. Қайталанбалы
алмастырулар саны
P ( n1 , n2 , … , nk )
символымен белгіленеді.
33.
A , A ,... , A n1 !Оны
анықтағанда
мынаны
ескереміз,
бірдей
n
!
компоненттерін алмастырып 1 тәсілмен, біз жаңа алмастыруларды алмаймыз, бұдан, алмастырулардың жалпы n ! санын n1 ! есе кеміту керек екендігі
шығады. Осы сияқты, B , B , … , B2 −n2 бірдей компоненттерін n2 ! тәсілмен
алмастырып, біз тағы да жаңа алмастыруларды алмаймыз, бұдан тағы да
алмастырулардың жалпы n ! санын n2 ! есе кеміту керек болады. Әрі қарай осы
тұрғыдан талдай отырып, келесі нәтижені аламыз:
n!
.(2.3 .18)
n1 ! n 2 ! … n k !
2.3.14-мысал. АВИАЦИЯ сөзін құрайтын әріптерден қанша жеті әріпті әртүрлі
«сөз» құруға болады?
Шешуі. АВИАЦИЯ сөзінде екі «А» ( n 1=2 ), екі «И» (n2 =2) бір-бірден «В», «И», «Я»
(n3 =n4 =n5=1 ) әріптері бар. Әріптердің жалпы саны n=7. Жеті әріптен алмастырулардың
жалпы саны тең:
P7=7 !=1 ∙2 ∙ 3∙ 4 ∙5 ∙ 6 ∙7=5040.
Бірақ, «А» және «И» бірдей әріптерді алмастыру жаңа сөзді бермейтінін ескеріп
аламыз:
7!
5040
P ( 2 ,2 , 1, 1 ,1 )=
=
=1260.
2 ! 2 !1! 1 ! 1!
4
P ( n1 , n2 , … , nk ) =
2.4. Реттелмеген таңдамалар (терулер)
Қайталанбайтын терулер
Реттелмеген k – (2.2.3) таңдамасы
(2)
(k)
Bξ =[ x (1)
i , x j , … , x ν ] , ξ=1, … , p ; i, j , ν=1 , … , n ;i ≠ j ≠ … ν ,(2.4 .1)
n элементтерден k элементтері бойынша ( k ≤ n ) қайталанбайтын терулер
немесе жай терулер деп аталады, егер элементтері бір және сондай
X ={ x 1 , x 2 , … , x n } (2.4 .2)
жиынының элементтерінен құрылса.
Ондай таңдаманың барлық компоненттері әртүрлі, ал олардың реті
мәнді болмайды.
Егер олар ең болмағанда бір компонентпен өзгешеленсе, сондай екі
таңдамалар әртүрлі.
Егер олардың компоненттері бірдей болса, сондай екі таңдамалар
әртүрлі.
Терулердің мысалдары:
1. «Спортлото» картасын толтыру үшін 36 цифрдан 5 цифрды таңдау (сандардың өзі
мағыналы, бірақ олардың реті емес).
2. Футбол командасының құрамына 40 үміткерден он сегіз ойыншыны таңдау
(ойыншылардың кандидатурасы мағыналы, бірақ оларды таңдау реті емес).
3. Бау-бақша серіктестігінің 50 мүшесінен тексеру комиссиясының мүшелігіне 3
мүшені таңдау. (адамдардың өздері мағыналы, оларды таңдаудың реті емес)
n элементтерден k элементтер ( k ≤ n ) бойынша терулерді C kn деп белгілейді.
n элементтерден k элементтері бойынша C kn терулерінің санын есептеу
үшін (2.3.14) формуласы қолданылады.
34.
Нақтысында, C kn санына тең болатын n-нен k элементтері бойыншабарлық терулерді құрамыз, ал содан кейін әрбір k компонентті терулерден
барлық мүмкін алмастыруларды жасаймыз, бұлардың саны k !. Элементтері
қайталанбайтын реттелген таңдамалардың жиынын – k элементтері бойынша
n элементтерден орналастыруларды аламыз. Сонымен, былай жазамыз:
k
k
An =Cn k ! ,(2.4 .3)
(2.3.14) өрнегін ескеріп, бұдан Ank үшін мынаны аламыз:
A kn
n!
C = =
.(2.4 .4)
k ! k ! ( n−k ) !
k
n
(2.3.12) түрдегі басқа Akn жазылуын ескеріп, практикалық есептеулерде
тиімді C kn үшін өрнекті аламыз:
n ( n−1 ) ( n−2 ) …(n−k +1)
.(2.4 .5)
k!
Ескертеміз, C kn үшін алынған (2.4.4) формуласы құрамына бір типті k
элементтер және басқа типтегі ( n−k ) элементтер кіретін n элементтерден
k
C n=
қайталанатын алмастырулар санының (2.3.18) формуласымен теңеседі
(мысалы, k” бірлік” және (n-k)” нөлдер” ).
Нақтысында,
P ( k , n−k )=
n!
=C kn .
k ! ( n−k ) !
(2.4.6)
Терулердің санын есептейтін мысалдарды қарастырамыз.
2.4.1-мысал. Урнадан шарларды таңдау. Арасында әртүрлі түсті шарлар болуы
мүмкін, 10 бірдей сипауға болатын шарлар жатқан урнадан қалауынша 4 шарды алады. 10
әртүрлі түсті шарлардан төртеуін таңдаудың қанша тәсілдері болады, егер сондай
таңдамалар ретімен емес, тек қана құрамымен өзгешеленсе (терулер)?
Шешуі. 10 әртүрлі шардан 4 шарларды таңдаудың тәсілдері 10 шарлардан 4 шар
бойынша реттелмеген таңдаулардың (терулер) санына тең:
10 ∙ 9 ∙8 ∙ 7
4
C 10=
=210 (тәсілдермен).
1 ∙ 2∙ 3 ∙ 4
2.4.2-мысал. Комиссияның мүшелерін таңдау. Бөлімде 8 қызметкерлер бар, оның
бесеуін инвентарь есеп жүргізу комиссиясының мүшелері етіп жіберуге тиіс. Комиссияны
қанша тәсілмен таңдауға болады?
Шешуі. Комиссияны таңдаудың тәсілдерінің саны 8 – ден 5 элементтер бойынша
(2.4.5) терулердің санына тең (қайталанбайтын ретсіз (реттелмеген) таңдаулар):
8 ∙7 ∙ 6 ∙5 ∙ 4
5
C 8=
=56(тәсілдер).
1 ∙2 ∙3 ∙ 4 ∙5
Терулердің қасиеттері
Комбинаториканың тәжірибедегі есептерін шешуді жеңілдететін терулердің бірқатар тамаша қасиеттері бар. Осы қасиеттерді қарастырамыз.
1-қасиет. n элементтерден бір элемент бойынша терулердің саны n-ге
тең:
C 1n=n .(2.4 .7)
35.
Дәлелдеуі: Мұнда және әрі қарай дәлелдеу үшін (2.4.4) формуласықолданылады, яғни
C 1n=
1 ∙ 2∙ 3 … ( n−1 ) ∙ n
n!
=
=n.
1! ( n−1 ) !
1 ∙2 ∙ 3 … ( n−1 )
2-қасиет. n элементтерде n бойынша терулердің саны бірге тең:
C nn=1.(2.4 .8)
Дәлелдеуі: 0 !=1 екенін ескеріп, аламыз:
n!
=1.
n! ( n−n )
3-қасиет. n элементтерден k бойынша терулердің саны n элементтерден ( n−k ) элементтер бойынша терулердің санына тең:
k
n−k
C n=C n . (2.4 .9)
3
Мысалы, C 810=C210 ,C 97
100 =C 100 және т.б.
n
C n=
Дәлелдеуі:
C n−k
n =
n!
n!
=
=C kn .
( n−k ) ! [ n−( n−k ) ] ! k ! ( n−k ) !
4-қасиет. Паскаль ережесі.n элементтерден k бойынша терулердің
саны ( n−1 ) элементтерден сәйкесінше k бойынша және ( k −1 ) элементтері
бойынша терулердің сандарының қосындысына тең:
k
k−1
k
C n=C n−1+C n−1 , k=1 , … , n .(2.4 .10)
Дәлелдеуі:
( n−1 ) !
( n−1 ) !
+
.
( k −1 ) ! ( n−k ) ! k ! ( n−k−1 ) !
Теңдіктің оң жағындағы өрнекті k ! ( n−k ) ! ортақ бөліміне келтіреміз, ол
үшін бірінші қосылғышты k -ға, ал екіншісін ( n−k ) -ға көбейтеміз және
k
C k−1
n−1+C n−1=
бөлеміз:
k ( n−1 ) !
( n−k )( n−1 ) !
( n−1 ) ! ( k+ n−k )
+
=
=¿
k ! ( n−k )
[ ( k−1 ) ! ∙ k ] ( n−k ) ! k ! [ ( n−k −1 ) ! ( n−k ) ]
¿
( n−1 ) !n
n!
=
=Cnk .
k ! ( n−k ) ! k ! ( n−k ) !
«Паскаль ережесі» деп аталатын (2.4.10) өрнегі Ньютон биномындағы
жіктелуде биномиалды коэффициенттер деп аталатын әртүрлі n және m
мәндері үшін C mn (терулер) сандарын жеңіл есептеуге мүмкіндік береді.
m
C n сандарының Паскаль ережесі (2.4.10) бойынша құрылған («арифметикалық үшбұрыш») 3-кестені қарастырамыз. Кестенің жолдары n
мәндеріне, ал бағандары m мәндеріне сәйкес келеді. Бірінші және соңғы
жолдарының элементтері бірге тең, өйткені
0
n
C n=C n=1.
3-кесте
Терулердің саны
36.
n0
1
2
3
4
5
…
n-1
n
k
0
1
1
1
1
1
1
…
C 0n−1
0
Cn
1
2
3
4
5
1
2
3
4
5
1
3
6
10
1
4
10
1
5
1
C 1n−1
1
Cn
C 2n−1
2
Cn
C 3n−1
3
Cn
C 4n−1
4
Cn
C 5n−1
5
Cn
…
…
…
…
…
…
…
…
…
…
k-1
k
C k−1
n−1
k
Cn
C kn−1
k
Cn
…
…
…
…
…
…
…
…
…
…
n-1
n
C n−1
n−1
n−1
Cn
Cn
n
(2.4.10) ережеге сәйкес кестенің кез келген C kn элементі жоғарғы жолда
тікелей осы элементтің үстіндегі элемент пен оның сол жағындағы
элементтің, яғни C kn−1 және C k−1
n−1 элементтерінің қосындысына тең.
3
2
3
Мысал, C 5=C 4 +C 4немесе 10=4+ 6.
n=0 , … ,10 үшін арифметикалық үшбұрыштың әртүрлілігі пирамида
түрінде 4-кестеде көрсетілген.
4-кесте
Арифметикалық үшбұрыш
∑
n
0
1
2
3
4
5
6
7
8
9
10
1
1
1
1
1
1
1
1
1
1
1
9
10
5
7
8
3
4
6
28
1
3
6
10
15
21
1
2
10
20
35
1
4
1
5
15
35
1
6
21
1
7
1
56
70
56
28
8
1
12 12
36 84
84
36
9
1
6 6
12 21
21 12
45
252
45 10 1
0 0
0 0
1
2
4
8
16
32
64
128
256
512
1024
Арифметикалық үшбұрышты қарастырудан шығады.
1. Үшбұрыштың төбесінде бір тұрады;
2. Үшбұрыштың бүйір қырлары бірлерден тұрады;
3. Үшбұрыштың жолдарының екінші және соңғысының алдындағы
цифрлары n санына тең;
4. Бір санын сыртында қамтитын кез келген цифр осы цифрдан жоғарыдағы сол жақтағы және оң жақтағы цифрлардың қосындысына тең
(Паскаль ережесі);
5. Үшбұрыштың әрбір жолындағы оның басынан және соңынан бірдей
қашықтықта жатқан цифрлар өзара тең (симметрия).
5-қасиет (арифметикалық үшбұрыш үшін). n-жолдағы элементтердің қосындысы 2n-ге тең
37.
n∑ C kn=2n .(2.4 .11)
k=0
Дәлелдеуі 4-кестені қарастырудан шығады.
6-ұасиет (арифметикалық үшбұрыш үшін). Арифметикалық
үшбұрышта n-жолының элементтерінің қосындысы (n-1)-жолдың элементтерінің қосындысынан екі есе үлкен.
Дәлелдеуі: Нақтысында (2.4.10) Паскаль ережесіне сәйкес (n-1)-ші
жолдың әрбір элементі, осы элементтің астында және оң жағында болатын
n-жолдың екі элементін құруға қатысады.
Сондықтан егер n-жолдың элементтерін біреуі арқылы қоссақ, онда осы
алынған қосындыға (n-1)-ші жолдың барлық элементтері бір бірден кіреді:
0
2
4
1
3
5
n−1
k
C n+ Cn +C n +…=C n+C n +C n+ …=∑ Cn−1 .(2.4 .12)
k=0
Бұдан басқа, 6-қасиет 3-, 4-кестелерін қарастырудан қарапайым
шығады.
Қайталанатын терулер
Қалауынша реттелмеген таңдама
xi , xi , … , xi ; ⏟
x j, x j , … , x j; … , ⏟
xν , xν , … , x ν
⏟
B=
(2.4 .13)
ξ
[
k1
k2
km
]
i, j, ν = 1,…m; ξ =1,…,N
бір және сондай
X ={ x 1 , x 2 , … , x m } (2.4 .14)
жиынының x 1 , x 2 , … , x mэлементтерінен құрылған, оның құрамына бірінші
типті k1 элементтері, екінші типті k2 элементтеріі, ... , m-типті km элементтері
кіретін және
k 1 + k 2+ …+k m =n(2.4 .15)
болатын n элементтерден m типтері бойынша қайталанатын терулер деп
аталады.
Қайталанатын терулердің санын C mn (n>m) деп белгілейміз. C mn
формуласын қорытып шығару үшін төрт типті самсалардан (бәліштер) он
самсаны таңдаумен түсіндіреміз, мысалы, эклерлерді (тәтті самсалар), буға
пісірілген самсаларды, қаттама самсаларды, жемісті самсаларды(n=10, m=4 ).
Төрт түрлі самсаларда он самсаны таңдаудың мүмкін бір нұсқасын
бірлерді және нөлдерді теру [11] арқылы көрсетейік:
⏟ 0 11
⏟ 0 11
⏟ } ,(2.4 .16)
{11⏟ 0 1111
k1
k2
k3
k4
мұнда, бірінші түрден екі самса, екінші түрден төрт самса, үшінші түрден екі
самса, төртінші түрден екі самса таңдалады. Нөлдер бірлердің төрт тобын
бөледі. Таңдаудың әр түрлі нұсқаларына он бірлерден және үш нөлдерден (n
38.
бірлер және m – 1 нөлдер) (2.3.18) түріндегі қайталанатын алмастыруларсәйкестенеді:
4
C 10=P ( 10,3 )=
13 !
=286.
3 ! 10 !
Жалпы жағдайда қайталанатын реттелмеген таңдаманы қайталанатын
алмастырулар сияқты мына түрде жазуға болады
Pξ =[ k 1 , k 2 , … , k m ] , ξ=1 ,… , N ,(2.4 .17)
мұндағы, ki (i = 1, ... , m) – бүтін оң сандар, X (2.4.14) жиынының
элементтерінің сандарына тең, олардың қосындысы (2.4.15)
n-ге тең
болатындай таңдалған. Әрбір ki-ді ki бірлер тобымен алмастырып, ал
олардың арасын нөлдермен толтырып, (n+ k – 1) элементтерден таңдаманы
аламыз. C mn таңдамалардың саны n бірлерден және (m – 1) нөлдерден тұратын
(2.3.18) түріндегі қайталанатын алмастырулардың санына тең:
m
C n =P ( n , m−1 )=
( n+m−1 ) !
.(2.4 .18)
( m−1 ) !n !
Бұдан басқа (2.4.18) формуласы (n+ m – 1) элементтерден m элемент-тер
бойынша (2.4.6) түріндегі қайталанбайтын терулер санын өрнектейді:
C mn =
( n+m−1 ) !
=C mn+ m−1 .(2.4 .19)
( m−1 ) !n !
2.5. Ньютон Биномы
Биномиалдық теорема
(a+ x) биномының оң бүтін дәрежесі үшін мына өрнектер алгебра
бастамасынан белгілі:
1
(a+ x ) =a+ x ,
2
2
2
(2.5 .1)
( a+ x) =a +2 ax+ x ,
3
3
2
2
3
( a+ x) =a +3 a x+3 a x + x .
{
Бұл теңдіктер x дәрежесі бойынша (a+ x)nжіктелуінің жалпы
формуласының дербес жағдайлары болатыны белгілі. (a+ x)n өрнегін n
биномдардың көбейтіндісі түрінде жазамыз:
( a+ x )n =⏟
( a+ x ) ( a+ x ) … ( a+ x ) . (2.5.2)
n рет
(2.5.2) теңдігінің оң жағын түрлендірмес бұрын қарапайым (2.5.1)
өрнектерін талдаймыз:
( a+ x )2= ( a+ x ) ( a+ x )=aa+ ax+ xa+ xx ; (2.5 .3)
( a+ x )3 =(a+ x)(a+ x)(a+ x)=¿
¿ aaa+ aax+ axa+ xaa+ axx+ xax + xxa+ xxx .(2.5 .4)
39.
(2.5.3) формуласына екі элементтерден (« x » және « a ») екі элементбойынша құрылған барлық қайталанатын орналастырулар кіреді, ал (2.5.4)
формуласына сондай екі элементтерден үш элемент бойынша барлық
қайталанатын орналастырулар кіреді. Осы сияқты ойлап, (2.5.2) үшін жалпы
жағдайда (a+ x) түріндегі n биномдарды қайта көбейткенде әрқайсысы n
элементтерден құрылған барлық мүмкін « x » және « a » әріптерінен
қайталанатын орналастыруларды
алатындығын тағайындауға болады.
Жалпы жағдайда құрамында k , x әріптер және (n – k ), a әріптер болатын
мүшелер ұқсас мүшелер болатындығына оңай (қарапайым) көз жеткіземіз,
яғни « x k » және « an−k », k =0 , ... ,n. Бұл мүшелер k әріптерден « x » және (n−k )
әріптерден « a » бойынша құрылған қайталанатын алмастыруларды көрсетеді,
ал сондай алмастырулардың саны (2.3.18)-ге тең:
P ( k , n−k )=
n!
k
=C n . ( 2.5 .5 )
k ! ( n−k ) !
Демек, ұқсас мүшелерді келтіргеннен кейін x k an−k өрнегі( a+ x )n жіктелуі
түріндегі C kn коэффициентімен кіреді.
Соңында мынаны аламыз:
n
n
( a+ x ) =∑ C kn x k an−k .(2.5 .6)
k=0
Нәтижесі (2.5.6) түріндегі Ньютон биномының формуласы деп
аталатын биномиалдық теорема дәлелденді. Мұндағы, C knсандары
биномиалдық коэффициенттер деп аталады. Басқаша (2.5.6) формуласы «х»
тәуелсіз айнымалысының дәрежесі бойынша Ньютон биномының жіктелуін
береді.
Қорытындыда (2.5.6) формуласын жалпы түрде алдын ала жазып,
алгебра бастамасында кездеспеген n=4 және n=5 үшін Ньютон биномы-ның
жіктелуінің формулаларын аламыз:
n
n
n (n−1) 2 n−2
k k n −k
n
x a +…+C n x a + …+ x ,(2.5.7)
2
(a+ x)4 =a 4+ 4 a3 x +6 a 2 x 2+ 4 a x 3 + x 4 ,(2.5 .8)
(a+ x)5=a5+ 5 a4 x +10 a3 x 2 +10 a2 x 3+5 a x 4 + x 5 .(2.5 .9)
(a+ x) =a +nx a
n−1
+
Биномиалдық коэффициенттердің қасиеттері
Егер дәрежелік қатар
2
k
a 0+ a1 x + a2 x +…+a k x +… (2.5.10)
қандай да бір аумақта φ (x) функциясына жинақталса, онда осы функция
a 0 , a 1 , a2 , ..., a k ,.. . сандарының тізбегі үшін туындатқыш функция деп аталады.
(2.5.6) теңдігінде параметр a=1 деп аламыз:
( 1+ x ) n=C 0n+ C1n x+ C2n x 2+...+C kn x k + …+Cnn x n .( 2.5.11)
Бұл жағдайда бұдан бұрын биномиалдық коэффициенттер деп аталған
C , k =0 , ... ,n сандары үшін (1+ x)n биномы туындатқыш функция болады.
(2.5.11) биномиалдық коэффициенттерін арифметикалық үшбұрыш-тың nжолының элементтерімен салыстырып, олардың бірдей екендігін байқаймыз.
Демек, кез келген n оң бүтін сандар үшін арифметикалық үшбұрышты
k
n
40.
биномиалдық коэффициенттердің практикалық түріндегі кестесі ретіндепайдалануға болады.
Жоғарыда келтірілген қиынырақ дәлелдеулермен салыстырғанда,
(2.5.11) туындатқыш функцияның көмегімен биномиалдық коэффициенттердің қасиеттері жеңіл түрде дәлелденеді.
1-қасиет. x бойынша жіктелген Ньютон биномының ақырларынан
(соңғы және алдыңғы мүшелерінен) бірдей қашықтықтағы C kn биномиалдық
коэффициенттері бір-біріне тең. Бұл теңдік (2.4.9) теңдігінен шығады:
k
n−k
C n=C n . (2.5.12)
Мысалы, жіктелуде
( a+ x )6 =a6 +6 a5 x +15 a 4 x 2 +20 a3 x 3+15 a 2 x 4 +¿
5
+6 a x + x
6
бірінші және соңғы мүшелердің коэффициенттері, екінші және соңғының
алдындағы, үшінші және соңынан үшіншінің коэффициенттері тең.
2-қасиет. « x » дәрежесі бойынша Ньютон биномының жіктелуіндегі
биномиалдық коэффициенттердің қосындысы 2n дәрежесіне тең ((2.4.11)
қараңыз):
n
∑ C kn=2n .(2.5.13)
k=0
Дәлелдеу үшін (2.5.11)-де x=1-ден аламыз, сонда:
n
n
0
n
1
n
k
n
n
n
n
( 1+1 ) =2 =C +C +C + …+C =∑ C kn .
k=0
3- қасиет . Паскаль ережесі (2.4.10):
k
k−1
k
C n=C n−1+C n−1 (2.5 .14)
Дәлелдеу үшін (2.5.14) теңдігін басқаша жазайық
k
k−1
k
C n+1=C n +Cn .(2.5 .15)
(2.5.11) туындатқыш функцияның сол және оң жақтарын (1+ x) -ке
көбейтеміз, ал сол жағын x дәрежесі бойынша Ньютон биномының жіктелуі
түрінде өрнектейміз, мұнда n орнына (n+1)-ді аламыз:
n+1
n
k=0
k=0
(1+ x)n +1=∑ C kn+1 x k =∑ C kn x k ( 1+ x ).(2.5 .16)
Оң жақтағы көбейтіндіні:
C 0n+ ( C 0n+ C1n ) x + ( C 1n +C2n) x 2 +...+ ( C k−1
+Ckn ) x k +...+C nn x n+ 1( 2.5.17)
n
деп жазамыз.
(2.5.16) теңдігінің сол жағын және (2.5.17)-ні салыстырып, (2.5.15)
ізделінді қатынасты аламыз:
k
C kn+1=C k−1
n +C n .
41.
4-қасиет. Жұп k биномиалдық коэффициенттерінің C kn қосындысы тақk коэффициентерінің C kn қосындысына тең:
0
2
2m
1
3
2m +1
C n+ Cn +...+C n + ...=C n+C n +...+C n
+…(2.5 .18)
Екі қосынды да ақырлы және 2 m> n, 2 m+ 1> n болғанда үзіледі.
Дәлелдеу үшін (2.5.11) де x=−1 деп аламыз.
0
1
2
3
k k
n n
0=Cn −Cn +C n−C n +…+ (−1 ) C n+ …+ (−1 ) Cn ,
бұдан (2.5.1.8) шығады.
2.6. Ықтималдылық есептерді комбинаторлық әдістермен шешудің
мысалдары
Жоғарыда қарастырылған комбинаторика әдістері (2.2.1) «классикалық» формуласымен ықтималдылықтарды тікелей кеңінен қолданылады.
Есептің мазмұнынан тәуелді бізді қызықтыратын оқиғаға сәйкес жалпы
жағдайлардың саны және қолайлы жағдайлардың саны комбинаторика
әдістерімен анықталады. Төменде ықтималдылық есептерін комбинаторика
әдістерімен шешудің мысалдарын қарастырамыз.
2.6.1-мысал. Ойын сүйегі екі рет лақтырылады. Бірінші және екінші лақтырылғанда ұпайлардың санының бірдей болуының ықтималдылығы қандай (А оқиғасы)?
Шешуі. Жағдайлардың жалпы саны N алты цифрдан { 1,2 , … ,6 } екі бойынша
алынған (2.3.9) түріндегі қайталаулар мен орналастырулардың санына тең:
2
2
N= A 6=6 =36.
А оқиғасына қолайлы жағдайлардың саны М А =6 , өйткені ойын сүйегін екі рет
лақтырғанда ұпайлардың теңесуінің саны алтыға тең: (1,1), (2,2), (3,3), ..., (6,6).
Соңында мынаны аламыз:
P( A)=
6 1
= =0,17.
36 6
2.6.2-мысал. Патрондар үшін револьвердің барабанында 7 ұя бар, оның бесеуіне
патрондар салынған (екеуі бос). Барабан айналымға келтіріледі және тоқтағаннан соң
шаппасын басады. Осы процедураны екі рет қайталағаннан кейін екеуінде де
атылмауының ықтималдығы қандай (от алмауы ескерілмейді)?
Шешуі. Жалпы жағдайлардың саны N 7-ден 2 бойынша алынған (2.3.9) түріндегі
қайталанатын орналастырулардың санына тең:
2
2
N= A 7=7 =49.
Ізделінді оқиғаға (оны B деп, белгілейміз) қолайлы жағдайлардың N саны
барабандағы 2 бос ұялардан 2 бойынша комбинациялардың (қайталанатын орналастырулардың) санына тең:
2
2
M B =A 2=2 =4.
Соңында мынаны аламыз:
P ( B )=
4
=0,08.
49
2.6.3-мысал. Урнада сипауға бірдей n қайта нөмірленген шарлар бар. Урнадан m
рет (m ≤n) қалауынша бір шардан алады және нөмірін жазып алғаннан кейін қайтадан
42.
урнаға салады. Осылай жазылған барлық нөмірлердің әртүрлі болуларының ( A оқиғасы)ықтималдығы қандай?
Шешуі. Жалпы жағдайлардың N саны n -нен m нөмірлері байынша алынған
қайталанатын орналастырулардың санына тең:
m
m
N= A n =n .
A оқиғасына қолайлы жағдайлардың саны қайталанбайтын орналастырулардың
санына тең (барлық жазылған нөмірлер әртүрлі болуы керек):
m
M A =A n =
Соңында мынаны аламыз:
n!
.
( n−m ) !
n!
P ( A )= m
.
n ( n−m ) !
2.6.4-мысал. Урнада сипауға бірдей 10 шарлар бар, олардың алтауы ақ және
төртеуі қара. Урнадан қалауынша 4 шарды алады. Алынған шарлардың арасында 2 ақ
және 2 қара шарлар болуының ( A оқиғасы) ықтималдығы қандай?
Шешуі. Жалпы алынған шарлардың N саны (2.4.5) түріндегі 10-нан 4 шар
бойынша қайталанбайтын терулердің (терулер) санына тең:
10 ·9 · 8 ·7
4
N=C 10=
=210.
1· 2 ·3 · 4
Ізделінді A оқиғасы қолайлы M A жағдайларының саны алты ақ шарлардан екі ақ
шарларды және сонымен бірге төрт қара шарлардан екі қара шарларды алудың әдістеріне
тең, яғни терулердің сандарының көбейтіндісі:
6 ·5 4 ·3
2 2
M A =C6 C 4=
·
=90.
1 ·2 1· 2
Соңында аламыз:
90 3
P ( A )=
= =0,43.
210 7
2.6.5-мысал. Алдыңғы мысалдың кеңейтілуі. N бұйымдардан құрылған партиядан
сапасын бақылау үшін қалауынша n бұйымдарды (n< N ) таңдайды. Партияда M ақаулы
бұйымдар бар. Таңдалған n бұйымдардың арасында m ақаулы ( A оқиғасы), m-нен көп
емес ақаулы ( B оқиғасы) бұйымдардың болуының ықтималдылығы қандай?
Шешуі. 2.6.4-мысалдағыдай ойлап, осыған ұқсас сандық есептерді шешу үшін
жалпы өрнекті аламыз:
m
n−m
m
C M C N− M
1
k
n− K
P ( A )=
,
P
(
B
)
=
C M C N− M .
∑
n
n
CN
C N k=0
2.6.6-мысал. Арасында 5 оқу озаттары бар 18 курсанттардан сынақ тапсыру үшін
әрқайсысы 9 адамнан құралған екі топты құрады. Келесі оқиғалардың ықтималдықтарын
тап: A барлық оқу озаттары бір топта болады. B екі оқу озаты бір топта, ал үшеуі басқа
топта болады.
Шешуі. Жалпы жағдайлардың N саны 18 курсанттардан 9 бойынша алынған
терулерге тең:
N=C 918.
A оқиғасына қолайлы жағдайлардың M A саны 5 оқу озаттарынан 5 бойынша
терулердің санын (барлық оқу озаттары бір топқа кіреді) 2 рет алынған 18-ге жетпейтін
қалған 13 курсанттардан 4 бойынша (топтың құрамы 9 адамға жетпегендіктен) терулердің
санына көбейткенге тең ( оқу озаттары бір немесе келесі топқа түсуі мүмкін):
43.
M A =2C 55 C 413.Нәтижесінде мынаны аламыз:
5
P ( A )=
4
2 C 5 C13
C
9
18
=
1
≈ 0,03.
34
M B жағдайларының саны тең:
2
7
3
6
M В =C5 ∙C 13+ C5 ∙C 13 ,
cоңында аламыз:
2
P ( A )=
7
3
6
C5 ∙ C13 +C5 ∙ C13
C
9
18
=
12
=0,7.
17
2.6.7-мысал. Он қабатты үйдің лифтісіне бірінші қабатта 3 адам кірді, әрқайсысы
бірдей ықтималдықпен кез келген қабатта (екіншіден- оныншы қабаттарда) шығады.
Келесі оқиғалардың ықтималдықтарын тап: A – барлығы бесінші қабатта шығады, B –
барлығы бір және сол қабатта шығады, C – адамдар әртүрлі қабаттарда шығады.
Шешуі. Берілген есепті «шариктерді» (лифтідегі жолаушыларды) «ойықтар»
(шұңқырлар,қабаттар) бойынша орналастыру есебіне келтіруге болады. Жалпы жағдайлар
N саны 9-дан 3 бойынша алынған қайталанатын орналастырулардың санына тең:
3
3
N= A 9=9 =729.
А, В, және С оқиғаларына қолайлы жағдайлардың саны сәйкесінше: MA = 1, MB =
9, МС үш жолаушыларды лифтіде 9 қабат бойынша таратудың әдістерінің санына
(біріншіден басқа), яғни қайталанбайтын орналастырулар санына тең:
3
M C = A 9=9 · 8· 7=504.
Соңында аламыз:
P ( A )=
1
=0,0014 ,
729
P ( B )=
9
=0,0123,
729
P (C)=
504
=0,69.
729
2.6.8-мысал. Шариктерді ойықтар бойынша таратудың жалпы есебі. m ойықтар
бойынша n шариктерді кездейсоқ лақтырады. n1+n2+ .. +nm=n болатындай бірінші
ойыққа n1 шариктер, екінші ойыққа n2 шариктер, ... , m-ге nm шариктер түсуінің (А
оқиғасы) ықтималдығын тап.
Шешуі. Жалпы жағдайлардың саны m-нен n бойынша қайталанатын орналастырулардың санына тең:
N= A nm=mn.
МА жағдайларының саны (2.3.8) түріндегі n шариктердің n1, n2,
қайталанатын алмастырулардың санына тең:
..., nm бойынша
44.
P ( n1 , n2 , … , nm ) =n!
n!
= m
.
n1 ! n2 ! … n m !
∏ ni !
i=1
Соңында аламыз:
n!
P ( A )=
.
m
n!
i
m ∏n
i=1
3-ТАРАУ
Ықтималдықтар теориясының негізгі теоремалары және формулалары
3.1.
Жиіліктерді және ықтималдықтарды көбейту теоремалары
Екі оқиғалардың көбейтіндісінің жиілігі сәйкесінше осы оқиғалардың
жиіліктерін көбейту теоремасымен анықталады.
¿
¿
Айталық A және B кездейсоқ оқиғалар, P ( A ) және P ( B ) – осы
¿
¿
оқиғалардың жиіліктері (1.2.1), P ( A∨B ) және P ( B∨ A ) – олардың шартты
жиіліктері (1.4.1, 1.4.3) болсын.
Жиіліктерді көбейту теоремасы. Екі оқиғалардың көбейтіндісінің
жиілігі біреуінің жиілігімен осы оқиға орындалғанда есептелген келесі
оқиғаның шартты жиілігінің көбейтіндісіне тең:
¿
¿
¿
P ( AB )=P ( A ) P ( B∨ A ) (3.1.1)
немесе
¿
¿
¿
P ( AB )=P ( B ) P ( A∨B ) .(3.1 .2)
Дәлелдеуі: Әрқайсысында A және B оқиғалары пайда болулары мүмкін
(оқиғалар үйлесімді) n тәуелсіз тәжірибелер жүргізілді деп ұйғарамыз.
Нәтижесінде m тәжірибелерде A оқиғасы, k тәжірибелерде B оқиғасы, l
тәжірибелерде A және B оқиғалары бірге орындалады.
A және B оқиғаларының жиіліктерін (1.2.1), олардың шартты
жиіліктерін (1.4.1) және көбейтіндінің жиілігін есептейміз:
m ¿
k ¿
l
, P ( B )= , P ( AB )= ,
n
n
n
(3.1.3)
m
m
l ¿
l
¿
AB
AB
P ( A∨B )=
= , P ( B∨A )=
= .
mB k
mA m
¿
P ( A )=
(3.1.3) өрнектерін (3.1.1) және (3.1.2) теңдіктеріне қойып, тепетеңдіктерді аламыз:
l m l l l k l l
= · = ; = · = .
n n m n n n n n
Екі оқиғалардың жиіліктерінің көбейтіндісінің теоремасы дәлелденді.
Тәжірибелердің n сандарын шексіз үлкейткенде A және B оқиғаларының
жиіліктері және шартты жиіліктері, A және B оқиғаларының көбейтіндісінің
жиілігі ықтималдық бойынша (1.2.7) оқиғаларының сәйкесінше ықтималдықтарына және шартты ықтималдықтарына жинақталады. Сондықтан жоғарыда
45.
дәлелденген оқиғалардың жиіліктерін көбейту теоремасы олардың ықтималдықтары үшін дұрыс болады.Екі оқиғалар үшін ықтималдықтарды көбейту теоремасы. Екі
оқиғалардың көбейтіндісінің ықтималдығы біреуінің ықтималдығын, осы
оқиға орындалғанда есептелген келесі оқиғаның шартты ықтималдығына
көбейткенге тең:
P ( AB ) =P ( A ) P ( B∨ A ) ,(3.1 .4)
P ( AB ) =P ( B ) P ( A∨B ) .(3.1.5)
Дәлелдеуі: Ықтималдықтарды көбейту теоремасын дәлелдеу жоғарыда
қарастырылған жиіліктерді көбейту теоремасы сияқты дәлелденеді, бірақ тек
қана жағдайлар сызбасы үшін мағынасы бар (үйлесімсіз, тең мүмкіндікті
оқиғалар, толық топты құрайтын оқиғалар). Жағдайлар сызбасында жатпайтын оқиғалар үшін ықтималдықтарды көбейту теоремасы аксиома түрінде
қабылданады және қарапайым оқиғалардың ықтималдықтарын көбейту
заңы деп аталады.
Оқиғалардың жиіліктерін көбейту теоремасын A1, A2, ... , An бірнеше
оқиғаларға кеңейтеміз (математикалық индукция әдісін жүйелі қолдану
жолымен)
¿
¿
¿
¿
¿
P ( A1 , A 2 , … , A n) =¿ P ( A1 ) P ( A2 ∨A 1 ) P ( A 3| A1 A 2 ) … P ( A n| A1 A 2 A 3 … An −1 ) .(3.1 .6)
Оқиғалардың нөмірленуінің реті – еркін.
Бірнеше оқиғалар үшін ықтималдықтарды көбейту заңы:
P ( A 1 , A 2 , … , A n ) =¿
¿ P ( A 1 ) P ( A 2∨ A1 ) P ( A 3|A 1 A 2 ) … P ( An| A 1 A2 A 3 … A n−1 ) (3.1 .7)
түрінде жазылады.
3.1.1-мысал. Урнада бірдей бес шарлар бар. Олардың екеуі ақ және үшеуі қара.
Урнадан қалауынша бір шарды алады, содан соң екіншісін алады. Шардың екеуі де қара
болуының ықтималдығы қандай?
Шешуі. A оқиғасы – екі қара шарлардың пайда болуы, A1 – бірінші рет алғанда
қара шардың пайда болуы, A2 – eкінші рет алғанда қара шардың пайда болуы. Сонда A
оқиғасы үшін өрнекті A1 және A2 оқиғаларының көбейтіндісі түрінде жазамыз:
A=A 1 A 2 .
А1 және А2 оқиғалары тәуелді, сондықтан (3.1.4) көбейту теоремасы бойынша
аламыз:
3 2 3
P ( A )=P ( A1 ) P ( A 2| A1 )= · = =0,30.
5 4 10
А2 оқиғасы А1-ден тәуелді, өйткені А1-дің пайда болуы тәжірибенің шартын
өзгертеді және бұдан А2 оқиғасының ықтималдығы өзгереді.
Егер А және В оқиғалары тәуелсіз ((1.5.3.), (1.5.4.)) болса, онда (3.1.1.),
(3.1.2) жиіліктерді көбейту теоремасы келесі түрді қабылдайды:
P¿ ( AB )=P¿ ( A ) P¿ ( B ) .(3.1.8)
Екі тәуелсіз оқиғалар үшін ықтималдықтарды көбейту заңы:
P ( AB ) =P ( A ) P ( B ) (3.1.9)
46.
болып жазылады.3.1.2-мысал. Бірінші мысалдың шартын қарастырамыз, бірақ тәжірибенің алғашқы
шарттарын қалпына келтіріп, бірінші шарды алғаннан соң оны кейін қайтарады.
Құрамында екі ақ шарлар және үш қара шарлар бар урнадан бірінші және екінші
алынғанда қара шарлар болу оқиғалары А1 және А2 тәуелсіз оқиғалар болып қала береді.
Шешуі. (3.1.9) формуласын қолданамыз:
3
∗3
5
9
.
P ( A )=P ( A1 A 2 )=P ( A 1) P ( A2 ) =
= =0,36
5
25
A
,
A
,…
,
A
Егер 1 2
3 оқиғалары тәуелсіз болса, ((1.5.6), (1.5.8) шарттары),
n
онда оқиғалардың көбейтіндісінің жиіліктері және ықтималдықтары үшін
(3.1.6) және (3.1.7) өрнектері:
n
P
¿
n
( )
(∏ ) ∏ ( )
∏ A i =∏ P¿ ( Ai ) ,(3.1.10)
i=1
i=1
n
n
P
i=1
Ai =
i=1
P A i (3.1.11)
түрінде жазылады.
Демек, n тәуелсіз оқиғалар жиілігі (ықтималдығы) осы оқиғалардың
жиіліктерінің (ықтималдықтарының) көбейтіндісіне тең.
3.1.3-мысал. Дайындық деңгейлері әртүрлі үш атқыш бір-бірінен тәуелсіз нысанаға
бір реттен оқ атады. Атқыштардың оқты нысанаға тигізуінің ықтималдықтары сәйкесінше
p1=0,90 , p2=0,60 , p3=0,50. Бір-бірден оқ атып, үш атқыштың да нысанаға дәл тигізу
ықтималдығы қандай?
Шешуі. Оқиғаларды былай белгілейміз: B – үш атқыш нысанаға тигізеді, B1–
бірінші атқыш нысанаға тигізеді, B2 – екінші атқыш нысанаға тигізеді, B3 – үшінші атқыш
нысанаға тигізеді. Сонда B оқиғасы B1 , B2 , B3 оқиғалары арқылы көбейтінді түрінде
өрнектеледі.
B=B1 B2 B 3 .
(3.1.11) теңдігіне сәйкес ( B1 , B2 , B3 оқиғалары тәуелсіз) P(B) тең:
P( B)=P( B1 )P( B2 ) P(B3 )= p1 p2 p3=0,90 • 0,60• 0,50=0,27.
3.2. Жиіліктерді және ықтималдықтарды қосу теоремалары
Екі оқиғалардың қосындысының жиілігі осы оқиғалардың жиіліктерін
қосу теоремасына сәйкес анықталады.
Жиіліктерді қосу теоремасы. Үйлесімсіз екі оқиғалардың қосындысының жиілігі осы оқиғалардың жиіліктерінің қосындысына тең:
¿
¿
¿
P ( A+ B )=P ( A ) + P ( B ) AB=∅ болса .(3.2 .1)
Дәлелдеуі: Әрқайсысында А оқиғасы немесе В оқиғасы пайда болатын
n тәуелсіз тәжірибелер жүргізіледі деп ұйғарамыз. Нәтижесінде A оқиғасы m
тәжірибелерде, ал B оқиғасы k тәжірибелерде пайда болады. А және В
оқиғаларының жиіліктері сәйкесінше тең ((1.2.1) қараңыз):
47.
¿P ( A)=
m ¿
k
, P ( B )= .(3.2 .2)
n
n
A және B оқиғалары үйлесімсіз болғандықтан, олар бірге пайда
болатын тәжірибелер жоқ. Олардың қосындысы C= A+B оқиғасы (1.1.4) (m+k )
тәжірибелерде ((1.1.5) қараңыз, 1.1.11-сурет) A оқиғасының немесе B
оқиғасының пайда болуынан тұрады.
Демек,
¿
P ( A+ B )=
m+k
.(3.2 .3)
n
(3.2.2), (3.2.3) өрнектерін (3.2.1) формуласына қойып, мына тепетеңдікті аламыз:
m+ k m k
= + .
n
n n
Екі оқиғалардың жиіліктерін қосу теоремасы дәлелденді. n тәжірибелер
санын шексіз үлкейткенде оқиғаның жиілігі ықтималдық бойынша оқиғаның
ықтималдылығына (1.2.7) жинақталады.
Екі оқиғалардың ықтималдылықтарын қосу теоремасы. Үйлесімсіз
екі оқиғалардың қосындысының ықтималдылығы осы оқиғалардың, ықтималдықтарының қосындысына тең:
P ( A + B )=P ( A ) + P ( B ) AB≠ ∅ болса.
(3.2 .4)
Дәлелдеуі. Екі оқиғалар үшін ықтималдықтарды қосу теоремасы тек
қана жағдайлар сызбасында (үйлесімсіз, тең мүмкіндікті оқиғалар,толық
топты құрайтын оқиғалар) жиіліктерді қосу теоремасы сияқты дәлелденеді.
Жағдайлар сызбасында жатпайтын кездейсоқ оқиғалар үшін ықтималдықтарды қосу теоремасы аксиома түрінде қабылданады және оқиғалардың
ықтималдықтарын қосу заңы деп аталады.
Екі оқиғалар үшін жиіліктерді қосу теоремасына математикалық
индукция әдісін жүйелі қолданып, оны бірнеше A1 , A 2 ,… , An үйлесімсіз
оқиғаларына кеңейтуге болады
n
( )
n
P¿ ∑ A i =∑ P¿ ( A i) ,( 3.2.5)
i=1
n
( )
i=1
n
P ∑ A i =∑ P ( A i ) .(3.2.6)
i=1
i=1
3.2.1-мысал. Центрлері бір нүктеде, бір-біріне іштей сызылған үш дөңгелектен
тұратын нысанаға бір рет оқ атылады. Орталық дөңгелекке және сақиналарға оқтың
тиюінің ықтималдықтары сәйкесінше Р1=0,10, Р2=0,20, Р3=0,30. Бір рет оқ атқанда
нысанаға тиюдің ықтималдығы қандай?
3.2.1-сурет. Нысананың сызбасы
48.
Шешуі. Оқиғаларды белгілейміз. А – бір атқанда оқтың нысанаға тиюі, Аі –нысананың і-ші бөлігін (і=1, 2, 3) тигізу. Сонда А оқиғасын үйлесімсіз А1, А2, А3 (шекараға
тигізу жақсы нәтиже) қосындысы түрінде жазуға болады:
A=A 1 + A 2 + A 3 .
А оқиғасының ықтималдығы (3.2.6) формуласына сәйкес А1, А2, А3 оқиғаларының
ықтималдықтарының қосындысына тең:
P ( A )=P ( A1 ) + P ( A2 ) + P ( A3 ) = p1 + p 2+ p 3 ,
P ( A )=0,10+ 0,20+0,30=0,60.
3.2.2-мысал. Лотереяда 100 билет бар. Олардың 1 билетіне 1000 теңге, 5 билетіне
200 теңге, 10 билетіне 50 теңгелік ұтыстар түседі. Қалған билеттерге ұтыстар түспейді.
Сатып алынған бір билетке ең болмағанда 50 теңге ұтудың (А оқиғасы), 50 теңгеден көп
ұтудың (В оқиғасы) ықтималдықтары қандай?
Шешуі. Лотерея ойынының нәтижелерін белгілейміз:
А1- 50 теңгені ұту;
А2 - 200 теңгені ұту;
А3 - 1000 теңгені ұту;
Сонда:
A=A 1 + A 2 + A 3 , B=A 2 + A 3 .
Оқиғалардың ықтималдықтарына тең:
10
5
1
P ( A 1 )=
=0,10 , P ( A 2 )=
=0,05 , P ( A 3 )=
=0,01.
100
100
100
А1, А2, А3 оқиғалары үйлесімсіз (бір тиражда бір билетке екі ұтыс шығуы мүмкін емес)
екендігін ескеріп, (3.2.6) ықтималдықтарды қосу теоремасы бойынша аламыз,
P ( A )=P ( A1 + A2 + A3 ) =P ( A 1 ) + P ( A 2 ) + P ( A3 ),
P ( A )=0,10+ 0,05+0,01=0,16;
P ( B )=P ( A 2 + A 3 )=P ( A 2) + P ( A 3 ),
P ( B )=0,05+0,01=0,06.
Қосу теоремасының тек қана үйлесімсіз оқиғалар үшін дұрыс
екендігін жоғарыда айттық. Оқиғалар үйлесімді (1.1.12-суретті қараңыз)
болған жағдайда оқиғалардың қосындысының орнына олардың бірігуін
қарастырамыз деп біз келіскенбіз (1.1.6), мысалы,
K=C ∪ D .(3.2 .7)
Сонда К оқиғасының ықтималдығы:
P ( K )=P ( C )+ P ( D )−P ( CD ) (3.2 .8)
өрнегімен анықталады.
3.2.3-мысал. (1.1.7 мысалының шешуі). Екі монетаны лақтыру жүргізіледі. Мына
оқиғалар қарастырылады:
С – ең болмағанда бір гербтің пайда болуы;
Д – ең болмағанда бір цифрдың пайда болуы;
СД – бір гербтің және бір цифрдың пайда болуы (1.1.13-сурет):
K=C ∪ D .
К оқиғасының – тәжірибенің кез келген нәтижесінің пайда болу ықтималдығын
тап.
Шешуі. С, Д және СД оқиғаларының ықтималдықтары тең:
3
3
2
P ( C ) = , P ( D )= , P ( CD )= .
4
4
4
С және Д оқиғаларының бірігуінің ықтималдығы тең:
3 3 2
P ( K )=P ( C ∪ D )=P ( C ) + P ( D )−P ( CD )= + − =1.
4 4 4
49.
Бұдан шығады, К оқиғасы ақиқат,K¿ Ω .3.3.
Қосу теоремасының салдарлары
Үйлесімсіз оқиғалардың қосындысымен байланысқан толық топты
құрайтын, басқаша айтқанда, оқиғалардың толық кеңістігімен ықтималдылық
есептерін тәжірибеде шешу үшін ықтималдықтарды қосу теоремасының
(заңының) екі маңызды салдарлары бар.
1-салдар. Толық топты құрайтын A1, A2, ... , An үйлесімсіз
оқиғаларының ықтималдықтарының қосындысы бірге тең:
n
∑ P ( Ai ) =1 ; A i A j=∅ , i, j=1, … , n ; i≠ j .(3.3 .1)
i=1
Дәлелдеуі. Tолық топты құрайтын A1, A2, ... , An (оқиғалардың толық
кеңістігі) оқиғаларының қосындысы – ақиқат оқиға, өйткені тәжірибенің
нәтижесінде олардың ең болмағанда біреуінің пайда болуы міндетті, яғни
n
∑ A i=¿ Ω , ¿
i=1
ал ақиқат оқиғаның ықтималдығы, демек, қосындының ықтималдығы бірге
тең:
n
( )
P ∑ A i =∑ P(Ω)=1.
i=1
Басқа жағынан, (3.2.6) түріндегі ықтималдықтарды қосу заңына сәйкес,
үйлесімсіз оқиғалар қосындысының ықтималдығы осы оқиғалар ықтималдықтарының қосындысына тең:
n
( )
n
P ∑ A i =∑ P ( A i )=1.
i=1
i=1
2-салдар. Қарама-қарсы оқиғалар ықтималдықтарының қосындысы
бірге тең:
P ( A ) + P ( A )=1 .(3.3 .2)
Дәлелдеуі. Cалдар жоғарыда дәлелденген 1-салдардың n=2 болғандағы
дербес жағдайы (екі оқиғалар үшін). Толық топты құрайтын екі үйлесімсіз
оқиғалар қарама-қарсы оқиғалар деп аталады. Қарама-қарсы оқиғалар үшін
(1.1.12) және (1.1.13) қатынастары дұрыс:
A+ A=Ω, .(3.3 .3)
A∗A=∅ .
}
Олардың қосындысының ықтималдығы бірге тең:
P ( A + A ) =P ( Ω )=1 ,(3.3 .4)
ал қосу теоремасы бойынша
P ( A + A ) =P ( A )+ P ( A ) .(3.3 .5)
(3.3.4) және (3.3.5) теңдіктерін біріктіріп, (3.3.2) теңдігін аламыз, яғни
2- салдар дәлелденді.
Ықтималдылық есептерді шығарғанда бұл салдар жиі:
P ( A )=1−P ( A ) (3.3.6)
50.
түрінде қолданылады.Практикада бұл мынаны көрсетеді, А оқиғасының ықтималдығын
қарама-қарсы A оқиғасының ықтималдығы арқылы есептеуге болады, көп
жағдайда A оқиғасының ықтималдығы А оқиғасының ықтималдығына қарағанда жеңіл анықталады.
Жоғарыда қарастырылған 3.2.1- және 3.2.2-мысалдарын шешу үшін
қосу теоремасының 2-салдарын қолданайық.
3.3.1-мысал. (3.2.2-мысалының шешуі). Бір рет оқ атқанда (А оқиғасы) нысанаға
тигізудің ықтималдығын қарама-қарсы A оқиғасының – бір рет оқ атқанда тимеуі арқылы
шешеміз:
P ( A )=0,40 , P ( A )=1−P ( A )=1−0,40=0,60.
3.3.2-мысал. (3.2.2-мысалды шешу). Ең болмағанда 50 теңге ұту есебін шешу (А
оқиғасы) үшін A қарама-қарсы оқиғасын – лотереяда ұтыс жоқ оқиғасын қолданамыз:
100−16 84
P ( A )=
=
=0,84 ,
100
100
P ( A )=1−P ( A )=1−0,84=0,16.
3.3.3-мысал. Үш монетаны лақтыру жүргізіледі. Гербтің ең болмағанда бір рет
түсуінің ықтималдығы қандай?
Шешуі. Осы тәжірибе нәтижелерінің (оқиғаларының) кеңістігін үш монетада
гербтердің түсуі тұрғысынан қарастырамыз. Гербтердің түсуінің саны 0, 1, 2, немесе 3
екендігі қарапайым түсінікті. Оқиғаның ізделінді ықтималдығы - монеталарды үш рет
лақтырғанда ең болмағанда, бір рет герб түсуінің (А оқиғасы) ықтималдығы төрт мүмкін
нәтижелердің үшеуінің А1, А2, А3 ықтималдықтарының қосындысына тең ( Ak −¿k
гербтердің пайда болуы, k=1,2,3):
P ( A )=P ( A1 ) + P ( A2 ) + P ( A3 ) .
А оқиғасына қарама-қарсы оқиға А0 үш монетаны лақтырғанда бірде-бір рет герб
түскен жоқ. Оның ықтималдығы тең:
3
3
P ( A 0 ) =q =0,50 =0,125 ,
мұнда, q=1− p=1−0,50 , p=0,50 – бір рет монетаны лақтырғанда гербтың пайда болу
ықтималдығы.
Сонымен, ақырында, ізделінді Р(А) ықтималдығы
3
P ( A )=1−P ( A )=1−P ( A0 ) =1−(1− p) ,
P ( A )=1−0,125=0,875.
Мысалдарды қарама-қарсы оқиғалар арқылы шешу тиімді екендігі қарапайым.
3.4. Бірнеше тәуелсіз тәжірибелерде оқиғалардың ең болмағанда бір
рет пайда болуының ықтималдығы
3.3.3-мысалында алынған нәтиженің кеңейтілуін бірдей немесе өзгермелі шарттарда орындалатын n тәуелсіз тәжірибелердің жағдайында қарастырамыз.
Шарттары тәжірибеден тәжірибеге өзгеріп отыратын n тәуелсіз
тәжірибелер жүргізілсін. Мысалы, спорттық пистолеттен нысанаға атыс
шығаратын атқыш, әрбір атыстан кейін нысанаға бағыт бойынша бір қадам
жасайды. Нысанаға тигізудің ықтималдығы әрбір атыс сайын өсетіндегі
түсінікті.
51.
Белгілейміз Ai – і-ші атқанда нысанаға тигізу, і =1, 2, ... , n, Аi – і-шіатқанда тимеу, В – n рет атқанда ең болмағанда, бір рет тигізу, P( B)=R1 , n – n
рет атқанда ең болмағанда, бір рет тигізудің ықтималдығы, B – n рет атқанда
нысанаға бірде-бір рет тигізбеу. Сонда В оқиғасы мына түрде өрнектелуі
мүмкін:
B= A 1 A2 … A n + A1 A 2 A 3 … An + …+ A 1 A 2 … A n−1 A n + A1 A 2 A 3 … A n++ A 1 A 2 A3 A 4 … An + A1 A2 … A
B қарама-қарсы оқиғасы мына түрде өрнектелуі мүмкін:
B= A 1 A2 … A n ,(3.4 .2)
ал оның ықтималдығы тең:
n
( )
n
P ( B )=P ∏ A i =∏ P ( A i ) .(3.4 .3)
i=1
i=1
і-ші тәжірибеде і-ші рет атқанда нысанаға тигізудің Аі оқиғасының
ықтималдығын Рі=Р(Аі) арқылы, ал тигізбеудің ықтималдығын – Аi оқиғасы
пайда болуының ықтималдығын
P ( A i )=qi=1− pi=1−P ( A i) , i=1 , … , n
арқылы белгілейміз. Сонда (3.4.3) өрнегін:
n
n
P ( B )=∏ qi=∏ ( 1−p i ) (3.4 .4)
i=1
i=1
деп жазуға болады.
(3.3.6)-дан шығады
R1 , n=P ( B ) =1−P ( B ) , (3.4 .5)
бұдан:
n
n
R1 , n=1−∏ qi =1−∏ ( 1− pi ) .(3.4 .6)
i =1
i=1
Тәжірибедегі шарттар өзгермесе (мысалы, нысанаға атыс тек қана бір
позицияда жүргізілсе)
P ( A i )=P ( A )= p ,
(3.4 .7)
P ( A i ) =P ( A )=q=1− p .
Алынған нәтижелер (3.4.6)-ға қойсақ, соңында аламыз:
n
n
R1 , n=1−q =1−( 1− p ) .(3.4 .8)
(3.4.6) формуласы шарттары тәжірибеден тәжірибеге өзгеретін n
тәуелсіз тәжірибелер жүргізгенде оқиғаның ең болмағанда, бір рет пайда
болуының ықтималдығын R1 , n есептеуде қолданылады. (3.4.8) формуласы
шарттар өзгермегенде (тұрақты) n тәуелсіз тәжірибелер жүргізгенде
оқиғаның ең болмағанда, бір рет пайда болуының ықтималдығын R1,n
есептеуге мүмкіндік береді.
3.4.1-мысал. Қандай да бір бұйымды дайындауда үш жұмысшы бір-бірінен тәуелсіз
жүйелі жұмыс жасайды, бұл жағдайда бұйымды келесі жұмысшыға бергенде бұйымның
сапасы тексерілмейді. Бірінші жұмысшының ақау жіберу ықтималдығы p1=0,10,
екіншісінің ақау жіберу ықтималдығы р2=0,08, үшіншісінің aқау жіберу ықтималдығы
р3=0,05. Бұйымды дайындауда бұйымның ақаулы болуының ықтималдығы қандай?
52.
Шешуі. Үш жұмысшының бұйымды дайындаудағы ақау жіберу оқиғасы А болсын.А оқиғасы орындалады, егер ең болмағанда, бір жұмысшы ақаулы бұйым шығарса. Сонда
(3.4.6) формуласымен аламыз:
P ( A )=R1,3 =1−( 1− p2 ) ( 1− p2 ) ( 1− p3 ) =1−0,90 · 0,92· 0,95=0,21.
3.4.2-мысал. Ғарыш обьектілерінің ізіне түсудің радиолокациялық станциясы (ІРС)
бір рет циклдік шолуда обьектіні р=0,80 ықтималдықпен сыртынан бақылайды. ІРС әрбір
циклдегі шолуының объектіні сырттан бақылауы басқа циклдерден тәуелсіз өтеді. ІРС
шолатын зонаның ішінде обьектіні табу уақытында ІРС 5 цикл жасап үлгереді. Обьектіні
табудың ықтималдығы қандай?
Шешуі. n циклдік шолуда (n=5) ІРС-ның объектіні сыртынан бақылауын В деп
белгілейік. Ең болмағанда, бір циклде объектіні сыртынан бақыласа, В оқиғасы пайда
болады . (3.4.8) формуласымен ізделінді ықтималдықты есептейміз
5
5
P ( B )=R1,5 =1−( 1− p ) =1−0,20 =0,99968.
3.4. Толық ықтималдықтар формуласы
Толық ықтималдықтар формуласы ықтималдықтарды қосу және
көбейту теоремаларының салдары болады. Осы формула әртүрлі жағдайда
әртүрлі ықтималдықпен өтетін оқиғаның ықтималдығын анықтауға
мүмкіндік береді, сонымен бірге осындай жағдайлардың ықтималдықтарын
тәжірибеге дейін бағалауға болады, ал қарастырылған оқиғалардың пайда
болуының шартты ықтималдықтары әрбір орындалатын жағдайларда белгілі
болуы тиіс. Жоғарыдағы айтылғандарды ескерсек, ізделінді ықтималдық
орташа салмақты ықтималдық түрінде анықталады, ал бұл жағдайда берілген
оқиға өтетін барлық мүмкін жағдайлардың ықтималдықтары салмақтар
болады.
Айталық тәжірибенің шарттарынан (жоғарыда айтылғандай, жағдайлардан) тәуелді кездейсоқ А оқиғасының Р(А) ықтималдығын анықтау керек.
Мұндай шарттар жөнінде өзін-өзі теріске шығаратын n ұйғарымдар
(гипотезалар) жасауға болады:
H1 , H2 , … , Hn¿
Әрбір H i (i=1,2 , … n) ұйғарымы (болжамы, гипотезасы) ықтималдығы
тәжірибеге дейін (априорлы*) қандай да бір ықтималдықпен
P ( H 1 ) , P ( H 2 ) , … , P ( H n ) (3.5.2)
бағаланатын кездейсоқ оқиғаны көрсетеді.
Априорлы ықтималдықтар деп аталатын ұйғарымдар (болжамдар)
ықтималдықтарының қосындысы бірге тең ((3.3.1) қосу теоремасының
салдары):
n
∑ P ( H i ) =1(3.5 .3)
i=1
толық топты құрайтын үйлесімсіз оқиғалардың (гипотезалардың)
ықтималдықтарының қосындысы секілді.
Бұдан басқа әрбір Ні ұйғарымында і=1,2,…,n А оқиғасының пайда
болуының шартты ықтималдықтары P ( A∨H i ) белгілі және мынаған тең:
P ( A∨H 1 ) , P ( A∨H 2 ) , … , P ( A∨H n ) ( 3.5.4)
53.
Ні, і=1,2,…, n оқиғаларымен (3.5.1-сурет) үйлесімсіз қиылысулардың(көбейтінділердің) қосындысын құрай отырып:
n
A=H 1 A+ H 2 A+…+ H n A=∑ H i A (3.5 .5)
i=1
жоғарыда айтылғандардың негізінде А оқиғасы тек қана ұйғарымдардың
бірімен бірге пайда бола алады.
А оқиғасының ізделінді Р(А) ықтималдығын сәйкесінше ықтималдықтарды қосу теоремасымен (3.2.6) анықтаймыз:
(
n
)
n
P ( A )=P ∑ H i A =∑ P ( H i A ) ,(3.5 .6)
i=1
i=1
ал ықтималдықтарды көбейту теоремасының (3.1.4) негізінде:
P ( H i A )=P ( H i ) P ( A∨H i ) , i=1 ,… ,n (3.5.7)
өрнегін аламыз.
(3.5.7)-ні (3.5. 6) формуласына қойсақ, соңында мынаны аламыз:
3
P ( A )=∑ P ( H i ) P ( A∨H i ) .(3.5 .8)
i=1
*A priori (латынша) – біріншіден, яғни бұл жағдайда «тәжірибеге дейін».
3.5.1-сурет. А оқиғасының және Ні оқиғаларының (гипотезаларының)
көбейтінділері
Осы формула – толық ықтималдықтар формуласы. (3.5.8) формуласы
А оқиғасының толық ықтималдығын априорлы ықтималдықтардыңболжамдардың Р(Ні ) ықтималдықтарын әрбір Ні болжамында А
оқиғасының Р(А|Ні) шартты ықтималдықтарына көбейтінділерінің
қосындысы секілді есептеуге мүмкіндік береді.
(3.5.8) формуласын мынадай жағдайларда: тәжірибеге дейін бағаланатын априорлық ықтималдықтармен (3.5.2) кездейсоқ нәтижемен тәжірибенің
шарттары жөнінде өзін-өзі теріске шығаратын ұйғарымдар (3.5.1) жасауға
болса, ал оқиғаның ықтималдығы тәжірибенің шартынан (3.5.4) тәуелді
өзгерсе қолданады.
3.5.1-мысал. Фин шығанағындағы берілген ауданда тікұшақ құтқарғыш балықшылармен мұздықты іздеуді жүргізеді, жылдың осы уақытында метеобайқаудың болжамы
бойынша барлық жағдайлардың 60 %-ы қарлы, бұлтты ауа райы болады, ал 40%-ы жай
бұлтты ауа райы болады. Жай бұлтты ауа райында балықшылармен мұздықты табу
54.
p1=0,90 ықтималдықпен, ал бұлтты ауа райында p2=0,60 ықтималдықпен бағаланады. Әртүрлі ауа райының шарттарында балықшыларды табудың ықтималдығы қандай?
Шешуі. Белгілейміз:
А – балықшылар мен мұздық тікұшақпен іздеу мезгілінде табылады;
Н1 – іздеу қолайлы ауа райында орындалады;
Н2 – іздеу қолайсыз ауа райында орындалады (күрделі метеошарттарда).
Априорлық ықтималдықтар (гипотезалардың ықтималдықтары) есептің шарты
бойынша мынаған тең: P ( H 1 )=0,40 , P ( H 2 )=0,60 , (3.5.3) формуласы бойынша
P ( H 1 ) + P ( H 2 )=0,40+ 0,60=1,00 .
Әрбір гипотезадағы А оқиғасының шартты ықтималдықтары:
P ( A∨H 1 ) = p1=0,90 , P ( A∨H 2 ) =p 2=0,60.
Ізделінді ықтималдық – толық ықтималдық Р(А) (3.5.8) формуласымен есептеледі:
P ( A )=P ( H 1 ) P ( A∨H 1 ) + P ( H 2 ) P ( A∨H 2 ),
P ( A )=0,40 · 0,90+0,60 · 0,60=0,72.
3.5.2-мысал. Үш зауытта дайындалған детальдар үш бірдей жәшікте сақталады.
Сенімділігі (t уақытында тоқтаусыз жұмыс жасау ықтималдығы) p1=0,90 болатын бірінші
зауытта дайындалған детальдар бірінші жәшікте, сенімділігі p2=0,05 екінші зауытта
дайындалған детальдар екінші жәшікте, сенімділігі p3=0,80 үшінші зауытта дайындалған
детальдар үшінші жәшікте сақталады. Ақаулы детальды алмастыру үшін үш жәшіктің
біреуінен қалауынша деталь таңдалады. Таңдалған детальдың белгілі t уақыт ішінде
сенімді жұмыс жасауының ықтималдығы қандай?
Шешуі. А – таңдалған деталь t уақытында тоқтаусыз жұмыс жасау оқиғасы. А
оқиғасына қарағанда үш ұйғарымды жасаймыз:
Н1 – деталь бірінші зауытта дайындалған (бірінші жәшіктен таңдалған);
Н2 – деталь екінші зауытта дайындалған (екінші жәшіктен таңдалған);
Н3 – деталь үшінші зауытта дайындалған (үшінші жәшіктен таңдалған).
Үш жәшік бірдей болғандықтан, априорлық ықтималдықтары мынаған тең:
1
P( H 1 ) =P ( H 2 ) =P ( H 3 )= =0,33 .
3
A оқиғасының шартты ықтималдықтары мынаған тең:
P ( A∨H 1 ) = p1=0,90 ;
P ( A∨H 2) = p2=0,95 ;
P ( A∨H 3 ) = p3=0,80.
(3.5.8) формуласы бойынша А оқиғасының толық ықтималдығы мынаған тең:
3
P ( A )=∑ P ( H i ) P ( A∨H i ) =0,33 · 0,90+ 0,33 ·0,95+ 0,33· 0,80=0,88.
i=1
3.6. Бейес формуласы (болжамдар теоремасы)
Бейес формуласы* (болжамдар теоремасы) (3.5.8) толық ықтималдықтар формуласының және ықтималдықтарды көбейту теоремасының салдары
болады. Осы формула тәжірибенің нәтижесін ескеріп, P(H i ) априорлық
ықтималдықтарды қайта есептеуге, апостериорлық** ықтималдықтар деп
аталатын P ( H k ∨ A )ықтималдықтарды анықтауға мүмкіндік береді. Айталық, А
оқиғасы пайда болатын тәжірибенің шарттары жөнінде өзін-өзі теріске
шығаратын болжамдар жасауға болады:
H 1 , H 2 , … , H n ; H i , H j=∅ , i, j =1 ,… , n ; i≠ j (3.6 .1)
55.
оқиғалардың толық тобын құрайтын, яғниn
∑ H i =Ω .(3.6 .2)
i=1
Болжамдардың ықтималдықтары (априорлы ықтималдықтар) тәжірибеге дейін бағаланады және белгілі:
n
P ( H 1 ) , P ( H 2 ) , … , P ( H n ) ; ∑ P(H i )=1.(3.6 .3)
i=1
Тәжірибенің нәтижесінде А оқиғасы орындалады деп ұйғарамыз. Осы
фактіні ескерумен (3.6.3) априорлы ықтималдықтарды қайта есептейміз,
шартты ықтималдықтар болатын апостериорлы** ықтималдықтарды анықтаймыз
* Ағылшын математигі Томас Бейес (T.Bayes) (1702-1761) атымен аталған.
Ықтималдықтар теориясы бойынша Т. Бейестің жұмыстары 1763 жылы “Ықтималдықтар
теориясы бойынша есептерді шешу тәжірибесі” атымен жарияланды.
** A posteriori (лат) – кейін, бұл жағдайда “тәжірибеден кейін”
P ( H 1| A ) , P ( H 2| A ) ,… , P ( H n| A ) . ( 3.6 .4 )
H k A , k=1 , … , nкөбейтіндісін
қарастырамыз
және
(3.1.4),
(3.1.5)
ықтималдықтарды көбейту тоеремасы бойынша оның ықтималдығын екі
формада жазамыз
P(H k ∨A )=P(H k )P( A∨H k )=P( A) P( H k ∨ A).(3.6 .5)
(3.6.5) теңдігінің оң жақтағы екеуін P(A)≠0-ге бөлеміз және теңдеуді P(
H k ∨ A ) қарағанда шешеміз:
P ( H k| A ) =
P ( H k ) P ( A|H k )
P(A)
, k=1 , … , n(3.6 .6)
Осы формула Бейес формуласы. Қажет болғанда P(A) ықтималдығы
(3.5.8) толық ықтималдықтар формуласы бойынша анықталады. Сонда (3.6.6)
формуласы:
P ( H k ) P ( A|H k )
P ( H k| A ) = n
, k=1 , … , n(3.6 .7)
∑ P ( H i ) P ( A|H i )
i =1
деп жазылады.
Иллюстрация үшін алдыңғы параграфтың мысалдарын қарастырамыз,
апостериорлы ықтималдықтарды Бейес формуласымен есептейміз.
3.6.1-мысал.
3.5.1-мысалының
шарттарында
P( H 1∨ A)және
P(H 2∨ A)
апостериорлы ықтималдықтарды анықтаймыз, яғни мұздықты іздеудің сәйкесінше
56.
қолайлы немесе қолайсыз ауа райында орындалғандығының ықтималдықтарын, егер Аоқиғасы – балықшылармен мұздықты табу пайда болды деп есептесек.
Шешуі. (3.6.6) Бейес формуласы бойынша мынаны аламыз:
P ( H 1 ) P ( A|H 1 ) 0,40 · 0,90
P(H 1∨ A)=
=
=0,50 ,
0,72
P( A)
P( H 2∨ A)=
P ( H 2 ) P ( A∨H 2 )
P ( A)
=
0,60 ·0,60
=0,50.
0,72
Тәжірибенің нәтижесінде А оқиғасы орындалды деген факт апостериорлы
ықтималдықтар P( H 1∨ A) және P( H 2∨ A) мәндеріне әсер етті, сондықтан P( H 1 )=0,40
және P( H 2 )=0,60 априорлы ықтималдықтар мәндеріне қарағанда бірдей және тең болып
қалды.
3.6.2-мысал. 3.5.2-мысалының шарттары бойынша А оқиғасы – қандай да бір
жәшіктен таңдалған детальдың t уақытында тоқтаусыз жұмыс жасауы орындалды деген
шартпен
P(H 1∨ A),
P( H 2∨ A)
және
P(H 3∨ A)
апостериорлы
ықтималдықтарын
анықтаймыз.
Шешуі. (3.6.6) Бейес формуласы бойынша:
P ( H 1 ) P ( A|H 1 ) 0,33 · 0,90
P( H 1∨ A)=
=
=0 , 34 ,
0,88
P( A)
P( H 2∨ A)=
P ( H 2 ) P ( A|H 2 )
P( A)
=
0,33· 0,95
=0,36 ,
0,88
P( H 3∨ A)=1−(P ( H 1∨ A)+ P( H 2∨ A))=1−(0,34+ 0,36)=0,30.
Екінші жәшіктегі детальдардың өте үлкен сенімділігі (0,95) апостериорлы
ықтималдық шамасының P(H 2∨ A)=0,36априорлық мәнге P( H 2 )=0,33 қарағанда өсу
жағына әсер еткенін көреміз. Үшінші жәшіктегі детальдардың өте төмен сенімділігі (0,80)
басқаларына
қарағанда
апостериорлы
ықтималдықтың
P( H 3∨ A)=0,30
априорлы
P( H 3 )=0,33 ықтималдықпен салыстыру бойынша азаюына әсер етті.
Бейес формуласы бойынша робототехникада қолданылатын образдарды тану жүйесін және өзін-өзі оқыту жүйесін құрғанда кең қолданыс табады.
Осындай жүйелер роботтың алдағы бағытында шешімдер қабылдауда –
түскен ақпараттарды таңдау негізінде априорлық ықтималдықтарды кейінгі
қайта бағалаумен баламалық шешімдер жиынынан таңдау жасауға қабілетті
(апостериорлы ықтималдықтарды есептеу және талдау).
Өзін-өзі оқыту жүйесін құруға бейестік амал деп аталатын, қолданыстың қарапайым мысалын қарастырамыз.
Айталық S жүйесі түсетін Z ақпараттар негізінде екі H 0немесе H 1
баламалы шешімдерінің біреуін таңдауға тиіс. Тәжірибенің нәтижелері
57.
жөніндегі Z ақпараттан тәуелді H0 шешімінің дұрыстығының апостериорлыықтималдығы (3.6.7) Бейес формуласымен өрнектелуі мүмкін
P ( H 0 ) P(Z∨H 0 )
P( H 0 ∨Z )=
, (3.6 .8)
P ( H 0) P ( Z∨H 0 ) + P ( H 1 ) P ( Z∨H 1 )
мұндағы P ( H 0 ) , P ( H 1 ) – априорлық ықтималдықтар,
P( Z∨H 0 ), P( Z∨H 1)−¿шешімдердің шындыққа ұқсастығы.
P( H 0 ∨Z )≠ 0 -ге
(3.6.8) теңдігінің оң жағының алымын және бөлімін
бөлеміз. Шындыққа ұқсастықтар қатынасын белгілейміз:
P ( Z ∨H 1)
L=
.(3.6 .9)
P ( Z∨H 0 )
Сонда P( H 0 ∨Z ) үшін келесі өрнекті аламыз:
P ( H0)
P( H 0 ∨Z )=
.(3.6 .10)
P ( H 0) + LP ( H 1 )
Алынған (3.6.10) нәтижені талдаймыз. Айталық P(H 0 )=1 , P (H 1)=0.
Сонда апостериорлы ықтималдық P( H 0 ∨Z )=1.
Егер, керісінше, P(H 0 )=0 , P(H 1 )=1 , онда апостериорлы ықтимал-дық
P( H 0 ∨Z )=0.
Жоғарыда келтірілгендер мынаны көрсетеді, бірінші жағдайда
зерттелетін S жүйесі H 0 шешімді қабылдайды, ал екінші жағдайда H 1 шешімді
қабылдайды.
Сонымен, тәжірибелердің нәтижелері жөніндегі Z ақпаратының болуы
S жүйесінің шешімдерді қабылдау процесіне ешқандай әсер етпейді – жүйе
өзін-өзі оқуға тенденциялы емес, бұл жағдайда (3.6.9) шындыққа ұқсастық
қатынасының маңызы жоқ.
Егер (3.6.9) шындыққа ұқсастық қатынасы бірге тең болса, яғни L=1 ,
онда апостериорлы ықтималдық априорлы ықтималдыққа тең:
P ( H 0|Z ) =P ( H 0 ) ,(3.6 .11)
демек, түсетін Z ақпаратының шешімді қабылдауға әсері жоқ.
Шындыққа ұқсастық L қатынасының бірден айырмашылығы көп
болған сайын, апостериорлы және априорлы ықтималдықтардың айырмашылығы үлкен дәрежеде байқалады, түсетін Z ақпаратының H 0шешімін
қабылдауға әсері күшті болады. Тәжірибелердің нәтижелерін байқағанда
¿
ақпарат P ( H 0∨Z) жиілік түрінде және тәжірибелердің саны n өскен сайын
ықтималдықтар бойынша P( H 0 ∨Z ) ықтималдығына жинақталады. Демек, бұл
58.
жағдайда тәжірибелер нәтижелері жөніндегі Z ақпаратының бар болуышешімді қабылдауға әсерін тигізеді.
Сонымен, тәжірибелердің нәтижелері жөнінде Z ақпараты болмағанда S
жүйесі шешімдерді қабылдағанда тек қана P(H 0 ) және P(H 1 ) априорлық
ықтималдылықтарын басшылыққа алады. Тәжірибелердің нәтижелері
жөніндегі Z ақпаратын жинақтау шамасы бойынша S жүйесі өзін-өзі оқиды
және Z-тен тәуелді бола отырып, өзінің тәртібін жөндейді. «Өткен оқу»
жүйесі тәжірибелердің нәтижелерінен алынатын Z ақпаратынан тәуелді
P( H 0 ∨Z )
және
P( H 1∨Z) ықтималдықтарын
басшылыққа
алып
шешім
қабылдайды.
3.7. Тәжірибелерді қайталау
Тәжірибелерді қайталау, әрқайсысында ықтималдығы белгілі, кейбір А
оқиғасы орындалуы (немесе орындалмауы) мүмкін тәуелсіз оқиғалардың
тізбегі жүзеге асқандағы есептермен байланысты. Тәуелсіз тәжірибелер
жүргізгенде А оқиғасының дәл m рет пайда болуының ықтималдығын анықтау есебін шешеміз және осы ықтималдықты Pm , n (m=0 , … , n) арқылы
белгілейміз.
Pm , n ықтималдығын анықтаудың екі жағдайын қарастырамыз.
Бірінші жағдай. Тәуелсіз тәжірибелер бірдей шарттарда өткізіледі,
сондықтан әрбір тәжірибедегі А оқиғасының пайда болуының ықтималдығы
бірдей және мынаған тең P( A)= p, ал А оқиғасының пайда болмауының
ықтималдығы (қарама-қарсы Ā оқиғасының пайда болуы) мынаған тең
P( A)=1−q .Тәжірибелердің
(сынаулардың) осындай тізбегі Бернулли
сынаулары деп аталады. n тәжірибелерде А оқиғасының дәл m рет пайда
болуының Pm , n (m=0 , … , n) ықтималдығын анықтау керек.
Бернулли сынауларымен байланысты есептердің мысалдары
1. Үстелдің тегіс бетіне симметриялы монетаны n рет лақтыру өткізіледі. Әрбір
лақтыруда герб (цифр) пайда болуының ықтималдығы бірдей р=0,50. n рет
лақтырылғанда гербтің (цифрдің) дәл m рет (m=0,…,n) пайда болуының ықтималдығын
Pm , n анықтау керек.
2. t уақыт ішінде сенімділікке n біртипті агрегаттарды стендті сынаулардан өткізеді. Бір
агрегаттың тоқтаусыз жұмыс жасауының ықтималдығы P(t) белгілі және барлық
агрегаттар үшін бірдей. Барлық n агрегаттардың стендті сынаулардан сәтті
өтетіндігінің ықтималдығы Pm , n-ді анықтау керек.
3. Тирде нысанаға әрбір атуда бірдей қашықтықтан жеке көздеумен, n атыстармен ату
өткізіледі. Белгілі атқыш үшін «ондыққа» тигізудің ықтималдығы р шамасымен
59.
бағаланады. Атыстардың саны n болғанда «ондыққа» m рет тигізудің (m=0, 1, 2, ..., n)ықтималдығын анықтау керек.
n тәуелсіз тәжірибелерде А оқиғасының пайда болуының ықтималдығы
Pm , nмына өрнекпен (Бернулли формуласы) анықталатынын дәлелдейміз
Pm , n=C mn · pm ·q n−m , m=0 , … , n ,(3.7 .1)
мұндағы, C mn – n элементтерден m бойынша терулердің сандары (2.4.4),
(2.4.5),
p=P ( A ) – A оқиғасының бір (кез келген) тәжірибеде (сынауда) пайда
болуының ықтималдығы,
q=1− p – A оқиғасының бір (кез келген) тәжірибеде (сынауда) пайда
болмауының ықтималдығы.
Дәлелдеу үшін белгілеу енгіземіз: n тәуелсіз тәжірибелерде А
оқиғасының дәл m рет пайда болу оқиғасын Bm арқылы белгілейміз, яғни:
Pn (Bm )=Pm , n .
n тәжірибелерден серияларды көп рет қайта өткізгенде Bm оқиғасы әр
түрлі әдістермен пайда болулары мүмкін, әрбіреуінде А оқиғасы m рет пайда
болуға тиіс, ал қалған (n-m) ретте ол пайда болуға тиіс емес, қарама-қарсы Ā
оқиғасы пайда болуы тиіс. А оқиғасының пайда болуының бір фактісін
бірмен, ал Ā оқиғасының пайда болуының фактісін нөлмен белгілеп, Bm
оқиғаларының пайда болуларының мүмкіндіктері әдістерінің біреуін мына
түрде көрсетеміз
Bm , j= 1,1
,… , 1 , 0,0
, … , 0 , j=1, … , N .(3.7 .2)
⏟
⏟
{
m рет
n−m рет
}
Bm өрнектерінің басқа әдістері (3.7.2) өрнегімен тек қана нөлдің және
бірдің реттерімен өзгешеленеді, ал олардың сандары (m бірлер және (n-m)
нөлдер) өзгермейді. Осындай әдістердің саны орталарында m бірлер және (nm) нөлдер бар n элементтерден қайталанатын алмастырулардың санына тең
(2,4,6), басқаша n-нен m бойынша терулердің санына тең
N=P ( m , n−m )=
n!
=C mn .(3.7 .3)
m ! ( n−m ) !
Bmоқиғасының m бірліктер және (n-m) нөлдердің кез келген комбина-
циясында пайда болуының ықтималдығы оңай-ақ мынаған тең:
m
P ( B m , j )= p q
n−m
, j=1 , … , N .(3.7 .4)
Сонымен, (3.7.3) және (3.7.4) теңдіктерін ескеріп, соңында (3.7.1)
теңдігін аламыз:
m
m
Pm , n=C n p q
n−m
,m=0 , … ,n ,
60.
дәлелдеу керегі осы болатын.n
Pm , nықтималдықтары
(q + px ) Ньютон
биномының
х
тәуелсіз
айнымалысының дәрежелері бойынша жіктелуіндегі (2.5.6) коэффициенттері
секілді алынулары мүмкін:
n
n
m
n
m
( q+ px ) = ∑ C ( px ) q
m=0
n−m
n
=∑ Pm , n x m .(3.7 .5)
m=0
Сонымен, (3.7.5) теңдігінде биномдық коэффициенттер деп аталатын,
x тәуелсіз айнымалысының функциясы:
φ n ( x )=( q+ px )n ( 3.7 .6 )
Pm , n ізделінді ықтималдықтары үшін туындатқыш функция болады. (3.7.5)
теңдігіне x=1деп қойсақ, мынаны аламыз:
n
∑ Pm ,n=1.(3.7 .7)
m=0
Бұл қатынастың мағынасы қарапайым: А оқиғасының дәл m рет
(m=0,1,2,…,n) пайда болуынан құрылған n тәжірибелердің барлық мүмкін
нәтижелерінің ықтималдықтарының қосындысы бірге тең.
3.7.1-мысал. Әрқайсысында А оқиғасының пайда болуы ықтималдығы
p=0,60болатын төрт тәуелсіз тәжірибелер өткізіледі. А оқиғасының 3 реттен кем емес
пайда болуы ықтималдығын анықтау керек.
Шешуі. Төрт тәжірибелер өткізгенде А оқиғасының үштен кем емес пайда
болуының оқиғасын В деп белгілейміз. Сонда В оқиғасының пайда болу ықтималдығы А
оқиғасының үш рет немесе төрт рет пайда болулары ықтималдықтарының қосындысына
тең:
P ( B )=P3,4 + P 4,4 .
(3.7.1) формуласы бойынша есептің шешімін аламыз
P ( B )=C 34 p 3 q + p 4 =4 ∙ 0,603 ∙0,40+ 0,604 =0,476.
3.7.2-мысал. Монета 5 рет лақтырылады. Гербтердің түсуінің саны цифрлар
түсуінің санынан көп болуының ықтималдығы қандай?
Шешуі. Ізделінді оқиғаны – бес рет монетаны лақтырғанда гербтер түсуінің саны
цифрлар түсуінің санынан көп болу оқиғасын А деп белгілейміз. А оқиғасы орындалуы
үшін, бес рет (сәйкесінше, цифр 2, 1 немесе 0 болады) монетаны лақтырғанда гербтердің
саны 3, 4 немесе 5 болуы қажет. (3.7.1) формуласы бойынша:
3
3
2
4
4
5
3
2
4
P ( A )=P3,5 + P 4,5 + P5,5=C 5 p q +C 5 p q + p =10 ∙ 0,50 ∙ 0,50 +5 ∙ 0,50 ∙0,50+ ¿
+0,50 5=0,50.
61.
Екінші жағдай. Тәуелсіз тәжірибелер өзгеретін шарттардаөткізіледі, сондықтан i-ші тәжірибеде А оқиғасының пайда болуының
ықтималдығы мынаған тең P ( A i )= p i , ал А оқиғасының пайда болмауының
ықтималдығы (қарама-қарсы A оқиғасының пайда болуы) мынаған тең
P ( A i )=1− pi ¿ qi (i =1 ,… , n ) . n тәжірибелерде А оқиғасының дәл m рет пайда
болуының Pm , n ықтималдығын анықтау керек.
Өзгеретін шарттарда қайталанбалы тәжірибелер есептерінің мысалдары
1. Тапаншадан тәуелсіз атулармен нысанаға атыс өткізіледі. Әрбір атудан кейін атқыш
нысанаға бір қадам жасайды. Нысанаға тигізудің ықтималдығы әрбір кезекті атуда
өседі: p1 < p2 < p 3 <...< p n . Атыстың өзгеретін шарттарында n рет атуларда нысанаға дәл
m рет тигізудің Pm , nықтималдығын анықтау керек.
2. Техникалық құрылғы, t уақыт ішінде элементтері бір-бірінен тәуелсіз p1 , p2 , ... , pn
ықтималдықтарымен тоқтайтын n элементтерден құралған. t уақыт ішінде n элементтердің m элементтерінің (m=0,1,…,n) тоқтауының Pm , n ықтималдығын анықтау керек.
3. Бұйым n тәуелсіз жұмыс жасайтын бақылаушылар тарапынан бақылауға ұшырайды.
Бұйымды бірінші, екінші, ..., n-ші бақылаушыдан тексеруден өткізудің ықтималдықтары сәйкесінше мынаған тең: p1 , p2 , ... , pn . Бұйымның m бақылаушылардан (m=0,…,n)
сәтті өтуінің Pm , n ықтималдығын анықтау керек, бірақ барлық бақылаушылардың
бақылауынан өткендігінің Pn , n ықтималдығы жиі есептеледі.
Ізделінді Pm , nықтималдығы x тәуелсіз айнымалысының дәрежесі
бойынша
n
n
m
φ n ( x )=∏ ( q i+ p i x )= ∑ Pm ,n x (3.7 .8)
i=1
m=0
түрдегі туындатқыш функцияның жіктелуіндегі x m дәрежесінің коэффициентіне тең.
Нақтысында, (3.7.8.) функциясының құрамына кіретін барлық n
биномдарды қайта көбейтсек,
φ n ( x )=( q1 + p1 x ) ( q 2+ px ) … ( q n+ p n x ),
онда нәтиженің әрбір мүшесі міндетті түрде әрбір биномның бір элементінен
құрылады. Сондықтан x mдәрежесі коэффициентінің құрамында m әріптерден
әр түрлі p индекстермен әр түрлі құрамдағы комбинациялар болады, n
тәжірибелерде А оқиғасының m пайда болуына және (n-m) әріптер әр түрлі q
индекстерімен A оқиғасының (n-m) пайда болуына сәйкестенеді (А
оқиғасының пайда болмауы). Мысалы:
p , p ,... , p , ⏟
q , q , .., q . .
{⏟
}
1
2
m
m
m +1
m+2
n
n−m
Дербес жағдайда p1= p2=...= pn= p( q1=q2=...=qn =q) (3.7.8) туындатқыш
функциясы (3.7.5) Ньютон биномына айналады:
62.
nn
φ n ( x )=( q+ px ) = ∑ Pm , n x m .
m=0
3.7.3-мысал. Шарттары тәжірибеден тәжірибеге өзгеретін үш тәуелсіз тәжірибелер
өткізіледі. А оқиғасының бірінші тәжірибеде пайда болуының ықтималдығы
p1=0,40 , екіншісінде – p2=0,60 , үшіншісінде – p3=0,80. А оқиғасының үш тәуелсіз
тәжірибелерде дәл m рет (m=0, 1, 2, 3) пайда болуының Pm , 3ықтималдығын анықта.
Шешуі. (3.7.8) туындатқыш функциясын құрамыз және ізделінді Pm , 3
ықтималдығын осы функцияның x тәуелсіз айнымалысының дәрежесі бойынша
жіктелуіндегі x m-нің коэффициенттері түрінде есептейміз:
φ 3 ( x )=( 0,60+ 0,40 x ) ( 0,40+0,60 x ) ( 0,20+0,80 x )=¿
¿ 0,048+0,296 x +0,464 x 2 +0,192 x 3 .
Ізделінді ықтималдықтар мынаған тең:
P0,3 =0,048 , P1,3 =0,296 , P2,3=0,464 , P3,3 =0,192.
Шешімнің дұрыстығы (3.7.7) шартымен тексеріледі:
0,048+0,296 +0,464+0,192=1,000.
3.7.4-мысал. Радиолокациялық станцияның төрт операторы берілген секторда
әуедегі жағдайды бір-бірінен тәуелсіз талдайды. Әуедегі объектінің кедергі фонындағы
белгісін бірінші оператор p1=0,90 ықтималдықпен, екіншісі p2=0,80 ықтималдықпен,
үшіншісі – p3=0,70 ықтималдықпен, төртіншісі – p4 =0,60 ықтималдықпен біледі. Берілген
бақылау секторының ішінде әуе объектісінің пайда болуы жөнінде шешім қабылданады,
егер ең болмағанда, үш оператор объектіні білсе, бақылау секторының ішінде объектінің
пайда болуы жөніндегі шешімді қабылдаудың ықтималдығы қандай?
Шешуі. Берілген бақылау секторының ішінде әуе объектісінің пайда болуы
жөніндегі шешімді қабылдау оқиғасы А болсын. А оқиғасы орындалады, егер үш немесе
төрт оператор кедергі фонындағы объектіні білсе. Демек, А оқиғасының ықтималдығы
ықтималдықтардың қосындысына тең:
P ( A )=P3,4 + P 4,4 .
P3,4
және P4,4 ықтималдықтарын мына түрдегі туындатқыш функцияның
жіктелуіндегі x 3 және x 4 дәрежелерінің коэффициенттері түрінде анықтаймыз:
φ 4 ( x ) =( q 1+ p1 x )( q2 + p2 x ) (q ¿ ¿ 3+ p3 x) ( q 4 + p4 x )=¿ ¿
¿ ( 0,10+0,90 x ) ( 0,20+0,80 x )( 0,30+ 0,70 x ) ( 0,40+ 0,60 x).
x тәуелсіз айнымалысының дәрежесі бойынша:
φ 4 ( x ) =0,002+0,040 x+ 0,215 x 2 +0,440 x 3+ 0,302 x 4 .
63.
(3.7.7)-ні тексеру:0,002+0,040+ 0,215+ 0,440+0,302=1,000.
Pm , 4 ықтималдықтары мынаған тең:
P0,4 =0,002 , P1,4 =0,040 , P2,4 =0,215 , P3,4 =0,440 , P4,4 =0,302.
Ізделінді P ( A ) ықтималдығы мынаған тең:
P ( A )=0,440+ 0,302=0,742.
3.8. Ықтималдықтың аксиоматикалық анықтамасы
Ықтималдықтар теориясы математика ғылымы тәрізді шынайы әлемді
олардың нақты мазмұнынан алшақтай отырып, абстрактілі түрде, атап
айтқанда, бұл теория кездейсоқ құбылыстардың математикалық модельдерін
оқытады. Теорияның негізіне аксиомалар деп аталатын қандай да бір
нәтижелік жағдайлар салынады, ықтималдықтар теориясы аксиоматикалық
әдістерді қолданумен құрылады, ал қалған барлық жағдайлар аксиомалардың
логикалық салдары түрінде алынады.
Ықтималдықтар теориясын оқытудың әртүрлі әрекеттері көптеген
ғалымдармен жасалынды (қазірге дейін жасалуда), бірақ А.Н.Колмогоровтың
аксиоматикасы кеңінен өріс алды. 1933 жылы А.Н.Колмогоров ықтималдылық моделінің түсінігін қисынға келтіре тұжырымдады [10]. Осы тұжырым
теорияның тек қана классикалық бөлімдерін қамтымады, басқа да бөлімдердің дамуына жол ашты.
Дербес жағдайда, кездейсоқ процестер теориясы А.Н.Колмогоровтың
аксиомалары жүйесінің негізі келесі объектілерден құрылған (Ω , F , Р)
ықтималдылық кеңістігінің түсінігінде жатыр:
1) Ω – элементар оқиғалар деп аталатын ω элементтерінің жиыны. Ω
жиыны элементар оқиғалардың кеңістігі деп те аталды;
2) F – элементар оқиғалардың жиынының жиыншаларының жиынтығы. F жиынының А ∈ Ωэлементтері кездейсоқ оқиғалар деп аталады. F
жиыншаларының жүйесі σ -алгебра* болады;
3) Р – жиынның теріс емес және бірге дейін нормалданған функциясы:
P=P ( A ) .
64.
Барлық А оқиғалары үшін ықтималдық Pанықталған және келесіаксиомаларды қанағаттандырады:
*
F жиыншаларының жүйесі σ -алгебра деп аталады, егер осы жүйе келесі талаптарға жауап
берсе:
1) Ω ∈ F ;
2) ∅ ∈ F ( ∅−құ р жиын ) ;
3) F жүйесінің екі жиындарының бірігуі, қиылысуы және айырмасы осы жүйеге тиісті
болса (жатса).
4) F жүйесінің жиынының кез келген санаулы шоғырының бірігуі, қиылысуы және
айырмасы тағы да осы жүйеге тиісті болса.
1-аксиома. Әрбір А оқиғасына А оқиғасының ықтималдығы деп
аталатын теріс емес P ( A ) саны сәйкес келеді.
2-аксиома. P ( Ω )=1.
3-аксиома(ықтималдықтарды қосу аксиомасы). Егер А және В
оқиғалары қиылыспаса, онда P ( A + B )=P ( A ) + P ( B ) .
4-аксиома (қосудың кеңейтілген аксиомасы). Егер A1 , A 2 ,… , An ,… –
қос-қостан үйлесімсіз оқиғалар болса, онда
P ( A 1 + A 2 +...+ An +... ) =P ( A 1 )+ P ( A 2 ) +...+ P ( A n ) +. ..
1-4 аксиомаларын қанағаттандыратын ( Ω, F , P) объектілерінің жиынтығы ықтималдылық кеңістігі деп аталады.
Қарапайым ақырлы ықтималдылық кеңістік келесі түрде құрылады.
Кез келген Ω=( ω1 , … , ωn } ақырлы жиын үшін әрбір ω l элементар оқиғасына
сәйкес pi−¿ элементар ықтималдық анықталады, p1 + p2+ ...+ p n=1. F
жиыншаларының жүйесі үшін Ω жиынының А жиыншаларының жиынтығы
қабылданады.
Аксиомалардың жүйесі қарама-қайшылықта болмайды. Осыны
көрсету үшін келесі мысалдарды қарастырамыз.
3.8.1-мысал. Айталық, Ω жалғыз ω элементінен тұрсын, сонда F жиыншаларының
жүйесі екі элементтен тұрады: F және ∅құр жиыннан. Сонда P(Ω )=1, P(∅)=1 және P(
Ω+∅) = P(Ω ) + P(∅), яғни аксиомалардың барлық шарттарын қанағаттандырады.
65.
3.8.2-мысал. Айталық, Ω ақырлы санды элементтер жиынынан тұрсын. Мысалы,ойын сүйегін лақтырғандағы элементар оқиғалар кеңістігі мына түрде болады
Ω={ ω1 , ω2 , ω3 , ω 4 , ω5 , ω6 } ={ 1,2,3,4,5,6 } .
F жүйесі келесі жиыншалардан тұрады: A1= {∅ } , A2= { ω1 } , … , A7 ={ ω 6 } , A8 ={ω 1 , ω 2
} және т.б. (яғни бір бос жиынша, бір элементтерден тұратын 6 жиынша, екі
элементтерден тұратын 15 жиынша және т.б., барлығы 72 жиынша). Жиыншалардың
әрқайсысы үшін P( Ai ) ықтималдығы анықталуы мүмкін; P ( Ω )=1 кез келген үйлесімсіз
оқиғалар Ai , A jжұптары үшін мына теңдік дұрыс P ¿ + A j ¿=P ( A i ) P( A j) ,яғни бұл
жағдайда да барлық аксиомалардың шарттары қанағаттандырылады.
Аксиомалар жүйесі толық болмайды. Осы шарттың болуы әр түрлі
қолданбалы сұрақтарды шешкенде ықтималдылық кеңістігі де әр түрлі
анықталуы мүмкін. Мысалы, симметриялық ойын сүйегін лақтырғанда,
P ( ω1 ) =P ( ω2 ) =...=P ( ω 6 )=1/6 . Бірақ біз симметриялы емес, дұрыс емес ойын
сүйегін
қарастыруымыз
мүмкін,
ол
үшін
мысалы,
P ( ω1 ) =P ( ω2 ) =1/6 , P ( ω 3 )=P ( ω 4 ) =1/4 , P ( ω 5 )=P ( ω 6 )=1/12 .
Кездейсоқ оқиғалар кездейсоқ оқиғаларға қолданылатын амалдар –
сәйкес жиындарға қолданылатын амалдар жиыны сияқты анықталған.
Көптеген теориялық-ықтималдылық түсініктері белгіленеді, бірақ, басқа
терминдермен (5-кесте).
5-кесте
Белгілеулер
Ω
Жиындар теориясы
Жиын, кеңістік
Терминдер
Ықтималдық теориясы
Элементар оқиғалар кеңістігі,
ақиқат оқиға
ω
Жиынның элементі
Элементар оқиға
A,B
Α , Β жиыншалары
Α , Β кездейсоқ оқиғалары
Α∪Β
Α ж ә не Β жиындарының бірігуі
Α ж ә не Β үйлесімді кездейсоқ
оқиғаларының қосындысы
Α ∩ Β= ΑΒ
Α жә ә не Βжиындарының
қиылысуы
Α ж ә не Β кездейсоқ
оқиғаларының көбейтіндісі
А жиынының толықтырылуы
Α оқиғасына қарама-қарсы
оқиға
Α
Α−Β
Α жә ә не Β жиындарының
айырмасы
∅
Α ж ә не Β оқиғаларының
айырмасы
Мүмкін емес оқиға
66.
ΑΒ= Α ∩ Β=∅Α=Β
Α ж ә не Β оқиғалары үйлесімсіз
Құр жиын
Α ж ә не Β жиындары қиылыспайды
(ортақ элементтері жоқ)
Α ж ә не Β оқиғалары тең
мүмкіндікті
Α жә ә не Βжиындары тең
Α⊂Β
Α оқиғасы В оқиғасын
ілестіреді
Α ж ә не Β жиынының жиыншасы
Салдарлар (тікелей тұжырымдалған 1-4 аксиомаларынан шығады):
1. A+ Α=Ω теңдігінен және 2-, 3-аксиомаларынан шығады:
P ( A ) + P ( Α )=1 ,
P ( Α )=1−P ( A ) .
Дербес жағдайда, Ω=∅ болғандықтан,
P ( ∅ )=1−P ( Ω ) =0.
2. A оқиғасы қандай болса да, ол үшін:
0 ≤ P (A )≤ 1.
3. Егер А оқиғасы В оқиғасын ілестірсе, онда:
P( A) ≤ P ( B ) .
4. 3-аксиомадан қосу теоремасы шығады: егер A,B,…,N – қос-қостан
үйлесімсіз оқиғалар болса, онда
P ( A + B+…+ N ) =P ( A )+ P ( B ) +…+ P ( N ) .(3.8 .1)
5. Айталық А және В кез келген оқиғалар
A+ B= A + ( B− AB ) ,
B= AB+ ( B− AB ) .
өрнектерінің оң жағындағы қосылғыштар үйлесімсіз оқиғалар (3.8.1-суретін
қараңыз) болғандықтан, онда (3.8.1) қосу теоремасына сәйкес аламыз:
P ( A + B )=P ( A ) + P ( B− AB ) , ( 3.8 .2 )
P ( B )=P ( AB ) + P ( B− AB ) . (3.8.3)
(3.8.3) теңдігінен P ( B− AB )-ны өрнектеп және алынған өрнекті (3.8.2)
теңдігіне қойып, кез келген оқиғалар үшін қосу теоремасын аламыз:
P ( A + B )=P ( A ) + P ( B )−P ( AB ) . ( 3.8.4 )
6. P ( AB ) мәнінің теріс еместігіне сәйкес,
P ( A + B)≤ P ( A )+ P (B )
теңсіздігі орындалады.
67.
7. А оқиғасы орындалғандағы В оқиғасының шартты ықтималдығыанықтама бойынша (п.1.4-ті қараңыз) мынаған тең:
P( AB )
,(3.8 .5)
P( A)
мұндағы, P( A)>0.
P ( B∨ A )=
(3.8.5) теңдігінен тікелей шығады:
P ( AB ) =P ( A ) ∙ P ( B∨A ) .(3.8 .6)
Индукция бойынша көбейту теоремасын аламыз:
P ( A 1 A 2 … A n )=P ( A 1 ) P ( A 2 ¿ A1 ) P ( A 3| A1 A 2 ) … P ( A n∨ A1 A 2 … A n−1 ) .
Шартты ықтималдықтар үшін келесі қасиеттер жеңіл дәлелденеді:
P ( A|B ) ≥ 0 ;
P ( A| A ) =1;
P ( Ω| A ) =1.
Өзара үйлесімсіз В және С оқиғалары үшін мына теңдік дұрыс
P ( B+C∨ A )=P ( B∨ A ) + P ( C∨A ) .
8. Үйлесімсіз оқиғалардың толық тобын құрайтын оқиғалардың
жиынын A1+ A2 +...+ An =Ω ,сол сияқты кез келген В оқиғасын қарастырамыз.
Мына теңдік орындалады:
B=B Ω=B ( A1 + A2 +…+ A n )=B A 1 + B A 2+ …+B A n ,
сонда
P ( B )=P ( B A1 ) + P( B A2 )+...+ P ( BA n) .
Бірақ (3.1.4) теңдігіне сәйкес, P ( B A i) =P ( B A i) P(B∨A i),
ықтималдықтар формуласы шығады
бұдан
толық
P ( B )=P( A1 ) P( B∨A 1)+ P( A 2) P(B∨ A2 )+...+ P( An )P(B∨A n ).(3.8 .7)
9. (3.8.6) формуласынан және осы формулаға ұқсас
P ( AB ) =P ( B ) P ( A∨B )
формуладан Бейес теоремасының математикалық тұжырымын аламыз:
P ( A∨B )=
P ( A ) P ( B∨ A )
.(3.8 .8)
P(B)
68.
А. Н. Колмогоровтың аксиомалар жүйесінен жоғарыда қарастырылғанықтималдықтар теориясының жағдайлары дедуктивті әдіспен дәлелденетіні
көрініп тұр.
4-ТАРАУ
Кездейсоқ шамалар
4.1. Кездейсоқ шаманың түсінігі
Шама кездейсоқ шама деп аталады, егер тәжірибенің нәтижесінде осы
шама мүмкін мәндерінің жиынынан сол немесе алдын ала белгісіз мәнді
қабылдаса. Кездейсоқ шамаларды латын әліпбиінің X , Y , Z ,U , V , … , бас
әріптерімен, грек әліпбиінің А , В , Г , Ф , Ω , … және басқа әліпбилердің, ал
кездейсоқ шамалардың мүмкін мәндерінің сәйкесінше кіші әріптермен
x , y , z , u , υ , … , α , β , γ , φ , ω , …және т.б. Сонымен қатар кездейсоқ шамаларды
X 1 , X 2 , X 3 , …және олардың мәндерін x 1 , x 2 , x 3 ,…индекстерімен белгілеулер
қолданылады. Келешекте «кездейсоқ шама» термині орнына қысқаша КШ
деп қолданамыз.
Нөмірлеуге болатын, бірнеше интервалдармен бөлінген мәндерді
қабылдайтын шаманы дискретті шама деп атайды (4.1.1-сурет) .
Дискретті кездейсоқ шамалардың мысалдары
1. Ойын сүйегін бір рет лақтырғанда түсетін ұпайлардың саны – Х кездейсоқ
шамасы.
Оның мүмкін мәндерінің жиыны θ х :
θ х ={ x 1 , x 2 , x 3 , x 4 , x 5 , x 6 }= {1 , 2 ,3 , 4 , 5 ,6 } ,
x k −k ұпайлардың пайда болуы, k =1,2 , … ,6 , x k =k .
4.1.1-сурет. Дискреттік кездейсоқ шама
69.
4.1.2-сурет. Үзіліссіз кездейсоқ шама2. Үш рет оқ атқанда нысанаға тию саны – Z кездейсоқ шамасы.
Оның мүмкін мәндерінің жиыны θ z :
θ z= { z0 , z 1 , z 2 , z 3 }= { 0,1,2,3 } ,
z 0 – біреуі де тимейді, z 0=0 ,
z 1– біреуі тиеді, z 1=1 ,
z 2 – екеуі тиеді, z 2=2 ,
z 3−¿ үшеуі тиеді, z 3=3.
3. t уақыт ішінде төрт агрегаттарды сынағанда тоқтайтын агрегаттардың саны – N
кездейсоқ шамасы.
Оның мүмкін мәндерінің жиыны θn :
θn ={ n0 , n1 , n2 , n3 , n4 }={ 0 , 1 ,2 , 3 , 4 } ,
n j−¿ j агрегаттардың тоқтауы, j=0,1 , … , 4 , n j= j .
Мүмкін мәндері қандай да бір x min-нен x max-ге дейінгі аралықты үзіліссіз
толтыратын шаманы үзіліссіз кездейсоқ шама деп атайды (4.1.2- сурет).
Үзіліссіз кездейсоқ шамалардың мысалдары
1. Тоқтаусыз жұмыс істейтін техникалық шамалар құрылымының бірінші тоқтағанға
дейінгі уақыты - кездейсоқ шама Т. Оның мүмкін мәндерінің жиыны:
θr ∈ [ t min=0; t max ] .
2. Атудың қатесі – снарядтың (оқтың, зымыранның) түсу жүйесінен нысананың центріне
дейінгі қашықтық – кездейсоқ шама R. Оның мүмкін мәндерінің жиыны:
θr ∈ [ r min =0 ; r max ] .
3. Жылдамдықты өлшеу қателігі – кездейсоқ шама ∆ υ . Оның мүмкін мәндерінің жиыны:
θ ∆ υ ∈ [ ∆ υ min ;∆ υ max ] .
Кездейсоқ шама кездейсоқ оқиға сияқты тәжірибенің элементар
нәтижелерінің жиынында құрылады. Үш монетаны лақтыру мысалын
қарастырамыз. Тәжірибе нәтижелерінің жиынын үш монеталардағы гербтердің (Г) және цифрлардың (Ц) комбинацияларының түрінде өрнектейміз:
Ω= ГГГ
ЦГЦ , ЦЦГ
⏟ , ГГЦ
⏟ , ГЦГ
⏟ , ЦГГ
⏟ , ГЦЦ
⏟ ,⏟
⏟ , ЦЦЦ
⏟, ,
{
ω1
ω2
ω3
ω4
ω5
ω6
ω7
ω8
}
70.
мысалы, ω 2={ГГЦ } үш монеталарды лақтырғанда бірінші монетада герб,екінші монетада герб және үшінші монетада цифр түскендігін көрсетеді.
Y кездейсоқ шамасын – үш монеталарды лақтырғанда гербтер түсуінің
санын қарастырамыз. θ y мәндерінің жиыны:
θ y ={ 0,1,2,3 } , y k =k , k =0,1,2,3.
Y кездейсоқ шамасының мүмкін мәндері және тәжірибенің нәтижелерін
салыстырып, тәжірибенің нәтижелері ω i (i=1 , … ,8)және y k ( k =0 , … ,3 ) Y КШ
мәндерінің арасындағы сәйкестікті байқаймыз:
y 0=0 ω8 ,
y 1=1 ω5 + ω6 +ω 7 ,
y 2=2 ω 2+ ω3 +ω 4 ,
y 3=3 ω 1 .
4.2. Кездейсоқ шаманың үлестіру заңы
Кездейсоқ шаманың мүмкін мәндерінің және осы мәндер ықтималдықтарының арасындағы сәйкестікті тағайындайтын қандай да p(x) функциясын
X кездейсоқ шамасының үлестіру функциясы деп атайды.
Айталық дискретті X КШ-ның мүмкін мәндерінің жиыны болады
θ x ={ x 1 , x 2 ,… , x n } ,
ал осы мәндердің ықтималдықтары сәйкесінше мынаған тең:
p ( x 1) , p ( x 2) , … , p ( x n ) ,
солай,
n
∑ p ( x i )=1 ,
i=1
толық топты құрайтын (3.3.1), Ai= ( X=x i ) , i=1 , … ,n үйлесімсіз оқиғалардың
қосындысы секілді, олардың қосындысы бірге тең. Сонымен бірге тең
ықтималдық қосынды Х КШ мәндерінің арасында анықталған түрде
үлестіріледі.КШ Х-тің мәндерінің ықтималдықтарын беру
P ( A i )=P ( X=x i )= p ( x i ) ,i=1, … , n ,(4.2.1)
оның үлестіру заңын көрсету болады.
КШ Х үлестіруінің заңын берудің бірнеше түрі болады:
71.
1. үлестіру қатары;2. үлестіру функциясы – интегралдық заң;
3. ықтималдық (үлестіру) тығыздығы –дифференциалдық заң.
Үлестіру қатары
Х дискретті кездейсоқ шамасының үлестіру заңының қарапайым түрі
кесте болады, кестеде Х-тің мүмкін мәндері және оларға сәйкес
ықтималдықтар жазылған (6- кесте).
6-кесте
xi
x1
x2
x3
p ( x i)
p ( x 1)
p ( x 2)
p ( x3)
…
xn
p ( xn )
…
6-кесте КШ Х-тің үлестіру қатары деп аталады. Үлестіру қатарының
геометриялық кескінделуі үлестіру көпбұрышы деп аталатын түрде
кескінделеді (4.2.1- сурет): абсцисса oсі бойынша КШ-ның мүмкін мәндері
x 1 , x 2 , … , x n , ал ордината oсі бойынша осы мәндердің ықтималдықтары
p ( x 1) , p ( x 2) , … , p ( x n )салынады, көрнекі болуы үшін ( x i , p ( x i ) ) нүктелері түзулердің
кесінділерімен қосылады. Үлестіру көпбұрышы КШ Х-ті толығымен
сипаттайды және үлестіру заңының кескінделуінің бірі болады.
4.2.1- cурет. Үлестіру көпбұрышы
4.2.1-мысал. А оқиғасы әрқайсысында p=0,60 ықтималдықпен пайда болатын, екі
тәуелсіз сынаулар өткізіледі. А оқиғасының пайда болу сандары Х кездейсоқ шамасының
үлестіру заңын құрамыз.
Шешуі. Х кездейсоқ шамасының x 0=0 , x 1=1 , x 2=1 қабылдайтын мәндеріне
Бернулли формуласымен есептелетін ықтималдықтар (Бернулли сынауларының
72.
формуласын қолданамыз, бірдей шарттардағы екі тәуелсіз тәжірибелер болғандықтан(3.7.1)):
2
2
p0=P ( X=x 0 )=q =0,40 =0,16 ,
p1=P ( X =x 1) =2 pq=2 ∙ 0,60∙ 0,40=0,48 ,
p2=P ( X =x 2) = p2=0,60 2=0,36 ,
тексеру: 0,16+ 0,48+0,36=1,00.
Үлестіру қатары келесі түрдегі 7-кестеде көрсетілген
7-кесте
xi
p ( x i)
0
0,16
1
0,48
2
0,36
4.2.2-сурет. Үлестіру көпбұрышы
Үлестіру функциясы
Кездейсоқ шама Х қандай да бір бекітілген х мәндерінен кіші (Х< x )
мәндерді қабылдағандағы оқиғаның ықтималдығы КШ Х-тің F ( x)үлестіру
функциясы деп аталады
F ( x )=P ( X < x ) .(4.2 .2)
F ( x ) үлестіру функциясының графиктегі кескінделуі (4.2.3) суретінде
көрсетілген: КШ Х абсцисса осінде х нүктесінің сол жағында жататын
мәндерді қабылдайды – үлестіру функциясы сол жақта үзіліссіз.
73.
4.2.3-сурет. Үлестіру функциясының мүмкін мәндеріҮлестіру функциясының қасиеттері (4.2.3-, 4.2.4-суреттерді қараңыз)
1. F (−∞ )=P ( X ←∞ )=P ( ∅ )=0 ,яғни КШ Х-тің (−∞ )-тен сол жаққа түсуінің
ықтималдығы – мүмкін емес оқиғаның ықтималдығы – нөлге тең.
2. F ( + ∞ ) =P ( X <+∞ )=P ( Ω ) =1, КШ Х-тің барлық сан осіне түсуінің
ықтималдығы – ақиқат оқиғаның ықтималдығы бірге тең.
3. Егер x 2< x1 , F ( x 2 ) ≥ F ( x 1 )орындалады, яғни үлестіру функциясы аргумент
х-тен кемімейтін функция.
Үлестіру функциясының үшінші қасиетін дәлелдеу үшін абсцисса
осінен x 1< x2 (4.2.4-суретін қараңыз) нүктелерін аламыз және төмендегі
оқиғаларды қарастырамыз
A=( X < x 1 ) ,
B=( x 1 ≤ X < x 2 ) , (4.2 .3)
C=( X < x 2 ) ,
}
өзара мына қатынаспен байланысқан
A+ B=C .
4.2.4-сурет. А, В, С оқиғаларының қатынастары
Ықтималдықтарды қосу теоремасына (3.2.4) сәйкес, А және В
оқиғалары қосындысының ықтималдығы олардың ықтималдықтарының
қосындысына тең:
P ( A ) + P ( B )=P (C ) .(4.2 .5)
(4.2.3) теңдіктерін (4.2.5) теңдігіне қойып, аламыз:
74.
P ( X < x 1 ) + P ( x1 ≤ X < x 2 )=P ( X < x 2 ) .(4.2 .6)Үлестіру функциясының анықтамасын (4.2.2) ескеріп, (4.2.6) теңдігін
былай жазамыз
F ( x 2 )−F ( x 1) =P ( x1 ≤ X < x 2 ) ≥ 0 ,( 4.2.7)
үлестіру функциясының үшінші қасиеті дәлелденеді.
(4.2.7) формуласында x 1-ді α -ге, x 2-ні β -ға алмастырып, аламыз:
P ( α ≤ X < β )=F ( β ) −F ( α ) .( 4.2 .8)
(4.2.8) формуласы КШ Х-тің α және β аралығындағы кесіндіге түсуінің
ықтималдығын осы кесіндідегі (дәлірек, жартылай интервал) үлестіру
функциясының өсімшесі түрінде өрнектейді. Бұл 4.2.6-суретінде көрсетілген.
(4.2.8) формуласы басқаша мына түрде жазылады:
P¿
Алдағы уақытта «үлестіру функциясы» термині үшін қысқаша «ҮФ»
деп жазуды қолданамыз.
4.2.2-мысал. 4.2.1-мысалы үшін ҮФ-ның мәндерін есептейміз және оның графигін
саламыз. Басында F ( x ) ҮФ мәндерін X =x i сипаттамалық нүктелер үшін есептейміз, содан
кейін графикте функцияны тұрғызамыз (4.2.5-сурет):
F ( 0 )=P ( X <0 ) =0 ;
F ( 1 )=P ( X < 1 )=P ( X=0 )=0,16 ;
F ( 2 ) =P ( X< 2 )=P ( X=0 ) + P ( X=1 ) =0,16+0,48=0,64 ;
F ( 2+ ε )=P ¿
¿ 0,64+ 0,36=1,00 , м ұ нда ε> 0.
ҮФ F ( x )-тің есептелген мәндерінің нәтижелерін 8-кестеде жазамыз.
8-кесте
xi
F ( xi )
0
0
1
0,16
2
0,64
2+ε
1,00
75.
4.2.5-сурет.Үлестіру функциясының графигіx iнүктесіндегі ҮФ-ның өсімшесі p ( x i) ықтималдығына тең – осы нүктеде
ҮФ F ( x ) p ( x i ) шамасына секіріс жасайды. Нақтысында, (4.2.9) формуласында
α =β деп аламыз, сонда:
P ( X=α ) =lim ( F ( β )−F (α ) )=0.(4.2 .10)
α→ β
КШ Х үзіліссіз болған жағдайда P ( X=α ) ықтималдығы нөлге тең, бұл
(4.2.10) теңдігінен шығады.
Х ҮФ талдауынан және (4.2.2) мысалдан шығады, аргументтің мәні
үлкейген сайын ҮФ-ның мәні өседі – КШ Х-тің мәндерінің ықтималдықтары
қосылады. Осы негізде F(х) ҮФ КШ Х-тің интегралдық үлестіру заңы деп
аталады.
КШ ш-тің мәндерінің саны өскенде F(х) ҮФ графигінде секірмелердің
саны өседі, бірақ осы секірмелердің шамасы азаяды. n → ∞ болса шегінде КШ
Х-тің мәндерінің саны шексіз өседі, секірістердің шамалары нөлге ұмтылады
және үзіліссіз КШ ҮФ үзіліссіз функция болады (4.2.6-сурет).
Қорытындыда мынаны ескертеміз, үлестіру функциясы универсал
функция, өйткені дискреттік және үзіліссіз кездейсоқ шамалар үшін де
табылады. Бірінші жағдайда (дискретті КШ) үзілісті секірмелі өзгеретін
функция, х iнүктелерінде р ( х i) ықтималдықтарына
тең
секірістермен
(секірмелермен) өзгереді – үзілісті функция, ал екінші жағдайда үзіліссіз
функция. Екі жағдайда ҮФ нөлден бірге дейінгі шектерде өзгереді.
76.
4.2.6-сурет.Үзіліссіз үлестіру функциясыЫқтималдық тығыздығы
Х кездейсоқ шамасы ықтималдығының тығыздығы (үлестіру
тығыздығы) f(х) тек қана үзіліссіз кездейсоқ шамалар үшін болады және Х
кездейсоқ шамасының кесіндіге түсу ықтималдығының осы кесіндінің
ұзындығына қатынасының, соңғысы (кесіндінің шегі) нөлге ұмтылғандағы
шегі түрінде анықталады:
P ( X ∈ [ x , x+ ∆ x ] )
.(4.2 .11)
∆x
∆x →0
f ( x )= lim
X кездейсоқ шамасының [ x , x +∆ x ] кесіндісіне түсуінің ықтималдығын
(4.2.8) формуласы бойынша осы кесіндіде F(х) үлестіру функциясының
өсімшесі түрінде (кесіндінің оң жақ нүктесіне дейінгі дәлдікпен)
өрнектейміз:
F ( x + ∆ x ) −F ( x ) dF ( x )
=
=F ' ( x ) .(4.2 .12)
∆x
dx
∆x →0
f ( x )= lim
f ( x ) тығыздығы
F ( x )үлестіру
Ықтималдықтың
функциясының
туындысына тең. Осыдан «үлестірудің дифференциалдық заңы» атауы
шығады.
Ықтималдық тығыздығының қасиеттері
1. Ықтималдықтың тығыздығы – x аргументінен теріс емес функция:
f ( x ) ≥ 0.(4.2 .13)
2. Ықтималдық тығыздығының шексіздіктердегі интегралы бірге тең:
∞
∫ f ( x ) dx=1 .(4.2.14)
−∞
77.
Бірінші қасиет (4.2.11) анықтамасынан шығады: алымында шегінденөлден бірге дейін жататын оқиғаның ықтималдығы тұр, ал бөлімінде
кесіндінің ұзындығы – оң шама.
Екінші қасиетті дәлелдеу үшін ықтималдықтың элементі түсінігін
енгіземіз. (4.2.11) теңдігінің сол және оң жақтарын ∆ x шамасына көбейтеміз
және мына түрде жазамыз:
p ( X ∈ [ x , x +∆ x ] ) ≈ f ( x ) ∆ x .( 4.2.15)
f ( x ) ∆ x көбейтіндісі ықтималдықтың элементі деп аталады және
сандық мәні (∆ x -ке дейінгі дәлдікпен) X кездейсоқ шамасының [ x , x +∆ x ]
кесіндісіне түсуінің ықтималдығына тең. 4.2.7-суретте кездейсоқ
шамасының үлестіру қисығы деп аталатын f ( x ) ықтималдық тығыздығының
типтік графигінің геометриялық кескіні келтірілген.
4.2.7-сурет. Ықтималдықтың элементі
Ықтималдықтың элементі шамамен, ∆ x кесіндісіне тірелетін х
нүктесіне жанасатын элементар төртбұрыштың (4.2.7-суретте штрихталған) ауданына тең. Тік төртбұрыштың биіктігі f ( x )-ке тең. X кездейсоқ
шамасының [ α , β ] кез келген кесіндіге түсуінің ықтималдығы шамамен осы
кесіндідегі ықтималдықтың элементтерінің қосындысына тең екендігі
қарапайым белгілі (4.2.8-сурет):
p ( X ∈ [α , β ]) ≅
∑
f ( x ) ∆ x ,(4.2 .16)
∆ x ∈[ α , β ]
ал ∆ x →0 шегінде кездейсоқ Х шамасының ықтималдық тығыздығы α -ден β ға дейінгі шектердегі интегралға тең
β
p ( X ∈ [ α , β ])=∫ f ( x ) dx .( 4.2.17)
α
Кесіндіге түсудің ықтималдығы сол жағынан және оң жағынан α , β
нүктелеріндегі ординаталармен шектелген үлестірудің қисығы астындағы
ауданмен геометриялық кескінделеді (4.2.8-суретте штрихталған).
78.
4.2.8-сурет. Кесіндіге түсу ықтималдығыЕнді ықтималдықтың тығыздығының екінші қасиетін (4.2.14)
дәлелдеуге ораламыз. (4.2.17) формуласында α =−∞ , β=+∞ деп аламыз. Х
кездейсоқ шамасының шексіз кесіндіге (барлық сан осіне) түсуінің
ықтималдығы бірге тең ақиқат оқиғаның ықтималдығы екендігі қарапайым
белгілі:
∞
P ( x ∈ (−∞ , ∞ ) )= ∫ f ( x ) dx=P ( Ω )=1.
−∞
Соңында F ( x )үлестіру функциясын f ( x ) ықтималдықтың тығыздығы
арқылы өрнектейміз, ол үшін (4.2.2) үлестіру функциясының анықтамасын
және (4.2.17) формуланы қолданамыз:
x
F ( x )=P ( X ∈ x ) =P (−∞< X < x )= ∫ f ( u ) du .(4.2.18)
−∞
(4.2.18) қатынасына негізделген F ( x ) үлестіру функциясының геометриялық кескінделуі 4.2.9-суретінде көрсетілген: f ( x ) үлестіру қисығының
астындағы штрихталған аудан үлестіру функциясын көрсетеді.
4.2.9-сурет. Үлестіру функциясы
4.3. Кездейсоқ шаманың моменттері және сандық сипаттамалары
Біз жоғарыда кездейсоқ шамалардың толық сипаттамаларымен –
олардың үлестіру заңдарымен таныстық. Бірақ көптеген практикалық
есептерде кездейсоқ шамалардың кеңейтілген сандық сипаттамаларын білу
79.
жеткілікті. Мұндай сипаттамалар олардың (кездейсоқ шамалардың) ең көпмаңызды қасиеттерін – кездейсоқ шаманың орта мәнін, кездейсоқ шаманың
орташа мәнге қарағанда шашырауын және көптеген басқа сипаттамаларын
көрсетеді.
Кездейсоқ шаманың математикалық күтімі
Х кездейсоқ шамасының орта мәнінің сипаттамасы – оның
математикалық күтімі* (қысқаша МК). Математикалық күтімді қысқаша
МК деп жазамыз. МК-ді M [ X ] немесе mx символдарымен белгілейміз.
Дискреттік КШ үшін МК:
n
M [ X ] =∑ x i p( x i )(4.3 .1)
i=1
формуламен анықталады.
КШ-ның x i мәндерінің осы мәндердің p( x i) ықтималдықтарына
көбейтінділерінің қосындысы дискретті X КШ-ның математикалық күтімі
деп аталады.
Егер (4.3.1) қосындысы жинақты болса, онда кездейсоқ шаманың МК
табылады, қарсы жағдайда МК табылмайды.
4.3.1-суретінде МК-нің механикалық интерпретациясы көрсетілген.
xi
Абсцисса
осінде
координаталарымен
нүктелері
белгіленген,
p1 + p2+ …+ pn=1 теңдігін қанағаттандыратын шартты pi (i=1 , … , n) массалары
осы нүктелерге сәйкесінше шоғырланған. (4.3.1) формуласымен
анықталатын, осындай қойылымдағы Х кездейсоқ шамасының МК p1 , p2 , … , p n
салмақтарымен x 1 , x 2 , … , x n материалдық нүктелерінің жүйесінің ауырлық
центрінің абциссасы болады.
Егер Х дискретті кездейсоқ шамасын ықтималдықтары сәйкесінше
p1 , p2 , … , p n-ге тең болатын мүмкін x 1 , x 2 , … , x n мәндерімен қарастырсақ, онда
(4.3.2) формуласымен есептелетін X кездейсоқ шамасының орта салмағы
математикалық күтім болады:
x=
x 1 p1 + x 2 p2 +...+ x n pn n
=∑ x i pi =M [ X ] .(4.3.2)
p
+
p
+...+
p
1
2
n
i=1
⏟
1
4.3.1-сурет. Математикалық күтімнің механикалық интерпретациясы
80.
4.3.1-мысал. Х КШ-ның үлестіру заңы 9-кестеде көрсетілген түрде болады.9-кесте
xi
1
0,20
p= p (xi )
2
0,30
3
0,30
4
0,20
Х КШ-ның МК табу керек.
Шешуі. (4.3.1) формуласымен есептейміз:
4
mx =∑ xi p(x i)=1∙ 0,20+2 ∙ 0,30+3∙ 0,30+ 4 ∙ 0,20=2,50.
i=1
(4.3.1) формуласында X кездейсоқ шамасының x i дискреттік мәндерін x
үзіліссіз мәндеріне, x i мәндерінің p( x i) ықтималдықтарын f ( x i) dx
ықтималдықтың элементіне алмастырып және интегралдық қосындының
шегіне көшіп, үзіліссіз X кездейсоқ шамасының математикалық күтімі үшін
өрнекті аламыз:
∞
M [ X ] =∫ xf ( x ) dx .(4.3 .3)
−∞
4.3.2-мысал. 4.3.2-суретінде көрсетілген X кездейсоқ шамасының үлестіру заңы
мына түрде жазылады:
1
f ( x )= b−a , x ∈ [ a , b ] ,
0 , x ∉ [ a ,b ] .
{
(4.3.3) формуласымен X кездейсоқ шамасының математикалық күтімін табамыз:
b
2
2
1
b −a
a+b
=
.(4.3 .4)
∫ xdx= 2(b−a)
b−a a
2
Х КШ МК [a , b] кесіндісінде тұрғызылатын төртбұрыштың центрі болады
(4.3.2-суретте mx нүктесімен белгіленген).
M [ X ]=
4.3.2-сурет. Бірқалыпты үлестіру
81.
4.3.3-сурет. Үлестірудің модасы4.3.4-сурет. Үлестірудің медианасы
4.3.3- және 4.3.4-суреттерінде X кездейсоқ шамасы үлестіруі қисығының модасы ( M ) және мединанасы ( Me ) көрсетілген.
X кездейсоқ шамасының f max ( x )-ке сәйкес ең үлкен ықтималдық мәні
мода деп аталады:
P ( X < Me )=P ( X > Me ) ,( 4.3.5)
теңдігі орындалатын, яғни x=Me нүктесінің сол жағындағы аудан, осы
нүктенің оң жағындағы ауданға тең болатын X кездейсоқ шамасының мәні
медиана деп аталады.
Симметриялық модальдық үлестіру жағдайында (мысалы, бірқалыпты
заң) мода және медиана беттеседі.
* Гюйгенс «Құмар ойындардағы есептесу жөнінде» мемуарларында (1657)
«математикалық күтім» түсінігін және терминін енгізді. МК қазіргі терминін Лаплас
енгізді (1795).
Кездейсоқ шаманың дисперсиясы
X кездейсоқ шамасының оның математикалық күтіміне қарағандағы
шашырауының сипаттамасы дисперсия* болады.
X кездейсоқ шамасының дисперсиясы деп оның математикалық
күтімінен X ауытқуының квадратының ¿орталықтандырылған кездейсоқ
шамасының квадраты) математикалық күтімі аталады, D[ X ] немесе d x , Dx
арқылы белгіленеді:
2
2
D [ X ] =M [ ( X −mx ) ]=M [ Ẋ ] .(4.3 .6)
Дискретті және үзіліссіз кездейсоқ шамалардың дисперсиялары есептеу
үшін сәйкесінше,
n
2
D [ X ] =∑ ( x i−mx ) p(x i ),(4.3 .7)
i=1
∞
2
D [ X ] = ∫ ( x i−mx ) p ( x i ) dx ( 4.3.8)
−∞
формулалары қолданылады.
82.
Дисперсияның анықтамасынан, оның өлшемі X кездейcоқ шамасыныңквадратының өлшемі екендігі көрінеді, ал бұл сан осінде X кездейсоқ
шамасының шашырауын көрсетуге ыңғайсыздық келтіреді. Сондықтан
практикада осындай мағынада үлкен көрнекі болуы үшін σ (x) немесе σ x деп
белгіленетін және дисперсияның квадрат түбіріне тең болатын
σ [ X ]= √ D [ X ] ( 4.3.9)
шашыраудың сипаттамасы – орташа квадраттық
қолданылады.
ОКА және КШ өлшемдері сәйкестенеді.
ауытқу
(ОКА)
4.3.3-мысал. Үлестіру заңы 4.3.1-мысалында келтірілген X кездейсоқ шамасының
дисперсиясын және ОКА табамыз. (4.3.7) формуласымен аламыз:
D [ X ] =( 1−2,50 )2 ∙ 0,20+ ( 2−2,50 )2 ∙ 0,30+¿
+(3−2,50)2 ∙0,30+(4−2,50)2 ∙0,20=1,05.
(4.3.9) формуласымен ОКА анықтаймыз:
σ [ X ]= √ 1,05=1,02.
* «Дисперсия» термині «dispergo» – шашырау, шашылу латын сөзінен шығады.
Түсінікті алғаш рет неміс математигі Лексис енгізді.
Кездейсоқ шаманың моменттері
Кездейсоқ шаманың математикалық күтімінен және дисперсиясынан
басқа ықтималдықтар теориясында кездейсоқ шамалардың кейбір
қасиеттерін көрсету үшін моменттік сипаттамалар немесе моменттер
қолданылады.
X кездейсоқ шамасының k -ші дәрежелі МК X кездейсоқ шамасының k ретті бас моменті деп аталады:
k
α k [ X ] =M [ X ] .( 4.3 .10)
Дискретті және үзіліссіз кездейсоқ шамалардың бас моменттері
сәйкесінше,
n
k
α k [ X ] =∑ x i p ( x i ) ,( 4.3.11)
i=1
∞
α k [ X ] =∫ x k f ( x ) dx (4.3 .12)
−∞
түрінде жазылады.
83.
кездейсоқ шамасының математикалық күтімі X кездейсоқшамасының бірінші ретті моменті екендігіне қарапайым көз жеткіземіз:
α 1 [ X ] =M [ X ] .(4.3 .13)
Төменде қолданылатын екінші ретті бас моментті белгілейміз:
2
α 2 [ X ] =M [ X ] .(4.3.14)
Орталықтандырылған X кездейсоқ шамасының k дәрежесінің
математикалық күтімі X кездейсоқ шамасының k -ретті орталық моменті
деп аталады:
k
μk [ X ] =M [ Ẋ ] , Ẋ= X−mx .(4.3 .15)
Дискретті және үзіліссіз КШ орталық моменттерін есептеу үшін
сәйкесінше,
X
n
k
μk [ X ] =∑ ( x i−mx ) p ( x i ) ,(4.3.16)
i=1
∞
k
μk [ X ] = ∫ ( x−m x ) f ( x ) dx (4.3 .17)
−∞
формулалары қолданылады.
Бірінші орталық момент нөлге тең:
∞
∞
∞
μ1 [ X ] =∫ ( x−mx ) f ( x ) dx=∫ xf ( x ) dx−m x ∫ f ( x ) dx =¿
−∞
−∞
−∞
¿ m x −m x =0.(4.3 .18)
Екінші орталық момент X кездейсоқ шамасының дисперсиясына
(4.3.6) тең:
2
μ2 [ X ] =M [ Ẋ ]=D [ X ] .( 4.3 .19)
Алдағы уақытта X кездейсоқ шамасының үшінші және төртінші мына
түрдегі моменттерін қолданамыз:
3
4
μ3 [ X ] =M [ Ẋ ] , μ 4 [ X ] =M [ Ẋ ] . (4.3 .20)
X кездейсоқ шамасының бас және орталық моменттерінің арасында
байланыс табылады. Мысалы, үзіліссіз X кездейсоқ шамасы үшін әртүрлі
ретті бас және орталық моменттердің байланыстар формулаларын аламыз
(дискреттік кездейсоқ шама үшін де осындай тұжырым жасауға болады).
Екінші орталық моментті (КШ дисперсиясын) қарастырамыз:
∞
2
2
μ2=M [ Ẋ ] =D [ X ] = ∫ ( x−mx ) f ( x ) dx=¿
−∞
∞
∞
2
∞
2
x
¿ ∫ x f ( x ) dx−2 m x ∫ x f ( x ) dx ++m ∫ f ( x ) dx =¿
−∞
−∞
−∞
2
2
2
¿ α 2 [ X ] −2m x + m x =α 2 [ X ]−2m x .(4.3.21)
Үшінші орталық момент үшін ұқсас әрекетпен аламыз:
84.
∞3
3
μ3 [ X ] =M [ Ẋ ]= ∫ ( x−m x ) f ( x ) dx=¿
−∞
∞
∞
∞
3
2
2
x
¿ ∫ x f ( x ) dx−3 mx ∫ x f ( x ) dx +3 m ∫ x f ( x ) dx−¿
−∞
−∞
−∞
∞
3
x
3
−m ∫ f ( x ) dx =α 3 [ X ] −3 m x α 2 [ X ] +2 m x .(4.3 .22)
−∞
Реттері үштен үлкен (>3) орталық моменттер үшін өрнектерді жоғарыдағы сияқты алуға болады. Ақырында формулалар мәліметін аламыз:
μ 1=0 ,
2
μ2=α 2−mx ,
2
μ 3=α 3−3 m x α x +2 mx
………………………
}
.( 4.3.23)
Дисперсияны есептеу үшін екінші және бірінші бас моменттер арқылы
екінші орталық моментті өрнектейтін формула жиі қолданылады:
2
D [ X ] =α 2 [ X ] −mx ,(4.3 .24)
осы формула дискреттік және кездейсоқ шамалар үшін
n
2
2
D [ X ] =∑ x i p ( x i )−mx ,(4.3 .25)
i=1
∞
2
2
D [ X ] = ∫ x f ( x ) dx−m x ( 4.3 .26)
−∞
түрлерін қабылдайды.
Кездейсоқ шаманың үлестіру қисығының ассиметриясын жазу үшін
μ3 [ X ]
Sk= 3
(4.3 .27)
σ [X]
формуласымен есептелетін үшінші орталық момент қолданылады.
4.3.5-мысал. Үлестіру қисықтарының ассиметриялары
Үлестіру қисықтарының екі ассиметриялары 4.3.5-суретте келтірілген.
85.
Эксцесспенсипатталатын
төртінші
орталық
момент
үлестіру
қисықтарының қисықтығын (сүйір немесе жазықтөбелік) жазу үшін
қолданылады. Эксцесс мына формуламен есептеледі:
Ex=
μ4 [ X ]
4
σ [X]
−3.(4.3 .28)
Практикада өте кең қолданылатын үлестірудің нормаль заңы үшін
μ4 [X ]
4
σ [X]
шамасы үшке тең, яғни
μ4 [X ]
4
σ [X]
=3. Сондықтан үлестірудің нормаль
қисығы үшін Ex=0.Үлестірулердің қалған қисықтары нормаль қисықпен
салыстырылады (4.3.6- сурет).
4.3.6-сурет. Үлестіру қисықтарының эксцессі (қисықтығы)
Математикалық статистиканың әртүрлі әдістерін қолданғанда, әсіресе,
белгісіз параметрлердің интервалдық бағалауларын құрғанда әртүрлі
статистиканың критерийлерінде және әдістерінде, F ( x)үлестіру функциясының x q-дің q -квантильдері және 100 q-пайыздық ω qнүктелері түсініктері жиі
қолданылады.
4.3.7-сурет. q деңгейінің квантилі
F ( x ) үлестіру функциясымен берілген үзіліссіз X кездейсоқ шамасының
q деңгейлі квантилі (немесе q-квантилі) деп осы кездейсоқ шаманың x q мәнін
айтады, (X < x q ) оқиғасының ықтималдығы q шамасына тең болса (4.3.7-
сурет):
F ( x q ) =P ( X < x q ) =q .( 4.3.29)
86.
Квантильдің дербес жағдайы – 0,5-квантиль – кездейсоқ шама шашырауларының центрінің сипаттамасы – Me медианасы болады.X дискретті кездейсоқ шамасы үшін x аргументтері өсуімен F (x)
үлестіру функциясының секірмелері өзгереді, демек, (4.3.29) теңдеуін дәл
қанағаттандыратын әрқайсысы x q мүмкін мәндері болмауы мүмкін q
деңгейінің мәндері табылады. Сондықтан q-квантилі F ( x i ( q) ) < q, бірақ
F ( x i ( q)+1 ) ≤ q теңсіздіктерін қанағаттандыратын x i (q ) және x i (q )+1 көршілес екі
мүмкін мәндерінің арасында жататын x i (q ) саны болып анықталады (4.3.8сурет).
4.3.8-сурет. Дискретті кездейсоқ шаманың q квантилі.
q -квантиль q=0,25 ;0,50 ;… ; 0,75 төрттен бірге еселік бекітілген
мәндерінде q деңгейлі квартиль деп аталады. x0,5 квартилі медиана (Ме)
болып табылады.
Бірдің ондық үлесіне еселік q=0,10 ; 0,20 ; … ; 0,90 бекітілген мәндерінде q квантиль q деңгейлі дециль деп аталады.
Бірдің жүздік үлесіне (пайызға) еселік q=0,01 ;0,02 ;… ; 0,99 бекітілген
мәндерінде q -квантиль q деңгейлі процентиль деп аталады.
4.3.9-сурет. Интерквантильді айырма
Түсу ықтималдығы p-ға тең мына кесінді (4.3.9-сурет):
J p=x q −x q , (4.3 .30)
2
1
интерквантильді айырма деп аталады. Басқаша айтқанда, ( p 100 ) %=¿
¿ ( q 2−q 1 ) 100 % барлық нүктелері тиісті кесінді – X кездейсоқ шамасының
87.
мәндері. X кездейсоқ шамасының x q шеткі мәндері J p кесіндісіне тиісті емес,1,2
1
ал көрсетілген кесіндінің әрбір жағынан 2 (1−p)100 пайыздық нүктелер тиісті
(4.3.10- сурет).
4.3.10-сурет. Интерквантильді айырма
4.3.11-сурет. Интерквантильді айырма
Сан осінде J p кесіндісінің центрінің орны математикалық күтімнің
шамасы жөнінде, ал оның өлшемі – шашыраудың (дисперсияның, орташа
квадраттық ауытқудың) шамасы жөнінде түсінік береді.
X кездейсоқ шамасының барлық мәндерінің 50%-ы тиісті мына кесінді
J 0,5
J 0,5 =x 0,75−x 0,25 (4.3 .31)
интерквантильді айырма кесінді деп аталады, сонымен бірге J 0,5
кесіндінің әрбір жағына осы кездейсоқ шаманың барлық мәндерінің 25%-ы
тиісті. Интерквантильді айырманың иллюстрациясы 4.3.11-суретінде берілген.
X кездейсоқ шамасының барлық мәндерінің 80%-ы тиісті мына кесінді
J 0,8
J 0,8 =x 0,9−x 0,1 (4.3.32)
интерквантильдік айырма кесінді деп аталады, сонымен бірге J 0,8
кесіндінің әрбір жағына осы кездейсоқ шаманың барлық мәндерінің 10%-ы
тиісті. Интерквантильді айырманың иллюстрациясы 4.3.12-суретте берілген.
4.3.12-сурет. Интердецильді айырма
Математикалық статистикада квантиль түсінігінің орнына онымен
тығыз байланысты пайыздық нүкте түсінігін қолданады.
88.
X кездейсоқ шамасының 100% (пайыздық) нүктесі деп оның сондай ωмәні түсіндіріледі, X > ωq оқиғасы үшін ықтималдылығы q -ге тең:
1−F ( ωq )=P ( X ≥ ωq )=q . (4.3 .33)
Дискретті кездейсоқ шамалар үшін осы анықтама квантильдің
анықтамасын бергендей түзетіледі.
4.3.13-сурет. q-квантиль, 100%-қ нүкте
(4.3.29) квантильдердің және (4.3.33) пайыздық нүктелердің анықтамаларынан олардың өзара қатынасы шығады (4.3.13-сурет):
x q=ω1−q .(4.3 .34)
5-ТАРАУ
Кездейсоқ шамалар үлестірулерінің негізгі заңдары
5.1. Биномиалдық үлестіру
Бірдей шарттарда өткізілетін n тәуелсіз оқиғалардағы (Бернулли
сынаулары) A оқиғасының пайда болуының саны – биномиалдық заң
бойынша үлестірілген X кездейсоқ шама. X кездейсоқ шамасы Бернулли
(3.7.1) формуласы бойынша анықталатын ықтималдықтармен:
m
m
n −m
P ( X=m) =Pm ,n =Cn p q ,(5.1 .1)
q=1− p , m=0 , … , n
бүтін санды мәндерді {0,1,2, … , m ,… , n } қабылдайды.
Биномиалдық үлестіру екі параметрлерден: p және q -ден тәуелді. X КШ
үлестіру заңы 10-кестеде келтірілген.
10-кесте
x m=m
0
p ( x m )=¿ Pm, n
qn
1
2
npq
n−1
...
n(n−1 ) 2 n−2 ...
pq
2
m
...
k
m m n−m
Cn p q
...
pn
89.
5.1.1-сурет. Биномиалдық үлестірудің көпбұрыштарыүшін p-нің әр түрлі мәндерінде үлестіру көпбұрыштары
5.1.1-суретте көрсетілген. Pm , n ықтималдығының максимумы
n=10
np−q ≤ m≤ np+ p (5.1.2)
шартын қанағаттандыратын m-нің мәндерінде болады. Осы мән m-нің ең
ықтималдық мәні деп аталады.
X кездейсоқ шамасын жылдам есептеулер үшін Pm , n ықтималдықтарының және F n (m) үлестіру функциясының кестесі құрылған:
{
F n ( m )= m−1
0 , m≤ 0 болса ,
∑ Pk , n ,m>0 болса .
(5.1 .3)
k=0
Бірдей шарттарда өткізілетін, n тәуелсіз оқиғаларда A оқиғасының
пайда болу санының математикалық күтімі тең:
M [ X ] =np ;(5.1 .4)
осы санының дисперсиясы тең:
D [ X ] =np ( 1−p )=npq ; (5.1.5)
орташа квадраттық ауытқу тең:
σ [ X ]= √ npq .(5.1.6)
МК, дисперсияның және ОКА қорытып шығару формулалары
5.2-пунктінде беріледі.
Биномиалдық заң бойынша үлестірілген кездейсоқ шамалардың мысалдары
1. n монеталарды үстелдің бетіне лақтырғанда түсетін гербтердің (цифрлардың) саны.
2. Бірдей шарттарды n тәуелсіз атыстарда нысанаға тигізудің саны.
3. Бірдей шарттарда t уақыт ішінде сынауға ұшырайтын n құрылымдардан тұратын
техникалық құрылымның тоқтау саны.
5.1.1-мысал. Бес бірдей типті техникалық құрылымдарға жөндеу өткізіледі. Белгіленген мерзімге жөндеудің орындалуының ықтималдылығы p=0,70 . X кездейсоқ
шамасының – белгіленген мерзімге жөнделген техникалық құрылымдардың санының
үлестіру заңын, математикалық күтімді, дисперсияны, орташа квадраттық ауытқуды және
белгіленген мерзімге үш құрылымнан кем емес техникалық құрылымдардың жөнделгендігінің ықтималдылығын анықтау керек.
Шешуі. (5.1.1) формуласымен n=5 , p=0,70 , q=0,30 болғанда Pm , 5=P ( X=m ) ,
m=0 …5
ықтималдықтарды табамыз:
5
P0,5 =q =0,305=0,002 ,
1
4
4
P1,5=C5 p q =5 ∙0,70 , ∙ 0,30 =0,028,
2 2 3
2
3
P2,5 =C5 p q =10 ∙ 0,70 ∙ 0,30 =0,133,
90.
P3,5=C35 p 3 q 2=10 ∙ 0,703 ∙ 0,302=0,309,4 4
4
P4,5 =C5 p q=5 ∙ 0,70 ∙ 0,30=0,360,
5
5
P5,5= p =0,70 =0,168.
Тексеру:
5
∑ Pm ,5=0,002+0,028+ 0,133+0,309+0,360+0,168=1,000.
m=0
X кездейсоқ шамасының үлестіру қатары мына түрде:
m
0
1
2
3
4
5
Pm,5
0,002
0,028
0,133
0,309
0,360
0,168
mx =np=5 ∙ 0,70=3,500 ,
D x =npq=5∙ 0,70 ∙ 0,3 0=1,050 ,
σ x =√ D x =1,025.
5
P ( X ≥3 )=R3,5 =∑ Pk ,5 =0,309+0,360+0,168=0,837.
k=3
5.2. Туындатқыш функция
Дискретті кездейсоқ шамалардың сандық сипаттамаларын анықтау
үшін туындатқыш функцияның аппаратын қолданады. X кездейсоқ шамасының туындатқыш функциясы деп, Z тәуелсіз (көмекші) айнымалысының
функциясын:
∞
m
φ x ( z ) =∑ z p ( x m ) ( 5.2.1 )
m=0
p ( x m )=P ( X =m )- X кездейсоқ шамасы m (m=0,1,2,…)
айтады, мұндағы,
мәндерін қабылдауының ықтималдығы.
X кездейсоқ шамасының сандық сипаттамаларын (математикалық
күтім, дисперсия) анықтау үшін (5.2.1) туындатқыш функцияның келесі
қасиеттерін қолданады:
1 ¿ φ x ( 1 )=1 ;(5.2 .2)
2 ¿ φ'x ( 1 )=M [ X ] ;(5.2.3)
''
'
'
2
3 ¿ φ x ( 1 ) + φx ( 1 )−[ φ x ( 1 ) ] =D [ X ] .(5.2 .4)
Бірінші қасиет (5.2.1) анықтамасынан шығады және анықталған мағынада нормалдану шарты болады:
91.
∞{
φ x (1 )= ∑ z m p(x m )
m=0
∞
}
z=1
= ∑ p ( xm ) =1.
m=0
Екінші қасиет X дискретті кездейсоқ шамасының анықтамасына (4.3.1)
негізделеді:
∞
{
'
x
φ ( 1 )= ∑ m z
m−1
m=0
∞
p (x m)
} ∑ ( ) []
z =1
=
m=0
mp x m =α 1 X =M [ X ]
.
X кездейсоқ шамасының дисперсиясын бірінші және екінші бастапқы
моменттер арқылы өрнектеуді (4.3.21) қолданып, үшінші қасиетті дәлелдейміз:
2
D [ X ] =α 2 [ X ] −{α 1 [ X ] } =α 2 [ X ] −m2x .
Екінші ретті φ ''x (1 ) туындысын есептейміз:
{
''
∞
φ x (1 )= ∑ m ( m−1 ) z
m−2
m=0
∞
p ( xm)
}
z=1
∞
= ∑ m ( m−1 ) p ( x m ) =¿ ¿
m=0
∞
2
¿ ∑ m p ( x m ) − ∑ mp ( x m )=¿ α 2 [ X ] −α 1 [ X ] . ¿
m=0
m=0
Мынаны аламыз:
''
φ x (1 )=α 2 [ X ]−α 1 [ X ] =α 2 [ X ] −M [ X ] .(5.2 .5)
(5.2.4) формуласына (5.2.3) және (5.2.5) туындыларын қоямыз:
2
2
φ ''x (1 )+ φ'x ( 1 )−[ φ'x ( 1 ) ] =α 2 [ X ] −M [ X ] + M [ X ] −{ M [ X ] } =¿
2
=α 2 [ X ] −{ M [ X ] } =D [ X ].
5.2.1-мысал. Биномиалдық заңмен үлестірілген (5.1-п.) X кездейсоқ шамасының математикалық күтімін және дисперсиясын (5.2.1) туындатқыш функцияның көмегімен анықтаймыз.
Шешуі. (5.1.1) түрінде биномиалдық үлестіруі болатын, X кездейсоқ шамасының туындатқыш функциясы (2.5.6) түрінде болады:
n
n
φ x ( z ) =∑ z P m ,n= ∑ Cnm ¿
m=0
m
m=0
Бірінші қасиетті (5.2.2) (нормалдану шарты) ескереміз:
¿¿
(5.2.6) функциясының туындыларын есептейміз:
φ 'x ( z ) =np( q+ pz)n−1 , φ'x' ( z )=n ( n−1 ) p2 ( q+ pz )n−2 .
92.
Z=1 туындылар келесі түрде болады:'
n−1
=np ,
(5.2 .7)
''
2
2 2
2
φ x (1 )=n ( n−1 ) p =n p −n p .
(5.2 .8)
φ x (1 )=mx =np(q+ p)
X кездейсоқ шамасының дисперсиясын анықтау үшін (5.2.7) және (5.2.8) мәндерін
(5.2.4)-ке қоямыз:
D [ X ] =n2 p2 +n p 2+ np−n2 p2=np ( 1− p )=npq
(5.2 .9)
Сонымен, биномиалдық заңмен үлестірілген кездейсоқ шаманың
математикалық күтімі және дисперсиясы үшін келесі өрнектерді (5.2.7),
(5.2.9) аламыз:
mx =np, D x =npq,
бұлар 5.1-пунктінде (5.1.4), (5.1.5) формулаларымен қорытып шығарылмай
келтірілген. Туындатқыш функция кездейсоқ шаманың үлестіруін бір мәнді
анықтайды және осы тұрғыда қолданылады.
5.3. Пуассон үлестіруі
X кездейсоқ шамасының Пуассон* үлестіруі болады, егер ол бүтін
санды мәндерді (0,1,2,…,m)
m
pm=
a −a (
e 5.3 .1 )
m!
ықтималдықтармен қабылдаса, мұндағыa−¿ үлестіру параметрі, m=0,1,….
5.3.1-сурет. Пуассон үлестіруінің көпбұрыштары
93.
Пуассон үлестіруінің (5.3.1) a параметрі осы заң бойынша үлестірілген X кездейсоқ шамасының бірмезгілде математикалық күтімі және дисперсиясы болатынын төменде көрсетеміз және бұл үлестіру бір ғана a параметрінен тәуелді.X кездейсоқ шамасының үлестіру заңы (үлестіру қатары) 11-кестеде
келтірілген.
*Пуассон Симеон Дени (1781-1840). Француз математигі, механик, физик, Париж
университетінің профессоры. Ықтималдықтар теориясында Пуассон теоремасын – үлкен
сандар заңының дербес жағдайын және шектік теоремалардың бірін тұжырымдады.
Ықтималдықтар теориясындағы маңызды КШ үлестірудің бірі – Пуассон үлестіруін
ұсынды. Петербург ҒА-ның құрметті мүшесі (1826 ж).
11-кесте
x m=m
0
1
p(x m )=Pm
−a
−a
e
ae
2
a2 −a
e
2
…
m
…
…
am −a
e
m!
…
a параметрінің әр түрлі мәндері үшін биномиалдық үлестіру көпбұрыштары 5.3.1-суретте көрсетілген. m-нің ең үлкен ықтималдылық мәні:
a−1 ≤m ≤ a(5.3 .2)
шартынан анықталады.
Егер a−¿бүтін сан болса, онда m-нің m=a−1 және m=a екі мәндерінде
ықтималдық Pm максимум болады;
егер a< 1 болса, онда m=0 -де ықтималдық Pm максимум болады;
егер a бүтін сан болмаса (a> 1), онда m=[ a ] – a бүтін бөлігінде
ықтималдық Pm максимум болады.
Пуассон заңы бойынша үлестірілген кездейсоқ шамалардың мысалдары
1. t уақыт ішінде радиоактивті заттың ыдырауларының саны.
2. t уақыт ішінде ауданы S-ке тең бетке түсетін элементар ғарыштық бөліктердің
саны.
t
3. уақыт ішінде телефон станциясында сөйлесулерге тапсырыстар саны.
Пуассон заңы бойынша үлестірілген кездейсоқ шаманың математикалық күтімін және дисперсиясын анықтау үшін оның (5.2.1) туындатқыш
функциясын табамыз:
94.
∞∞
m
a −a m −a
φ x ( z ) =∑
e z =e ∑ ¿ ¿ ¿
m=0 m!
m=0
Алынған өрнектегі қосынды exp{ az } экспонентаның қатарға жіктелуі,
сондықтан туындатқыш функция тең:
−a az
φ x ( z ) =e e =e
a( z−1)
.
Сонда Пуассон үлестіру үшін туындатқыш функциясы:
φ x ( z ) =e
a(z −1 )
(5.3.3)
болып жазылады.
Оның бірінші және екінші туындыларын табамыз:
φ x ( z ) =ae
'
a(z −1 )
''
a(z −1)
2
φ x ( z ) =a e
,
.
Әрі қарай, (5.2.2)-(5.2.4) туындатқыш функциясы қасиеттеріне сәйкес,
аламыз:
φ x (1 )=e a(1−1)=1 (нормалдану шарты),
'
M [ X ] =φ x ( 1 ) =ae
''
'
a(1−1)
=a ,
'
2
2
2
D [ X ] =φ x ( 1 )+ φ x ( 1 )− {φ x ( 1 ) } =a +a−a =a .
Сонымен, аламыз:
m x = D x =a ,(5.3 .4)
σ x =√ D x =√ a .(5.3 .5)
Пуассон үлестіруін
(5.1.1) биномдық үлестіруі үшінn → ∞, p →0
үмтылғанда шек секілді қарастыруға болады,бірақ көбейтіндіnp=const :
→
n→∞
Pm , n
Pm .(5.3.6)
p→ 0
np=const =a
Осы негізде Пуассон үлестіруін басқаша сирек құбылыстар заңы деп
те атайды ( p →0 ).
(5.3.6) тағайындауының дұрыстығын дәлелдейміз, ол үшін n , p параметрлерімен биномдық заң бойынша үлестірілген математикалық күтімі:
95.
M [ X ] =np=a ,ал әрбір тәжірибедегі А оқиғасының пайда болу ықтималдығы
p=
a
n
мәндеріне тең X кездейсоқ шамасын қарастырамыз.
Бірдей шарттардағы B( X =m) оқиғасының n тәуелсіз тәжірибелерде
пайда болуының ықтималдығын (5.1.1) формуласымен анықтаймыз:
m
Pm , n=P ( B )=Pn ( X=m )=Cn
a m
a n−m
1−
.(5.3 .7)
n
n
( )( )
Осы өрнекті n → ∞ болса шекке көшу ыңғайлы болу үшін мынаған
түрлендіреміз:
n
a
(1− )
n ( n−1 ) … (n−m+1) a
n
lim Pn ( X=m )= lim
∙
∙
m
m!
n→∞
n→ ∞
n
a m
(1− )
n
m
Бірінші бөлшек және соңғы бөлшектің бөлімі n → ∞ болса және ақырлы
m-де бірге тең екендігі қарапайым белгілі. Соңғы бөлшектің алымының шегін
exp{−a } мәніне тең болатындай түрлендіруге болады:
a −n
lim (1− ) a
n
n→∞
[
−a
]
−a
=e .
Демек, (5.3.7) өрнегінің n → ∞ болғандағы шегі тең:
lim Pm , n=
n→∞
a m −a
e =Pm .(5.3 .8)
m!
(5.3.8) нәтижесінде (5.3.6) тағайындауының дұрыстығы расталды –
Пуассон үлестіруі биномдық үлестіру үшін шектік болады. Есептеулердің
ықшамдалуы тұрғысынан биномдық үлестірудің пуассондық жуықтауы
дұрыстығы жөніндегі мысалды қарастырамыз.
5.3.1-мысал. Аппаратураның құрамында n=5000 элементтер бар. Элементтер бір-бірінен
тәуелсіз p=0,001 ықтималдықпен істен шығады. Ең болмағанда, бір элемент тоқтаса, аппаратура
істен шығады. Аппаратураның істен шығуының ықтималдығы қандай?
Шешуі. Істен шыққан элементтердің саны – X кездейсоқ шамасы. Осы шама n=¿ 5000,
p=0,01 параметрлерімен биномдық заң бойынша үлестірілген. Аппаратураның істен шығуын А
деп белгілейміз. А оқиғасы орындалады, ең болмағанда, бір элемент істен шықса,
P ( A )=R1 , 5000 .
96.
Элементтер саны n үлкен және ықтималдық pаз болғандықтан, Пуассон үлестіруінеa=np=¿5000∙0,001=5 параметрімен көшеміз. X =mықтималдығы (5.3.8) формуласымен
анықталады. Ізделінді ықтималдық қарама-қарсы оқиғаның ықтималдығы-на тең:
P ( A )=1−P( A )=1−P ( X =0 ) =1−e−a =1−e−5=1−0,0067=0,9933 .
5.4. Пуассондық ағын және нүктелердің өрісі
Пуассон үлестіруімен байланысқан практикалық есептердің көп саны
оқиғалар ағынымен байланысты тұжырымдалады. Уақыт ішіндегі оқиғалардың тізбегі оқиғалардың (нүктелердің) ағыны деп аталады (5.4.1-сурет).
Оқиғалардың (нүктелердің) пуассондық ағыны екі негізгі қасиеттермен сипатталады:
1. Ағынның жалғыздығы былай түсіндіріледі, оқиғалар (нүктелер) (0 , t )
уақытында осьте біреуден пайда болады, екеуден емес, үшеуден емес және
т.б. (5.4.2- сурет).
Ағынның жалғыздығы қасиетінің ықтималдық сипаттамасы былай
түсіндіріледі, ∆ t уақытында аз интервалға бір нүктеден (оқиғадан) көп
түсуінің ықтималдығы нөлге жақын:
P ( X ( ∆ t ) >1 )=0 , (5.4 .1)
мұндағы, X ( ∆ t ) – ∆ t интервалына түскен нүктелердің саны.
5.4.1-сурет. Нүктелер (оқиғалар) ағыны
5.4.2-сурет. Нүктелердің (оқиғалардың) ағынының жалғыздығы
97.
5.4.3-сурет. Нүктелердің ағынында кейінгі әрекеттерінің болмауы2. Кейінгі әрекеттердің болмауы былай түсіндіріледі, оқиғалар
(нүктелер) (0 , t ) уақытында осьте бір-бірінен тәуелсіз пайда болады.
Кейінгі әрекеттердің болмау қасиетінің ықтималдық сипаттамасы
келесі түрде түсіндіріледі (5.4.3-сурет). Ұзындықтары τ 1 , τ 2 қиылыспайтын
бөліктерде пайда болған нүктелердің (оқиғалардың) санын X ( τ 1) , X (τ 2 ) деп
белгілейміз. Сонда сан өсінде тәуелсіз пайда болған нүктелердің ағыны үшін
мына қатынас дұрыс:
P( X (τ 2 )∨X ( τ 1))=P ¿
мұнда, сол жағы – А оқиғасының шартты ықтималдығы (τ 1 интервалында
X ( τ 1) нүктелері пайда болғанда (В оқиғасы), τ 2 интервалында X (τ 2 ) нүктелері
пайда болады), ал оң жағы – А оқиғасының шартсыз ықтималдығы ¿
интервалында X ( τ 2 ) нүктелерінің пайда болды), яғни шартты ықтимал-дық
шартсыз ықтималдыққа тең, демек, А және В оқиғалары тәуелсіз (1.5.1).
3. Егер ағынның үшінші қасиеті – стационарлық ( λ=const−¿ағынның
интенсивтілігі тұрақты) бар болса, ондай ағын нүктелердің (оқиғалардың)
жай ағыны деп аталады. Осы жағдайда жай ағынның параметрі келесі түрде
анықталады:
a=λτ ,(5.4 .3)
мұндағы, τ – жай ағыны нүктелерінің кездейсоқ саны қарастырылатын
ағымдағы уақыт.
Стационар емес пуассондық ағынның( λ=λ ( t ) ) параметрі:
τ
a=∫ λ(t) dt(5.4 .4 )
0
өрнегімен анықталады.
Бұдан басқа, ұзындығы τ интервалда пуассондық ағынның X (τ ) нүктелерінің (оқиғаларының) саны – Пуассон заңы бойынша үлестірілген
кездейсоқ шама екендігін көрсетеміз.
Осы тұжырымды дәләлдеу үшін ұзындығы τ интервалында λ=const (жай
ағын) интенсивтілікпен нүктелердің пуассондық ағынын қарастырамыз.
98.
[ t , t+ τ ] кесіндісін әрқайсысының ұзындығы ∆ t=τ
болатын тең бөліктерге
n
бөлеміз (5.4.4- сурет).
5.4.4-сурет. Ұзындығы τ бөліктегі нүктелер
∆ t элементар бөлікке түскен нүктелердің санының математикалық
күтімінің шамасы λ ∆t -ға тең екендігі қарапайым. Пуассондық ағынның
жалғыздық қасиетіне сәйкес (5.4.1) ∆ t бөлігіне бір нүкте түсуі немесе нүкте
түспеуі мүмкін (5.4.2-сурет), басқаша айтқанда ∆ t бөлігі екі жағдайларда
болуы мүмкін:
«бөлік бос емес» – ∆ t -ға нүкте түсті;
«бөлік бос» – ∆ t -ға бірде-бір нүкте түскен жоқ.
R оқиғасының индикаторын енгіземіз – ∆ t бөлігіне түскен нүктелердің
саны:
R ( ∆ t )=¿
R ( ∆ t )КШ математикалық күтімі p ( ∆ t )ықтималдылыққа тең:
M [ R ( ∆t ) ] =1 ∙ p ( ∆ t ) +0 ∙ ( 1− p ( ∆ t ) )= p ( ∆ t ) .
Басқа жағынан, [ t , t+ ∆ t ]кесіндісіне түсетін нүктелердің санының
математикалық күтімі M [ R ( ∆t ) ] = λ ∙ ∆ t , бұдан шығады:
p ( ∆ t )=λ ∙ ∆ t=
λ∙τ
.(5.4 .5)
n
n элементар∆ t
бөліктерге нүктелердің түсу процесін n тәуелсіз
тәжірибелер (кейінгі әрекеттердің болмауы) секілді қарастырамыз, ∆ t
бөлігінің әрқайсысында p ( ∆ t ) (5.4.5) ықтималдықпен «бос емес» немесе (
1− p ( ∆ t )) ықтималдықпен «бос», секілді қарастырамыз. ∆ t «бос емес»
λ∙τ
бөліктерінің саны – (5.1.1) биномдық заң бойынша үлестірілген nжәне P= n
параметрлерімен кездейсоқ шама болады. ∆ t бөліктерінің X ( τ ) , оларға түскен
нүктелермен «бос еместігінің» санының ықтималдығы m-ге тең, мына түрде
болады:
99.
mλτ n−m
m λτ
(
)
P ( X τ =m )=C n
(1− ) .(5.4 .6)
n
n
( )
Әрі қарай ∆ t бөліктерінің санын шексіз өсіреміз, басқаша айтқанда,
n → ∞, және ұзындығы τ [ t , t+ τ ] кесіндісіне дәл m нүктелердің түсуінің Pm
ықтималдығын шекте анықтаймыз:
Pm= lim C mn
n→ ∞
λ∙τ
n
m
( )
n−m
(1−
λ∙τ
)
n
.(5.4 .7)
Бірақ осыған ұқсас есеп 5.3-пунктінде қарастырылған болатын,
λτ
мұндағыn → ∞ , p ( ∆ t )= n → 0 , биномдық үлестіру шегіндеa=λτ параметрімен
пуассон үлестіруіне ұмтылады:
( λτ)m −λτ
P m=
e =P ( m , λτ ) ,(5.4 .8)
m!
дәлелдеу керегі осы болатын.
5.4.1-мысал. Техникалық құрылымның істен шығуларының ағыны λ=0,10 (1/сағат)
жай интенсивтіліктен болады. τ =3 сағат жұмыс жасағанда ең болмағанда, техникалық
құрылымның біреуінің істен шығуын, ал бұл оның жұмыс жасамауына апарып соғады,
ықтималдығы қандай?
Шешуі. Техникалық құрылымның τ уақыт ішінде жұмыс жасамауларының саны –
a=λτ=0,10∙ 3=0,30 параметрімен Пуассон заңы бойынша үлестірілген кездейсоқ шама.
Техникалық құрылымның жұмыс жасамауының (А оқиғасы) ықтималдығы – ең
болмағанда, біреуінің істен шығуының R1 ықтималдығы мынаған тең:
−a
−0,30
P ( A )=R1 =1−P0=1−e =1−e
=0,26.
5.4.2-мысал. Автоматты телефон станциясына түсетін телефон шалулардың
тапсырыстар ағыны – интенсивтілік λ=10 (1/мин) жай ағын. τ =0,1 минут ішінде АТС-ке
бірден көп тапсырыстар түсуінің ықтималдығы қандай?
Шешуі.τ =0,1 мин ішінде АТС-ке түсетін тапсырыстар саны:
a=λτ=10 ∙ 0,10=1(тапсырыс )
параметрімен Пуассон заңымен үлестірілген кездейсоқ шама.
τ уақыты ішінде бір тапсырыстан көп (ең болмағанда, екеу) түсуінің ықтималдығы
тең:
∞
P ( B )=R2= ∑ P m=1−( P 0+ P 1) =1−( e−a+ ae−a )=1−2 e−1=1−2 ∙0,368=¿ 0,264.
m =2
Интенсивтілігі
100.
λ * = λ ∙ p , 0¿ p<1(5.4 .9)шартынан анықталатын пуассондық ағын сиретілген пуассондық ағын деп
аталады. Объектіге теріс қайта әсер ететін пуассондық ағынды қарастырамыз. Қайта әсер етулердің әрқайсысы P ықтималдықпен төтенше («қатты
әсер ететін») болады. Демек, істен шығару үшін (талқандау, қалыпты жұмыс
жасауды тоқтату және т.б.) ең болмағанда, бір «төтенше» қайта әсер ету
жеткілікті. Пуассондық ағын жалғыздығының (5.4.1) күшіне сәйкес объектінің істен шығуының (В оқиғасы) ықтималдығын сиретілген пуассондық
ағында λ * (5.4.9) интенсивтілікпен теріс қайта әсер етулердің ең болмағанда,
біреуінің объектіге «қатты әсер етуінің» ықтималдығы түрінде түсіндіруге
болады:
¿
P ( B )=1−P¿0 =1−e−a .(5.4 .10)
Мұнда, a ¿= λpτ , τ −¿ объектіге қайта әсер ету уақыты.
5.4.3-мысал. Сейсмикалық белсенділік зонасында салынған объекті жер сілкінгенде p=0,10 ықтималдықпен қирайды. Жер сілкінулерінің ағынын λ=5 интенсивтілікпен
жай пуассондық деп
есептейміз. Бір жылдың ішінде объектінің қирауы-ның
ықтималдығы қандай?
Шешуі. Объект үшін қауіпті («өте қатты әсер ететіні») сиретілген пуассондық
ағынға көшеміз. Ондай ағынның интенсивтілігі:
λ *= λ p=5∙ 0,10=0,50 (қауіпті қатты әсер етулер).
Сиретілген ағынның параметрі a ¿ тең: a ¿= λ¿ τ =0.50 ∙1=0.50. Объектінің істен
шығуының (қирауының) – В оқиғасының ықтималдығын (5.4.10) формуласы бойынша
есептейміз:
¿
P ( B )=1−e−a =1−e−0.50=1−0,606=0,394.
Нүктелердің (оқиғалардың) сандары жөніндегі қорытынды,[ t , t + τ ]
уақыт осінің кесіндісіне түскен, Пуассон заңы бойынша нүктелердің
(оқиғалардың) пуассондық жағдайында нүктелердің жазықтықтағы (нүктелердің кездейсоқ жазық өрісі) және үш өлшемді кеңістіктегі (нүктелердің
кеңістіктегі кездейсоқ өрісі) жағдайларына таратылады.
Нүктелердің кездейсоқ өрісі пуассондық өріс деп аталады, егер
төмендегі шарттар сақталса:
1. Өрістегі нүктелер λ орташа тығыздықпен (1/аудан бірлігі немесе 1/көлем
бірлігі) бірқалыпты статистикалық таратылады.
101.
2. Нүктелер біреуі екіншісінен тәуелсіз болып, қиылыспайтын аумақтарғатүседі (кейін әсер етулердің болмауы).
3. Нүктелер ауданның (көлемнің) аз элементіне бір-бірден (екеуден емес,
үшеуден емес және т.б.) түседі – жалғыздығы.
Осы шарттар сақталғанда G -дің кез келген аумағына (жазықтықтағы
немесе кеңістіктегі) X нүктелерінің саны Пуассон заңы бойынша
үлестіріледі, ал m нүктелердің G аумағына түсуінің ықтималдығы Pm
формуласы(5.3.1) бойынша анықталады:
Pm ( G )=P ( X ( G )=m) =
a m −a
e , m=1,2,3 , … ,(5.4 .12)
m!
мұндағы, a – G аумағына түсетін нүктелердің санының математикалық күтімі.
Жазықтықтағы жағдай үшін:
a=SG ∙ λ ,(5.4 .13)
кеңістіктегі жағдай үшін:
a=V G ∙ λ ,(5.4 .14)
мұндағы, sG , V G- G аумағының сәйкесінше ауданы, көлемі.
5.4.4-мысал. Ұшақ қиыршық тастар шашылған алаңға қонуға мәжбүр болады.
Тастарға соғу төтенше жағдайға алып келеді. Тастар λ s=0,001(1 / м2 ) тығыздықпен
пуассондық өрісті құрайды. Ұшақ шоссесі колеясының ұзындығы l=4м, алаң бойынша
жолдың ұзындығы L=100 м. Ұшақтың сәтті қонуының ықтималдығы қандай?
Шешуі. Ұшақтың «жүгіріс ауданы» S= L∙ l=100 ∙ 4=400 ( м 2). Ұшақтың жолында
болуы
мүмкін
қиыршық
тастардың
орташа
саны
(алаңның
параметрі),
a=λ s ∙ S=0,001∙ 400=0,4 . Сәтті қонудың (А оқиғасы) ықтималдығы алаң бойынша жүріс
кезіндегі ұшақтың жолында бірде-бір тас кездеспеуінің («жүгіріс ауданында»)
ықтималдығына тең:
−a
P ( A )=P0 =e =e
−0.40
=0.67 .
5.4.5-мысал. Ауру тарататын микробтарды – тұмаудың қоздырғыштарын айқындауға ауадан сынама алынды. Микробтардың орташа тығыздығы λ V =100 (1/ м 3). Сынама
үшін 1 дм3 ауа жиналады. Тұмаудың ең болмағанда, бір қоздырғышы табылуы-ның
ықтималдығы қандай?
Шешуі.a=λV ∙ V =100 ∙ 0,001=0,10 параметрімен ауру тарататын микробтар-дың
кеңістіктегі пуассондық өрісімен жұмыс жасаймыз деп ұйғарамыз. 1 дм 3 ауада ең
болмағанда, бір микробтың табылуының ықтималдығы тең:
102.
R1=1−P0=1−e−0,10=0,095 ( 95 % ) .Пуассон заңын қолдануға байланысты жылдам есептеулер үшін:
P ( k , a )=
a k −a
e =P k ,(5.4 .15)
k!
m
R ( m ,a )=∑ P( k , a),(5.4 .16)
k=0
∞
R ( m , a )= ∑ P (k , a)(5.4 .17)
k=m
кестелік функциялар қолданылуы мүмкін.
Пуассондық қосындылар R ( m ,a ) (5.4.16) немесе R ( m , a ) (5.4.17)
қолданумен Pk (5.4.15) ықтималдықтарының анықтамалары бойынша
есептеулерді жылдам жасауға мүмкіндік беретін келесі қатынастар
қарапайым:
R ( m , a )=1−R ( m−1, a ) ,(5.4 .18)
R ( m ,a )=1−R ( m+1 , a ) ,(5.4 .19)
Pk =P ( k , a )=R ( k , a ) −R ( k−1 , a ) ,(5.4 .20)
Pk =P ( k , a )=R ( k , a ) −R ( k +1 , a ) .(5.4 .21)
P ( k , a ) және R ( m , a ) функцияларының кестелері 10-, 11-қосымшаларда
берілген.
5.5. Геометриялық үлестіру
А оқиғасының бірінші пайда болуына дейінгі, бірдей шарттарда
орындалатын¿), екі нәтижелермен (А және А оқиғалары) X тәуелсіз
тәжірибелер сандарының үлестіру заңы геометрия-лық деп аталады.
Х КШ мүмкін мәндері (1, 2, 3, …, m) сандары болады. А оқиғасы mтәжірибеде пайда болатындығының, Bmоқиғасының ықтималдығы, ал
алғашқы (m−1)тәжірибелерде пайда болмағандығының ¿ рет қарама-қарсы A
оқиғасы пайда болды) ықтималдығы тең:
P ( B m )=P ( X =m )=q m−1 ∙ p .(5.5 .1)
103.
Геометриялық заң бойынша үлестірілген X кездейсоқ шамасыныңгеометриялық үлестіруі бірінші мүшесі p және еселігі q (0< q<1)
геометриялық прогрессиямен көрсетіледі (12-кесте). Сондықтан (5.5.1)
үлестіруі геометриялық деп аталған.
12-кесте
x m=m
1
2
3
…
p ( x m )=Pm
p
qp
q p
2
…
M
q
m−1
…
p
…
параметрінің әр түрлі мәндері үшін үлестіру көпбұрыштары
5.5.1-суретте көрсетілген.
p
5.5.1-сурет. Геометриялық үлестірудің көпбұрыштары
Геометриялық үлестірудің мысалдары
1. Бірінші рет пайда болғанға дейін монетаны лақтырудың саны.
2. Ұшу кезінде тоқтаған ұшақтың қозғалтқышын іске қосу әрекеттерінің саны.
3. Бірінші тигізуге дейін нысана бойынша атулардың саны.
(5.2.1) өрнегіне сәйкес геометриялық үлестірудің туындатқыш
функциясы тең:
∞
m
∞
φ x ( z ) =∑ Pm z =pz ∑ ¿ ¿
m=1
m=1
104.
φx (z ) =pz
.(5.5 .2)
1−qz
Х КШ МК және дисперсиясын анықтау үшін φ 'x ( z ) , φ'x' ( z ) туындыларды
табамыз, бірақ алдын ала (5.2.2) туындатқыш функциясының бірінші
қасиетін – нормалдану шартын тексереміз:
φ x (1 )=
p
p
= =1.
1−q p
φ x ( z ) функциясының туындылары келесі өрнектермен анықталады:
φx (z )=
p ( 1−qz ) + qpz
p
=
,(5.5 .3)
2
(1−qz )
(1−qz)2
φ 'x' ( z ) =
2 pq
.(5.5 .4)
(1−qz )3
'
(5.5.3), (5.5.4) туындыларының z=1 болғанда мәні келесілер:
φ 'x (1 )=
''
φ x (1 ) =
p
1
= =mx ,(5.5 .5)
2
(1−q) p
2 pq
2q
= 2 .(5.5 .6)
3
(1−q)
p
Х КШ дисперсиясын (5.2.4) формуласы бойынша есептейміз:
''
'
D x =φ x ( 1 ) +φ x ( 1 )−¿ ¿
Х кездейсоқ шамасының ОКА тең:
q
σ x =√ D x = √ .(5.5 .8)
p
Соңында аламыз:
mx =
1
q
q
, D x= 2 , σ x= √ .
p
p
p
5.5.1-мысал. Баренц теңізіндегі акваторийда қиын жағдайға ұшыраған кемені табу
үшін метеорологиялық төтенше жағдайлар ұшағы жүйелі ұшу жасайды. Бір рет ұшқанда
кемені табу ықтималдығы p=0,40. Х іздестіру ұшуларының санының үлестіру заңын,
олардың МК, дисперсиясын, ОКА және кеменің үшінші ұшуда табылуының
ықтималдылығын анықтау керек.
Шешуі. Кемені табуға дейінгі Х ұшуларының саны – геометриялық заң бойынша
үлестірілген, (5.5.1) өрнегімен анықталатын кездейсоқ шама:
Pm=P ( X =m )=0,60 m−1 ∙ 0,40.
105.
Х КШ үлестіру қатары 13-кестеде келтірілген (5.5.1-суретті қараңыз).13-кесте
Іздестіру ұшуларының санының үлестіру қатары
m
1
2
3
4
5
6
7
…
Pm
0,400
0,240
0,144
0,086
0,052
0,031
0,019
…
mx =
1
=2,5(ұшулардың),
0,4
D x=
0,6
=3,75 , σ x =√3,75=1,94 (ұшулардың),
2
0,4
P3=P ( X =3 )=0,144.
5.6. Көрсеткіштік үлестіру
Ықтималдықтың тығыздығы
−λx
f ( x )= λ e , x ≥ 0 , (5.6.1)
0 , x< 0 ,
{
мұнда, параметр λ – тұрақты оң шама, өрнегімен берілетін X ∈ [ 0 , ∞ ) үзіліссіз
кездейсоқ
шамасы
ықтималдықтарының
үлестіруі
көрсеткіштік
(экспоненциалдық) деп аталады.
Х КШ үлестіру функциясы F ( x) (5.6.1) f (x)
тығыздығымен, (4.2.18) формуласымен байланысқан:
x
x
− λt
F ( x )=∫ f ( t ) dt=λ ∫ e
0
ықтималдықтың
−λx
dt=1−e
.
0
5.6.1-сурет. Экспоненциалдық үлестірудің ықтималдығының тығыздығы
106.
5.6.2-сурет. Экспоненциалдық үлестірудің үлестіру функциясыСоңында аламыз:
F ( x )=
;
(5.6 .2)
{1−e0 , x ≤, x0болса
>0 болса .
−λx
Көрсеткіштік үлестірудің тығыздығы және функциясының графиктері
5.6.1-, 5.6.2-суреттерінде келтірілген.
Үлестіру функциясының геометриялық кескінделуі 5.6.3-суретінде
(4.2.18 формуласы) көрсетілген.
5.6.3-сурет. F ( x) үлестіру функциясының геометриялық мағынасы
Көрсеткіштік заң бойынша үлестірілген Х КШ ¿жартылай интервалына
түсуінің ықтималдығын ¿ аралығындағы үлестіру функциясының өсімшесі
cекілді (5.6.2-сурет) анықтауға болады, (4.2.9) формуласы:
P ( X ∈ [ α , β ) ) =F ( β )−F ( α )=e−λα −e−αβ .(5.6 .3)
Ықтималдық тығыздығының (5.6.1-сурет) графигінде кесіндіге түсудің
ықтималдығы α , β нүктелерінің ординаталарымен шектелген f ( x) қисығының астындағы аудан түрінде өрнектеледі.
Көрсеткіштік үлестіруі болатын Х КШ математикалық күтімі және
дисперсиясы (4.3.3), (4.3.4) формулалары бойынша анықталады:
107.
∞∞
−λx
m x =∫ xf ( x ) dx=λ ∫ x e
0
dx . (5.6.4 )
0
(5.6.4) өрнегін бөліктеп интегралдау арқылы аламыз:
1
mx = ,(5.6 .5)
λ
∞
∞
2
2
x
2 − λx
D x =∫ x f ( x ) dx−m = λ∫ x e
0
0
dx−
1
.(5.6 .6)
2
λ
(5.6.6) өрнегін бөліктеп интегралдап, аламыз:
1
D x = 2 .(5.6 .7)
λ
ОКА дисперсиядан (5.6.7) квадрат түбір тапқанға тең:
1
σ x = .(5.6 .8)
λ
Сонымен МК және ОКА λ үлестіруінің параметріне кері пропорционал,
ал дисперсия λ 2 шамасына кері пропорционал.
5.6.1-мысал. Үзіліссіз Х КШ λ=0,01 параметрімен көрсеткіштік заң бойынша
үлестірілген. Оның үлестіру заңын және сандық сипаттамаларын табу керек.
Шешуі. Х КШ ықтималдық тығыздығы (5.6.1) түрінде болады:
f ( x )=0,01e−0,01 x ,
үлестіру функциясы (5.6.2) түрінде болады:
F ( x )=1−e−0,01 x .
(5.6.5), (5.6.7), (5.6.8) сандық сипаттамалары тең:
mx =100 , D x =10000 , σ x =100.
Көрсеткіштік үлестіру техникалық қолданыстарда кең пайдаланылады, сірә, екі жағдайлардың әсерінен. Біріншіден, көрсеткіштік үлестіру тек
қана бір параметрге тәуелді, бұл оған көп параметрлі үлестірулерге қарағанда
артықшылық береді. Екіншіден, заңның экспонента арқылы өрнектелуі,
жеңіл дифференциалданатын және интегралданатын, кездейсоқ шаманың
моменттері және сипаттамалары үшін жай тәуелділікті алуға мүмкіндік
береді.
Практикалық есептер үшін көрсеткіштік үлестірудің аса маңызды екі
қолданыстарын қарастырамыз:
108.
1) сенімділік теориясында техникалық жүйенің (агрегаттық жүйеэлементінің) тоқтаусыз жұмыс жасау уақытының үлестіру заңы.
2) «массаны» қамтамасыз ету теориясында және оқиғалардың (нүктелердің) ағындарымен байланысты басқа есептерде, екі тізбектелген
оқиғалардың пуассондық ағын арасындағы уақыт интервалындағы
үлестіру заңы сияқты.
Бірінші есеп. Т моменті ішінде техникалық құрылғының бірінші
тоқтауға дейін тоқтаусыз жұмыс жасауының ықтималдығы сенімділік
функциясымен өрнектеледі:
p ( t ) =P ( T ≥t ) ,(5.6 .10)
мұнда, КШТ – тоқтауға жұмыс жасау уақыты.
t=0 болса, сенімділік функциясы бірге тең және техникалық
құрылғының уақытының өсуіне сәйкес нөлге дейін кемиді (5.6.4-сурет).
Техникалық құрылғының t уақыты ішінде тоқтауының ықтималдығы
Т КШ үлестіру функциясына тең:
q ( t )=1−p ( t )=P ( T <t ) =F ( t ) .(5.6 .10)
5.6.4-сурет. Сенімділік функциясы
Т кездейсоқ шамасының үлестіруі көрсеткіштік заң деп ұйғарып,
тоқтап және тоқтаусыз жұмыс жасаудың сәйкесінше ықтималдықтарын
аламыз:
q ( t )=1−e−λt ,(5.6 .11)
p ( t ) =e− λt .(5.6 .12)
109.
5.6.5-сурет. Көрсеткіштік үлестірудің қасиетін дәлелдеуге қолданыладыТоқтауға жұмыс істеудің орташа уақыты (T уақытының математикалық күтімі) тең (5.6.5):
1
M [ T ] = ,(5.6 .13)
λ
бұдан тоқтауға жұмыс жасау Т уақытының үлестіру заңының параметрі
λ:
λ=
1
(5.6 .14)
M [T ]
өрнегімен анықталады және техникалық құрылғы тоқтауларының интенсивтілігі деп аталады.
Көрсеткіштік үлестіру қолданыстар үшін маңызды қасиеттерге ие
болады: ∆ t ұзындықпен интервалдық уақытта техникалық құрылғының
тоқтаусыз жұмыс жасауының ықтималдығы қарастырылатын интервалдың басына дейінгі уақыттан тәуелсіз, ал тек қана ∆ t уақыттық
интервалдан тәуелді (кейінгі әрекеттердің болмауы).
Осы қасиетті дәлелдеу үшін (5.6.5-сурет) белгілейміз:
А – техникалық құрылғының (0,t 0 ¿ интервалында тоқтаусыз жұмыс
істеуі;
В – техникалық құрылғының(t 0 ,t 0 +∆ t ) интервалында тоқтаусыз жұмыс
жасауы;
АВ – техникалық құрылғының (0;t) интервалында тоқтаусыз жұмыс
жасауы.
Осы оқиғалардың ықтималдықтары (5.6.12) формулалары бойынша тең:
−λt 0
P ( A )=e
−λt
P ( AB ) =e
=e
, P ( B )=e− λ∆ t ,
−λ(t 0 +∆ t )
− λt 0
=e
∙e
− λ∆ t
.
110.
P(B|A) шартты ықтималдығы, техникалық құрылғы ∆ t (t 0 ,t 0 +∆ t)интервалында тоқтаусыз жұмыс істейді, егер ол t 0 моментіне дейін тоқтаусыз
жұмыс істесе (1.4.7) формуласымен есептеледі:
P ( B| A )=
P ( AB ) e−λ t e− λ∆ t −λ ∆ t
=
=e
.
−λt
P( A)
e
0
0
5.6.6-сурет. Нүктелердің ағыны
Алынған өрнекте t 0 жоқ, ал тек қана ∆ t бар, бұл мынаны көрсетеді:
(t 0 ,t 0 +∆ t)
(0 , t 0) интервалында техникалық
интервалының алдындағы
құрылғының жұмыс жасау уақыты тек қана осы интервалдың ∆ t
ұзындығынан тәуелді болатын келесі интервалдағы техникалық құрылғының тоқтаусыз жұмыс жасауы ықтималдығының шамасына әсер етпейді,
дәлелдеу керегі осы еді.
Екінші есеп. Жай пуассондық оқиғалардың (нүктелердің) ағынында екі
тізбектелген келесі оқиғалардың арасындағы уақыт интервалының ұзындығы λ параметрімен көрсеткіштік заңға ие (5.6.6-сурет):
f ( t )= λ e−λt ,t >0.
Шынында, айталық t k моментінде Ak оқиғасы пайда болды дейік
(5.6.7-сурет). Одан кейінгі Ak +1 оқиғасы кездейсоқ Т уақыт аралығы арқылы
пайда болады.
Ak +1 оқиғасы пайда болғанға дейінгі Т уақытының үлестіру функциясын
табамыз, ол үшін t уақытының моментін бекітеміз ((t k , t k+1 ¿ интервалы аз).
Келесі Ak +1 оқиғаның осы интервалға түсуінің ықтималдығы Т кездейсоқ
шамасының үлестіру функциясы болады:
P ( T <t )=F ( t ) .
Оқиғалар ағыны жай (пуассондық) болғандықтан, онда (5.4.1)
ағынының жалғыздық қасиетіне сәйкес (t k ,t k+ 1) аз интервалда осы интервалға
Ak +1оқиғасының ықтималдығы түсуі осыған ең болмағанда, бір оқиға түсуінің
ықтималдығына тең:
− λt
P ( T <t )=R 1=1−P0=1−e
,(5.6 .15)
111.
мұнда, λt=a – пуассондық үлестірудің (5.3.1) параметрі – (t k , t k+1 ¿ интервалынатүскен оқиғалар (нүктелер) санының математикалық күтімі.
(5.6.15) өрнегін (5.6.2) өрнегімен салыстырып, жоғарыдағы жасалған
тағайындаудың дұрыс екендігіне көз жеткіземіз.
5.6.7-сурет. Жай нүктелер ағынында көршілес нүктелердің арасындағы уақыт
интервалын үлестіру заңын қорытуға қолданылады
5.6.2-мысал. λ=0,01 ¿ ¿ параметрімен берілген көрсеткіштік заңмен – Т кездейсоқ
шамасы – техникалық құрылғы элементінің тоқтауына жұмыс жасау уақыты үлестірілген.
Тоқтауға жұмыс жасаудың орташа уақытын (математикалық күтімін), t =80 сағатта
элементтің тоқтаусыз жұмыс жасауының ықтималдығын және 100 сағаттан 120 сағатқа
дейінгі тоқтау ықтималдығын анықтау керек.
Шешуі. Оқиғаларды белгілейміз: А – 80 сағат ішінде элементтің тоқтаусыз жұмыс
жасауы, В – (100; 120) сағат интервалында элементтің тоқтауы. Тоқтауға жұмыс
жасаудың уақыты (5.6.13) және ізделінді ықтималдықтар (5.6.3) сәйкесінше тең:
1
1
M [T ]= =
=100 ( са ғ ) ;
λ 0,01
−0,01 ∙ 80
P ( A )=P ( T ≥ 80 ) =1−P ( T <80 )=1−F ( 80 )=1−( 1−e
−0,01 ∙80
¿e
−0,80
=e
) =¿
=0,45 ;
P ( B )=P ( 100<T <120 )=F ( 120 ) −F ( 100 )=e−0,01 ∙ 100−e−0,01∙ 120 =¿
−1
−1,2
¿ e −e
=0,07.
5.6.3-мысал. Техникалық агрегаттарды жөндеуге тапсырыстардың пуассондық
1
ағыны λ=0,10
параметрімен (интенсивтілікпен) сипатталады. Жөндеуге агрегат
c
түскеннен кейін келесі агрегаттың 5 сағат ішінде түсуінің ықтималдығы қандай?
Шешуі. Ізделінді оқиғаны А деп, ал тапсырыстар арасындағы уақытты Т арқылы
белгілейміз. А оқиғасының ықтималдығы тең:
P ( A )=P ( T < 5 )=F ( 5 )=1−e−0,10∙ 5=1−e−0,50=1−0,606=0,394.
Мұнда, F(t) үлестіру функциясы (5.6.2) формуласы бойынша анықталады.
112.
5.7. Бірқалыпты үлестіруa-дан b-ға дейінгі бөлікте Х үзіліссіз кездейсоқ шамасының
бірқалыпты үлестіруі болады (бірқалыпты тығыздық заңы бойынша
үлестірілген), егер оның осы бөліктегі ықтималдық тығыздығы тұрақты
болса (5.7.1-сурет):
f ( x )=
1
, x ∈ [ a ,b ] ,
(5.7 .1)
b−a
0 , x [ a , b ] ( x <a , x> b ) .
{
5.7.1-сурет. Бірқалыпты үлестірудің ықтималдық тығыздығы
5.7.2-сурет. Бірқалыпты үлестірудің үлестіру функциясы
Х КШ бірқалыпты үлестірудің үлестіру функциясы (4.2.18) формуласы
бойынша анықталады және тең (5.7.2-сурет):
0 , x <a ,
x−a
F ( x )=
, a≤ x <b , (5.7 .2)
b−a
1 , x ≥b .
{
(4.2.18) ықтималдықтың тығыздығы мен функцияның байланысын
көрсететін формулаға сәйкес үлестіру функциясының геометриялық интерпретациясы 5.7.3-суретте берілген. Үлестіру функциясы F ( x ) жоғарыдан
113.
үлестіру қисығымен шектелген және x нүктесінің ординатасының солжағында жатқан ауданға тең.
Бірқалыпты үлестірілген Х кездейсоқ шамасының α -ден β-ға дейінгі
бөлікке түсуінің ықтималдығы α-ден β-ға дейінгі ықтималдықтың
тығыздығынан интеграл немесе ¿,β) жартылай интервалында үлестіру
функциясының өсімшесі түрінде анықталады және тең:
P¿
5.7.3-сурет. Үлестіру функциясының интерпретациясы
(5.7.3) формуласының геометриялық интерпретациясы 5.7.1- және
5.7.2-суреттерінде берілген.
Х кездейсоқ шамасының, бірқалыпты үлестірілген сандық сипаттамалары (МК, дисперсия) (4.3.3) және (4.3.4) формулалары бойынша анықталады
және тең:
b
1
a+ b
dx=
,(5.7 .4)
b−a
2
mx =∫ x
a
b
2
D x =∫ x
a
2
1
b+ a 2 ( b−a )
dx−
=
, (5.7 .5)
b−a
2
12
σ x =√ D x =
( )
b−a
.(5.7 .6)
2 √3
Бірқалыпты үлестірілген КШ мысалдары:
1. «Өрескел» шкалалы өлшеу құралымен өлшенгенде жіберілетін қате (өрескел
өлшеулердегі қате). Мысалы, затты сантиметрлік бөліктермен бөлінген сызғышпен
өлшегенде санау үшін шкаланың бүтін жақын саны алынады (5.7.4-суретте 3 см).
1 1
ΔХ КШ өлшеу қатесі [- , ¿ (қараңыз) интервалында бірқалыпты үлестірілген
2 2
болады.
114.
5.7.4-сурет. Өрескел өлшеулердегі қате2. Айналуға келтірілген дөңгелектің (Ox) сызығымен және ОА бекітілген радиусы
арасында жасалған кездейсоқ бұрыш Ф, дөңгелектің айналуын тоқтатқаннан
кейінгі [0 0 , 3600] немесе [0,2π] интервалда бірқалыпты үлестірілген кездейсоқ
шама. Осы тектес диск құмар ойындарда немесе кездейсоқ сандарды
араластырғанда қолданылатын рулетканың моделі. Рулетка (компьютерлік
стандарттық программа RANDOM*), R ∈ [ 0,1 ] кездейсоқ сандарын араластыратын
(қыздыратын, 5.7.6-сурет) [0,1] интервалында бірқалыпты үлестірілген кездейсоқ
сандарды модельдеуде қолданылады.
5.7.5-сурет. Дискіні тоқтатқаннан кейінгі кездейсоқ бұрыш
3. Метрополитен станциясына түскен жолаушының пойызды күту уақыты T [0; ∆ t]
интервалында бірқалыпты заң бойынша үлестірілген кездейсоқ шама, мұнда, ∆ t –
пойыздың қозғалысының интервалы («үдеме» қимыл сағатында ∆ t=2 мин.)
*Random – кездейсоқ (ағылшынша).
5.7.6-сурет. Кездейсоқ сан ықтималдығының тығыздығы
115.
5.7.1-мысал. 1 градус дәлдік (құралдың шкаласының бөлу бағасы) құралымен φбұрышты өлшеу жүргізіледі. Осы құралмен ∆ φ бұрышты өлшеудің қателігі градустың
төрттен бірінен (15' ¿ өспейтіндігінің ықтималдылығы қандай?
Шешуі. ∆ Ф бұрышын өлшеудің қателігі – кездейсоқ шама [−30' , 30' ] интервалында бірқалыпты үлестірілген (5.7.7-сурет). Ізделінді А оқиғасы – ∆ Ф қателігі (± 15' )
шамасынан артпайды. Демек, P ( A ) ықтималдығы – б ұ л ∆ Ф кездейсоқ шамасының
[−15' , 15' ]кесіндісіне түсуінің ықтималдығы. (5.7.3) формуласы бойынша ізделінді
ықтималдық тең:
P ( A )=
15' −(−15' )
=0,50.
'
'
30 −(−30 )
P ( A ) ықтималдығының сан мәні f (∆ φ) үлестіру қисығының астындағы ± 15'
нүктелерінде ординаталарымен сол және оң жағынан шектелген ауданға тең
(5.7.7-суретті қараңыз).
5.7.7-сурет. Бұрыштық өлшеу қателігі үлестіруінің заңы
5.7.2-мысал. Отын құятын ұшақпен (танкер) отынды қажет ететін ұшақтың (мұхит
үстінен ұзақ уақыт ұшқаннан соң), оларды шартты С 1және С 2 деп атаймыз, кездесу
уақыты 12.00-ден 12.02-ге дейінгі уақыт аралығына белгіленген. Отын құюдың берілген
ауданында белгіленген уақытының алғашқы 30 cекундта С 1және С 2 кездесуінің
ықтималдықтары қандай?
Шешуі. Берілген ауданда берілген 12.00 мерзімінің басынан кейін ұшақты күтудің
уақыты – [0;2 мин] интервалында бірқалыпты үлестірілген кездейсоқ шама. Берілген отын
құюдың ауданына бекітілген мерзімнің алғашқы 30 cекундында келудің ықтималдықтары
бірдей p1 ж ә н е p2тең (5.7.3):
p1= p2=P ( T ∈ [ 0 ;0,5 мин ] ) =
0,5−0
=0,25.
2−0
Бекітілген мерзімнен алғашқы 30 секундта берілген ауданда екі ұшақтың
кездесетіндігінің (В оқиғасы) ізделінді оқиғасы (3.1.9) тәуелсіз оқиғалардың
ықтималдықтарын көбейту теоремасымен табылады және мынаған тең:
P ( B )=P1 ∙ P2=¿ ( 0,25) =0 ,0625 ≈0,06.¿
2
116.
5.8. Нормаль үлестіруҮлестірудің нормаль заңы немесе Гаусс* заңы практикада жиі көп
кездесетін үлестіру заңы.
Бұл заңның басты ерекшелігі мынада, өте қатаң емес шектеулерді
сақтағанда кез келген үлестіру заңына бағынатын жеткілікті көп санды
(әлсіз тәуелді) кездейсоқ шамалар қосындысының шектік үлестіру заңы
болады (10.2-пункт).
Практикадағы есептерде қолданылатын көптеген кездейсоқ шамалар,
мысалы, өлшеулердің қателігі, техникалық құрылғыны дайындаудың
қателігі, атқыштардың қателігі және көптеген тағы басқалар, әртүрлі
факторлардың әсерінен басқалардан тәуелсіз туындайтын көп санды
элементар қателіктердің қосындысы түрінде көрсетілуі мүмкін. Осындай
кездейсоқ қателер үлестірулерінің ерекшеліктері қосындыда қосынды
нормаль заңға бағынатындай болып өзара теңестіріледі,.
Қосылғыштарға қойылатын негізгі шектеу олардың қосындыда бірдей
орын алуы – салыстырылатын шашырау талабы қойылады.
Ықтималдық тығыздығы:
2
1
f ( x )=
e
σ √2 π
−( x−m)
2
2σ
=f ( x , m, σ ) (5.8 .1)
түріндегі үзіліссіз КШ X ∈ (−∞ , ∞ ) аралықта нормаль заң бойынша
үлестірілген.
*Гаусс Карл Фридрих (1777–1855) – немістің аса көрнекті математигі, астрономы,
геодезисі. Профессор, Геттинген университетінің обсерваториясының директоры (1807–
1855). Жоғары алгебрада, сандар теориясында, дифференциалдық геометрияда,
геодезияда, аспан механикасында, электрлік және магнетизм теориясында өте тамаша
нәтижелер алды. Ең аз квадраттар әдісін, геодезияда, астрономияда дәл сынаулардағы
қателердің үлестіру заңын (Гаусс заңын) ойлап шығарды.
117.
5.8.1-сурет. Ықтималдықтың нормаль тығыздығы (Гаусс қисығы)Ықтималдықтың тығыздығы екі параметрге – m , σ (5.8.1-сурет)
тәуелді және Гаусс үлестіруінің қисығы деп аталады. Гаусс қисығының түрі
симметриялы төбе тәрізді болады. Оның максимумдық (ең үлкен)
ординатасы тең:
f ( m) =
1
={ f ( x) }max ,(5.8 .2)
σ √2 π
х=m болғанда қабылдайды (5.8.2-сурет).
Нормаль Х кездейсоқ шамасының үлестіру функциясы (5.8.2-сурет),
немесе үлестірудің нормаль функциясы:
x
f ( m) =∫ f ( t ) dt=¿
−∞
x
1
∫e
σ √ 2 π −∞
2
−(t −m)
2
2σ
dt .(5.8 .3)¿
өрнегімен беріледі.
5.8.2-сурет. Үлестірудің нормаль функциясы
x=m нүктесінде (иілу нүктесі) F(x) қисығы өсу қарқынын өзгертеді
(екінші ретті туынды теріс болады) және одан кейін бірге ұмтылады. Иілу
нүктесінің ординатасы 0,5.
m параметрін өзгерткенде f(x) және F(x) абсцисса бойымен жылжиды,
өздерінің конфигурацияларын өзгертпейді (5.8.3-, 5.8.4-суреттер).
σ параметрін өзгерткенде f(x) және F(x) қисықтары өзінің формасын
өзгертеді. σ азайғанда (Х КШ шашылуы азайғанда) жоғарыға тартылады
(5.8.3-суретті қараңыз), ал σ өскенде (Х КШ шашылуы өскенде) абсцисса
осіне қысыла майысады, бірақ Гаусс қисығының астындағы және абсцисса
осімен жасалған аудан бірге тең болады. Бұл 5.8.3-суретінен көрінеді.
Үлестірудің нормаль функциясының қисығы (5.8.4-сурет) σ азайғанда
көбірек қисық, ал




















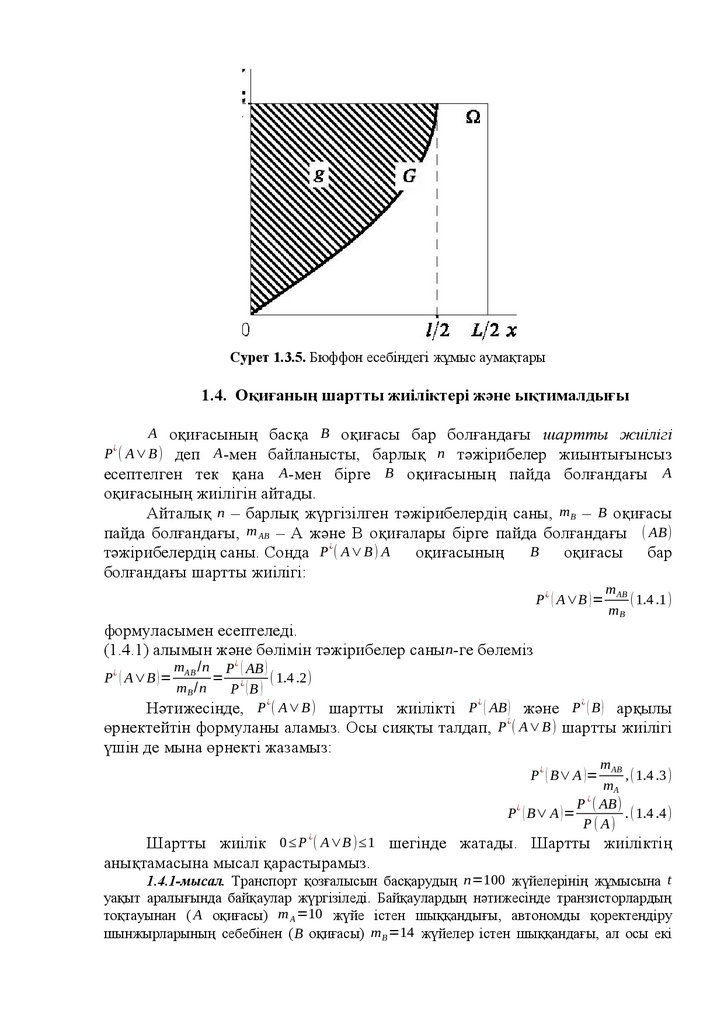


















































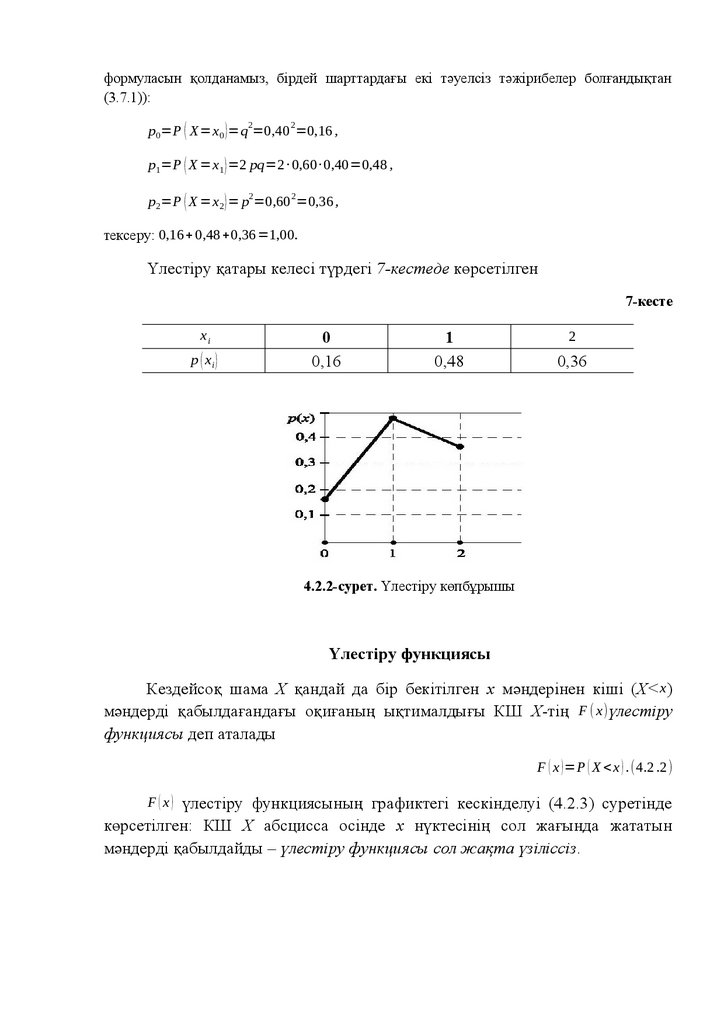











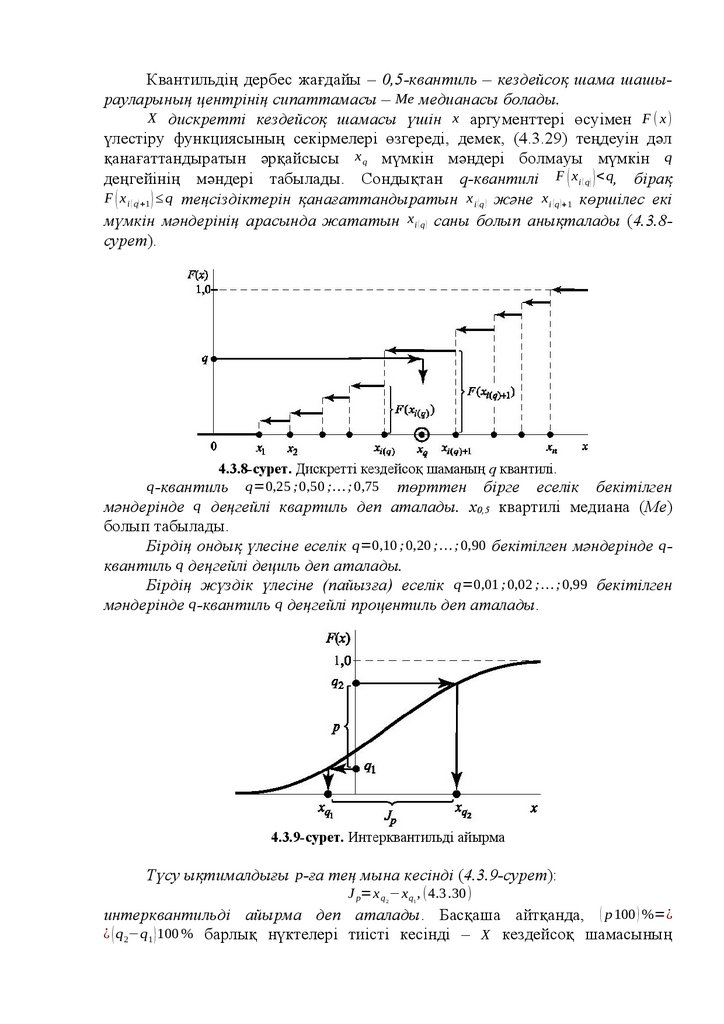

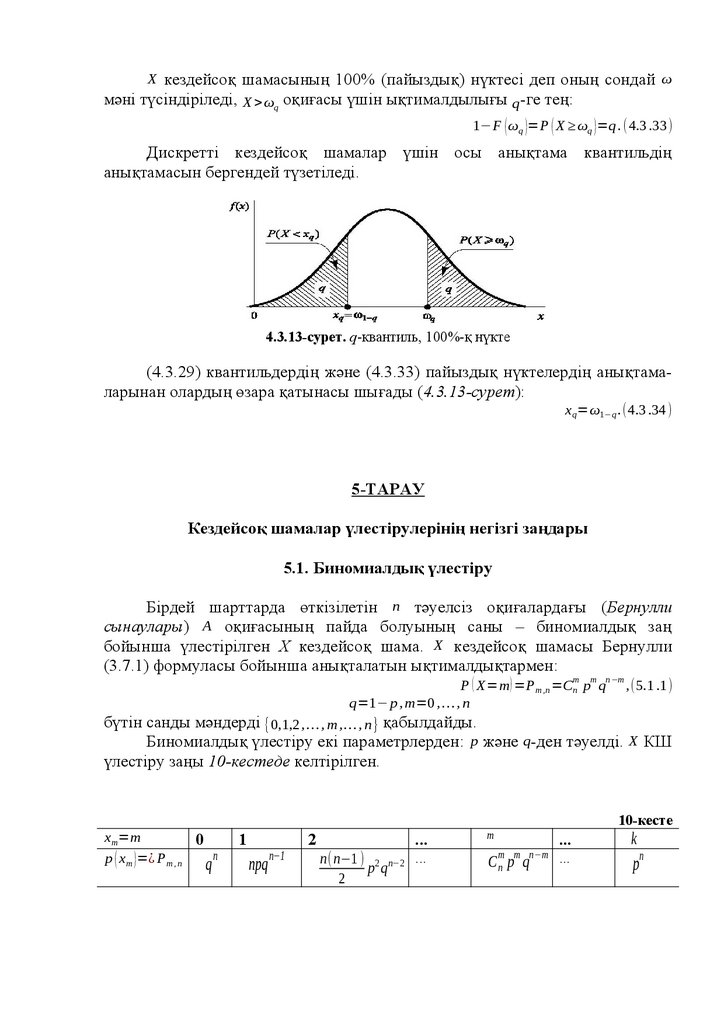



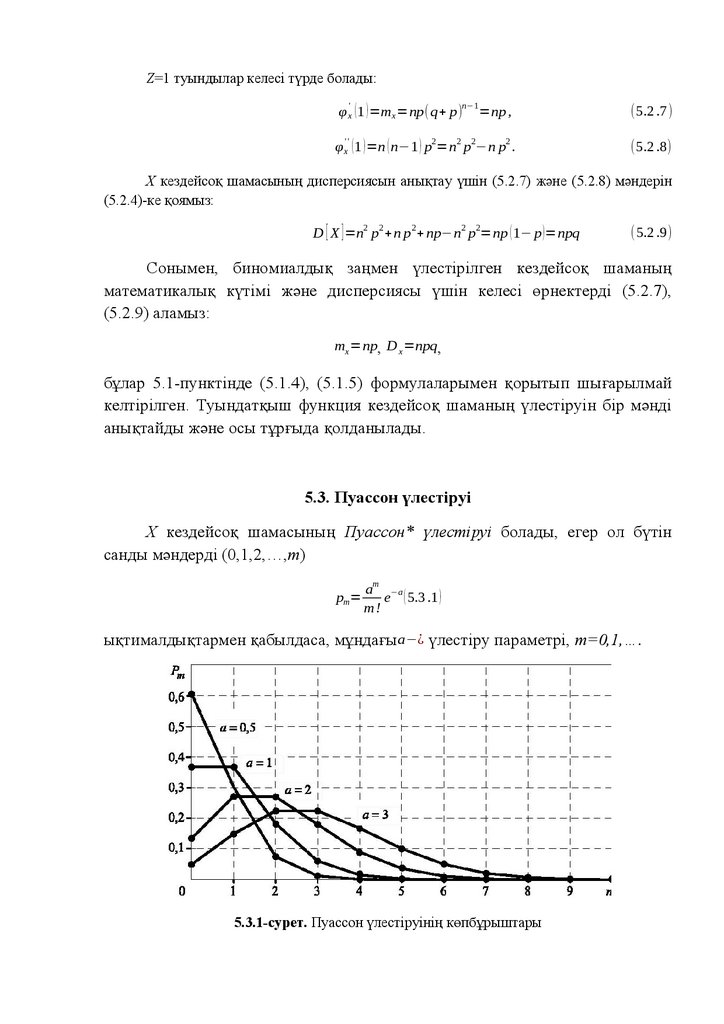










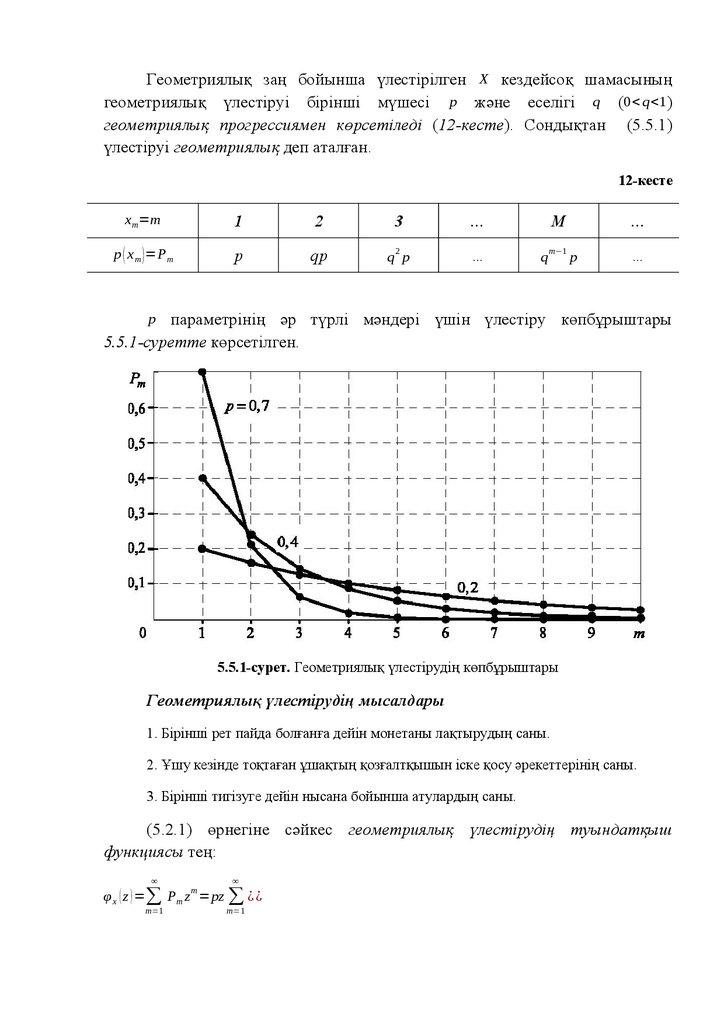


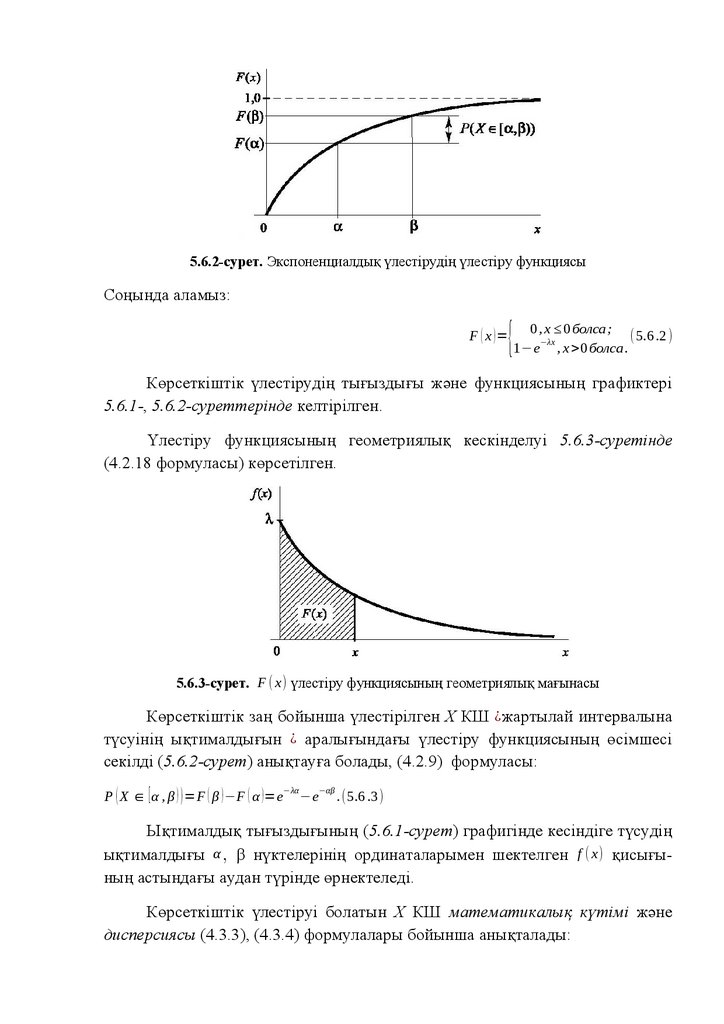





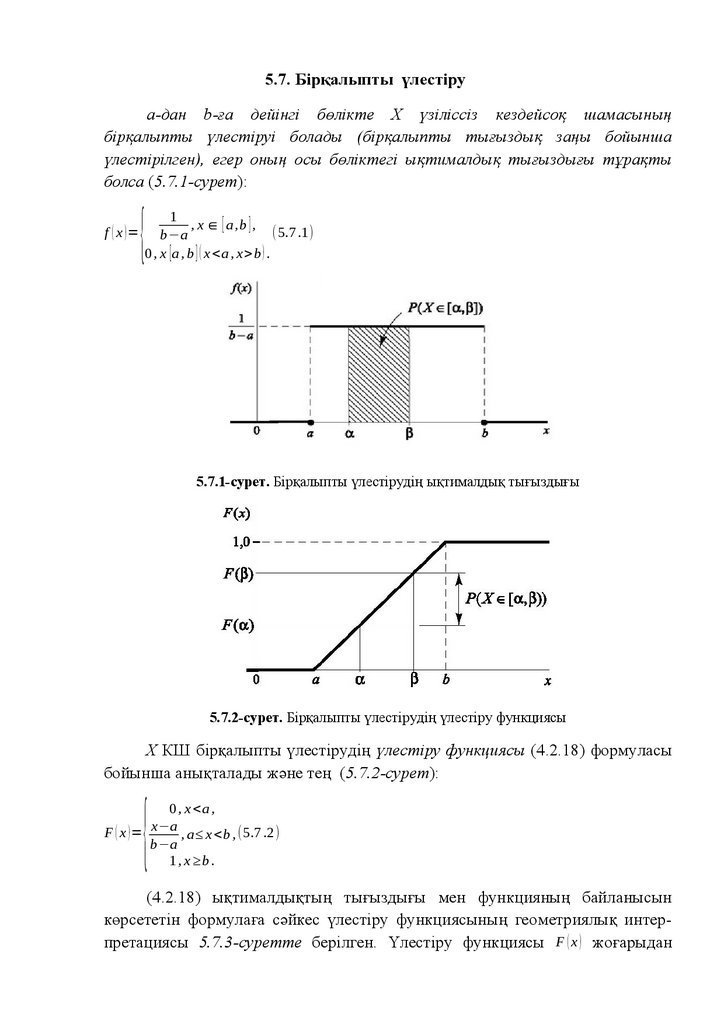





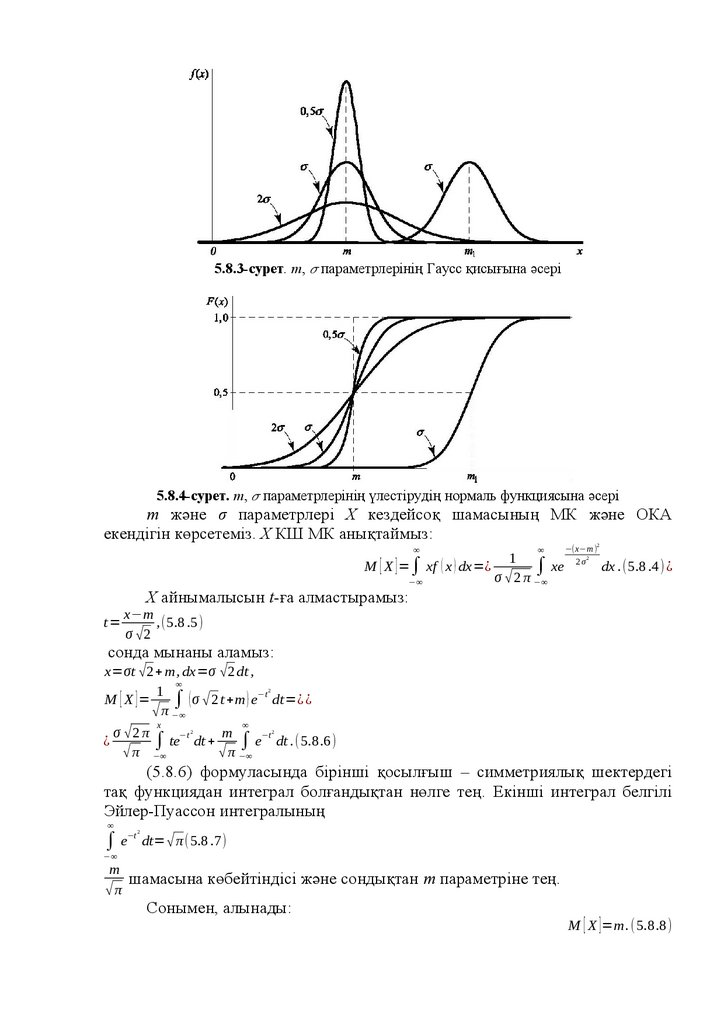

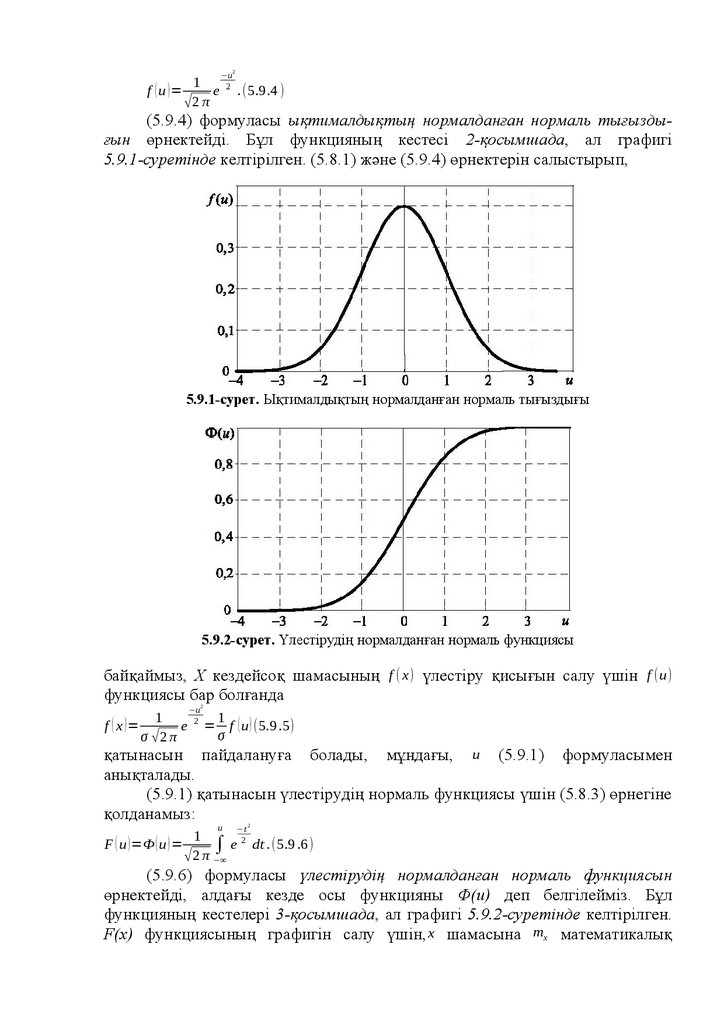











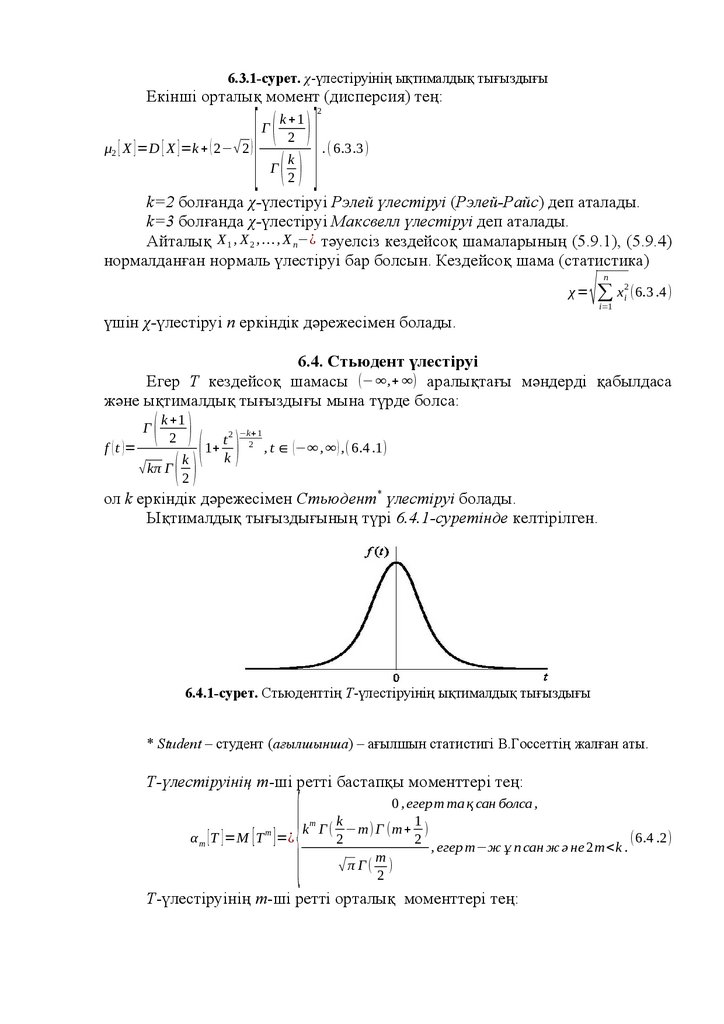




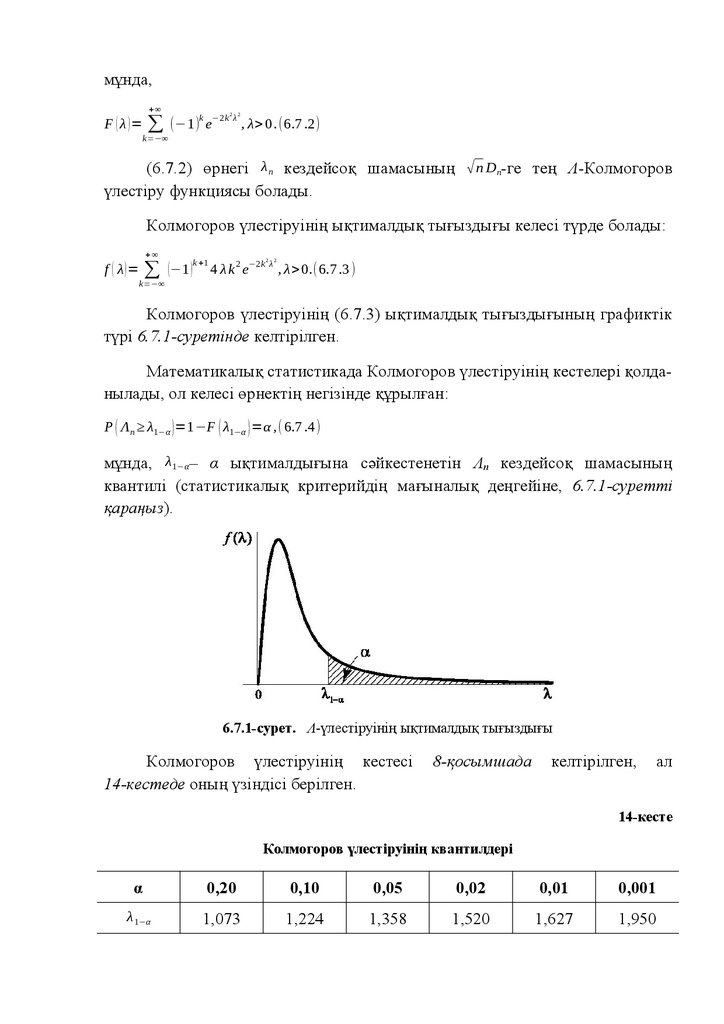







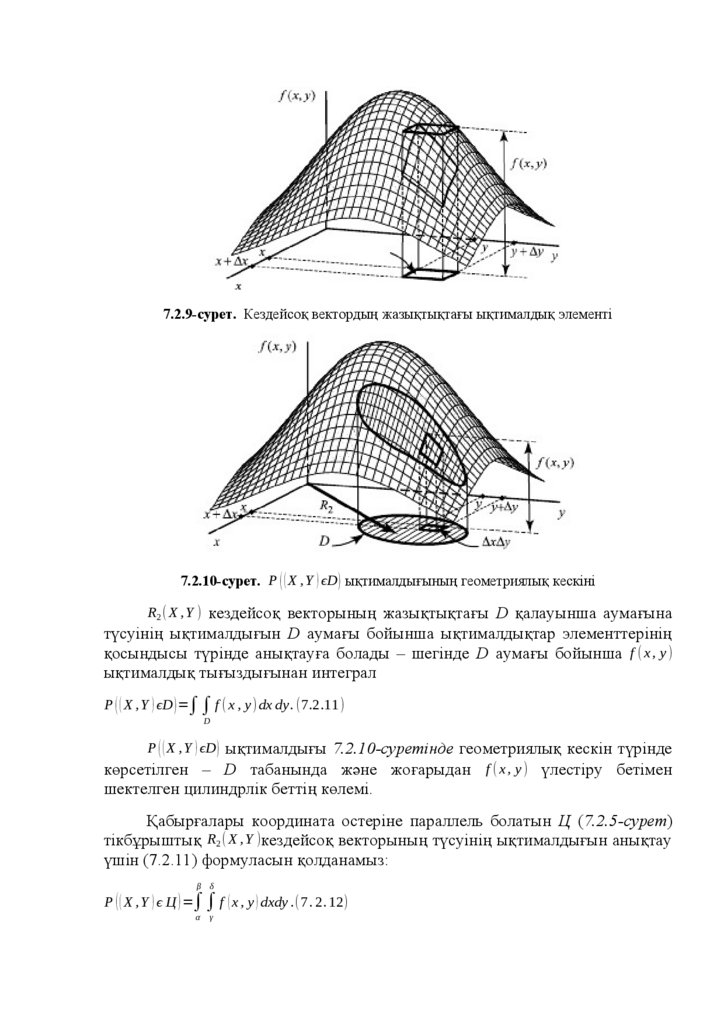












































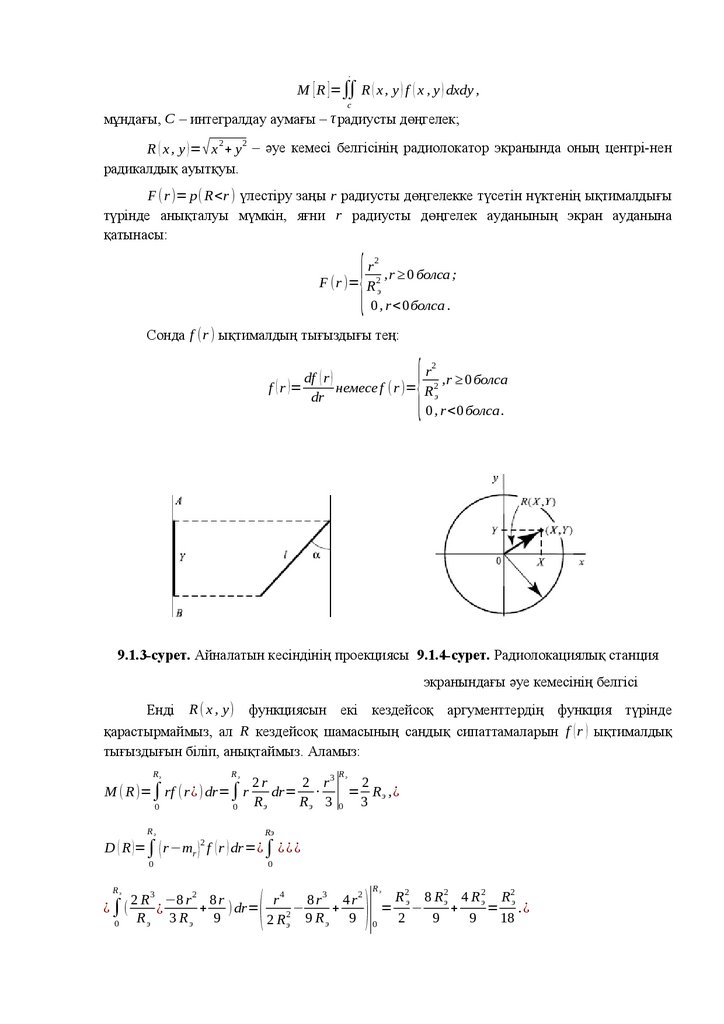


























































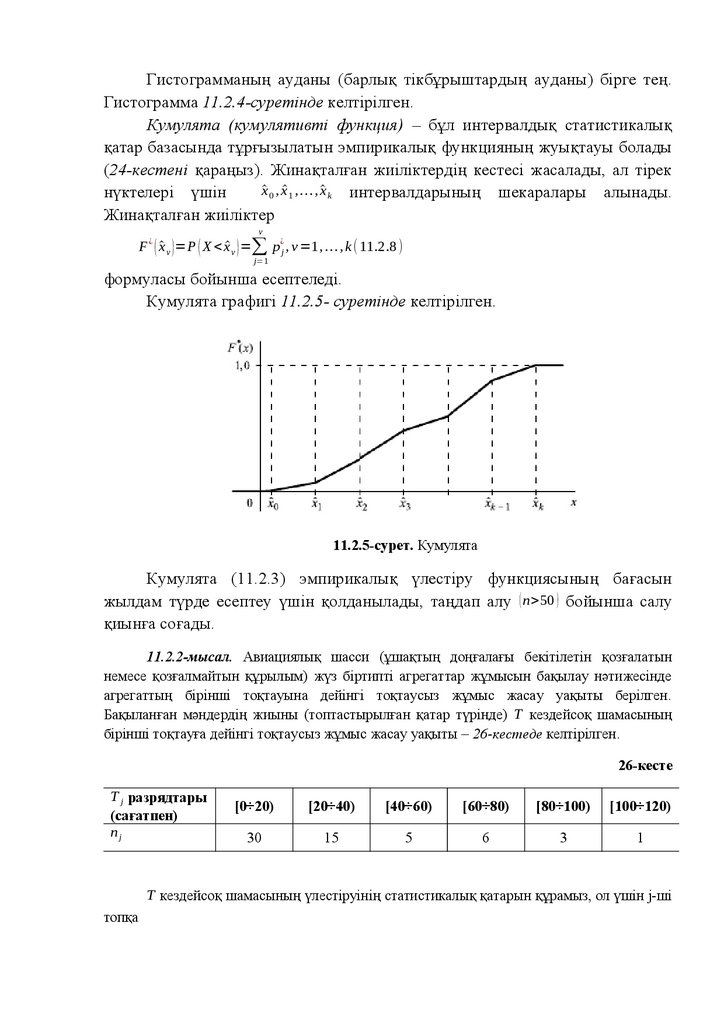
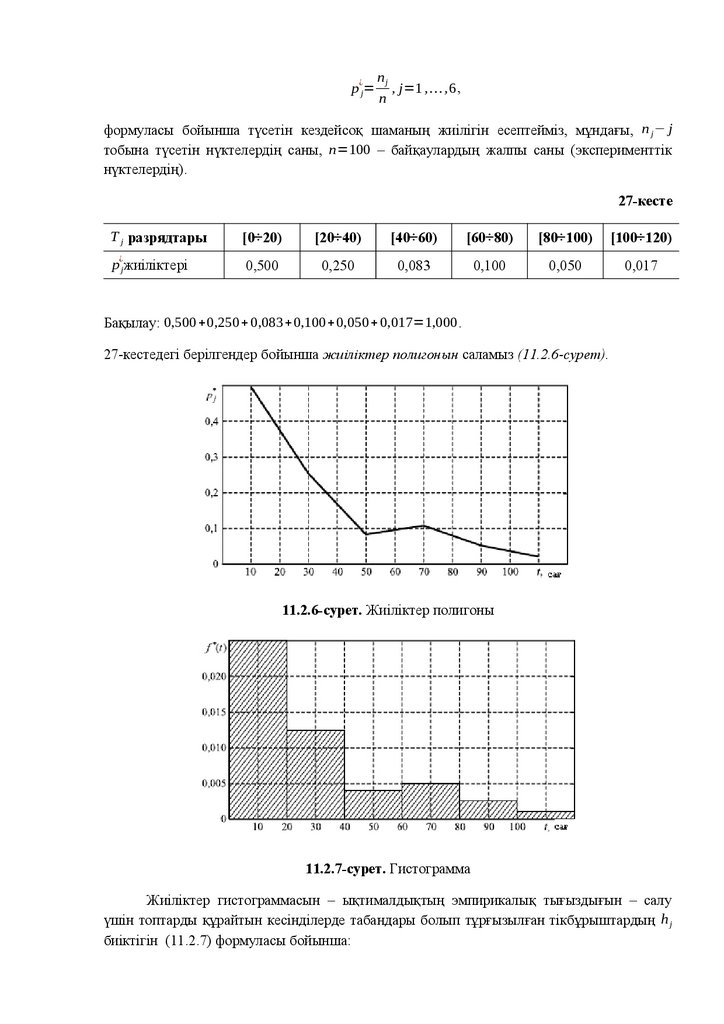
































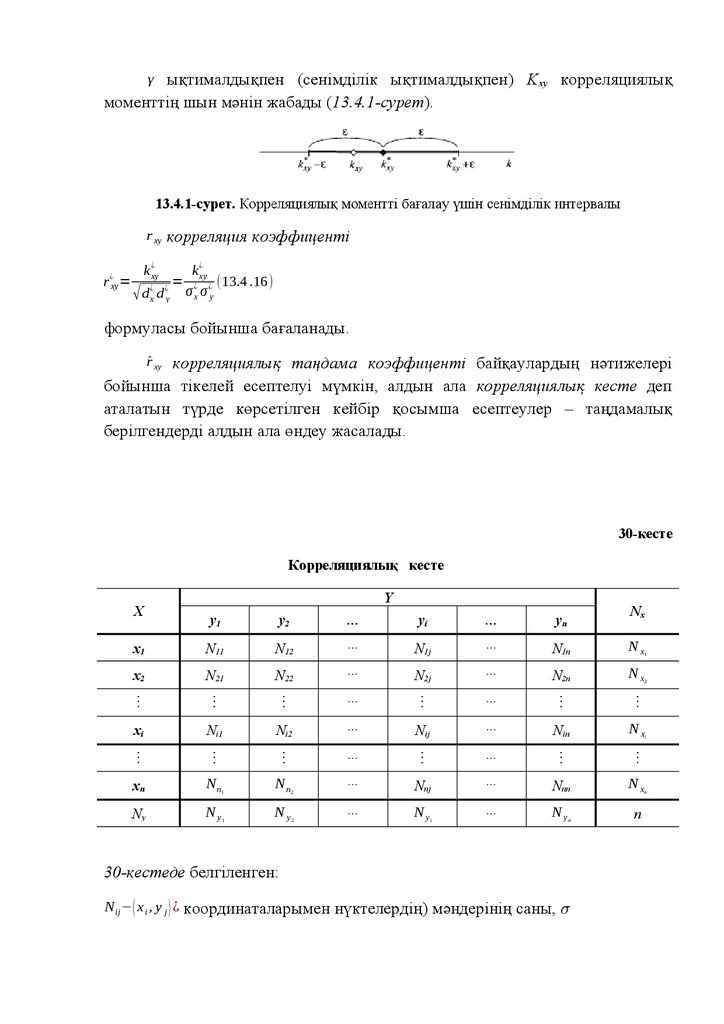








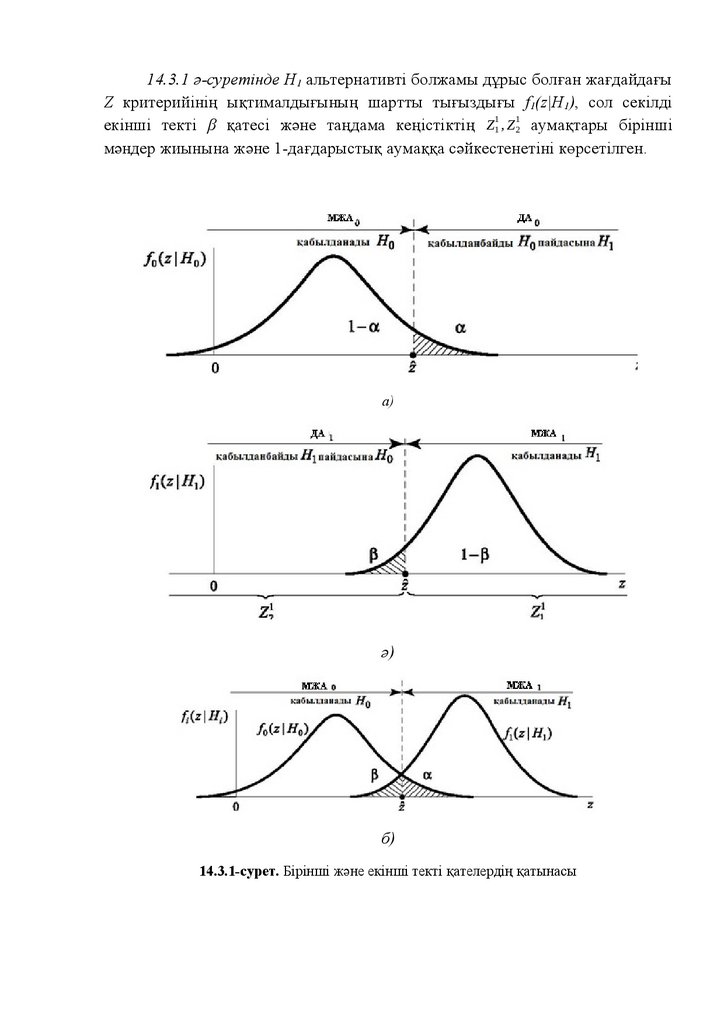










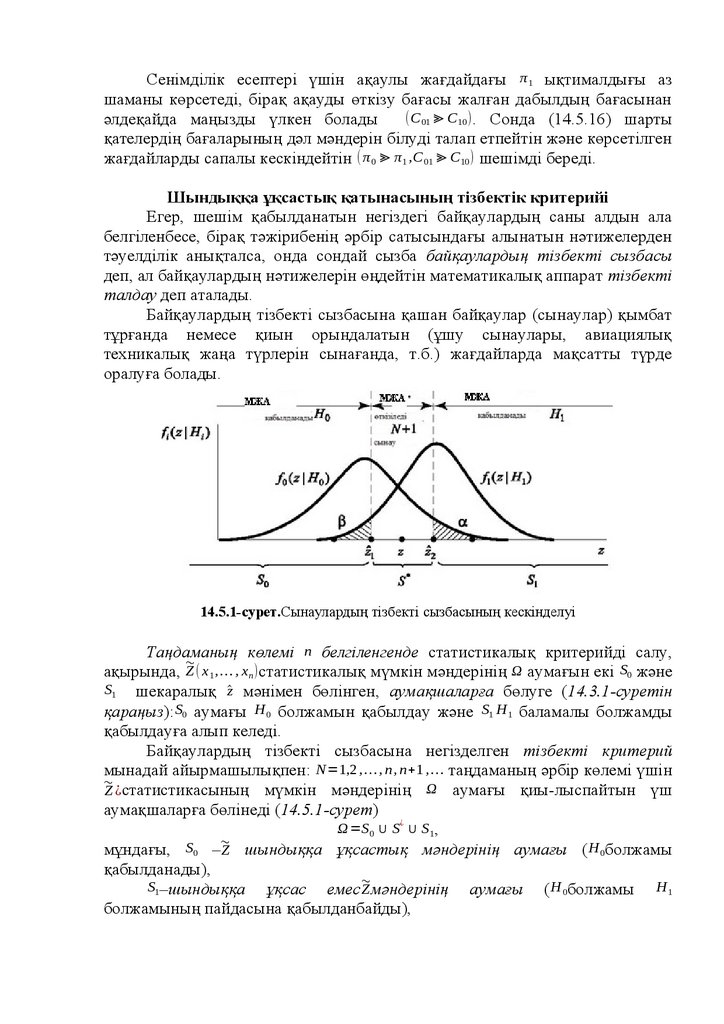




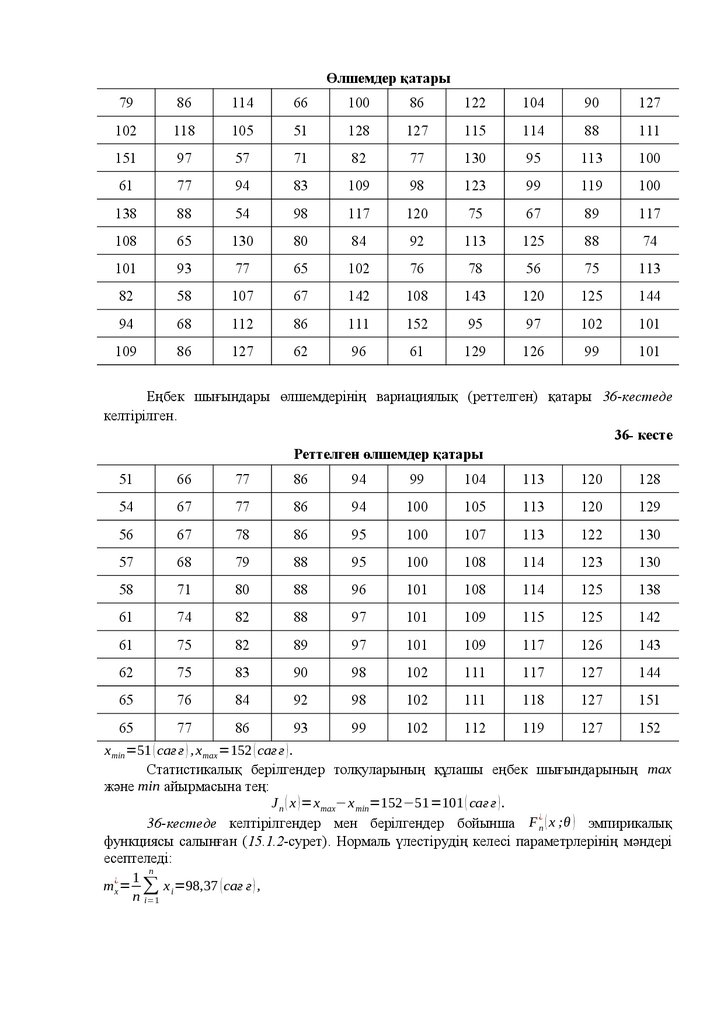
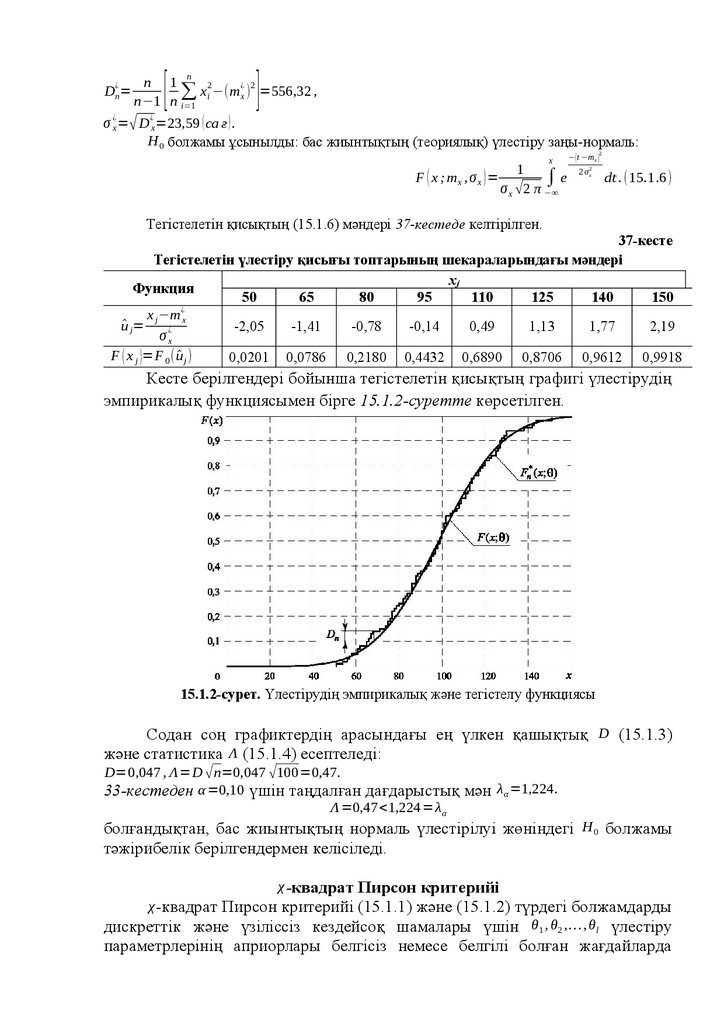






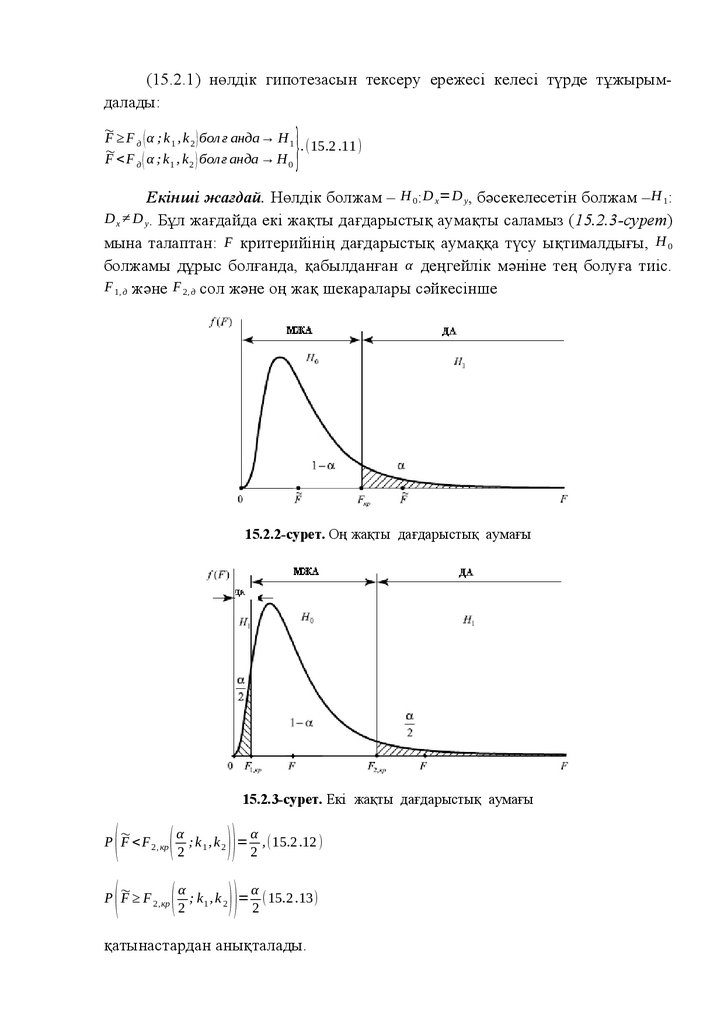













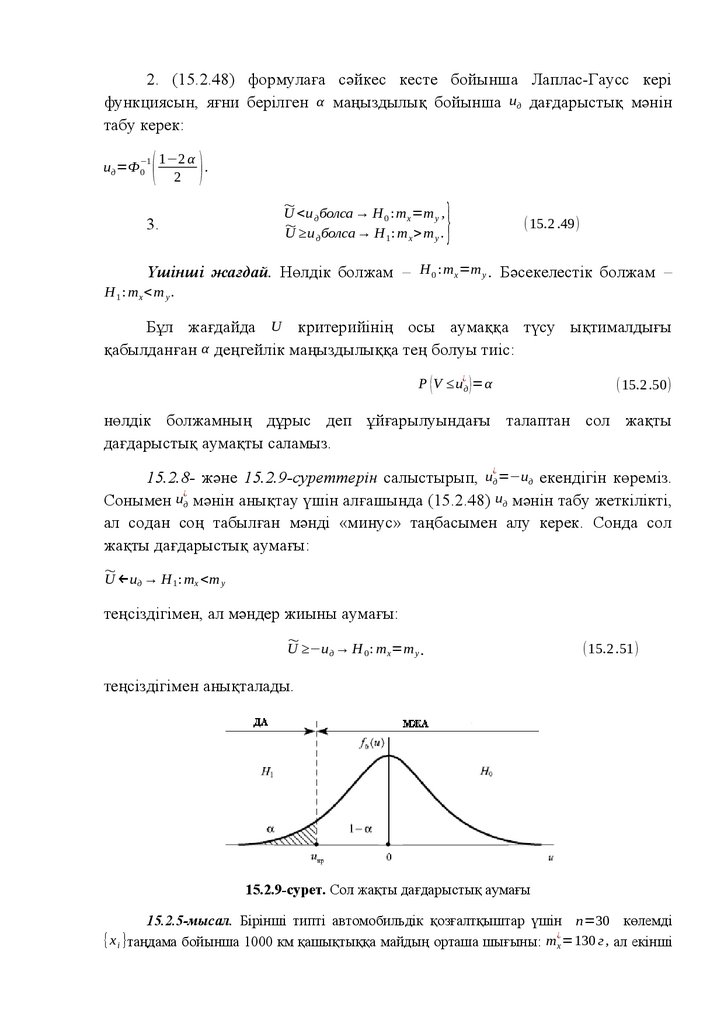


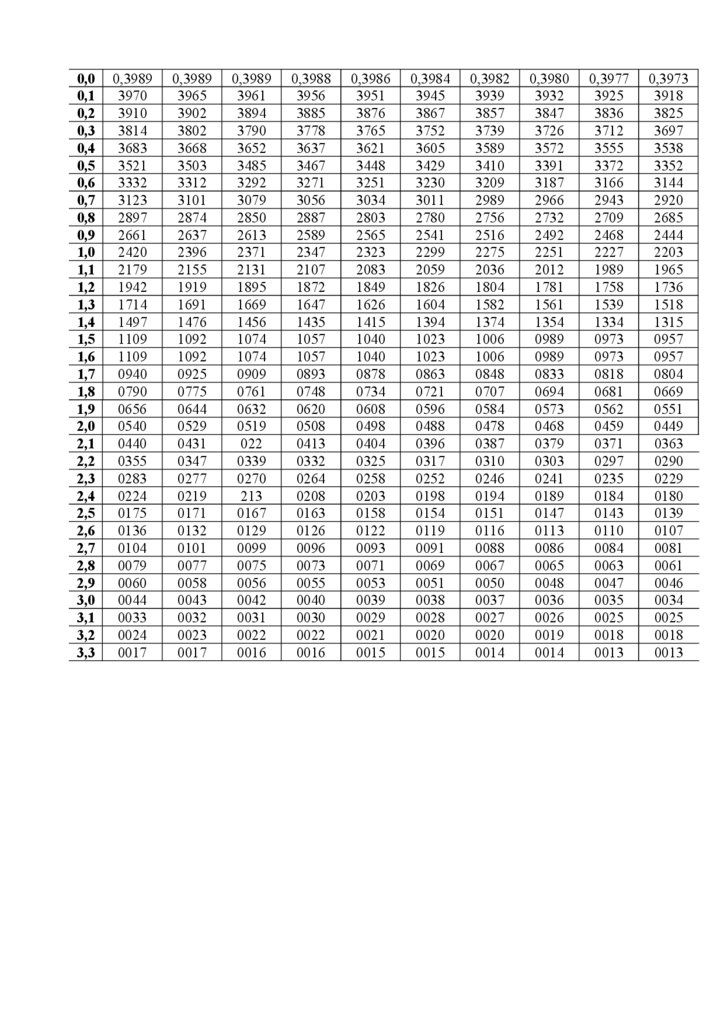
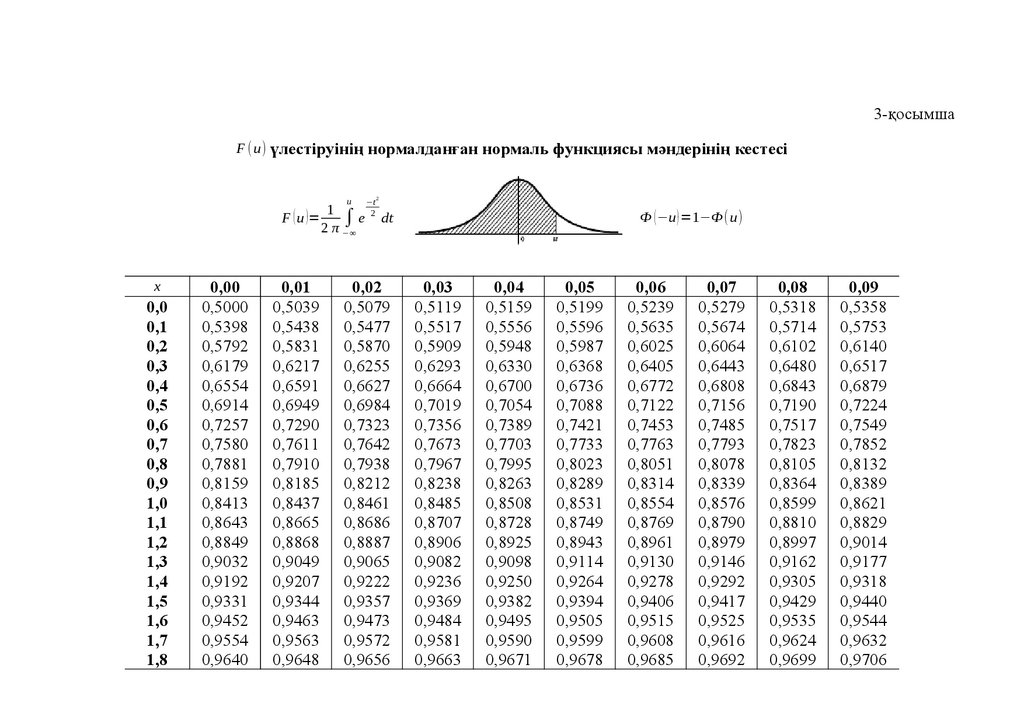

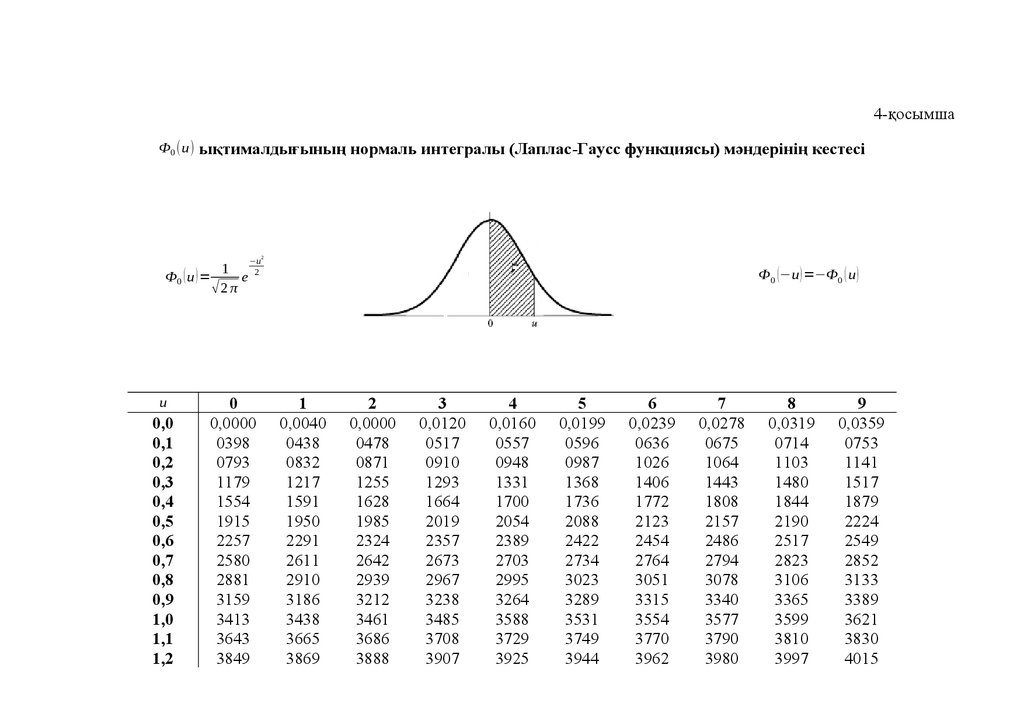
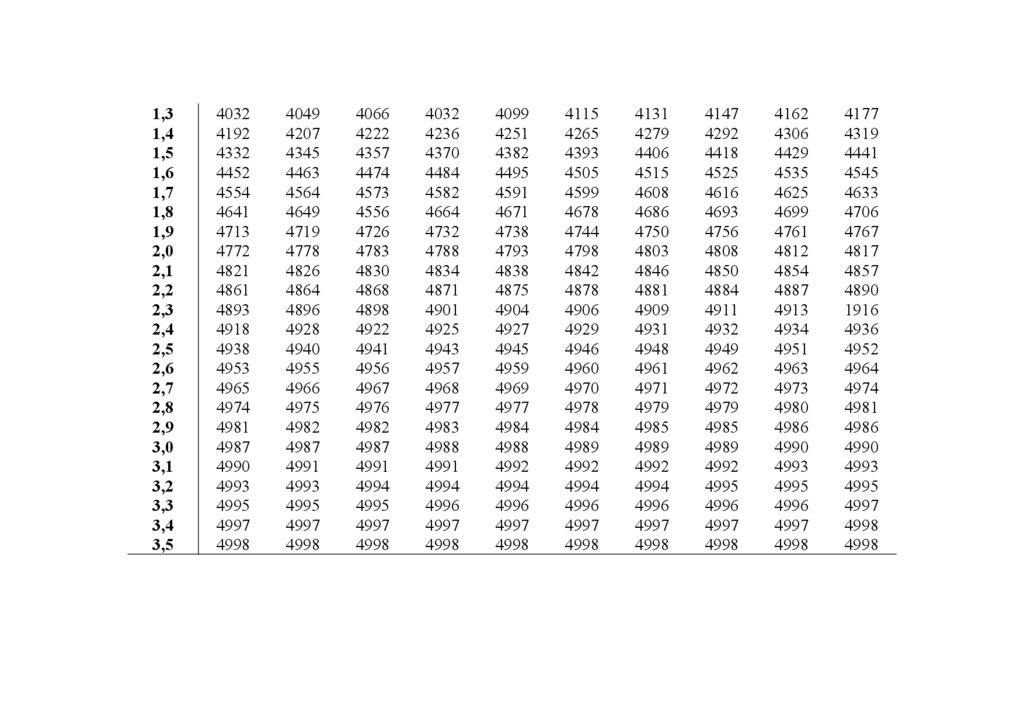
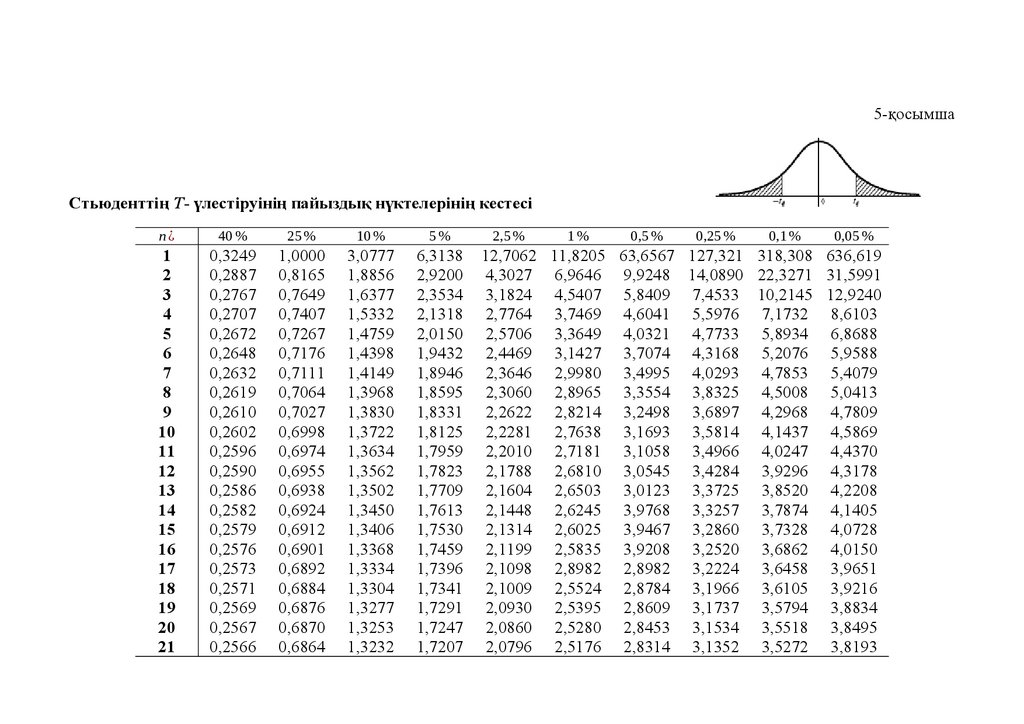


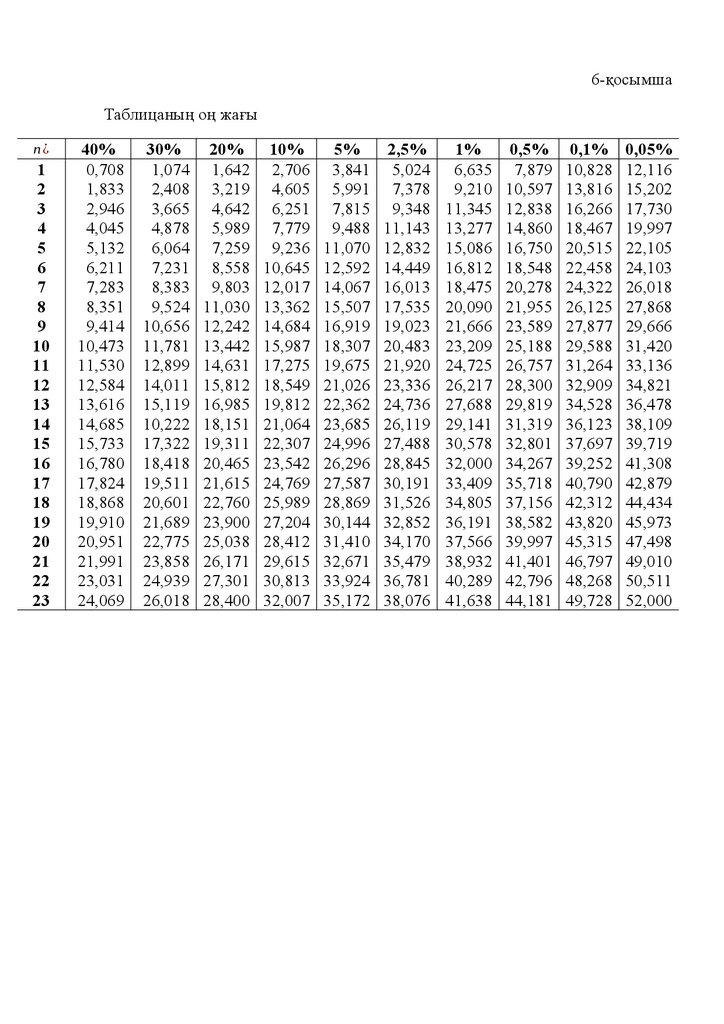




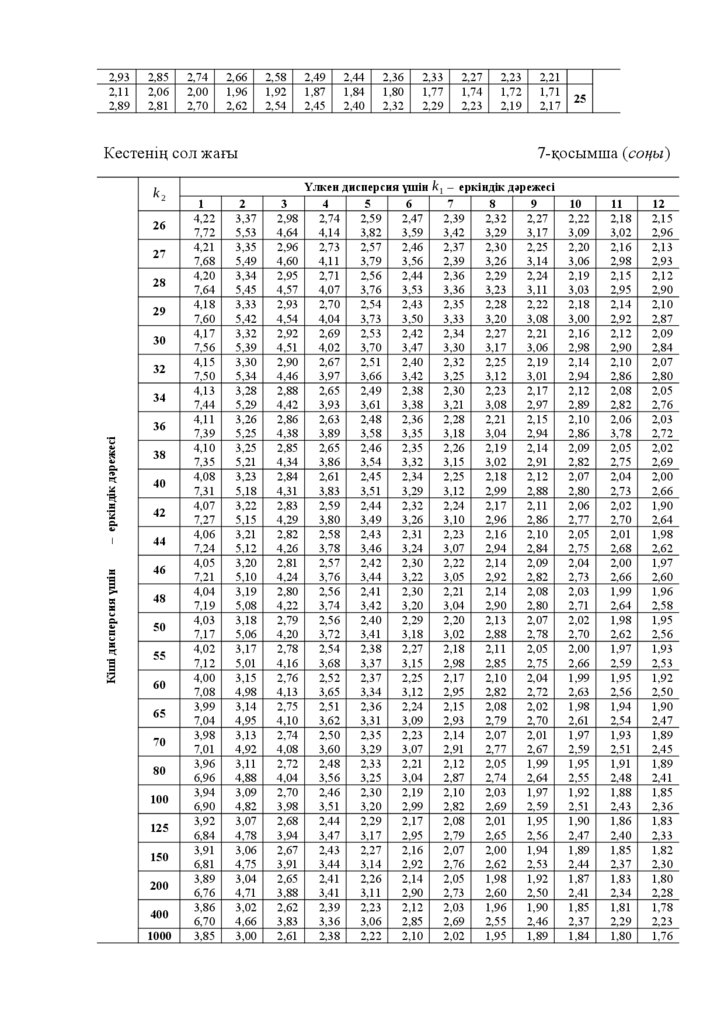
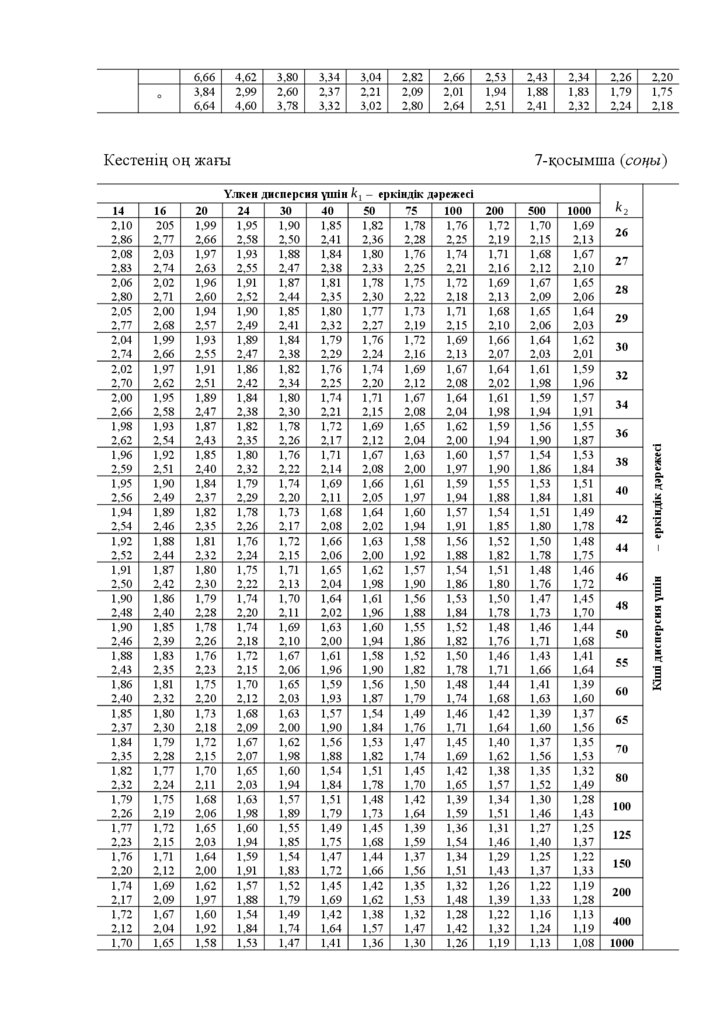

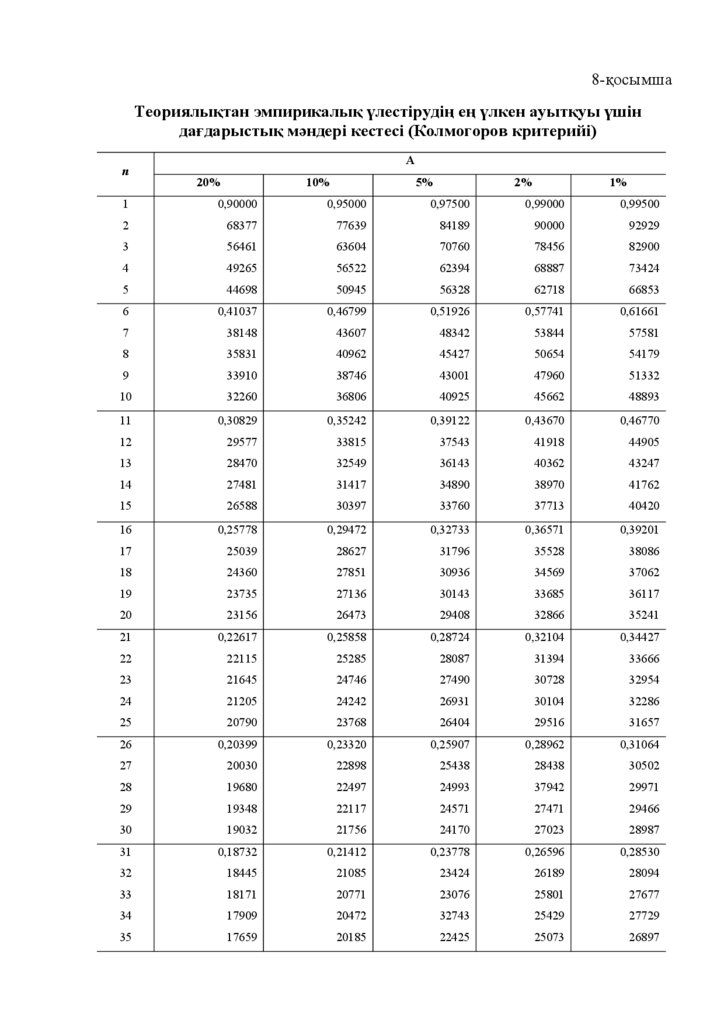
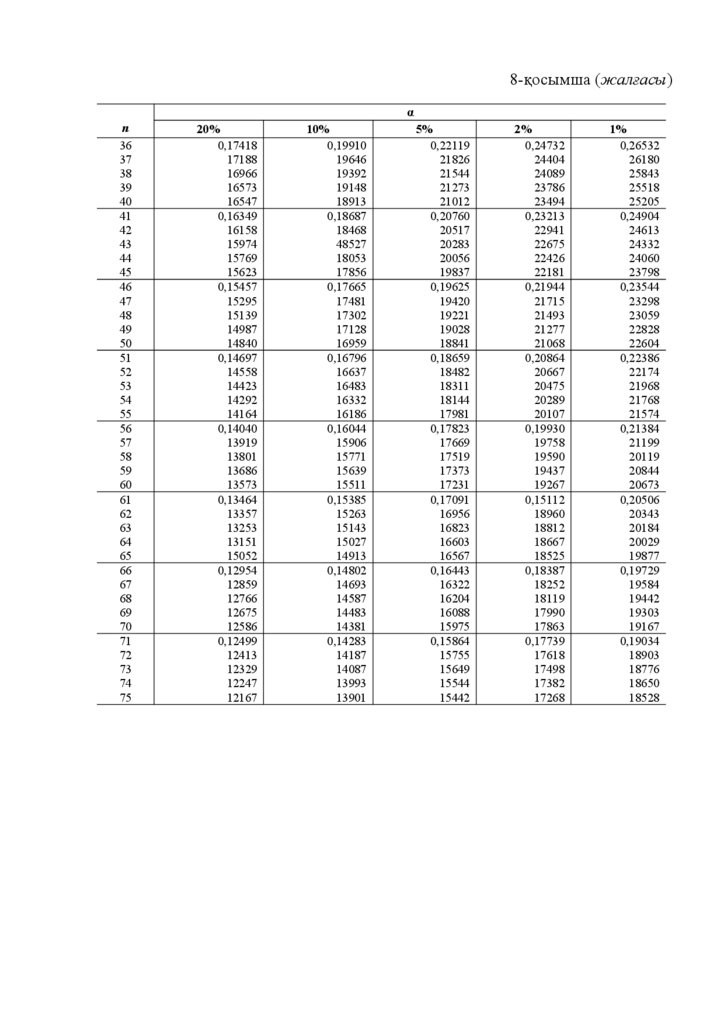



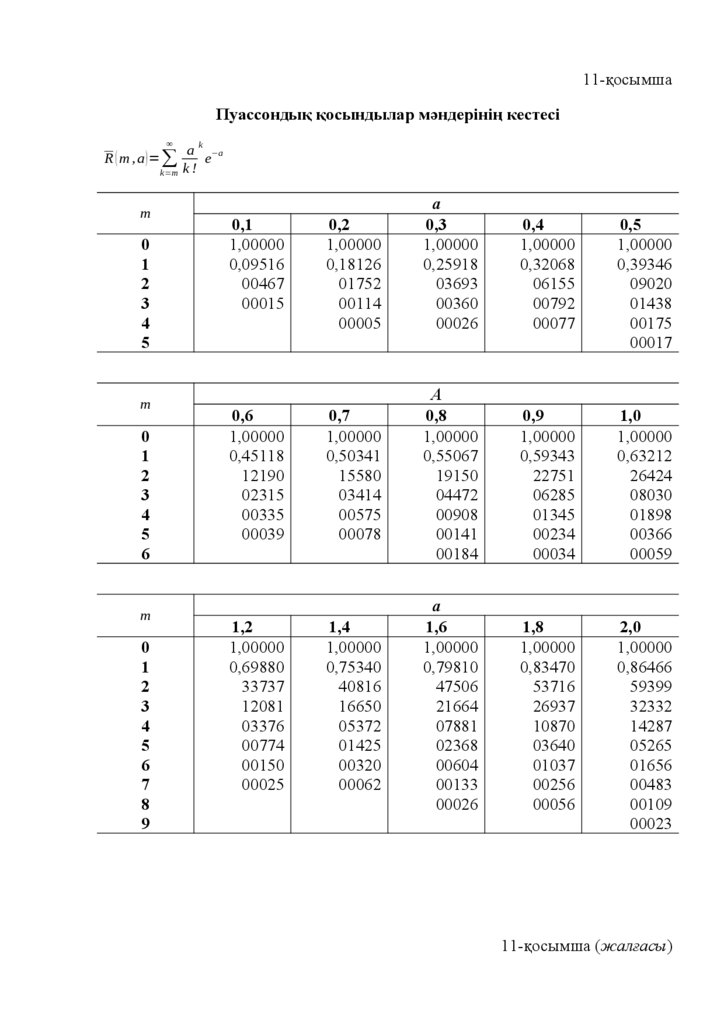














 mathematics
mathematics








