Similar presentations:
Үзіліссіз кездейсоқ шамалар
1. А. Байтұрсынов атындағы Қостанай Мемлекеттік Университеті Аграралық-техникалық институт Математика және физика кафедрасы
Математика 3 пәніМатематика және физика кафедрасының аға
оқытушысы , Берденова Г.Ж.
Қостанай, 2020
2. Тақырып: Үзіліссіз кездейсоқ шамалар
3. Мақсат:
Үзіліссіз кездейсоқ шаманыңүлестiрiм заңдарымен және
сандық
сипаттамаларымен
танысу.
4. Қарастырылатын сұрақтар:
1. Кездейсоқ шамалар және үлестiрiм заңдары.2. Кездейсоқ шаманың үлестiрiм функциясы
және оның қасиеттерi.
3. Кездейсоқ шаманың үлестiрiм тығыздығы
және оның қасиеттерi.
4. Үзiлiссiз кездейсоқ шамалар.
5.Үзiлiссiз кездейсоқ шаманың негiзгi үлестiрiм
заңдары.
6. Үзiлiссiз кездейсоқ шаманың сандық
сипаттамалары.
5. 1 Анықтама.
Кездейсоқ себептен тәуелдi,алдын-ала белгiсiз бiр мүмкiн
мәндi тәжiрибе нәтижесiнде
қабылдайтын шама кездейсоқ
деп аталады.
6. 2 Анықтама.
Мәндерi саналатын жиынқұратын шама (элементтерiн
нөмiрлеуге болатын жиын)
дискреттiк кездейсоқ шама
деп аталады.
7. Анықтама.
Кейбiр шектелген немесешексiз интервалдан кез
келген мән қабылдайтын
шама үзiлiссiз кездейсоқ
шама деп аталады.
8. 3 Анықтама.
Кездейсоқ шаманың мүмкiн мәндерiмен сәйкес ықтималдықтары
арасындағы қатынасты
тағайындайтын заң кездейсоқ
шаманың үлестiрiм заңы деп аталады.
• Үзiлiссiз кездейсоқ шаманың үлестiрiм
заңы үлестiрiм функциясы немесе
үлестiрiм тығыздығы арқылы берiлуi
мүмкiн.
9. Анықтама.
Хкездейсоқ
шамасының
ықтималдықтарының
үлестiрiм
функциясы (немесе
интегралдық
функциясы, үлестірім заңы) F(x) деп
х-тiң әрбiр мәнi үшiн Х -кездейсоқ
шамасы (X<x)
х-тен кем мән
қабылдау ықтималдығын анықтайтын
функция аталады: F ( x) P( X x)
10. Анықтама.
Хкездейсоқ
шамасының
ықтималдықтарының
үлестiрiм
функциясы (немесе
интегралдық
функциясы, үлестірім заңы)
F ( x ) P( X x )
деп х-тiң әрбiр мәнi үшiн Х -кездейсоқ
шамасы
х-тен кем мән қабылдау
ықтималдығын анықтайтын F (x )
функция аталады:
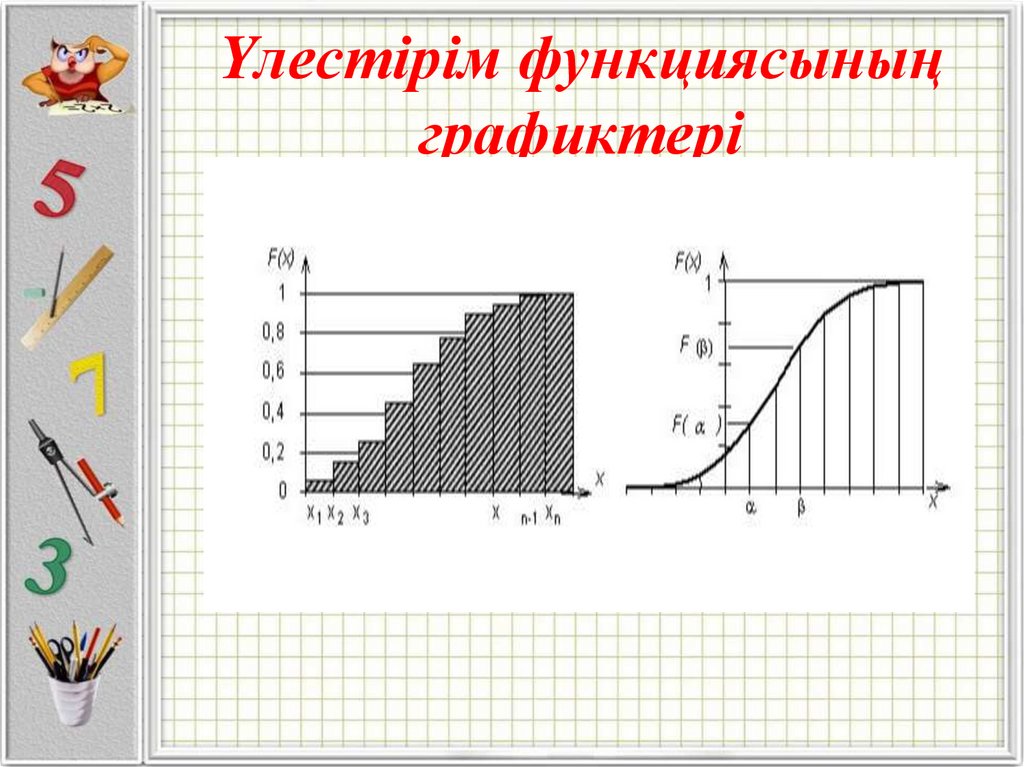
11. Үлестірім функциясының графиктері
12. Үлестiрiм функциясының қасиеттерi:
..
Үлестiрiм функциясының
қасиеттерi:
1. Функция мәндерi [0,1] кесiндiсiне тиiстi:
0 F ( x) 1
2. Үлестiрiм функциясы кемiмейтiн функция:
егер х2> х1 болса F ( x ) F ( x )
2
1
3. Егер Х кездейсоқ шамасының барлық
мүмкiн мәндерi (а;в) интервалына тиiстi
болса, онда х а болғанда
F(x)=0 және
х в болғанда F(x)=1.
13.
Салдар 1.P( X ) F ( ) F ( )
Салдар 2.
Х үзiлiссiз кездейсоқ шамасының нақты
бiр мән қабылдау ықтималдығы нольге
тең.
Салдар 3.
Егер Х - кездейсоқ шамасының мүмкiн
мәндерi осьтiң барлық бойында
орналасса, онда
lim
x
F(x)=0, lim
x
F(x)=1.
14. Анықтама.
Үлестiрiм функциясыныңтуындысы ықтималдықтар
үлестiрiмiнiң тығыздығы деп
аталады:
f ( x) F ( x)
15. Теорема.
Х- үзiлiссiз кездейсоқшамасының интервалынан мән
қабылдау ықтималдығы мына
формуламен анықталады:
P( X ) f ( x)dx
16. Үлестiрiм тығыздығының негiзгi қасиеттерi:
1. Үлестiрiм тығыздығы терiсемес функция: f(x) 0.
2. Интегралдау шегi барлық сан
осi болғанда үлестiрiм
тығыздығының меншiксiз
интегралы бiрге тең:
f ( x ) dx 1
17. Үздіксіз кездейсоқ шаманың сандық сипаттамалары:
М (Х )x f ( x ) dx
D(Х ) x M ( X )
2
f ( x) dx
анықтама бойынша
D( X )
x
f
(
x
)
dx
M
(
X
)
2
2
- теорема бойынша
18. Кездейсоқ шамалардың үлестірім заңдары:
19. Бiрқалыпты үлестiрiм заңы –
кездейсоқ шаманың мүмкiнмәндерiнiң интервалында
үлестiрiм тығыздығы өзгермейтiн
үлестiрiм:
1
, егер а х в
f ( x) в а
0, егер х а, х в
20. Көрсеткiштiк (экспоненталық) үлестiрiм заңы –
– параметрi болатын үлестiрiм,егер ықтималдықтар тығыздығы
мына түрде болса:
е , егер х 0
f ( x)
егер х 0
0,
х
21. Қалыпты үлестiрiм заңы (Гаусс заңы)
параметрлерi а және , егер оныңықтималдықтар тығыздығы мына
түрде болса:
f ( x)
1
2
e
( x a)2
2 2
22.
Параметрлерi а=0, σ =1болатын кездейсоқ
шаманың қалыпты
үлестiрiм заңы
стандартты немесе
мөлшерленген деп
аталады.
23.
Мөлшерленген үлестiрiмнiңықтималдықтар тығыздығы мына
түрде болады:
f ( x)
1
e
2
x2
2
функциясы Лапластың локалдық
функциясы деп аталады.
24.
2.Теорема.
Қалыпты заңмен үлестiрiмдi Х кездейсоқ шамасының
М(Х) = а,
D(Х) =
2
25.
2.Х қалыпты үлестiрiмдi шамасы
( , )
интервалына тиiстi мән
қабылдау ықтималдығы:
а а
Р( X ) Ф
Ф
мұнда Ф (х) – Лаплас интегралдық
функциясы.
26.
2.Қалыпты кездейсоқ шаманың
өз математикалық үмiтiнен ауытқуы
0 шамасынан кем болу
ықтималдығы мынаған тең:
P( X a ) 2Ф
27. Мысал
28.
29.
30.
31.
32.
33.
34.
35.
36. Тексеруге арналған сұрақтар:
37. Ұсынылатын әдебиеттер тізімі
38.
Назарларыңызғарахмет!





































 mathematics
mathematics physics
physics








