Берілген үлестіру заңымен кездейсоқ сандарды модельдеу

1.

Қазақстан Республикасы білім және ғылым министрлігі
Әл - Фараби атындағы Қазақ Ұлттық Университеті
Факультеті «____________ЭжБЖМ___________________»
Кафедрасы «__________Бизнес технология________________»
СЕМИНАР-2
Тақырыбы:Берілген үлестіру заңымен кездейсоқ сандарды
модельдеу

2.

Алматы, 2021ж
ЖОСПАР:
1. Кіріспе.
2. Негізгі бөлім.
2.1. Кездейсоқ сандарды берілген үлестіру заңына сәйкес бөлінген
кездейсоқ сандар түріне ауыстыру.
2.2. Берілген үлестіру заңымен кездейсоқ сандарды модельдеу.
2.3. Берілген үлестіру заңымен кездейсоқ сандарды модельдеудің
әдістері.
2.3.1. Қадамды аппроксимация әдісі.
2.3.2. Кері функцияны қабылдау әдісі.
3. Қорытынды.
4. Пайдаланылған әдебиеттер.

3.

1. Кіріспе.
Х кездейсоқ шамасының ықтималдылықтың таралу заңы экономист үшін
математикалық күту және дисперсия сияқты статистикалық сипаттамалармен
салыстырғанда анағұрлым ақпараттылықты білдіреді.
Қазіргі кезде стандартты моделдеу кітапханалық бағдарламалардың
барлығы дерлік Леммерәзірлеген біркелкі кездейсоқ сандар конгруент
әдістеріне негізделген.
Мультипликативті Леммер әдісініңнегізгі формуласы:
Ri+1 = aRi(mod m)
мұндағы а және m - теріс емес бүтін сандар.
Осы өрнек бойынша кездейсоқ Ri санын алып, оны тұрақты а
коэффициентіне көбейту керек, және алынған саннан модуль m-ді аламыз
(яғни aRi-ге бөлу және оның Ri + 1 қалдығы)
Сондықтан Ri тізбегін есептеу (немесе генерациялау) үшін бізге бастапқы
мәндер R0, факторы және m модулі қажет. а, R0 және m максималды
ұзындықты (кезеңді) қамтамасыз ету үшін әрі қайталанбайтындай және Ri
тізбектері және алынған сандар арасында минималды корреляция
болатындай таңдалады.
Базистік кездейсоқ сандаркез-келген тарату заңына бағынатын жаңа
кездейсоқ тізбектер жасауға мүмкіндік береді.
Бақылау нәтижелерінің статистикалық сипаттамасы тұжырымдаманы
қолдана отырып әр түрлі математикалық модельдерді құру және тексеруге
мүмкіндік береді.
Мұндағы, ықтималдықтар - бұл математикалық статистиканың негізгі
мазмұны.
Көптеген қолданбалы мәселелерді шешу кезінде қажетті ықтималдық
сипаттамалар кездейсоқ шамаларды зерттеушіге белгісіз және оларды
эксперименттік мәліметтер бойынша анықтау керек.
Өндірісте және технологияда мұндай
проблемалық жағдаяттарда сәйкес көрсетіледі.
тарату
заңдары
көбінесе

4.

Біздің ендігі міндетіміз - белгілі бір кездейсоқ оқиғалардың пайда
болуын осындай үлестіру ықтималдығына сәйкес модельдеуді үйрену.
2. Негізгі бөлім.
2.1.
Кездейсоқ сандарды берілген үлестіру заңына сәйкес бөлінген
кездейсоқ сандар түріне ауыстыру.
{Ri} базистік кездейсоқ сандарды берілген үлестіру заңына сәйкес
бөлінген кездейсоқ сандар {yi} түріне ауыстырудың екі негізгі әдісі бар:
Оның бірі инверсия әдісі деп аталады, ол yi алу үшін Ri базалық санымен
арифметикалық амалдар орындалуынан тұрады
Екінші әдіс шектік
ықтималдықтар теоремалары.
2.2.
шарттарын
модельдеуге
негізделген
Берілген үлестіру заңымен кездейсоқ сандарды модельдеу.
Х белгілі бір диапазоннан кездейсоқ мәндерді алады деп елестетейік.
Мысалы, Х - өңделген бөліктің диаметрі.
Диаметр әр түрлі факторлардың әсерінен жоспарланған идеалды мәннен
ауытқуы мүмкін, оларды ескеруге болмайды, сондықтан бұл кездейсоқ,
нашар болжанатын мән. Бірақ өндірілген бөлшектерді ұзақ уақыт бақылау
нәтижесінде 1000-дан қанша бөліктің диаметрі X1 болғанын (NX1
белгілейміз), қанша бөлшектің диаметрі X2 болғанын (NX2 белгілейміз) және
т.с.с. атап өтуге болады.
Нәтижесінде, диаметрлер жиілігінің гистограммасын құруға болады:
X1 үшін NX1 / 1000 мәнін, X2 үшін NX2 / 1000 мәнін және т.б. (дәлірек
айтқанда, NX1 - бұл диаметрі X1-ге тең емес, бірақ X1 - Δ / 2-ден X1 + Δ / 2ге дейінгі бөліктердің саны, мұндағы Δ = X1 - X2).
Барлық жиіліктердің қосындысы 1-ге тең болуы маңызды
(гистограмманың жалпы ауданы өзгермеген). Егер Х үздіксіз өзгеріп отырса,
көптеген эксперименттер жүргізілген болса, онда N -> ∞ шегінде
гистограмма кездейсоқ шаманың ықтималдылық таралуының графигіне
айналады.
Төменде, а дискретті үлестірім гистограммасының мысалын көрсетеді,
және сурет b кездейсоқ шаманың үздіксіз таралуының нұсқасын көрсетеді.

5.

Мысалда кездейсоқ шаманың ықтималдылықтың таралу заңы өндірілген
бөлшектер диаметрінің белгілі бір мәнінің қаншалықты ықтимал екендігін
көрсетеді. Мұндағы, бөлшектің диаметрі - кездейсоқ шама.
2.3.
Берілген үлестіру заңымен кездейсоқ сандарды модельдеудің
әдістері.
2.3.1. Қадамды аппроксимация әдісі
Әдіс функция аналитикалық жолмен (формула түрінде) берілген кезде
қолданылады. Функцияның графигі тіктөртбұрышты салынған.
Графиетегі RNG-тен кездейсоқ, біркелкі бөлінген сан Y осіне беріледі.
Екінші RNG-тен кездейсоқ, біркелкі бөлінген сан Х осіне беріледі. Егер осы
екі координатаның қиылысында нүкте ықтималдық тығыздығының
қисығының астында жатса, онда Х оқиғасы орын алады.
Әдістің кемшілігі мынада: ықтималдықтың таралу қисығынан жоғары
болып шыққан нүктелер қажетсіз деп танылып, оларды есептеуге кеткен
уақыт бекер болып шығады. Әдіс ықтималдықтың аналитикалық
функцияларына ғана қолданылады
.
Әдістің иллюстрациясы

6.

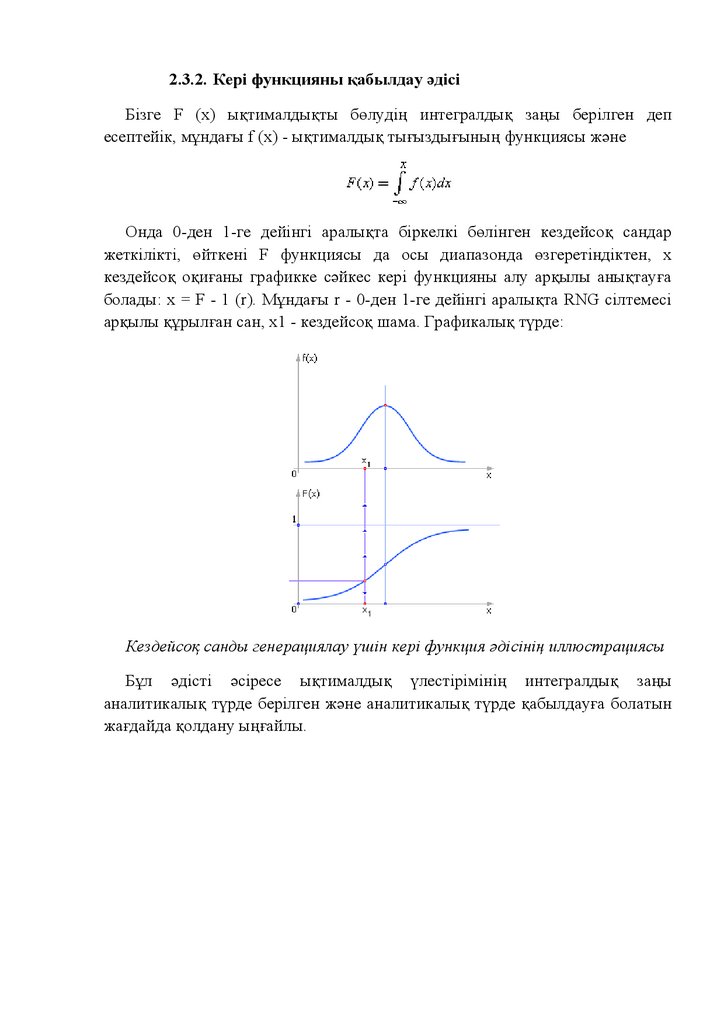
2.3.2. Кері функцияны қабылдау әдісі
Бізге F (x) ықтималдықты бөлудің интегралдық заңы берілген деп
есептейік, мұндағы f (x) - ықтималдық тығыздығының функциясы және
Онда 0-ден 1-ге дейінгі аралықта біркелкі бөлінген кездейсоқ сандар
жеткілікті, өйткені F функциясы да осы диапазонда өзгеретіндіктен, х
кездейсоқ оқиғаны графикке сәйкес кері функцияны алу арқылы анықтауға
болады: х = F - 1 (r). Мұндағы r - 0-ден 1-ге дейінгі аралықта RNG сілтемесі
арқылы құрылған сан, x1 - кездейсоқ шама. Графикалық түрде:
Кездейсоқ санды генерациялау үшін кері функция әдісінің иллюстрациясы
Бұл әдісті әсіресе ықтималдық үлестірімінің интегралдық заңы
аналитикалық түрде берілген және аналитикалық түрде қабылдауға болатын
жағдайда қолдану ыңғайлы.

7.

3. Қорытынды.
Сонымен берілген үлестірілген заңмен кездейсоқ сандарды модельдеу
аналитикалық мақсаттарда жиі қолданылады екен. Оны жүзеге асырудың
бірнеше тәсілдері бар: олардың ең негізгілері боп «Қадамды аппроксимация
әдісі» мен «Кері функцияны қабылдау әдісі» саналады. Сонымен қатар,
қысқарту әдісі де кездеседі.
Берілген үлестірілген заңмен кездейсоқ сандарды модельдеу формула
және график арқылы жүзеге асыруға болады.
Бүгінгі күнде модельдеуге арналған арнайы техникалар мен компьютерлік
бағдарламалар бар. Ол әр түрлі мақсатта қолданылады және әрқайсысы
өзіндік ерекшіліктері мен алгоритмдеріне ие.
Біз, логисттер үшін, кездейсоқ шамаларды берілген үлестірілген заңмен
модельдеу н/е өзге де түрлері өндірістік орындарда түрлі техникалық
проблемаларды шешуде, кейстерді ұйымдастыруда және шешуде
қолданылады.
Модельдеу сонымен қатар зерттеушіге эксперименттік ақпараттарды
береді.
4. Пайдаланылған әдебиеттер.
• http://stratum.ac.ru/ - Лекция 24
• МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ СЗАДАННЫМ
ЗАКОНОМ РАСПРЕДЕЛЕНИЯ – Учебный материал: электронная
версия.