Similar presentations:
Кездейсоқ шамалардың таңдамалы сипаттамалары. Жұптық сызықтық регрессия параметрлерін бағалау
1.
Кездейсоқ шамалардың таңдамалы сипаттамалары. Жұптық сызықтықрегрессия параметрлерін бағалау.
Осы тақырыпты ашып нақты статистикалық деректер негізінде талдау
жасаңыздар. (теория, формула, талдау көрсете білу).
Жоспар:
1. Кіріспе.
2. Теориялық аспект.
3. Талдау.
4. Қорытынды.
5. Пайдаланылған әдебиеттер.
1. Кіріспе.
1.1. Кездейсоқ шама.
2.
Кездейсоқ шама – жағдайға тәуелді белгілі бір ықтималдығы бар әртүрлі мән алатын қандай да бір шама.
Кездейсоқ шаманың түрлері - дискреттік және үзіліссіз. Егер кездейсоқ
шама нақты және есепті мән қабылдай алса, онда ол – дискреттік кездейсоқ
шама. Дискреттік кездейсоқ шаманы мынадай кестеде келтірсе болады:
x
x1
x2
...
xn
p
p1
p2
...
pn
Мұндағы, x1, x2, ... x – кездейсоқ шама қабылдай алатын барлық
мәндер жиынтығы; р1, р1, ... рn – мүмкін болатын ықтималдылықтар;
сәйкесінше:
Егер кездейсоқ шама мәнеді қандай да бір интервал аралығында
қабылдай алса, онда бұл шаманы үзіліссіз кездейсоқ шама дейміз.
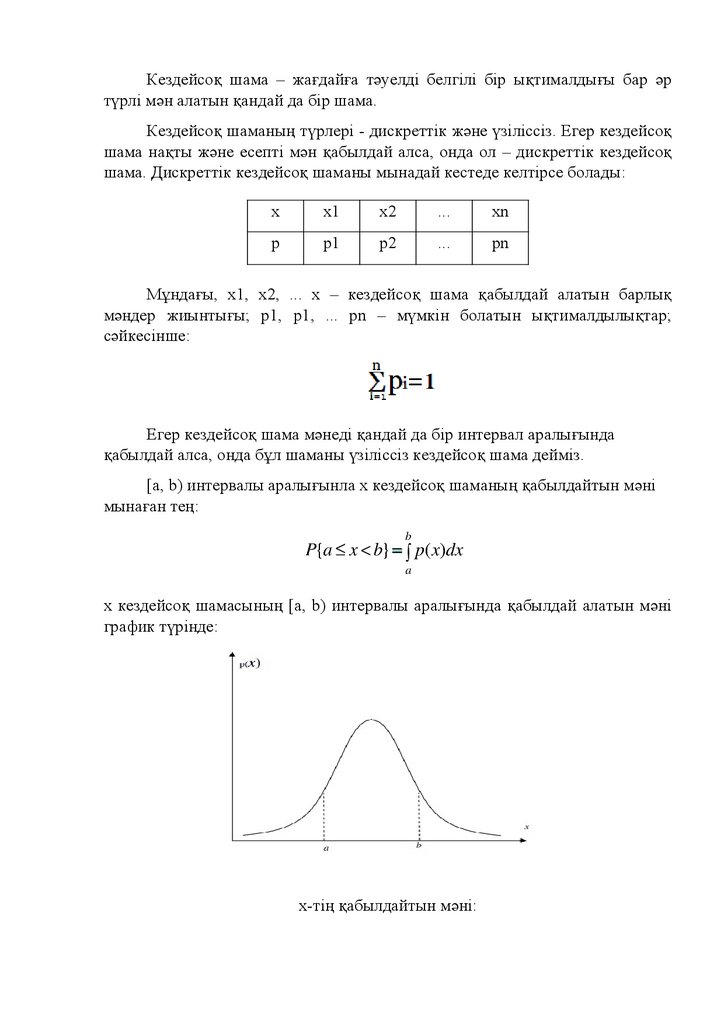
[a, b) интервалы аралығынла х кездейсоқ шаманың қабылдайтын мәні
мынаған тең:
х кездейсоқ шамасының [a, b) интервалы аралығында қабылдай алатын мәні
график түрінде:
х-тің қабылдайтын мәні:
3.
Математикалық күтім:- дискретті кездейсоқ шаманың мат.күтімі.
- үзіліссіз кездейсоқ шаманы мат.күтімі.
1.2. Жұптық сызықтық регрессия.
Жұптық сызықтық регрессия дегеніміз – бірайнымалы мәннің екінші
бір айнымалы мән арасындағы байланыс.
Формуласы: y=ax+b+e;
Мұндағы:
y - нәтижелі белгінің түзетілген мәндері (тәуелді айнымалы),
x- факторлы белгінің мәндері (тәуелсіз айнымалы),
b-тәуелді айнымалының орташа өзгертілуін көрсететін регрессия
коэффициенті.
е – кездейсоқ мүше.
Регрессия теңдеуінің көмегімен көрсеткіштің тегістелген мәндерін
және ауытқуларын есептеуге болады. Ауытқулардың қосындысы әрқашан
нөлге тең.
Белгілер арасындағы мөлшерлі тәуелділіктердің орнықтылығы әр
түрлі экономикалық зерттеулер үшін маңызды мән атқарады.
Ең кіші квадраттар әдісі - ықтималдылықтар теориясының белгісіз
шамаларды кездейсоқ қателері бар өлшеулердің нәтижесін бағалау үшін
қолданатын әдістерінің бірі. Ең кіші квадраттар әдісі берілген функцияларды
олардан гөрі қарапайым функциялар арқылы жуықтап өрнектеу үшін де
пайдаланылады.
4.
Ең кіші квадраттар методы арқылы жұптық сызықтар параметрлерінбағалау үшін төмендегі шарттар орындалуы тиіс:
- Зерттейтін процесстің мақсаты толық тұжырымдалады; - ең неізгі
сапалық мінездемелері факторлары анықталады;
- функционалдық, структуралық, құраушы элементтері анықталады; элементтерінің арасындағы байланыстарға сөзбен сапалық саралау мен
сипаттау жасалады;
- дәл, қысқа, компакты түрде математикалық модель құрастырылады; модельдің шешімі алынып, жан-жақты анализ (адекваттығынан бастап,
қорытындысы арқылы болжам) жасалады.
Мұндай жағдайда, “шығынының” орташа мәні ең кіші болатындай Х
шамасының жүйелі қатесін тиімді баға деп есептеуге болады. Міне, осы
талап Ең кіші квадраттар әдісінің негізіне алынады. Ал, жалпы жағдайда, Х
шамасының Ең кіші квадраттар әдісі мағынасындағы тиімді бағасын іздеу
күрделі есеп.
2. Теориялық аспект.
2.1. Таңдамалы сипаттамалары.
• Таңдамалы орташа:
• х айнымалының таңдамалы вариациясы:
• х кездейсоқ шаманың таңдамалы дисперсиясы:
• Таңдамалы стандартты ауытқу:
5.
• Таңдамалы ковариация:• Формула дұрыстығын тексеру:
• Var(x) - Cov(x,х) тең болады:
• Корреляцияның таңдамалы коэффициенті:
2.2. Жұптық сызықтық регрессия параметрлерін бағалау.
Жұптық сызықтық регрессия параметрлерін
қолданылатын метод – ең кіші квадраттар методы.
бағалауда
ең жиі
Ең кіші квадраттар методының міндеті – шыққан мәннің yi есепті
мәннен
ауытқуының квадратының соммасы минималды болатын
бағалау параметрлерін алу.
,
Бұл критерий мына формула арқылы түсіндірсек болады: ▼
Ең кіші квадраттар әдісінің мәні — физикалық шаманың дәл мәнін
(белгісіз) оның бақылаулар нәтижесінде есептелген жуық мәнімен (Х)
ауыстырғандағы ең кіші қателік квадратына пропорционал болады деген
пайымдауға негізделген.
Ең кіші квадраттар әдісінің мәнін график арқылы сипаттасақ:▼
6.
Математикалық сипаты▼:Мұндағы, yi және xi=1...n мәндері бізге белгілі – оны бақылау арқылы
аламыз; және бағалау параметрлері айнымалы боп табылады. Аталған 2
айнымалының мәндерін табу үшін олардың ішінара туындыларын нөлге
теңестіріп аламыз:
Нәтижесінде сызықтық теңдеулер жүйесін аламыз:
Осы жүйені шеше отырып,
параметрлерінің бағаларын табамыз:
3. Талдау.
жұптық
сызықтық
регрессия
7.
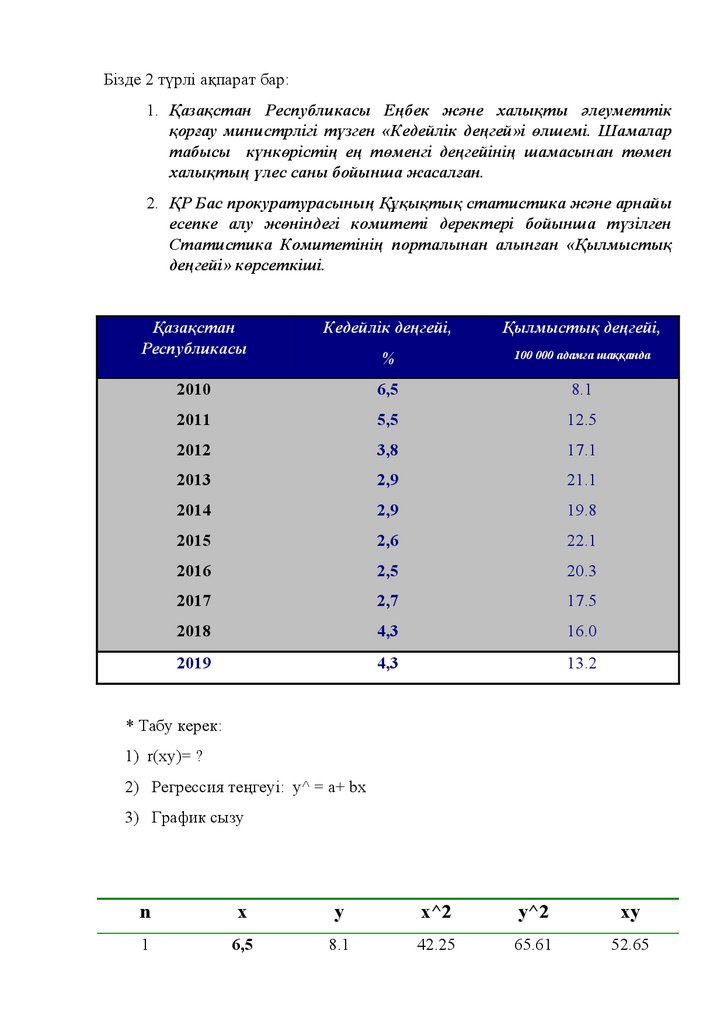
Бізде 2 түрлі ақпарат бар:1. Қазақстан Республикасы Еңбек және халықты әлеуметтік
қорғау министрлігі түзген «Кедейлік деңгей»і өлшемі. Шамалар
табысы күнкөрістің ең төменгі деңгейінің шамасынан төмен
халықтың үлес саны бойынша жасалған.
2. ҚР Бас прокуратурасының Құқықтық статистика және арнайы
есепке алу жөніндегі комитеті деректері бойынша түзілген
Статистика Комитетінің порталынан алынған «Қылмыстық
деңгейі» көрсеткіші.
Қазақстан
Республикасы
Кедейлік деңгейі,
Қылмыстық деңгейі,
%
100 000 адамға шаққанда
2010
6,5
8.1
2011
5,5
12.5
2012
3,8
17.1
2013
2,9
21.1
2014
2,9
19.8
2015
2,6
22.1
2016
2,5
20.3
2017
2,7
17.5
2018
4,3
16.0
2019
4,3
13.2
* Табу керек:
1) r(xy)= ?
2) Регрессия теңгеуі: y^ = a+ bx
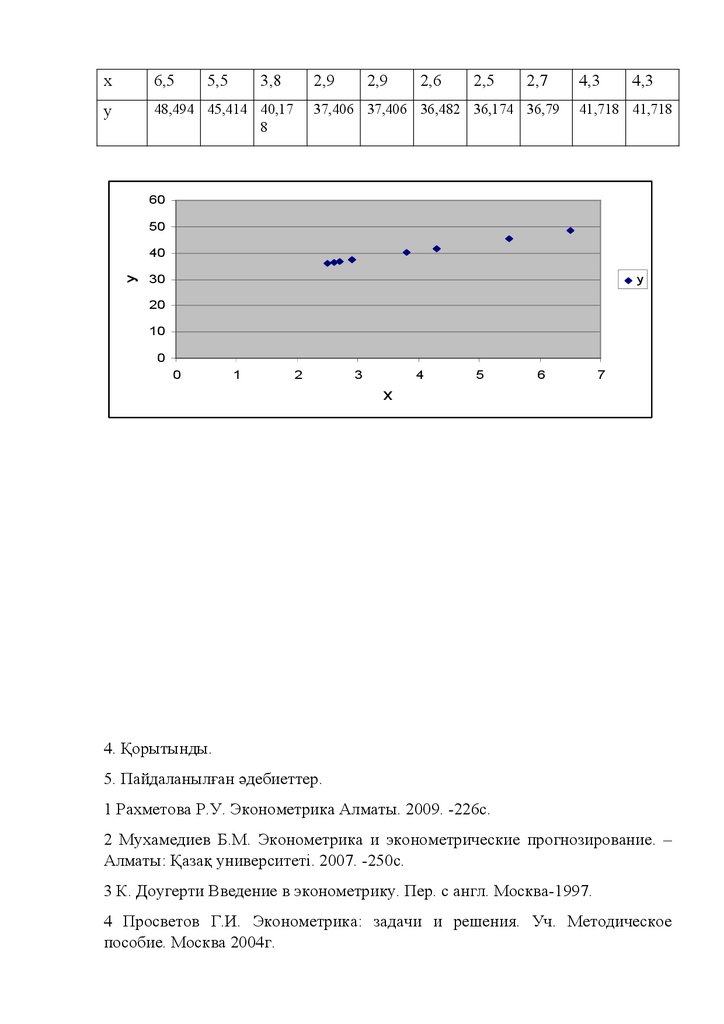
3) График сызу
n
x
y
x^2
y^2
xy
1
6,5
8.1
42.25
65.61
52.65
8.
25,5
12.5
30.25
156.25
68.75
3
3,8
17.1
14.44
292.41
64.98
4
2,9
21.1
8.41
445.21
61.19
5
2,9
19.8
8.41
392.04
57.42
6
2,6
22.1
6.76
488.41
57.46
7
2,5
20.3
6.25
412.09
50.75
8
2,7
17.5
7.29
306.25
47.25
9
4,3
16.0
18.49
256.00
68.8
10
4,3
13.2
18.49
174.24
56.76
E
38
167.7
161.04
2988.51
586.01
E/n
3.8
16.77
16.104
298.851
58.601
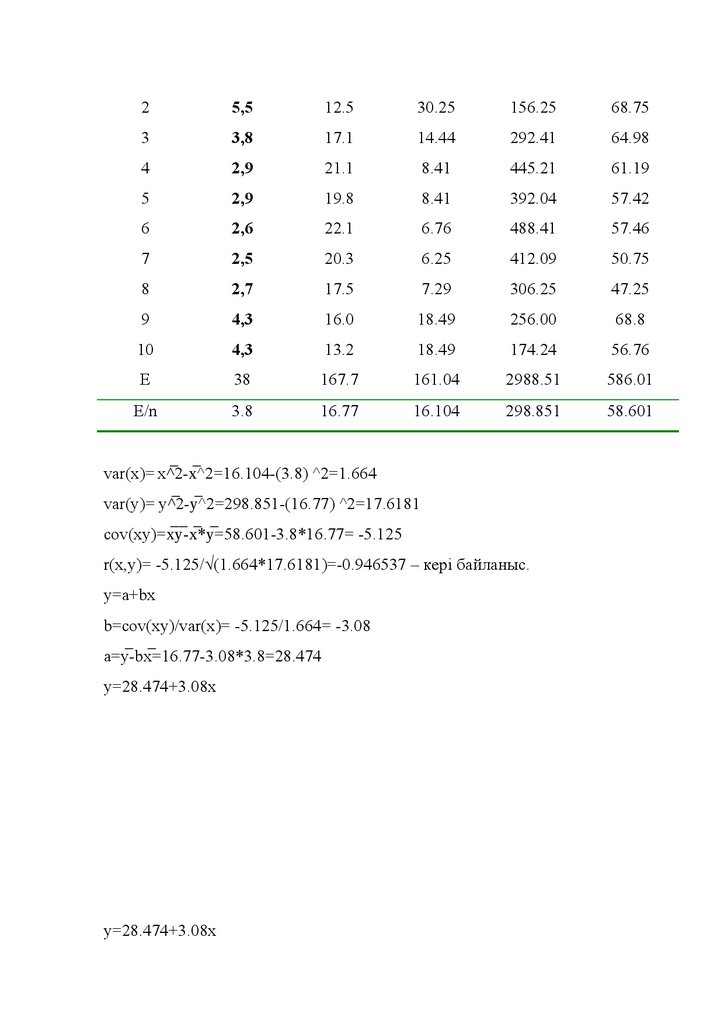
var(x)= x^̅2-x̅^2=16.104-(3.8) ^2=1.664
var(y)= y^̅2-y̅^2=298.851-(16.77) ^2=17.6181
cov(xy)=x̅y-̅ x̅*y̅=58.601-3.8*16.77= -5.125
r(x,y)= -5.125/√(1.664*17.6181)=-0.946537 – кері байланыс.
y=a+bx
b=cov(xy)/var(x)= -5.125/1.664= -3.08
a=y-̅ bx=16.77
̅
-3.08*3.8=28.474
y=28.474+3.08x
y=28.474+3.08x
9.
x6,5
5,5
3,8
y
48,494 45,414 40,17
8
2,9
2,9
2,6
2,5
2,7
37,406 37,406 36,482 36,174 36,79
4,3
4,3
41,718 41,718
60
50
У
40
30
y
20
10
0
0
1
2
3
4
5
6
7
Х
4. Қорытынды.
5. Пайдаланылған әдебиеттер.
1 Рахметова Р.У. Эконометрика Алматы. 2009. -226с.
2 Мухамедиев Б.М. Эконометрика и эконометрические прогнозирование. –
Алматы: Қазақ университеті. 2007. -250с.
3 К. Доугерти Введение в эконометрику. Пер. с англ. Москва-1997.
4 Просветов Г.И. Эконометрика: задачи и решения. Уч. Методическое
пособие. Москва 2004г.
10.
5 Брейли Р. Принципы корпоративных финансов: Пер. с англ.-М.:ЗАО«Олимп-Бизнес», 1997
6 Ә.Ж. Сапарбаев, А.Т. Мақұлова. Эконометрика. Алматы: Бастау, 2007ж.
7 Бухвалов А.В. Самоучитель по финансовым расчетам.- М.: Мир,Пресссервис, 1997
8 Қаржы-экономика сөздігі. - Алматы: ҚР Білім және ғылым министрлігінің
Экономика институты, "Зияткер" ЖШС, 2007
9 Елисеева И.И Эконометрика. –М.: Финансы и статистика, 2005. -576с.
10 www.wikipedia.kz






 mathematics
mathematics








