Корреляция теориясының элементтері

1. Корреляция теориясының элементтері аға оқытушы Раманқұлова А.А.

2. Жоспар:

Статистикалық және корреляциялық
байланыстар.
Сызықты регрессия теңдеуі.
Регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Корреляция коэффициенті,оның
мағынасы және қасиеттері.
Спирменнің рангілік корреляция
коэффициенті.

3. Статистикалық тәуелділік

Анықтама 1. Егер бір кездейсоқ шаманың
өзгеруіне екінші кездейсоқ шаманың таралу
заңының өзгеруі сәйкес келсе, онда олардың
арасындағы тәуелділік статистикалық деп
аталады.
Анықтама 2. Егер бір кездейсоқ шаманың
өзгеруіне екінші кездейсоқ шаманың орта
мәнінің өзгеруі сәйкес келсе, онда олардың
арасындағы статистикалық тәуелділік
корреляциялық деп аталады.

4.

Корреляциялық өріс

5. Тәуелділіктер түрлері:

Функционалдық
y f (x)
Корреляциялық
yx f ( x )

6. Регрессияның таңдама теңдеуі:

У тің Х
yx f ( x )
Х тің У
xy y

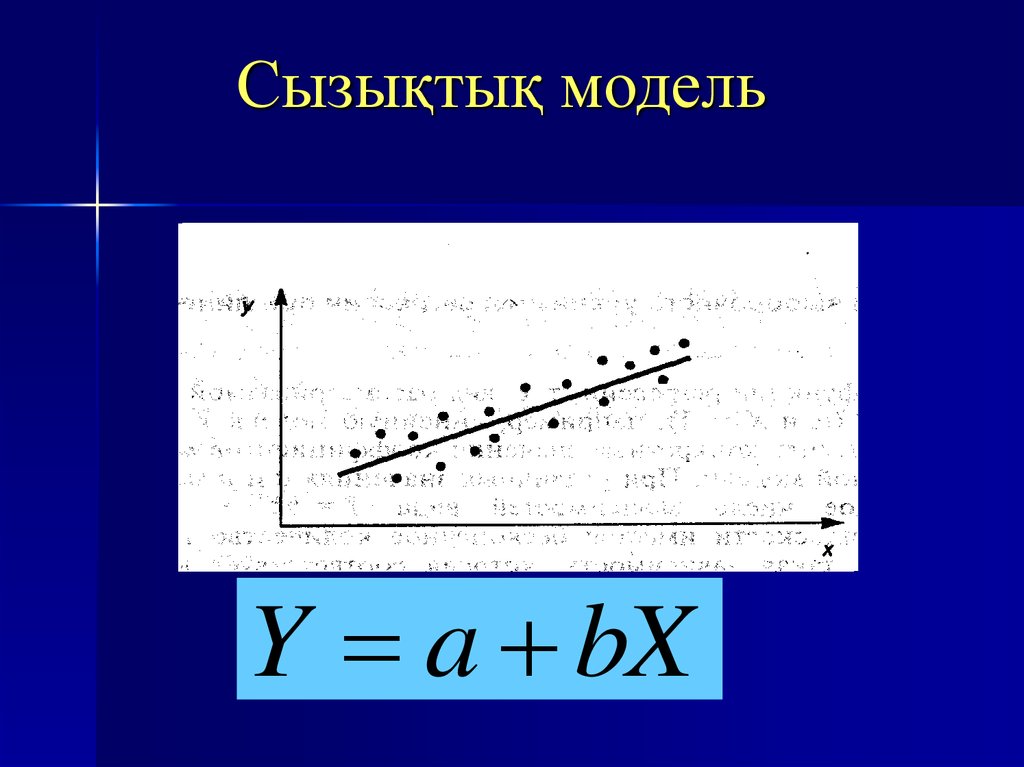
7.

Сызықтық модель
Y a bX

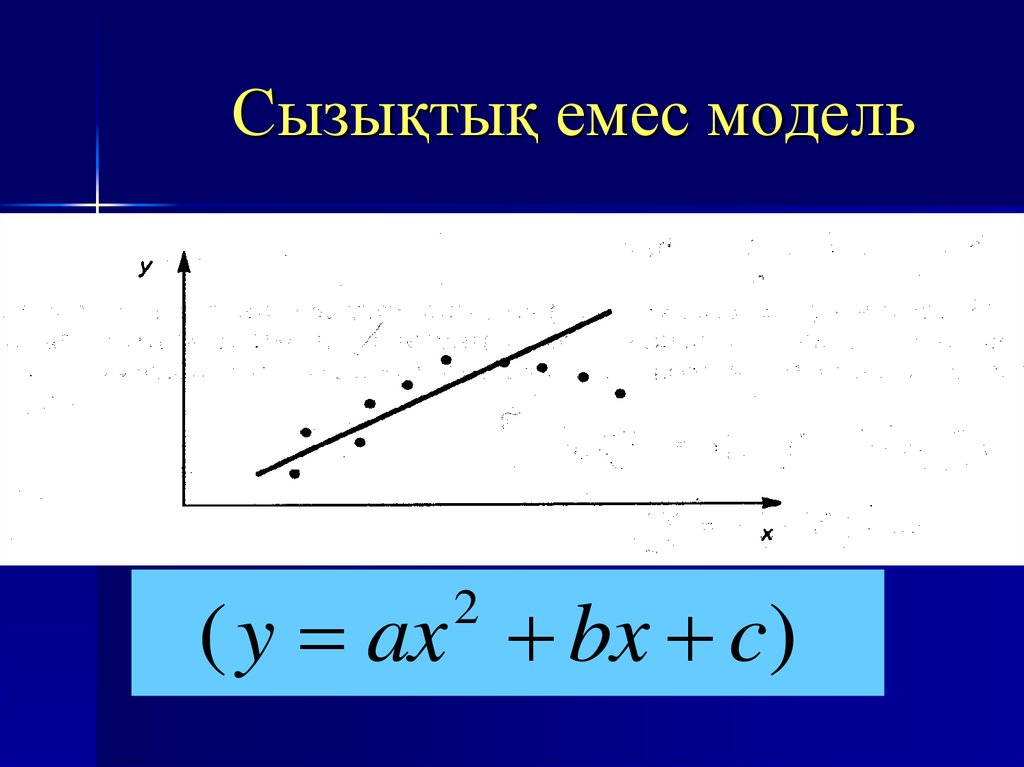
8. Сызықтық емес модель

( y ax bx c)
2

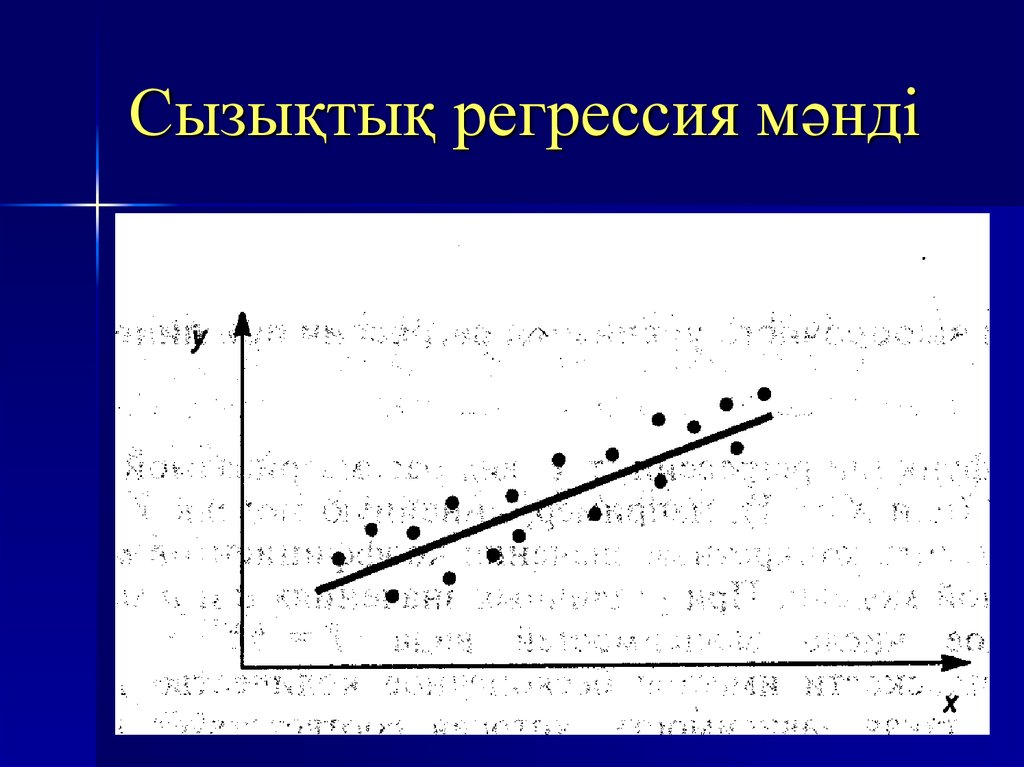
9. Сызықтық регрессия мәнді

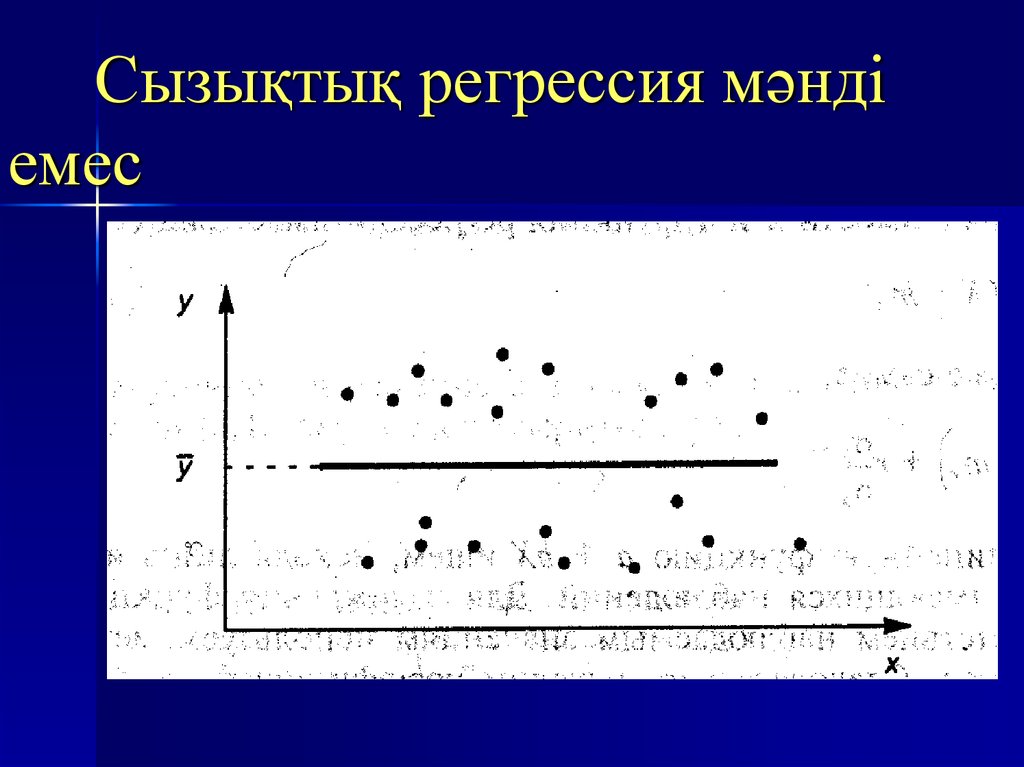
10. Сызықтық регрессия мәнді емес

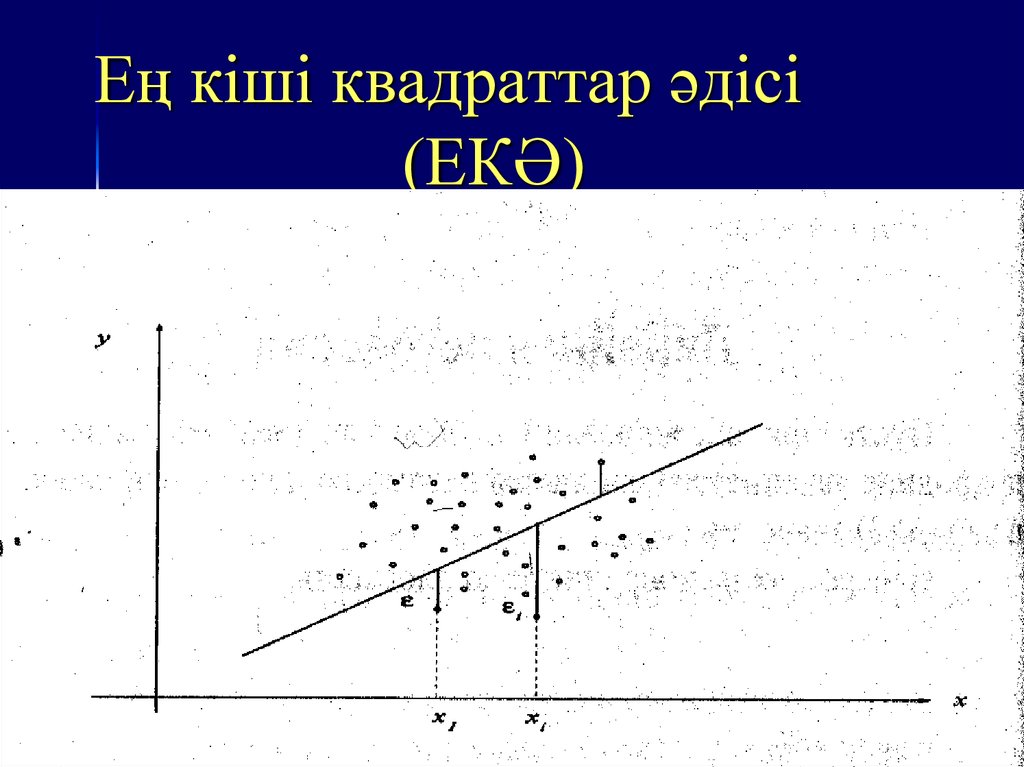
11. Ең кіші квадраттар әдісі (ЕКӘ)

12.

Y a bх
( х x)( y y )
b
(
x
x
)
i
i
2
- регрессия
коэффициенті
i
a y bx
- бос мүше

13. Теориялық сызықтық регрессия сызығын бағалау.

Y y b( x x )
У тің Х ке сызықтық
регрессиясының таңдама теңдеуі

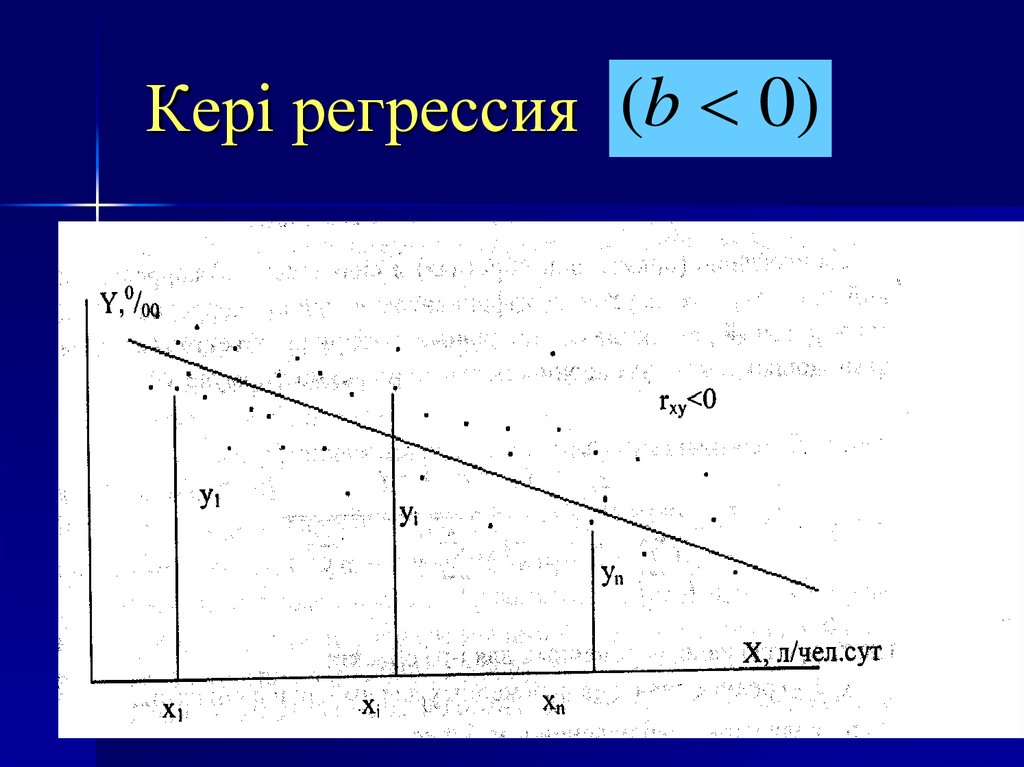
14. Кері регрессия

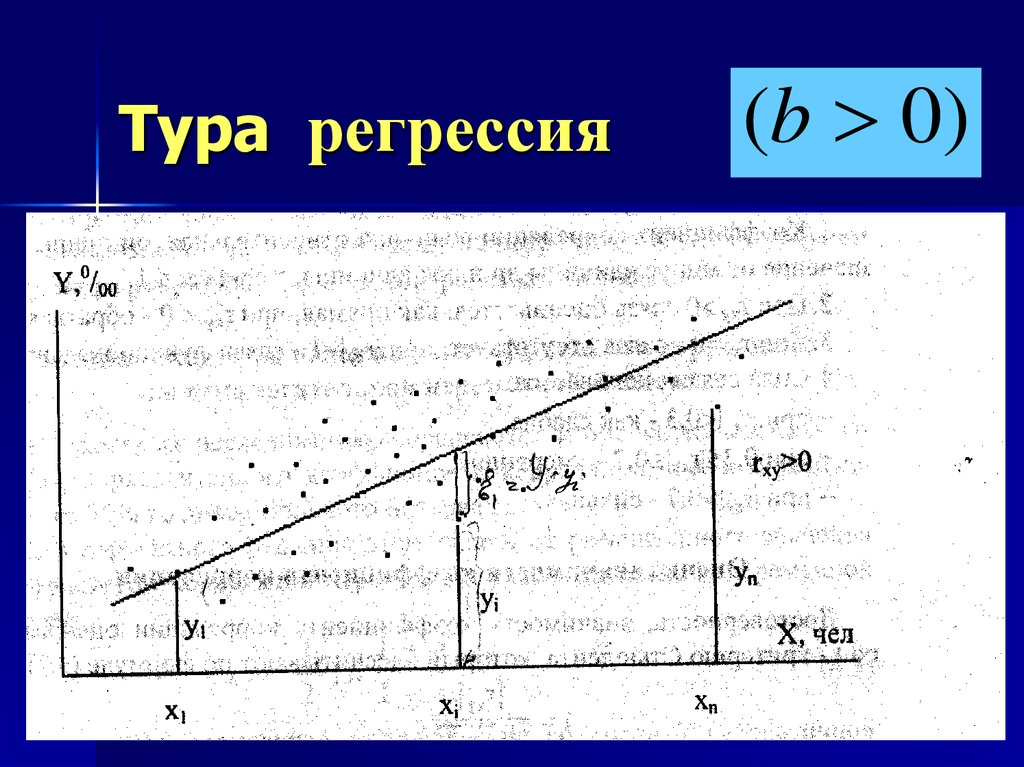
(b 0)

15. Тура регрессия

(b 0)

16. Регрессия коэффициентінің мәнділігі жөніндегі жорамалды тексеру :

жорамалдарын анықтаймыз :
1. H0 және H1
H0: b=0 (шамалар арасында сызықтық
тәуелділік жоқ),
H1: b≠0.
2. α мәнділік деңгейін береміз.

17.

3. Критерий статистикасын есептейміз
n
b
F
2
(x
i
i 1
s
x)
2
2
n
s
2
(y
i 1
i
y)
2
n 2
F статистикасы 1 және (n-2) еркіндік
дәрежесімен Фишердің таралуы.

18.

Fбақылау және Fα,1,n-2 сындық
нүктелерін анықтау.
4.
5. Егер │ F│>Fα,1,n-2 , онда H0 жоққа
шығарылады.
Егер │F│<Fα,1,n-2 , онда H0 қабылданады.

19. Детерминация коэффициенті :

Х-тің У-ке
Х a ху bху у
У-тің Х-ке
У a ух b ух х
R bух bxy
2

20. Регрессиялық талдау міндеттері:

Регрессия коэффициенті мен бос
мүшені бағалау;
Регрессия теңдеуін анықтау және
жіберілетін қателікті бағалау.
Регрессияның мәнділігі жөніндегі
жорамалды тексеру.
Модельдің адекваттық (барабарлық)
дәрежесін бағалау.

21. Корреляциялық талдаудың міндеттері:

Корреляцияның
таңдама
коэффициентін есептеу.
Корреляциялық кесте құру.
Корреляциялық байланыстың
мәнділігінің статистикалық жорамалын
тексеру.

22. Сызықтық корреляцияның таңдама коэффициенті

n
rТ
(
x
x
)(
y
y
)
i i
i 1
n
n
( x x) ( y y )
2
i 1
i
i 1
i
2

23.

Корреляцияның таңдама
коэффициентінің негізгі мағынасы–
сәйкес сызықтық корреляцияның бас
коэффициентін эмпирикалық бағалау.

24. Сызықтық регрессияның таңдама теңдеуі

У тіңХ
Х тің У
Y
Y Y rТ
(X X )
X
X
X X rТ
(Y Y )
Y

25. Корреляция коэффициентінің негізгі қасиеттері :

1. r = 0 – байланыс жоқ,
2. r>0 – тура байланыс,
r <0 – кері байланыс,
3.
r 1
4. r = 1 - толық байланыс.

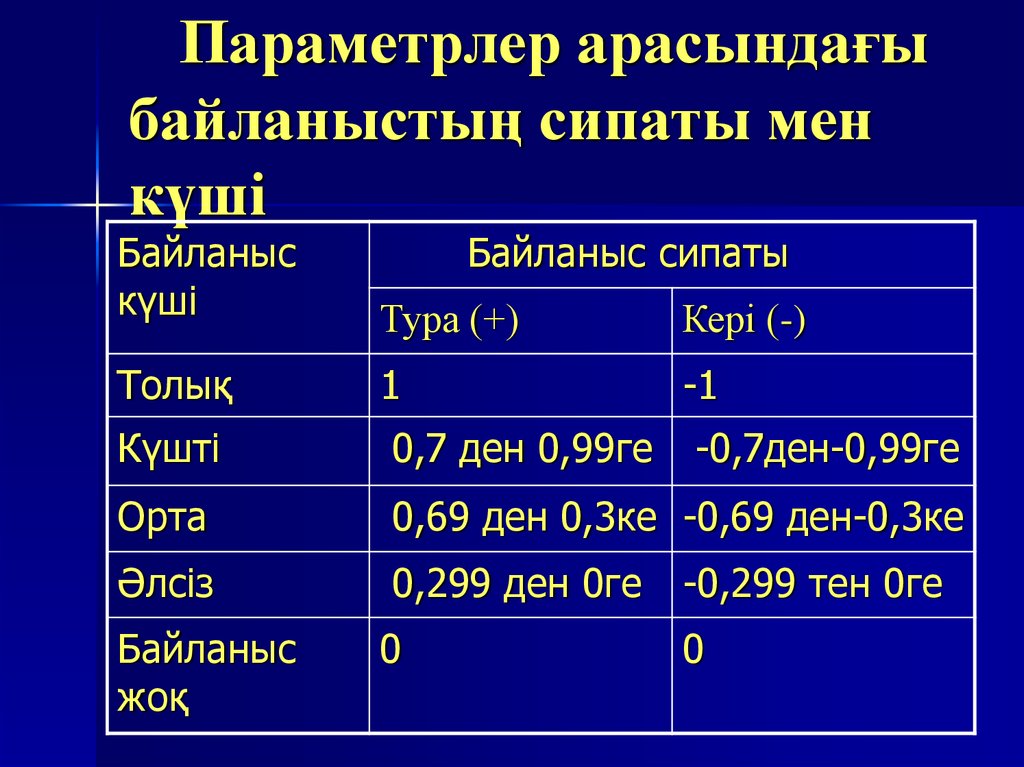
26. Параметрлер арасындағы байланыстың сипаты мен күші

Байланыс
күші
Байланыс сипаты
Тура (+)
Кері (-)
Толық
1
-1
Күшті
0,7 ден 0,99ге
Орта
0,69 ден 0,3ке -0,69 ден-0,3ке
Әлсіз
0,299 ден 0ге
Байланыс
жоқ
0
-0,7ден-0,99ге
-0,299 тен 0ге
0

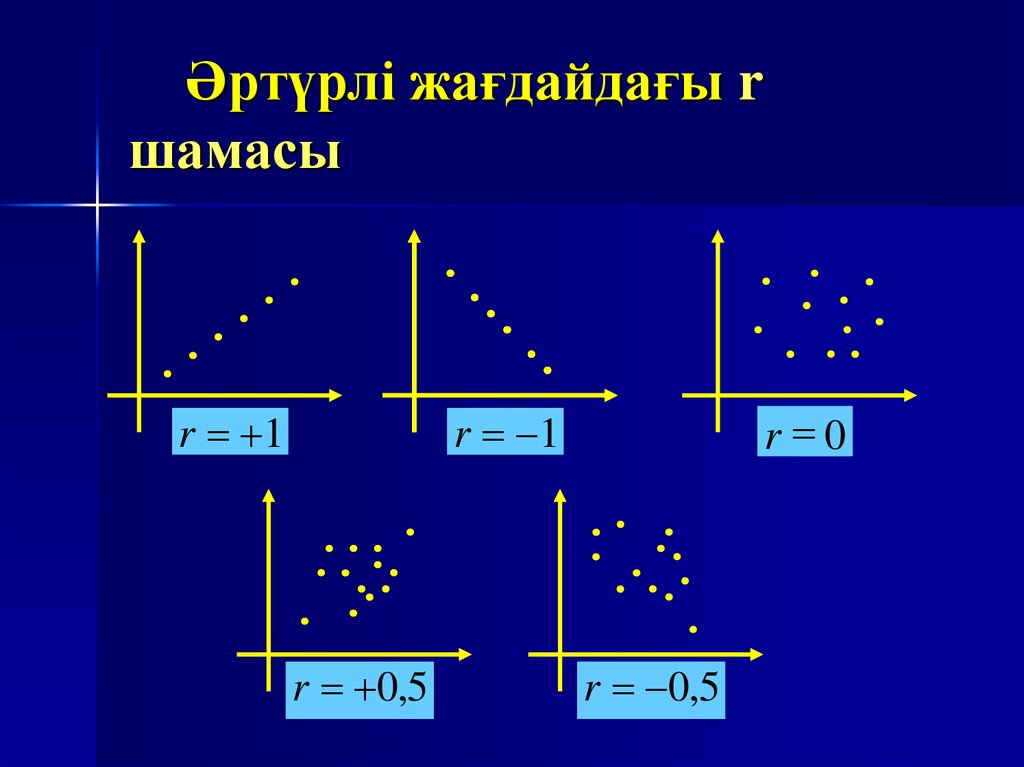
27. Әртүрлі жағдайдағы r шамасы

r 1
r 0
r 1
r 0,5
r 0,5

28. Корреляция коэффициентінің есептелмейтін жағдайлары:

29. Корреляция коэффициентінің мәнділігі жөніндегі жорамалды тексеру :

1. H0 және H1 жорамалдарын
анықтаймыз :
H0: r=0 (корреляция жоқ),
H1: r ≠0.
2. α мәнділік деңгейін береміз,

30.

3. Критерий статистикасын есептейміз:
t
r
1 r
2
n 2
t статистикасы еркіндік дәрежесі (n-2) ге
тең болатын Стьюдент таралуы.

31.

4. tбақылау және
tα,n-2 сындық
нүктелерін табамыз.
5. Егер │t│ ≥ tα,n-2 , онда H0 жоққа
шығарылады.
Егер │t│ < tα,n-2 , онда H0
қабылданады.

32. Әдебиеттер.

С.А.Нұрпейісов, О.С.Сатыбалдиев,
М.Өтепбергенұлы. Ықтималдықтар теориясы және
математикалық статистика,Оқу
құралы,Алматы,Экономика,2005.
И.В. Павлушков и др. Основы высшей математики и
математической статистики, М., Издательский дом
ГЭОТАР-МЕД, 2003г.
Е.А. Лукьянова “Математическая статистика”-М.,
РУДН, 2002г
В.И. Юнкеров, С.Г. Григорьев “Математикостатистическая обработка данных медицинских
исследований” С.-П.,2002г

33. НАЗАРЛАРЫҢЫЗҒА РАХМЕТ