Similar presentations:
Экономикадағы статистикалық байланыстар
1.
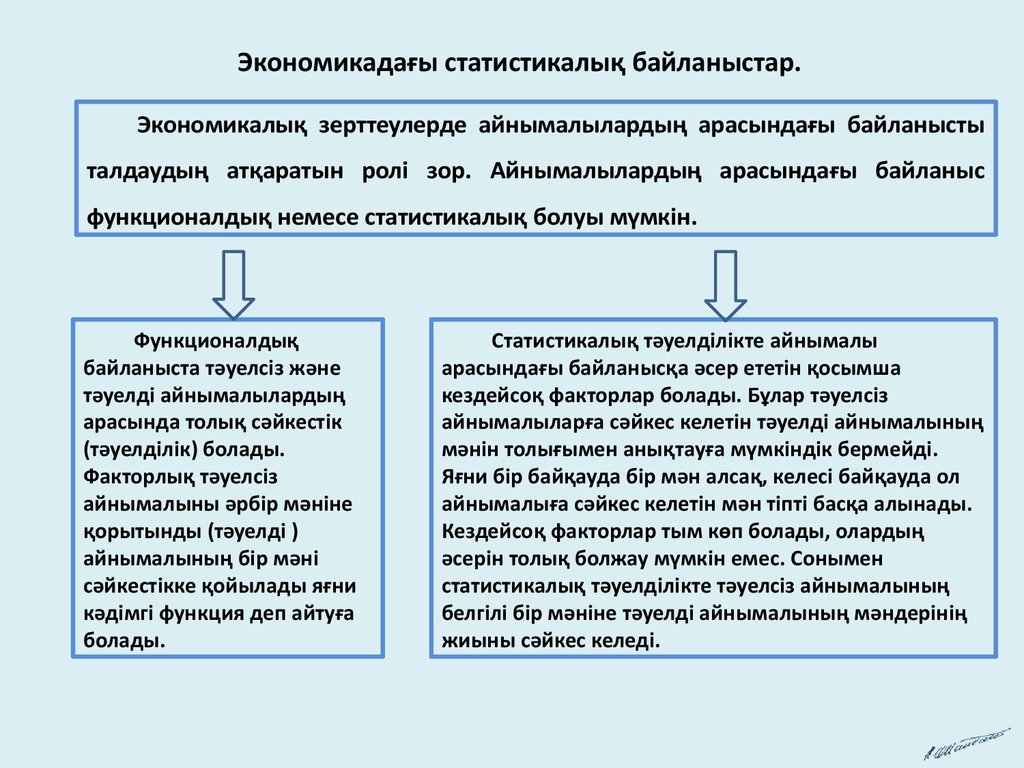
Экономикадағы статистикалық байланыстар.Экономикалық зерттеулерде айнымалылардың арасындағы байланысты
талдаудың атқаратын ролі зор. Айнымалылардың арасындағы байланыс
функционалдық немесе статистикалық болуы мүмкін.
Функционалдық
байланыста тәуелсіз және
тәуелді айнымалылардың
арасында толық сәйкестік
(тәуелділік) болады.
Факторлық тәуелсіз
айнымалыны әрбір мәніне
қорытынды (тәуелді )
айнымалының бір мәні
сәйкестікке қойылады яғни
кәдімгі функция деп айтуға
болады.
Статистикалық тәуелділікте айнымалы
арасындағы байланысқа әсер ететін қосымша
кездейсоқ факторлар болады. Бұлар тәуелсіз
айнымалыларға сәйкес келетін тәуелді айнымалының
мәнін толығымен анықтауға мүмкіндік бермейді.
Яғни бір байқауда бір мән алсақ, келесі байқауда ол
айнымалыға сәйкес келетін мән тіпті басқа алынады.
Кездейсоқ факторлар тым көп болады, олардың
әсерін толық болжау мүмкін емес. Сонымен
статистикалық тәуелділікте тәуелсіз айнымалының
белгілі бір мәніне тәуелді айнымалының мәндерінің
жиыны сәйкес келеді.
2.
Ковариация дегеніміз екі айнымалының арасындағыбайланысты (тәуелділікті) көрсететін статистикалық өлшем, басқаша
айтқанда, екі айнымалының арасындағы сызықтық байланыстың
(тәуелділіктің) мөлшері
X
x1
x2
…
xn
Y
y1
y2
…
y2
1 n
x1 x2 ... xn
x xi
n i 1
n
1 n
xi x yi y
cov( X , Y )
n 1 i 1
1 n
cov( X , Y ) xi x yi y
n i 1
1 n
y1 y2 ... yn
y yi
n i 1
n
таңдама жиын үшін
бас жиын үшін
3.
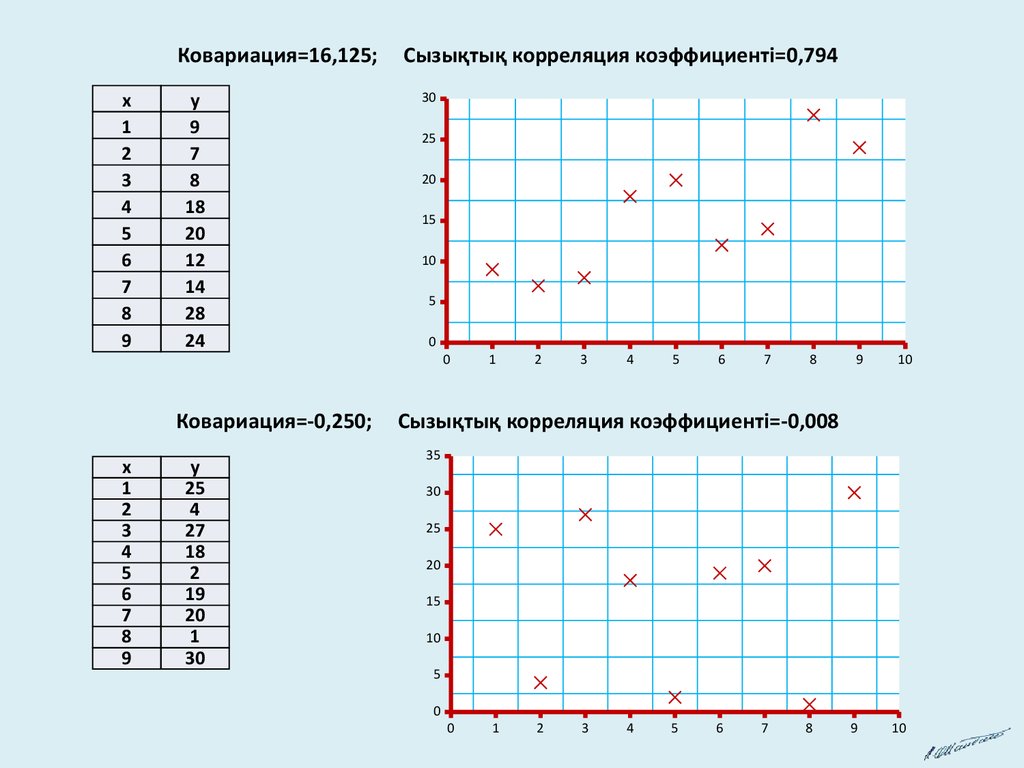
Ковариация=16,125;x
1
2
3
4
5
6
7
8
9
y
9
7
8
18
20
12
14
28
24
Сызықтық корреляция коэффициенті=0,794
30
25
20
15
10
5
0
0
Ковариация=-0,250;
x
1
2
3
4
5
6
7
8
9
y
25
4
27
18
2
19
20
1
30
1
2
3
4
5
6
7
8
9
10
Сызықтық корреляция коэффициенті=-0,008
35
30
25
20
15
10
5
0
0
1
2
3
4
5
6
7
8
9
10
4.
Ескерту. EXCEL-де ковариация есептеуге арналған екі функция барКОВАРИАЦИЯ.В (таңдама жиынтыққа - выборкаға), КОВАРИАЦИЯ.Г (бас
жиынтыққа - генеральное совокупность ) арналған.
Ковариацияның қасиеттері
орта квадраттық ауытқулар.
5.
Егер Х,У бір бірінен тәуелсіз болатын болса олардың арасындағытеориялық ковариация нольге тең болады. Ковариацияның шамасы
Х пен У өлшенген өлшем бірліктеріне тәуелді яғни басқа өлшем
бірліктеріне көшсе ковариацияның шамасы өзгереді.
Егер ковариация оң сан болса, айнымалылардың бірі өскенде
екіншісі де өседі, ал теріс сан болса, айнымалылардың бірі өскенде
екіншісі кемиді.
Ковариацияның шамасына қарап айнымалылардың арасындағы
тығыздық мөлшерін анықтай алмаймыз (себебі ковариацияның
шамасы айнымалылар өлшеніп отырған өлшем бірлігіне тәуелді).
6.
Ковариация айнымалылардың арасында байланыс бар жо ғын ғанакөрсетеді. Ковариация шамасына қарап олардың арасында ғы байланыс
қаншалықты тығыз екенін айта алмаймыз. Сондықтан іс ж үзінде осы
тығыздық шамасын сипаттау үшін сызықтық корреляция коэффициенті,
немесе Пирсонның корреляция коэффициенті деген шама енгізеді.
Бас жиынның сызықтық корреляция коэффициенті (оны теориялы қ
корреляция коэффициенті деп атайды) мына формуламен аны қталады
( , )
=
=
∗
√
мұнда
√
√
´
´
=
( − ) , =
( − )
∑
∑
=
=
7.
Корреляция коэффициенті екі айнымалының арасындағы сызықтық
тәуелділіктің қаншалық тығыз екенін көрсетеді.
Егер болса, Х,У кездейсоқ шамаларының арасында өте тығыз
байланыс бар болғаны. Егер
болса, Х,У кездейсоқ шамаларының арасында
сызықтық байланыс жоқ болғаны. Сызықтық байланыс жоқ деген сөз
олардың арасында тіпті байланыс жоқ деген сөз емес. Олардың арасында
сызықтық емес байланыс болуы да мүмкін.
Іс жүзінде бас жиынтықтың корреляция коэффициенті белгісіз. Таңдама
жиынды зерттеу арқылы сол ρ корреляция коэффициентінің нүктелік
баламасын ғана табамыз. Сол нүктелік баламаны әрпімен белгілейік.
коэффициенті кездейсоқ шама, ал ρ кездейсоқ шама емес.
8.
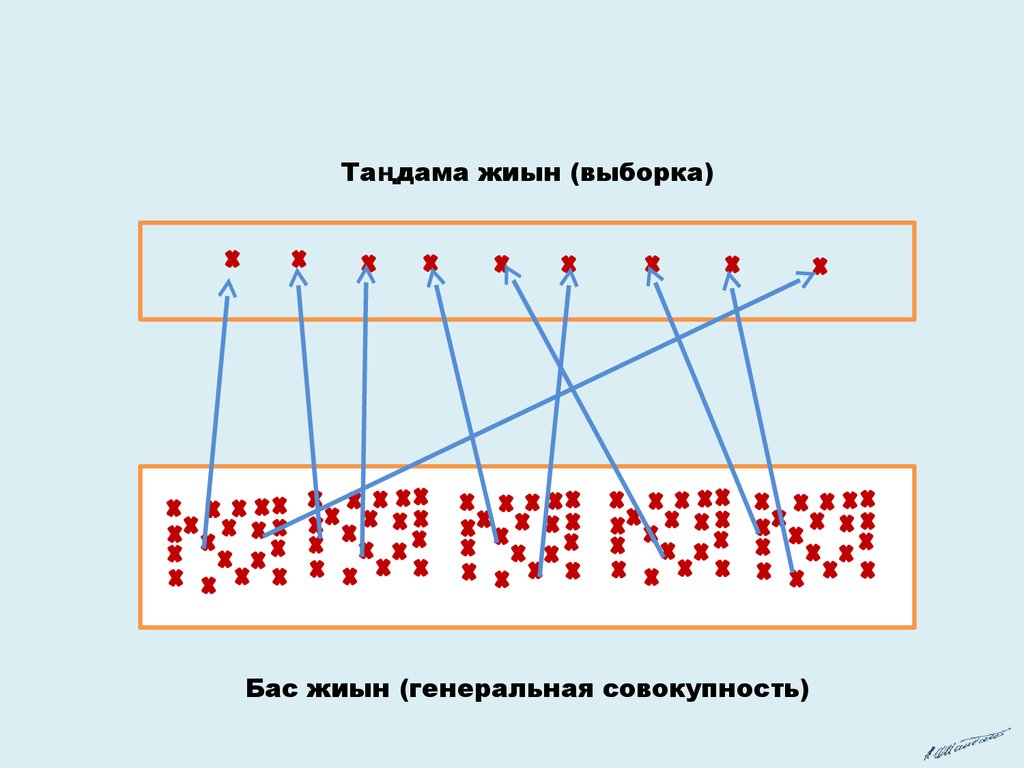
Таңдама жиын (выборка)Бас жиын (генеральная совокупность)
9.
Таңдамакорреляция
жиынның
корреляция
коэффициентінің
коэффициенті
нүктелік
баламасы)
(теориялық
төмендегі
формуламен анықталады.
n
1
xi x yi y
n 1 i 1
r xy
SxS y
n
x
i 1
n
i
x yi y
n
2
x
x
y
y
i
i
i 1
2
i 1
Мұнда Sx, Sy шамалары {xi}, {yi} айнымалыларының олардың
арифметикалық орта мәндерінен қаншалықты бытыра ңқы (шашыра ңқы)
орналасатынын көрсететін дисперсиялар, олар төмендегі формулалармен
анықталады
´
´
х=
( − ) , =
( − )
∑
∑
− =
− =
10.
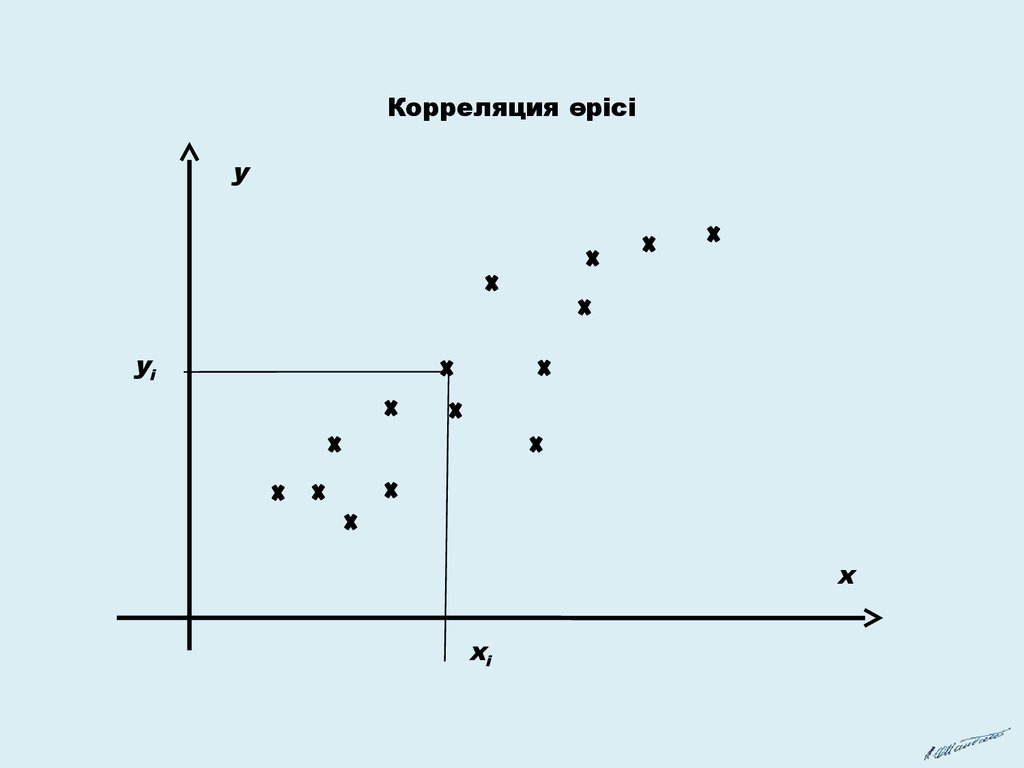
Корреляция өрісіy
yi
x
xi
11.
Корреляция коэффициентін тек қана екі айнымалы емес көптегенайнымалылар үшін де есептеуге болады. Егер біз бірнеше Y, X 1, X2, …, Xn
айнымалыларын қарастырсақ, онда төмендегі матрица жұптық
корреляция коэффициенттерінің матрицасы деп аталады.
1
ryx1
R ryx2
...
r
yxn
ryx1
1
r x1 x2
...
rx1 xn
ryx 2
rx1 x2
1
...
rx2 xn
... ryxn
... rx1xn
... rx2 xn
... ...
...
1
12.
Спорттан командалық кездесулер өтетін, әртүрлі концерттер немесе басқаойын-сауық шаралары өтетін жабық стадион менеджерлерінің алдында
тұратын мынандай проблеманы қаралық. Менеджерлер әрбір осындай
шаралар кезінде стадионға қанша адам жиналатынын білуге тырысады, соған
қарап әртүрлі ұйымдастыру жұмыстарын жүргізіп қорымен көрсететін
ұжымдармен де келіссөз жүргізіп біраз шаралар қабылдауы керек. Алдыңғы
жағдайлаоды зерттей келіп стадион жиналатын адамдар саны мен бір күн
бұрын салынған билеттер санының арасында байланыс бар болса, онда бір күн
бұрынғы сатылған билеттердің саны белгілі болғандықтан соңғы күнді
адамдар санына қарап жобалап ұйымдастыру жұмыстарын жүргізуге болады.
Соңғы бес шарадан мынандай мәлеметтер жиналған
Бір күн бұрын сатылған билет саны (мың)
Қатысқан адамдар саны (мың)
3,5
8,1
4,6
9,4
5,8
11,3
4,2
6,9
5,2
9,7
13.
1211
10
9
8
7
6
3
3,5
4
4,5
5
5,5
6
14.
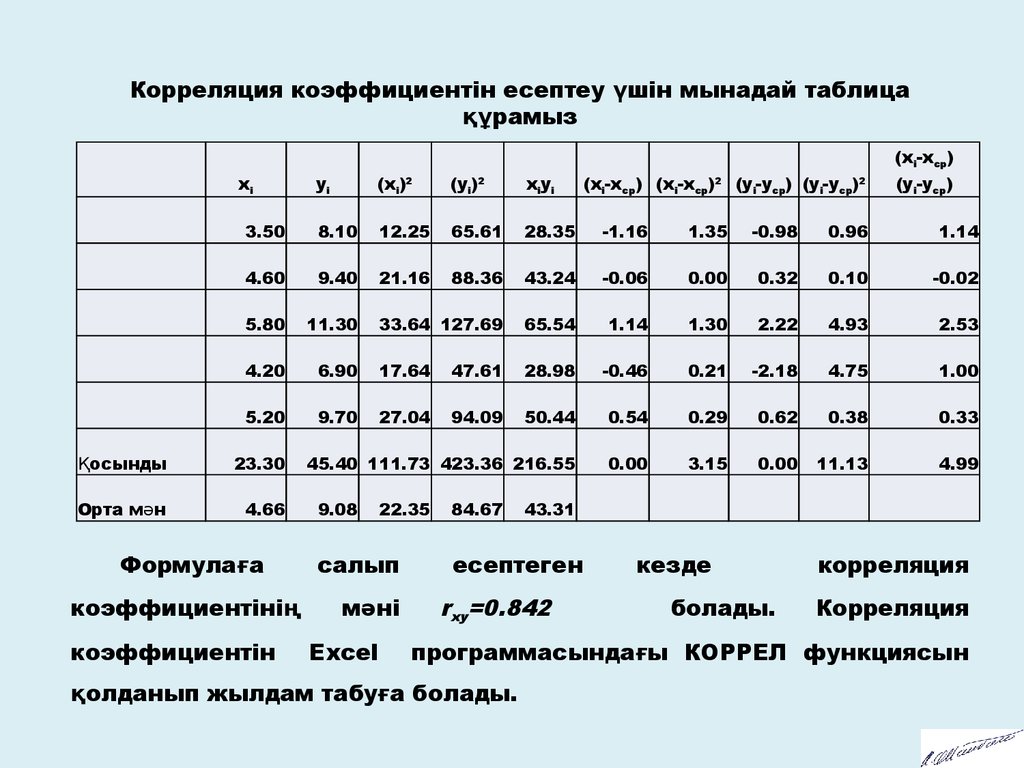
Корреляция коэффициентін есептеу үшін мынадай таблицақұрамыз
(xi-xср)
xi
yi
(xi)2
(yi)2
xiyi
(xi-xср) (xi-xср)2 (yi-yср) (yi-yср)2
(yi-yср)
3.50
8.10
12.25
65.61
28.35
-1.16
1.35
-0.98
0.96
1.14
4.60
9.40
21.16
88.36
43.24
-0.06
0.00
0.32
0.10
-0.02
5.80
11.30
33.64 127.69
65.54
1.14
1.30
2.22
4.93
2.53
4.20
6.90
17.64
47.61
28.98
-0.46
0.21
-2.18
4.75
1.00
5.20
9.70
27.04
94.09
50.44
0.54
0.29
0.62
0.38
0.33
45.40 111.73 423.36 216.55
0.00
3.15
0.00
11.13
4.99
Қосынды
23.30
Орта мән
4.66
Формулаға
коэффициентінің
коэффициентін
9.08
22.35
салып
мәні
Excel
84.67
43.31
есептеген
rxy=0.842
кезде
болады.
корреляция
Корреляция
программасындағы КОРРЕЛ функциясын
қолданып жылдам табуға болады.
15.
Корреляция коэффициентінің маңыздылығын есептеуТаңдама жиынтықтың (выборка) көлемі аз болған кезде корреляция коэффициентінің
маңыздылығын есептеу керек. Ол үшін Стьюденттің t- критериі қолданылады. Бұл критерийді
қолдану үшін мына әуелі мына шама есептелінеді:
te
ryx2
(n 2)
1 ryx2
Сосын осыған сәйкес Стьюденттің критерийінің таблицалық мәні табылады. Оны табу үшін
екі шама қажет: α - маңыздылық деңгейі, df – еркіндік дәрежесі. Бұл жағдай үшін df=n-2 болады, n
таңдау көлемі. Ал 1-α=p саны осы таңдама жиын арқылы есептеліп отырған мәннің шын мәнге
жуықтығының ықтималдығы. Есеп шығарған кезде α=0,10; 0,05; 0,01 мәндерінің бірін алады,
яғни ықтималдықтың p=0,90; 0,95; 0,99 мәндері қарастырылады. Содат кейін таблицадан tT мәні
табылып te мәнімен салыстырылады. Егер te>tT болса корреляция коэффициентінің маңыздылығы
p болғаны.
Ескерту. Стьюдент критериінің мәні ықтималдықтар теориясы мен математикалық
статистика пәнінің кез келген оқу құралының соңында келтіріледі.
16.
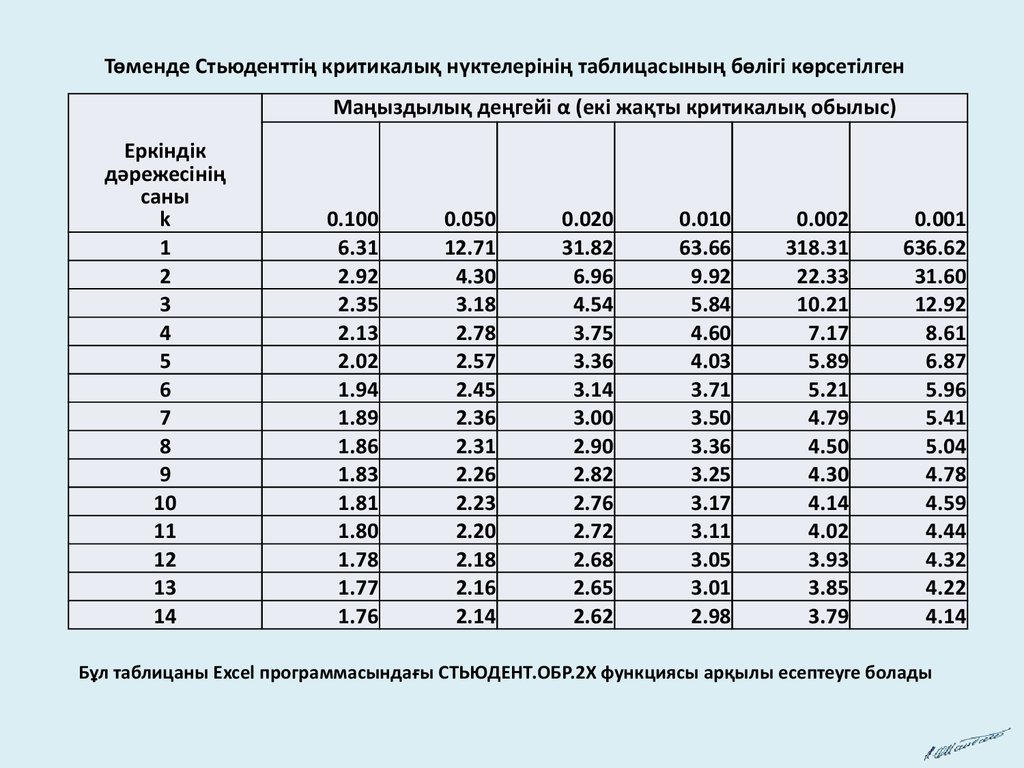
Төменде Стьюденттің критикалық нүктелерінің таблицасының бөлігі көрсетілгенМаңыздылық деңгейі α (екі жақты критикалық обылыс)
Еркіндік
дәрежесінің
саны
k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0.100
6.31
2.92
2.35
2.13
2.02
1.94
1.89
1.86
1.83
1.81
1.80
1.78
1.77
1.76
0.050
12.71
4.30
3.18
2.78
2.57
2.45
2.36
2.31
2.26
2.23
2.20
2.18
2.16
2.14
0.020
31.82
6.96
4.54
3.75
3.36
3.14
3.00
2.90
2.82
2.76
2.72
2.68
2.65
2.62
0.010
63.66
9.92
5.84
4.60
4.03
3.71
3.50
3.36
3.25
3.17
3.11
3.05
3.01
2.98
0.002
318.31
22.33
10.21
7.17
5.89
5.21
4.79
4.50
4.30
4.14
4.02
3.93
3.85
3.79
0.001
636.62
31.60
12.92
8.61
6.87
5.96
5.41
5.04
4.78
4.59
4.44
4.32
4.22
4.14
Бұл таблицаны Excel программасындағы СТЬЮДЕНТ.ОБР.2Х функциясы арқылы есептеуге болады










 mathematics
mathematics economics
economics








