Ең кіші квадраттар принципі. Теңестірудің негізгі әдістері

1. Ең кіші квадраттар принципі. Теңестірудің негізгі әдістері.

Орындаған: Қожақұл Нұрбек

2.

Y = A + B*X + e жұптық сызықтық
регрессияның шынайы моделі.
Оны бағалау үшін үлгі
қолданылады:
(Y1, X1)………(Yn, Xn)
Таңдамалы регрессия теңдеуі
aлынады: Y a b * X

3.

(Yi, Xi) үлгі элементі үшін i = 1,..., n,
жазуға болады:
a
b
*
X
Y
i
i
e Y Y
i
i
i
Y a b*X e
i
i
i

4. Үлгі бойынша регрессия коэффициенттері қалай бағаланады?

5.

Теориялық модельді бағалауымыз керек
үлгі (Yi, Xi) Y = a + b*X + e,графикалық
түрде нүктелердің "бұлты" түрінде
ұсынылады

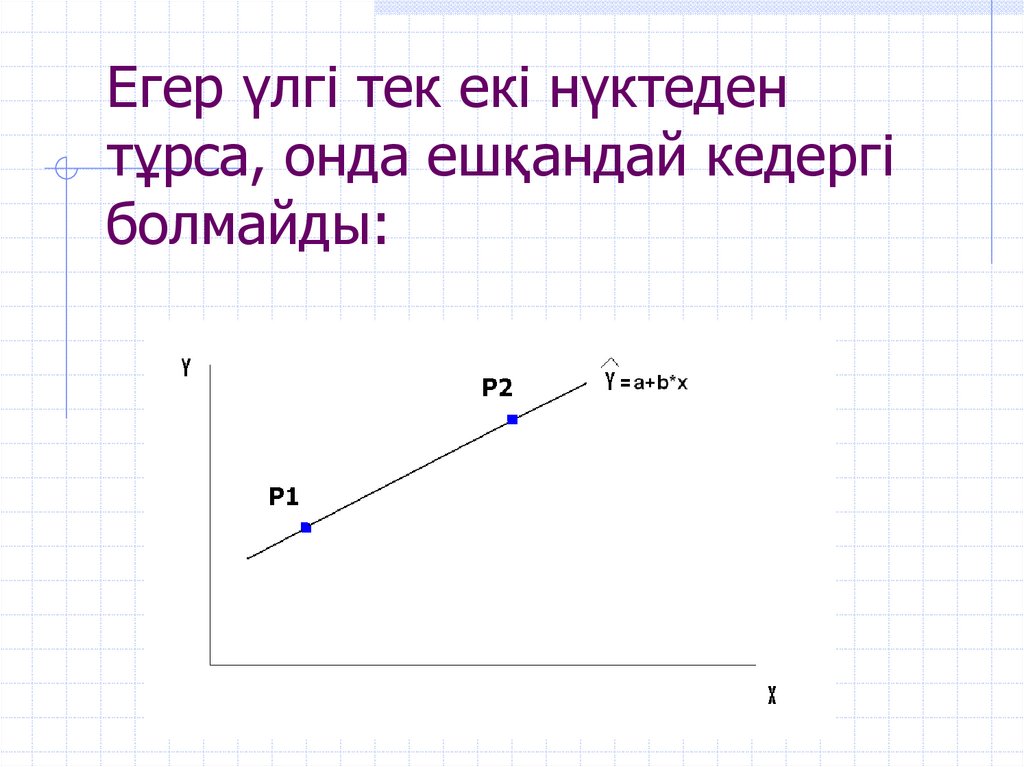
6. Егер үлгі тек екі нүктеден тұрса, онда ешқандай кедергі болмайды:

7. Ең кіші квадраттар әдісінің принципі

Берілген үлгі үшін (X1, Y1), ..., (Xn,
Yn) A және b параметрлері
қалдық квадраттарының
қосындысының минималды
мәнін алатындай етіп
n
2
есептеледі:min
e
i 1
i

8.

Бұл жүйенің шешімі мәндерді береді А және В
регрессия теңдеуінің параметрлерін бағалау үшін:
b
xy x y
x x
2
2
a y b x

9. Анықтау коэффициенті:

2
R ryx
2
- регрессия теңдеуімен түсіндірілетін Y
дисперсиясының бөлігі, яғни х
факторының үлгісіндегі өзгерістер.

10.

Детерминация коэффициенті үлгінің
қаншалықты жақсы екенін көрсетеді y
өзгерістері х өзгерістерімен түсіндіріледі,
яғни таңдамалы регрессия моделі үлгідегі Y
әрекетін қаншалықты жақсы түсіндіреді.
Y факторының өзгеруі оның дисперсиясымен
өлшенеді2(Y).

11. Каких условий?

МНК-оценки a и b являются
случайными величинами, свойства
которых существенным образом
зависят от свойств случайного члена
e модели регрессии.

12. σXi, ei = 0 барлық бақылаулар үшін.

Кездейсоқ термин түсіндіруші
айнымалыға тәуелсіз бөлінеді.
Бұл әрдайым түсіндіруші айнымалылар
кездейсоқ шамалар болмаса
орындалады.

13. Кездейсоқ қателерді есептеу формулалары:

mb
ma
mr
^ 2
(
y
y)
(n m 1) ( x x )
^ 2
(
y
y
)
2
2
x
(n m 1) n ( x x ) 2
1 r
2
yx
n m 1

14. Болжамның сенімділік аралығын есептеу

a a a
b b b
a tтаблma , b tтаблmb
Егер сенімділік интервалының шекараларына нөл түссе,
яғни төменгі шекара теріс, ал жоғарғы шекара оң болса,
онда бағаланатын параметр нөлге тең болады, өйткені ол
бір уақытта оң және теріс мәнді қабылдай алмайды.

15. Назарларыңызға Рахмет!