Similar presentations:
Дифференциальные уравнения
1.
Дифференциальные уравнениДифференциалдық теңдеулер
G(t , y, y ,..., y ( n ) ) 0
y
( n)
F (t , y, y ,..., y
y y (t )
( n 1)
)
2.
Дифференциальные уравненияДифференциалдық теңдеулер
dy
f (t , y, u ),
dt
y (t ) âåêòîð yi (t ), i 1,2,..., m âûõîäíûå ïåðåìåííûå
(ïåðåìåííûå
u u j (t ) âõîäíûå ïåðåìåííûå
ñîñòîÿíèÿ
);
;
f ( x, t , u ) âåêòîð ôóíêöèÿ ïðàâûõ ÷àñòåé óðàâíåíèÿ .
dy
f (t , y , u )
dt
y (t 0 ) y 0
3. Численные методы решения ДУ ДТ сандық әдістерімен шешу
(tm , ym )y f (tm , ym )
'
m
t m 1 t m h
4. Численные методы решения ДУ
Уравнение касательнойy ym y (t t m )
'
m
Из заданного уравнения имеем можем вычислить tg угла
наклона касательной
y m' f (t m , ym )
Следующей точкой решения считаем ту, где касательная
пересечет ординату точки
tm 1 t m h
Тогда
ym 1 ym h f (tm , ym )
ìåòîä
Ýéëåðà
(1)
5. ДТ сандық әдістерімен шешу
Жанама теңдеуіy ym y (t t m )
'
m
Берілген теңдеуден жанаманың иілу бұрышының tg есептей
аламыз
y f (t m , ym )
'
m
Шешімнің келесі нүктесі деп жанама келесі нұктенің
ординатасымен қиылысу нүктесін аламыз
tm 1 t m h
Сонда
ym 1 ym h f (tm , ym )
- Эйлер әдісі
(1)
6. Численные методы решения ДУ
Методы Рунге-Кутта:1. Одноступенчатые;
p
2. Порядок точности - порядок метода h .
3. Не требуется вычислений производных функции.
Метод Эйлера – метод Рунге-Кутта первого порядка точности.
7. ДТ сандық әдістерімен шешу
Рунге_Кутт әдістері:1. Бірқадамды;
2. Дәлдік реті – әдіс реті h p .
3. Функциялардың туындыларын есептеу қажет емес.
Эйлер әдісі – дәлдігі бірінші Рунге-Кутт әдісі.
8. Численные методы решения ДУ ДТ сандық әдістерімен шешу
t m , ymt m h, ym h y
'
m
1
F1 (t m , y m , h) [ f ( xm , y m ) f ( xm h, y m h y m' ), a y m' f ( xm , y m )
2
y ym h F1 (tm , ym , h)
ym 1 ym h F1 (tm , ym , h)
-исправленный метод Эйлера
- түзетілген Эйлер әдісі
(2)
9. Численные методы решения ДУ ДТ сандық әдістерімен шешу
hh '
'
F2 (t m , y m , h) f ( xm , y m y m ), a y m f ( xm , y m )
2
2
ym 1 ym h F2 (tm , ym , h)
- модифицированный метод Эйлера
(3)
10.
Численные методы решения ДУДТ сандық әдістерімен шешу
Төртінші ретті дәлдігі бар Рунге-Кутт әдісі
y m 1
h
y m ( k1 2 k 2 2 k 3 k 4 )
6
где
k1 f ( x m , y m )
h k1
h
k 2 f ( xm , y m
)
2
2
h k2
h
k 3 f ( xm , y m
)
2
2
k 4 f ( x m h, y m h k 3 )
11.
Численные методы решения ДУДТ сандық әдістерімен шешу
y y,
'
y ( 0) 1
12.
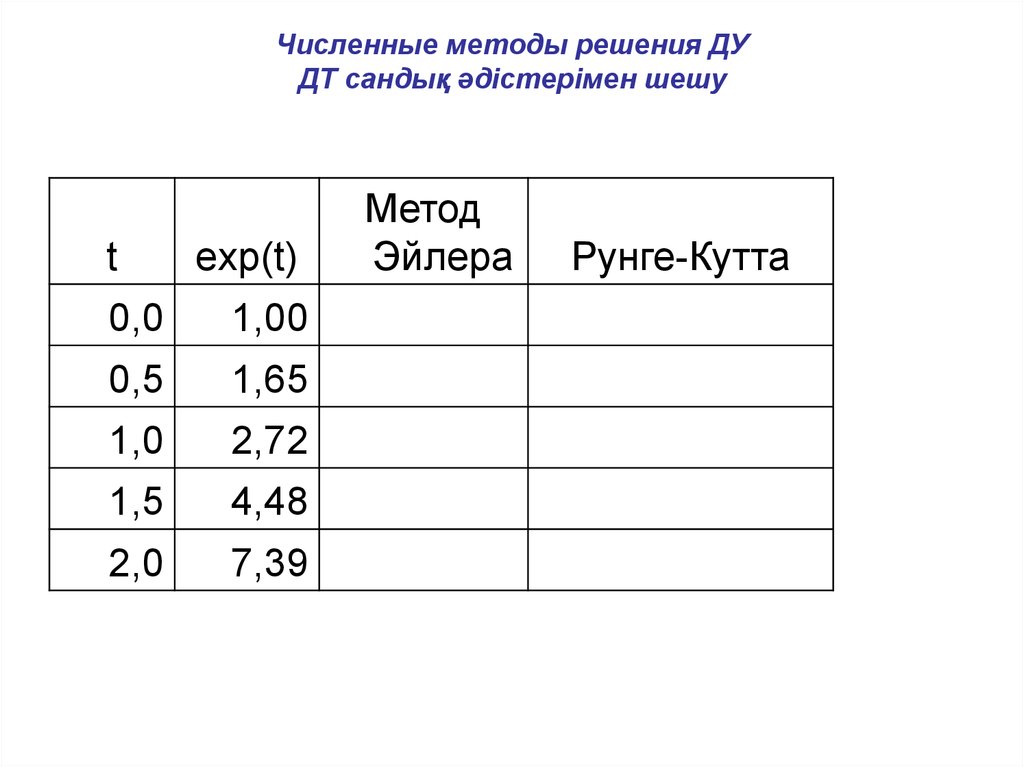
Численные методы решения ДУДТ сандық әдістерімен шешу
t
exp(t)
0,0
1,00
0,5
1,65
1,0
2,72
1,5
4,48
2,0
7,39
Метод
Эйлера
Рунге-Кутта
13.
Численные методы решения ДУДТ сандық әдістерімен шешу
8,00
7,00
6,00
5,00
4,00
3,00
2,00
1,00
0,00
1
2
3
4
5
14.
Численные методы решения ДУДТ сандық әдістерімен шешу
k1 y m
h
k 2 ym ym
2
h
h
k 3 y m ( y m y m )
2
2
h
h
k 4 y m h [ y m ( y m y m )]
2
2
h2 h3 h4
y m 1 y m (1 h )
2 6 24













 mathematics
mathematics








