Сызықты емес элементтер бар электр тізбектері және оларды есептеу әдістері.Таралған параметрлі тізбек жайындағы ұғымдар

1. Сызықты емес элементтер бар электр тізбектері және оларды есептеу әдістері.Таралған параметрлі тізбек жайындағы ұғымдар. Ұзын

желінің теңдеулері. Біртектес желідегі орныққан режім.
Ұзын желі дегеніміз, ол ұзындығы толқын ұзындығына теңесетіндей немесе
одан қанша болса да артып кететін желіні айтамыз. Желі- электр
энергияларын немесе сигналдарды жеткізу үшін генератор мен
қабылдағыштарды жалғастыратын желілік сымдар жүйелері.
Желілік сым деп ұзындығы көлденең қима өлшемінен әлдеқайда үлкен
сымды айтады. Ұзын желінің қарапайым мысалы ретінде l ұзындығы бар
желілік сым жер бетінен h биіктікте оқшаулатқыштың көмегімен ағаш
немесе темірбетон тіректерге іліп қойылған, оның бір ұшына синусоидалы
Э.Қ.К. бар генератор қосылған, екінші ұшына жүктеме кедергісі қосылған.
Егер болса сұлбада шоғырланған Z1 және Z2 элементтері болады. l - желілік
сым генератор мен жүктемені жалғайтын сым міндетін атқарады, ол ұзын
желі болып саналмайды, - толқын ұзындығы. Егер l ұзындығы
салыстырғанда аса кіші болмаса, онда сұлбада шоғырланған Z1 және Z2
элементтер болады және барлық ұзындық бойынша сымның L0 индуктивтігі,
сымдар мен жер арасындағы C0 сыйымдылығы, R0 активті кедергісі
оқшаулатқыштың g 0 өткізгіштігі таралған.

2.

Егер l болса, онда сұлбада шоғырланған Z1 және Z2 элементтерінің
барлық l желі ұзындығы бойында L0 сымның индуктивтігі, сым мен жер
арасындағы C0 сыйымдылығы, R0 активті кедергісі және оқшаулама g 0
өткізгіштігі таралған. Сым материалдары – мыс, биометалл немесе болат,
алюминий болып келеді. Біріншілік параметрлерге жататындар: L0 индуктивтік, C0 -сыйымдылық, R0 - активті кедергі және g 0 - оқшаулама
өткізгіштігі болып саналады.
Біріншілік параметрлердің тұрақтылығын сақтау үшін бірқатар шарттар
орындалуға тиісті:
- барлық желі ұзындығы бойында сымдардың диаметрі бірдей болуға тиісті,
- желі сымдарының ара қашықтықтары өзгеріссіз қалуға тиісті,
- желі сымдары біртекті материалдардан жасалуы керек,
- әуе желілері сымдарының әркайсысы жерден бірдей биіктікте орналасуы
керек,
- желі астындағы және оның өн бойындағы электрлік қасиеттері бірқалыпты
болуға тиісті,
- барлық желінің өн бойында әрбір сымдар айналадағы ортада бірдей
жағдайда болуға тиісті.

3.

Бұл келтірілген жағдайлардың жиынтығын қамтамасыз ету мүмкін емес,
сондықтан қарастырылған біртектес желілердің мұндай шарттары
идеализацияланған деп саналады.
Желідегі кернеу және ток екі тәуелсіз айнымалының функциясы болып
саналады. Бақылау орнын анықтайтын кеңістік координатасы Х және
бақылау моментін анықтайтын уақыт t координатасы: i i х, t ; u u .х, t
Егер санақ басын желі басы деп қабылдасақ, онда өсінің оң бағыты токтың
оң бағытымен бағыттас келеді.
Біртектес желінің біріншілік параметлерін белгілі деп санасақ, оны бірлік
ұзындығына қатысты қарағанда: R0 - тура және кері сымдырдың кедергілері,
L0 - тура және кері сымдардан құрылған тұзақтардың индуктивтігі,
g 0 - сымдар арасындағы өткізгіштік, C0 -сымдар арасындағы сыйымдылық.
Ұзын желілерді, көптеген тізбектес жалғанған шексіз кішкентай элементар
dx ұзындықты желі түрінде көрсетуге болады, олардың әрқайсысының
кедергілері R0 dх , индуктивтіктері L0 dх , өткізгіштіктері g 0 dх және
сыйымдылығы С 0 dх - тең деп қабылданады:

4.

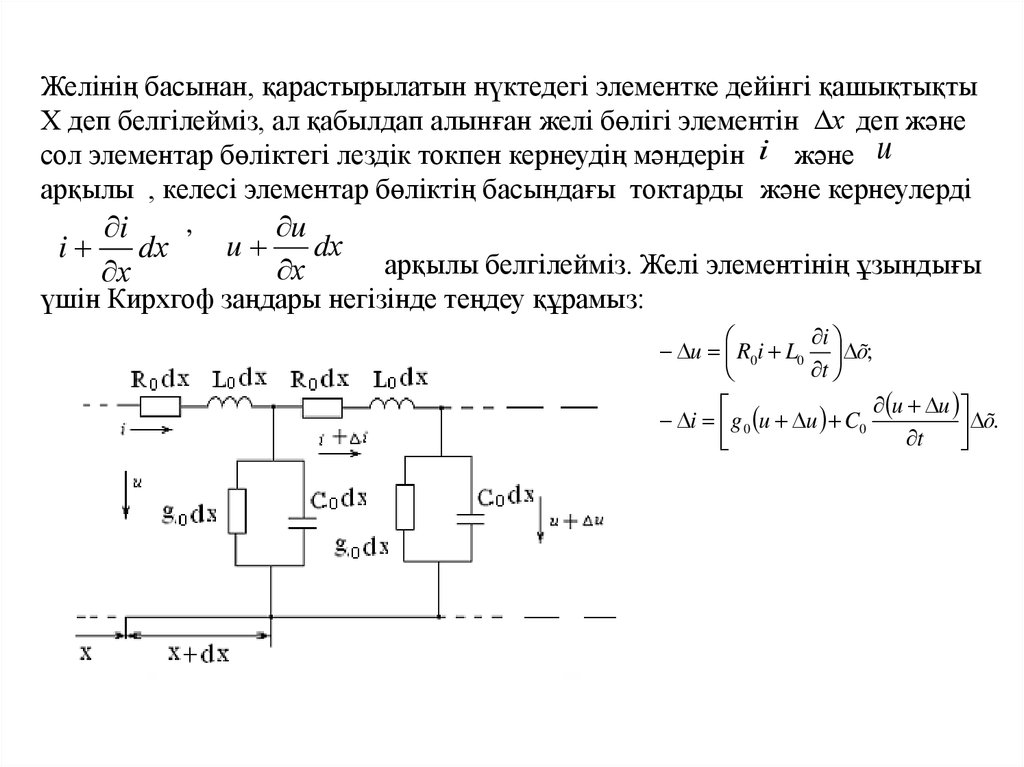
Желінің басынан, қарастырылатын нүктедегі элементке дейінгі қашықтықты
Х деп белгілейміз, ал қабылдап алынған желі бөлігі элементін х деп және
сол элементар бөліктегі лездік токпен кернеудің мәндерін i және u
арқылы , келесі элементар бөліктің басындағы токтарды және кернеулерді
,
u
i
u
dх
i dх
арқылы белгілейміз. Желі элементінің ұзындығы
х
х
үшін Кирхгоф заңдары негізінде теңдеу құрамыз:
i
u R0i L0 õ;
t
u u
i g 0 u u C0
õ.
t

5.

Жақшаны ашып ұқсас мүшелерін жиыстырып, екінші ретті кішілік
шамаларды еске алмай, екі жағында х қысқартсақ, келесі
дифференциалдық теңдеуді аламыз:
u
i
Ri L ,
х
t
i
u
gu C .
х
t
Бұл теңдеулер оқулықтарда телеграфтық теңдеу деп аталады. Егер санақ
бастамасы ретінде желінің соның қабылдасақ, яғни х өсін қабылдығыштан
қоректендіргіш көзіне қарай бағыттасақ, онда теңдеу келесі түрде жазылады:
u
i
R0i L0 ,
õ
t
u
u
g 0 u C0 .
õ
t

6.

Алынған дербес туынды түріндегі теңдеулер жүйесін шешу, бастапқы және
шекаралық шарттылықтар кезінде, желі басынан алынған қашықтық және
уақыттық функция ретінде, токты және кернеуді анықтауға мүмкіндік береді.
Бұл теңдеулер уақытқа қатысты токтардың және кернеулердің кез келген
өзгерістері кезінде әділетті болып саналады.
Біртектес желідегі орныққан режім. Синусоидалы қорек көзі кернеуінің
әрекеті кезінде ұзын желідегі орныққан режімді қарастырамыз. Орныққан
режім үшін теңдеулурді қайта жазып және комплекстік кернеулерін,
токтарын, кедергілерін, өткізгіштерін енгізіп, алатынымыз:
dU
R I j L I R j L I Z I ,
dх
dI
GU jC U G j C U Y U .
вх
Бұл теңдеулерден токты шығарсақ:
кернеуді шығарсақ:
Егер:
d 2U
R j L G j C U Z Y U
dх 2
d2I
R j L G j C I Z Y I .
dх 2
R j L g j C j
ZY
- таралу коэффициенті
деп аталады.

7.

Сонда:
d 2U
2
U,
dх 2
d2I
2 I.
2
dх
Тұрақты коэффициенті бар екінші ретті сызықты дифференциалды теңдеудің
шешімі келесі түрде жазылады:
U A1e х A2e х A1e х e j х A2e х e j х , мұндағы А1 , А2
интегралдың
комплекстік тұрақтысы, олар есептің шекаралық шарттылықтары көмегімен
анықталуға тиісті.
Ток теңдеу бойынша:
I
ZВ
1
A1 e х A2 e х
R j L
g j C
A1 e х A2 e х
R j L
1
A1 e х A2 e х .
ZВ
R j L
- желінің толқындық кедергісі деп аталады.
g j C

8.

Z B Z C Z C e j
Z 0 j
e ,
Y0
- толқындық кедергісінің аргументі.
GL RC
1
arctg 0
.
2
RG 2 LC
Ток: I A1 e х e j х A 2 e х e j х
ZC
ZC
Кернеу өлшемділігі бар комплексті A1 және A 2 көрсеткіш түрінде
келтіреміз:
A1 A1e j 1 , A2 A2 e j 2
Кернеудің және токтың лездік мәндері:
u 2 A1e х sin t х 1 2 A2e х sin t х 2
i
2 A1 х
2 A2 х
e sin t х 1
e sin t х 2 .
Zc
Zc

9.

Бұл соңғы екі теңдеудің оң жағындағы қосындылардың әрқайсысы Х
координатаның бағыты өсетін немесе кемитін жағына қарай қозғалатын қума
толқын ретінде және оны қозғалыс бағытындағы өшу ретінде қарастыруға
болады.Толқынның фазалық жымдамдығы дегеніміз, ол толқын нүктесінің
жылжығандағы жылдамдығы болады, оның фазасы тұрақты күйінде қалады.
Бұл шарттылық толқынның түсуі үшін келесі түрде жазылады:
t х 1 сопst.
Осыдан уақыт бойынша алынған туындыны нольге теңейміз:
d
t х 0, dх - фазалық жылдамдығы деп аталады.
dt
1
dt
Егер толқын ұзындығы:
2
,
2 f
f , T .
T
Яғни, периодқа тең уақыт ішінде ұзындығына тең қашықтықта толқын
жүгіріп өтеді.