Similar presentations:
Резистивті, сыйымдылықты және индуктивті элементер бірізді және параллель жалғанған синусоидал ток тізбегі
1. Резистивті, сыйымдылықты және индуктивті элементер бірізді және параллель жалғанған синусоидал ток тізбегі. Тармақталмаған
тізбектегікернеу резонансы. Токтар резонансы. Резонанс контурдың жиіліктік
сипаттамалары.
Сыйымдылық C , индуктивтік L және кедергінің R тізбектеп
жалғануынан тұратын сұлба берілген болсын.
Кірер қысқыштардағы кернеу: u U m sin n t u .
Кирхгофтың екінші заңы бойынша :
u u R uL uC R i L
di 1
idt .
dt C
Осындай, синусоидалық уақыт функциясының үш қосындысы u R , u L , u C
және оларды әрі қарай тригонометриялық жолмен түрлендірулер көп еңбекті
талап етеді. Сонда да болса бұл есеп комплекстік әдісіпен жеңілірек
шешіледі.
2.
Осы теңдеуді комплекстік түрде жазайық:I m R j L I m
1
I m U m , U Rm U Lm U C m U m ,
j C
1
I m Z U m ,
I m R j L
j
C
U
Im m
Z
j
Um
Um e u
I m e j i , где
j
1 Ze
R j L
C
1
2
L
1
Х
2
2
C , I U m , .
Z R 2 L
arctg
R Х , arctg
m
i
u
C
R
R
Z
Лездік ток: i I m sin t i .
Элементтердегі кернеу:
U RM I m R U Rm e j u , u R U Rm sin t u R ,
U L m I m j L U L m e
j u L
U Cm
, u L U Lm sin t u L ,
i
1
j
I m j
U C m e 2 U C m e u c , uC U C m sin t C L .
C
3.
Лездік кернеу мен комплекстік кернеуді салыстыра отырып, уақыттықсинусоидалық функцияның дифференциалы мен интегралын бейнелейтін
комплексті түрге ауысатын жай ережені жасауға болады. Синусоидалық
функция оны бейнелейтін комплекстік шамаға ауыстырылады,
дифференциялау j -ге көбейтумен, ал интегралдау j -ға бөлумен
ауыстырылады. Синусоидалық кернеудің қосындысына оны бейнелейтін
векторлардың қосындысы немесе әсер етуші комплекстік кернеудің
қосындысы тура келеді: U R U L U C U
Векторлық диаграмма. Векторлық диаграммаларды үш жағдайға
көрсетеміз.
1. Х L Х С , U L UC , 0
ток кернеуден фаза бойынша артта қалады
2. Х С Х L , UC U L , 0,
ток кернеуден фаза бойынша озады.
3.
Х L Х С , U L UC ,
0,
ток кернеумен фаза бойынша бір-біріне үйлесіп
келеді, тізбекте резонанс режімі болғандығын
көреміз.
4.
Жоғарыда айтқандай векторлық диаграммаларды үш жағдайға көрсетеміз.5.
Параллель қосылған R, L және C элементтерден тұратын электр тізбегінеu U m sin t u . кернеуін берсек, онда осы тізбек арқылы өтетін
синусоидалы ток параллель тармақтар арқылы өтетін токтардың
қосындысына тең болады:
i iR iL iC
u 1
du
udt C
.
R L
dt
u uR uL uC .
Комплекстік түрде:
Im
Um Um
j CU m U m G j BL BC U m Y U mY e j u I m e j i .
R
j L
мұндағы:
Y
G 2 B 2 ,
arct
BL BC
,
G
I m U mY , i u .
6.
Элементтерден өтетін токтар комплекстік түрде:I Rm
U
U e
m m
R
R
j
I Rm e
I Cm
j i
, I Lm
Um
U m j u 2
e
I Lm e j i ,
j L Х L
Um
U m j u 2
e
I Lm e j i ,
1
Хс
j
C
Лездік мәндер:
i I m sin t i , iR I Rm sin t R , iL I Lm sin t L , iC ICm sin t c
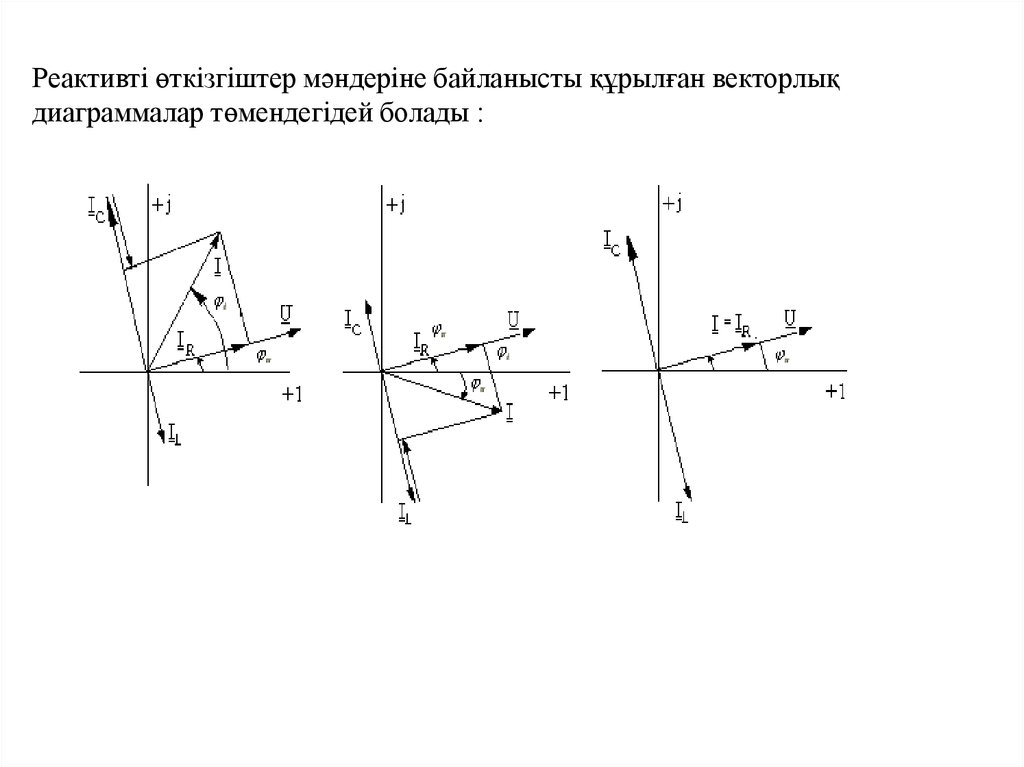
Реактивті өткізгіштер мәндеріне байланысты құрылған векторлық
диаграммалар:
B 0, BL BC , I L I C , 0.
B 0, BL BC , I L I C
B 0, BL BC , I L I C
0
0
7.
Реактивті өткізгіштер мәндеріне байланысты құрылған векторлықдиаграммалар төмендегідей болады :
8. Тармақталмаған тізбектегі кернеу резонансы. Токтар резонансы. Резонанстық контурдың жиіліктік сипаттамалары.
Тізбектей қосылған бөліктері активті кедергіден, индуктивтіктен жәнесыйымдылықтан R, L, C тұратын электр тізбегінде кернеулер резонансы
байқалады. Тізбектей қосылған R, L, C элементтерінен тұратын қарапайым
тармақталмаған тізбекті радиотехникада тербелмелі контур деп атайды.
Кірер кернеу: u U m sin t u , U U e j .
Тізбектің комплекстік кедергісі жиілікке
тәуелді болады:
u
1
Z R j L
R jХ ,
C
Х 0, L
1
C
Z R.
0 L
1
0C
0
1
LC
Кернеудің резонансы 0 -жиілігінде байқалады:
,
.
Кернеулердің резонансы кезінде пайда болатын ток максималдық шамаға
жетеді, оны тікелей Ом заңынан анықтауға болады: I U U I 0
Z
Z 2 R 2 Х 2 , Х 0, Z R.
R
9.
Активті қуат максималды P I U .0
Индуктивтіктегі кернеу сыйымдылықтағы кернеуге шама жағынан бір-біріне
тең болғанымен таңбалары қарама-қарсы болады: U L U C
Реактивті қуаттар бір-біріне тең:
1 2
2
QL QC 0 LI
1
0C
1
1
1
C
C
LC
L
0C
I .
L
C
- тізбектің немесе контурдың сипаттамалық
кедергісі.
Сыйымдылықтағы кернеудің немесе индуктивтіктегі кернеудің кірер
кернеуге қатынасы тізбектің сапалылығы деп аталады:
0 L
UC U L
1
L
0
U
U
0CR
R
L
C
R
R
Q
- контурдың сапалылығы.
Сапалылық дегеніміз, ол резонанс режімі кезіндегі индуктивтіктегі немесе
сыйымдылықтағы кернеу шамасының сұлбаға кіреберістегі кернеуіне
қатынасын айтамыз, немесе U L және U C -ні U мен салыстырғанда қанша
шамаға көп екендігін көрсететін резонанс
10.
режімін айтамыз. Бұл жағдай R шарттылығы орындалған кезде ғанаорындалады. Іс жүзінде Q бірнеше жүздеген шамаға жетуі мүмкін.
Сапалылыққа кері шама
1 өшу коэффициенті деп аталады.
d
Q
Параллель жалғанған R, L, C элементтерден тұратын тізбектегі резонанс
құбылысын ток резонансы дейміз. Кіре берістегі кернеу u U m sin t u .
Тізбектің тармақталмаған бөлігіндегі ток: I U U Y ,
Z
Мұндағы Y - кіре берістегі комплекстік өткізгіштік.
мұндағы B - кіре берістегі
Y G jBL jBC G j BL BC G jB
реактивті өткізгіштік.
1
B
0
,
0
Резонанс кезінде
- резонанс жиілігі.
LC
Токтардың резонансы болған жағдайда сұлбадағы индуктивтік және
сыйымдылық элементтеріндегі токтар шама жағынан бір-біріне тең
I L IC
болғанымен таңбалары қарама-қарсы болады:
Тізбектің сапалылығы:
Q
IC I L
I
I
11.
BLЖиілік сипаттамалары:
Х L L , Х С
1
,
L
BC C ,
B BL BC
1
1
, Х L
С
С
I , U L , U C - резонанстық қисықтар.
U
I
1
R 2 L
C
UC I
1
C
2
I , U L I L
U
1
R L
C
2
2
U
1
R 2 L
C
1
U C .
C
Жиіліктік сипаттамалар және
резонанстық қисықтар суретте
көрсетілген.
2
L U L ,
1
C 0.
L










 physics
physics








