Similar presentations:
Дәріс «Электротехника» курсына кіріспе
1. 1 Дәріс «Электротехника» курсына кіріспе
Пәнніңмақсаты
–
бір
фазалы
синусоидалды және үш фазалы сызықты
электр
тізбектеріндегі
орнатылған
процесстерді
сапа
және
сандық
жақтарынан зерттеу
Пәннің қолданған материалдары
төмендегі курстарда алған білім негізінде
жинақталады:
Жоғары математика
Физика
2. 1 Тарау Сызықты тұрақты ток тізбектері. Элект тізбектің элементтері
Электр тізбек дегеніміз – өз ара байланысқанток жүретін электр энергия көздері және электр
энергия қабылдағыштарының жиынтығы.
Электр энергия көздері дегеніміз – электрлік
есем энергияны (химиялық, жылулық,
механикалық және т.б.) электр энергияға
түрлендіретін құрылғы (гальваникалық
элемент, термоэлемент, генератор және т.б.)
Электрэнергия қабылдағыштары дегеніміз –
электрлік энергияны электрлік емес энергияға
(жарықтық, жылулық, механикалық және т.б.)
түрлендіретін құрылғы (электр шам, жылытқыш
аспап, электр қозғалтқыш және т.б.)
3.
Тек ғана электр энергия көздері бартізбектер активті деп аталады
Тек ғана электр энергия қабылдағыштары
бар тізбектер пассивті деп аталады
4.
Тұрақты ток дегеніміз – уақыт бірлігіндебағыты және шамасы өзгермейтін ток.
Электр ток дегеніміз – электр зарядтардың
реттелген (бағытталған) қозғалысы.
Өткізгіштердің электр тогын өткізу
қабілеттілігі өткізгіштілікпен сипатталады.
Электр энергияны алу, тарату және
түрлендіріуі уақыт бірлігінде тұрақты ток
пен кернеу де жүретін электр тізбектері
тұрақты ток тізбектері деп аталады
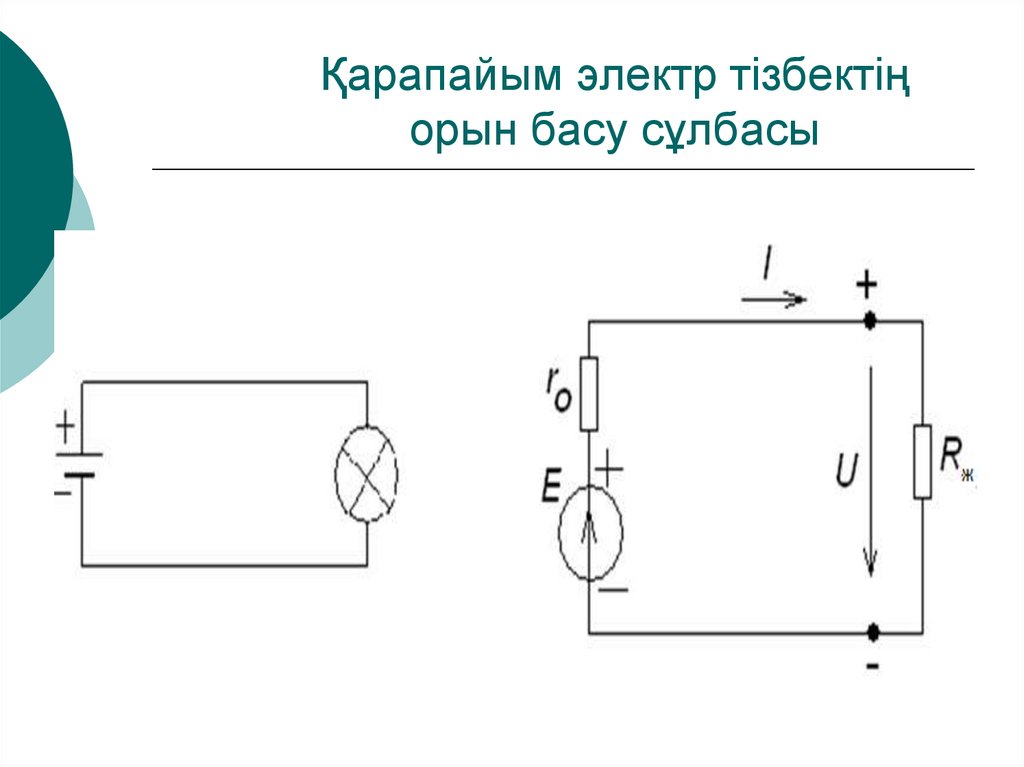
5. Қарапайым электр тізбектің орын басу сұлбасы
6.
ЭҚК әсерінің бағыты энергия көзі ішіндегізарядтар
қозғалысы
сырттан
(электрлік
есмес) берілген күштердің әсерінен болады
да төмен нүкте потенциалынан жоғары нүкте
потенциалына бағытталады.
Кернеу U
дегеніміз – Тізбектің берілген
бөлігінде заряд орын ауыстырғанда, электр
өрісінің атқарған жұмысының осы зарядқа
қатынасын көрсететін шама.
7.
Кедергідегі кернеуді кернеудің төмендеуі депаталады.
Электр тізбектің екі түйін аралығындағы
кернеуінің бағыты жоғары потенциалды
түйіннен
төмен
потенциалды
түйінге
бағытталған.
Электр тізбегінің электр ток өтуіне қарсы
әрекеттілігі электр кедергі деп аталады
Электр тізбегіне қосылатын жәнекедергілерібар
құрылғыларды резисторлар деп атайды
8.
Тұйықталған тізбектегі электр тогы энергиякөзінің ЭҚК-і әсерінен ағады
Токтың шамасы ЭҚК тура пропорционал және
барлық
тізбектегі
кедергісіне
кері
пропорционал.
9. Халқаралық бірліктер жүйесінде:
Ток өлшемінің бірлігі ампер (А) боладыЭҚК және кернеудің өлшемінің бірлігі
вольт (В) болады
Кедергінің өлшемінің бірлігі ом (Ом)
болады
Өткізгіштіктің өлшемінің бірлігі сименс
(См) болады
10. Электр тізбектің жұмыс істеу режімдері
Бос жүріс режімі (жүктемесіз)Rж=∞
Uбж = E
Қысқа тұйықталу режімі
Rж=0
Iбж = 0
Uқт = 0
Қалыпты жұмыс режімі
E
I
Rж r0
Iқт= Е/r0
U E I r0 I Rж
11. Күрделі электр тізбетерінің есебі
Тұрақты токтың күрделі сызықты электртізбегі дегеніміз кез келген тармақталған
электр тізбегі аталады, оның құрамына уақыт
бірлігінде өзгермейтін ток және кернеу (эқк)
көздері, және де сызықты
резисторлар(кедергілері тізбектегі ток және
кернеудің шамасы мен бағытына тәуелді емес)
кіреді.
Күрделі тізбектерді есптеу үшін Кирхгоф
заңдарын және осы заңдарда негізделген
әдістерді пайдаланады.
12.
13.
Күрделі электр тізбекте түйін, тармақ,контур анықталады
Тармақ – дегеніміз бір ғана ток ағатын
(тізбектеп) электр тізбектің элементтерінің
қосылуы
Түйін – дегеніміз үш және одан көп
тармақтардың бір нүктеде қосылуы. Сұлбада
нүкте ретінде көрсетіледі
Контур – дегеніміз бір неше тармақтардаң
жүретін тұйықталған жол
14. Кирхгоф заңдары
I заң1 анықтамасы: Түйіндегі токтардың алгебралық
қосындысы нольге тең
n
I
к 1
n
0
2 анықтамасы: Түйінге келетін токтардың
алгебралық қосындысы осы түйіннен шығатын
токтардың алгебралық қосындысына тең
Түйінге келетін токтар оң бағытты деп алынады,
түйіннен шығатын токтар теріс бағытты деп
алынады.
15.
II Заң1 анықтамасы: Кез келген тұйыұталган контурда
ЭҚК алгебралық қосындысы осы контурдың
кедергілеріндегі кернеулердің төмендеуінің
алгебралық қосындысына тең.
n
n
E I
k 1
n
k 1
n
Rn
2 анықтамасы: Кез келген тұйыұталган контурда
кернеулердің алгебралық қосындысы нольге
n
тең
U
k 1
n
0
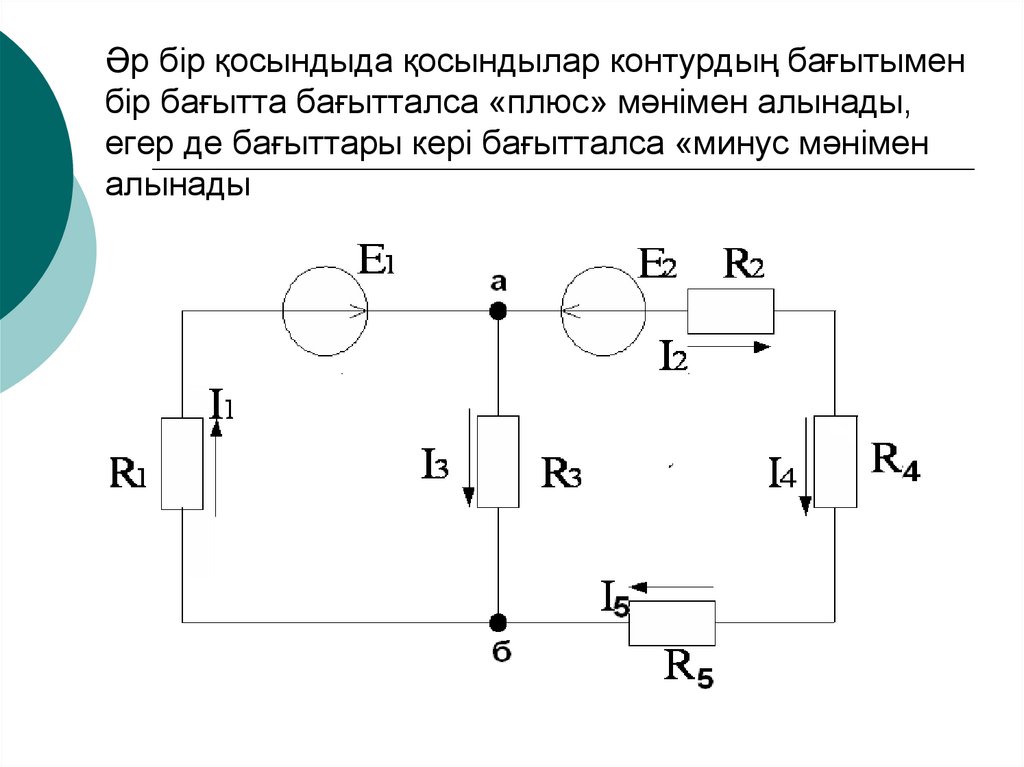
16. Әр бір қосындыда қосындылар контурдың бағытымен бір бағытта бағытталса «плюс» мәнімен алынады, егер де бағыттары кері
бағытталса «минус мәніменалынады
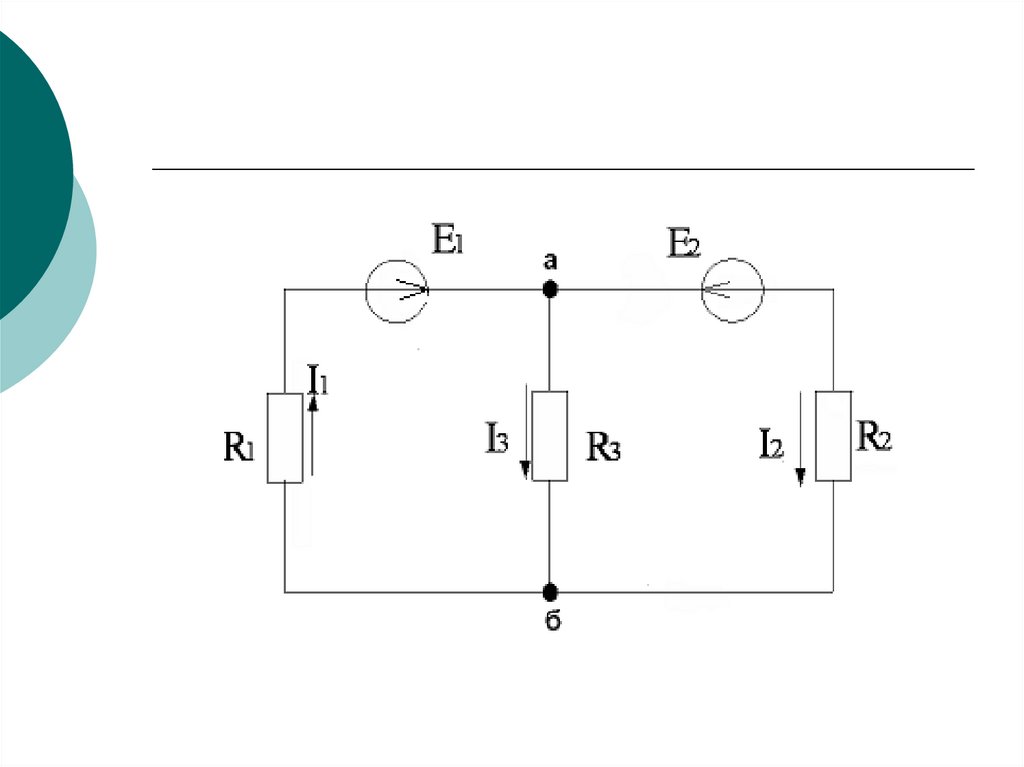
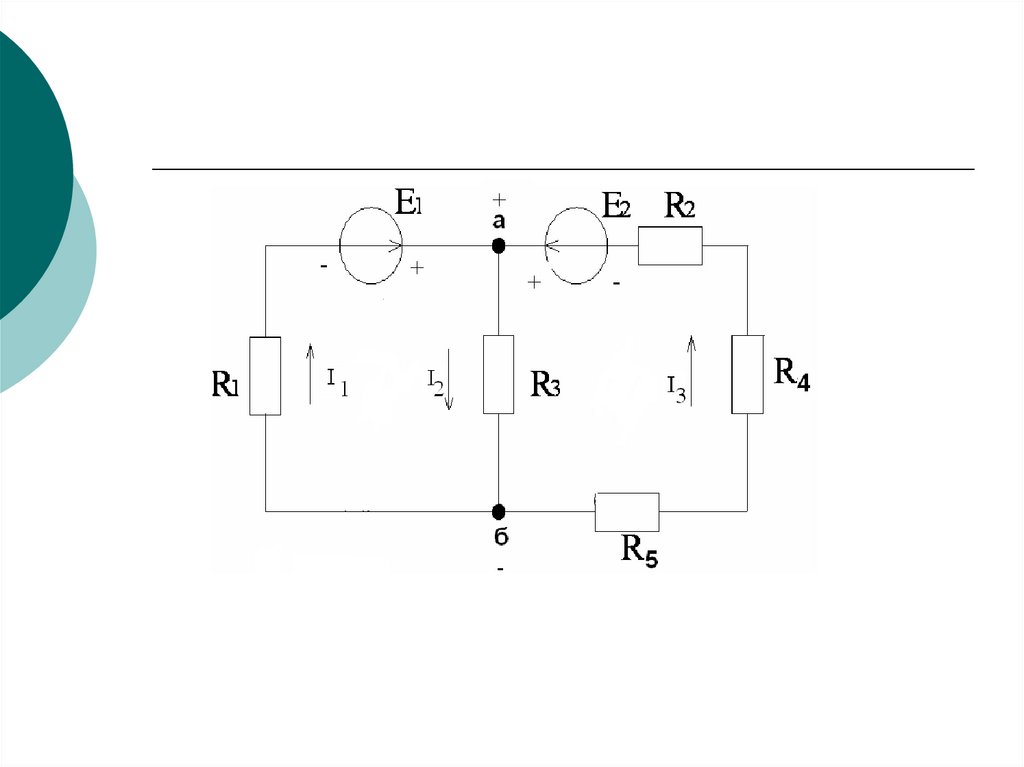
17. Кирхгоф заңдарының пайдаланып тізбектердегі токтарды анықтау
Есеп мақсаты: берілген параметрлер арқылытармақтардағы токтарды анықтау
Тізбектің әр бір тармағында ток ағады, белгісіз
токтардың саны тізбектегі тармақтардың
санына тең.
Өрнектерді құру алдында:
1.
Тармақтағы токтардың оң бағытын таңдап,
сұлбада бағытын көрсетеміз.
2.
Контурдағы ағатын токтың оң бағытын
таңдаймыз(Кирхгофтың II заңы үшін)
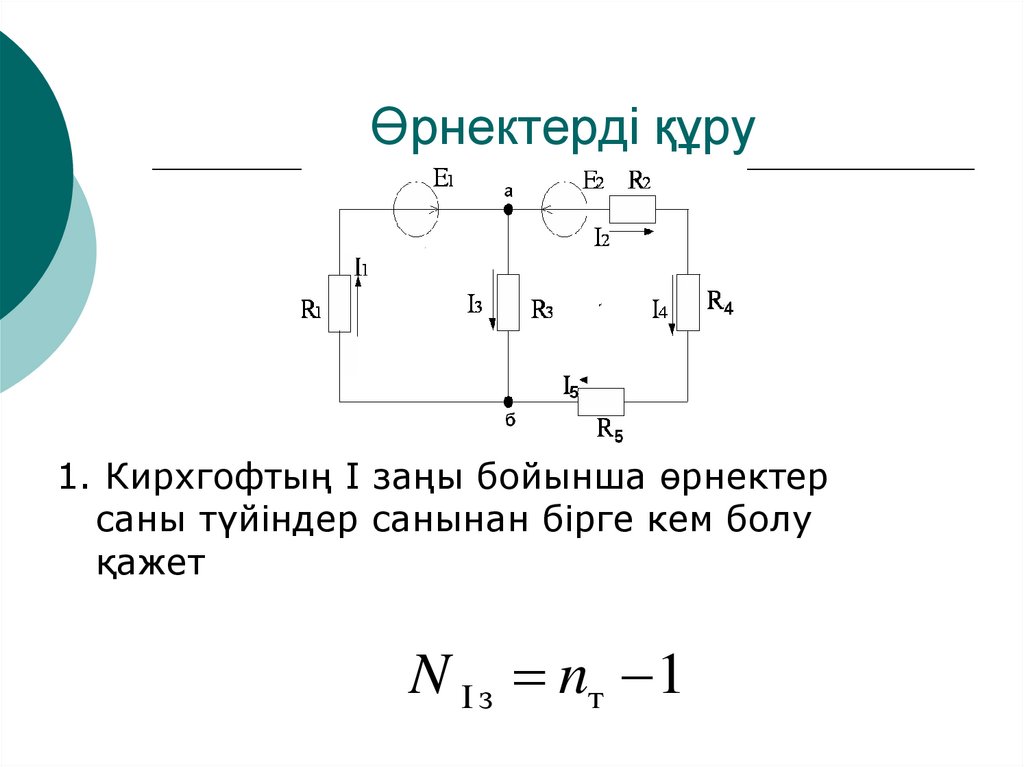
18. Өрнектерді құру
1. Кирхгофтың I заңы бойынша өрнектерсаны түйіндер санынан бірге кем болу
қажет
N I з nт 1
19.
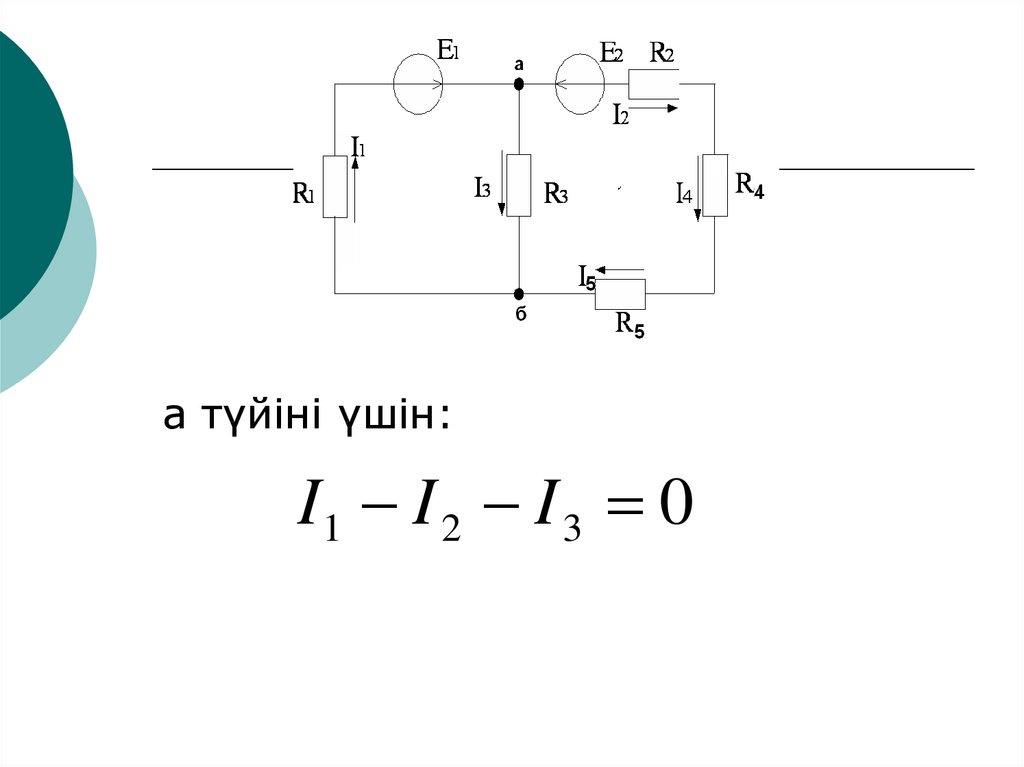
а түйіні үшін:I1 I 2 I 3 0
20.
2. Кирхгофтың II заңы бойынша өрнектерсаны тәуелсіз контурлар санына тең
болу қажет
N IIз nт.к .
Тәуелсіз контур – дегеніміз тым болмаса
бір тармағы басқа контурларға
кірмейтін контур
21.
Сол жақ контур үшін:E1 I1 R1 I 3 R3
Оң жақ контур үшін:
E2 I 2 R2 I 3 R3 I 4 R4 I 5 R5
22. Контурлық токтар әдісі
Бұл бірнеше контуры және электрэнергиясының көзі бар күрделі электр
тізбегін есептеуге арналған кеңінен
таралған әдіс.
Әдіс негізінде Кирхгофтың заңдары мен екі
алғы шарт жатады:
1. Әрбір контурда бір-бірінен тәуелсіз
токтар жүреді, оларды контурлық токтар
деп атайды.
2. Әрбір тармақтағы ток оса тармақтан
жүретін контурлық токтардың алгебралық
қосындысына тең.
23.
Контурлық токтар әдісі бойыншақұралатын өрнектер саны
Nорн nт.к.
24.
1.Өрнектерді құру үшін әрбір
контурлық токтардың бағытын
көрсету қажет.
2.
Кирхгофтың II заңы бойынша
өрнектерді құру қажет
25.
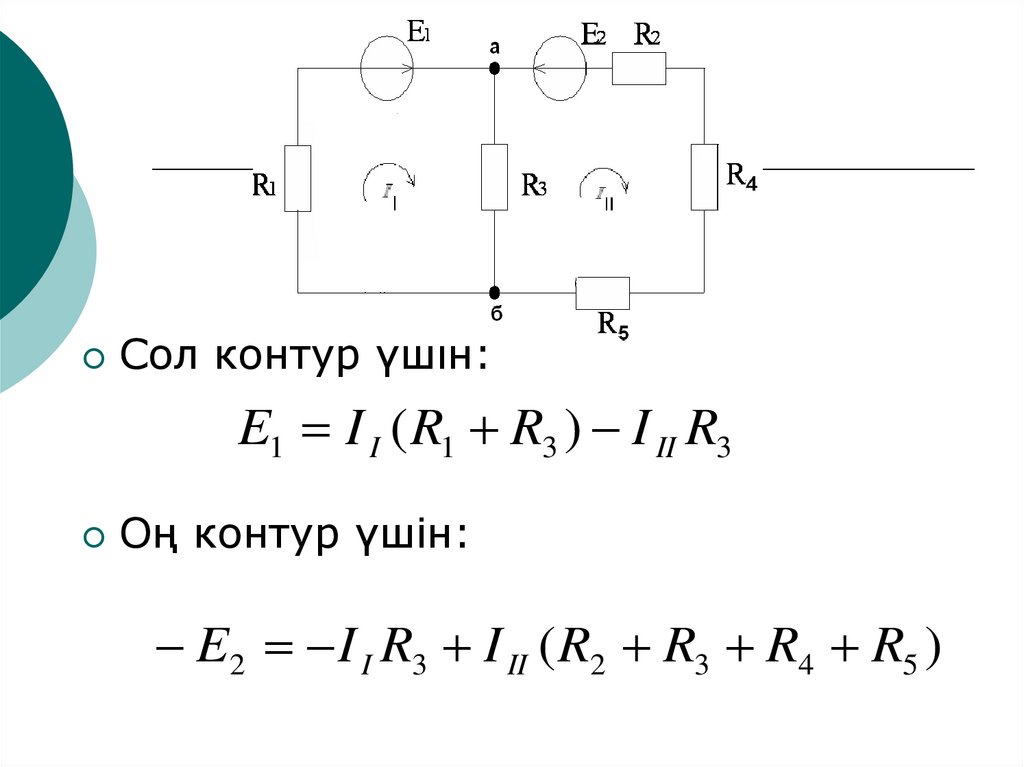
Сол контур үшін:E1 I I ( R1 R3 ) I II R3
Оң контур үшін:
E2 I I R3 I II ( R2 R3 R4 R5 )
26.
Крамер әдісі бойынша контурлықтоктар анықталғаннан кейін,
тармақтардағы токтар анықталады:
1. Егерде тармақ сыртқы болса (Е1, Е2
бірге), онда осы тармақтағы ток мәні
және бағыты бойынша осы контурдағы
токқа тең болады.
2. Егерде тармақ ішкі болса
(R3 бірге), онда осы тармақтағы ток осы
тармақтан жүретін контурлық
токтардың алгебралық қосындысына
тең болады.
27. Қос (екі) түйін әдісі
Бұл әдіс араларында актив жәнепассив тармақтар қосылған екі түйіні
бар электр тізбектерін есептеу үшін
қолданылады.
Әдіс мәні: есептеу өрнегі бойынша екі
түйін арасындағы түйіндік кернеу деп
аталатын Uаб кернеу анықталады,
содан кейін Ом заңы бойынша
тармақтардағы токтар анықталады.
28.
а және б түйіндер арасындағы кернеуU аб
Ек g k
g k
29.
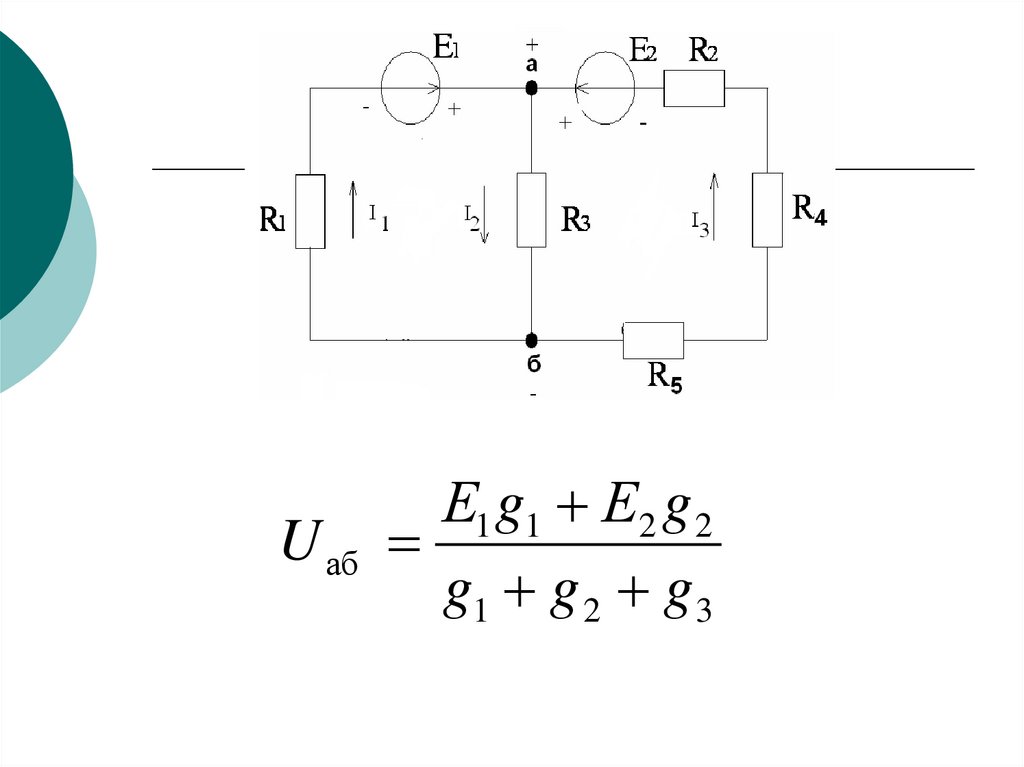
U абЕ1 g1 Е2 g 2
g1 g 2 g 3
30.
мұнда1
g
R
- Тармақтың өткізгіштігі
Ом заңы бойынша әрбір тармақ үшін
өрнек құралады
31.
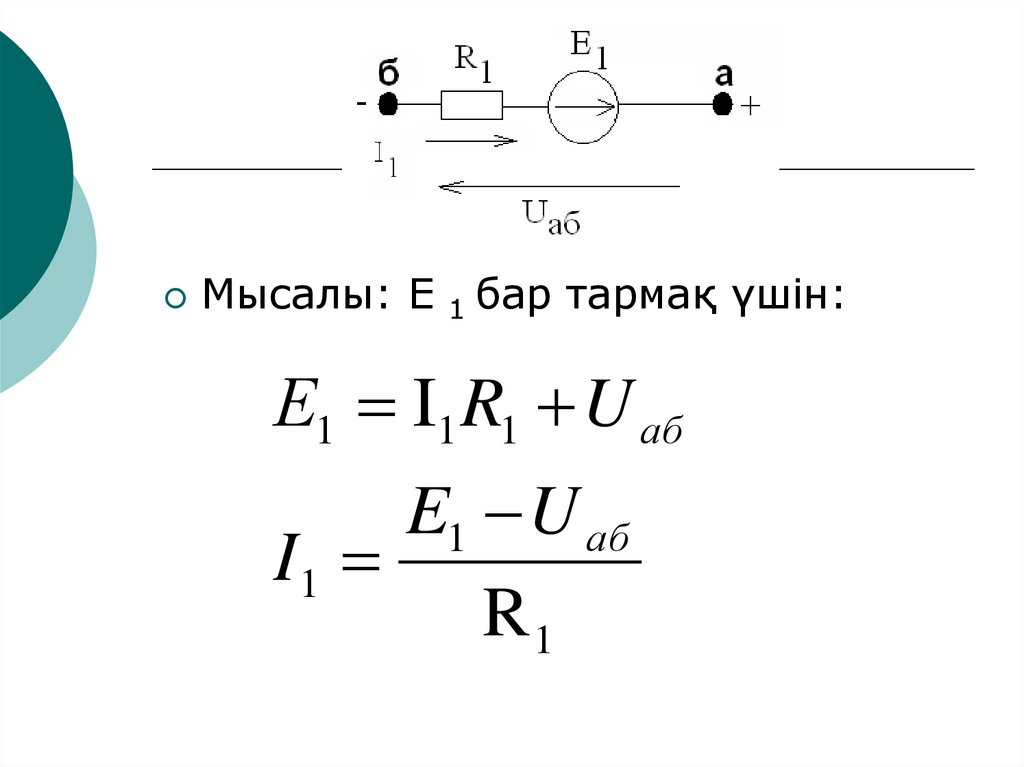
Мысалы: Е1
бар тармақ үшін:
Е1 I1 R1 U aб
E1 U аб
I1
R1
32. Қабатасу принципі мен әдісі
Бұл принцип кез келген сызықтыжүйелердің негізгі қасиеттерінің бірі
болып табылады және сызықты электрлік
тізбектерге қатысты былайша
тұжырымдалады: күрделі электр
тізбегінің қандай да бір тармағындағы ток
тізбекте әрекет ететін электр
энергиясының көздерінің әрқайсысының
осы тізбекте жеке тудыратын дербес
токтарының алгебралық қосындысына
тең
33.
Қабаттасу принципін қолдану көпжағдайда күрделі электр тізбегін
есептеуді жеңілдетеді, өйткені электр
тізбегі бірнеше қарапайым тізбекпен
алмастырады. Бұл тізбектердің
әрқайсысында бір ғана энергия көзі
әрекет етеді. Қабаттасу принципінен
электр тізбектерін есептеуге арналған
қабаттасу әдісі шығады
34. Қабаттасу әдісі
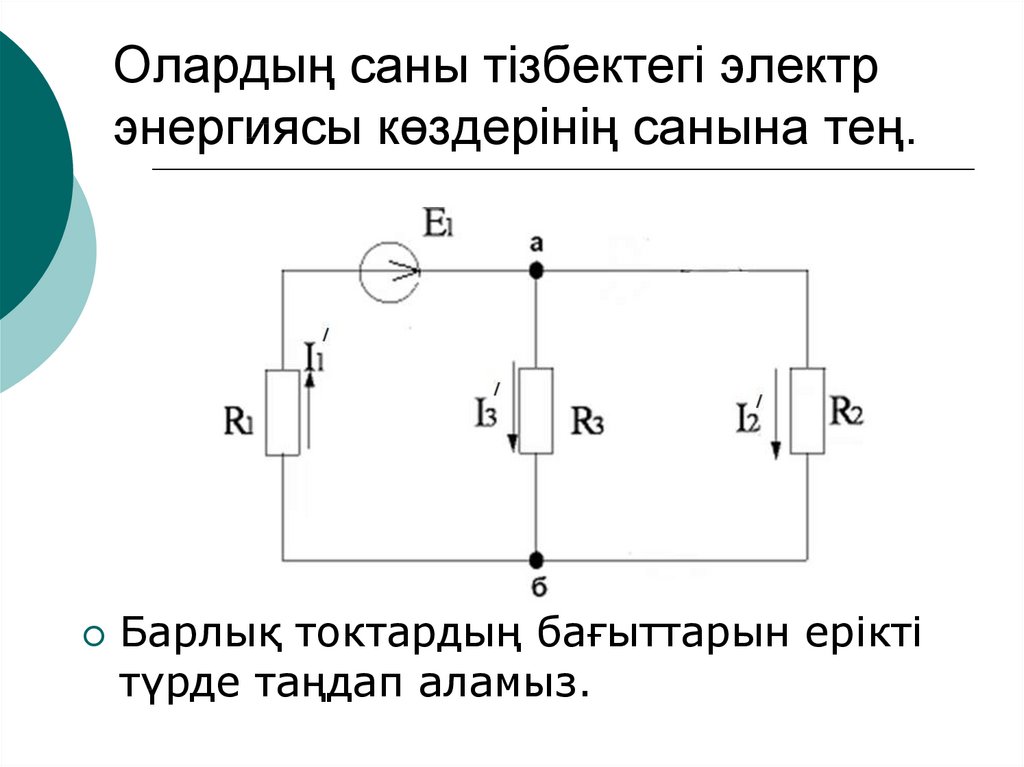
Берілген нұсқаны көмекші нұсқаларғабөлеміз
35. Олардың саны тізбектегі электр энергиясы көздерінің санына тең.
Барлық токтардың бағыттарын еріктітүрде таңдап аламыз.
36.
Көмекші нұсқалардағы токтардыесептейміз. Оларда тек бір ғана ЭҚК
көзі қалтырылады, ал ішкі
кедергілеріді қоса алғанда барлық
кедергілер сақталынады.
1 нұсқа үшін
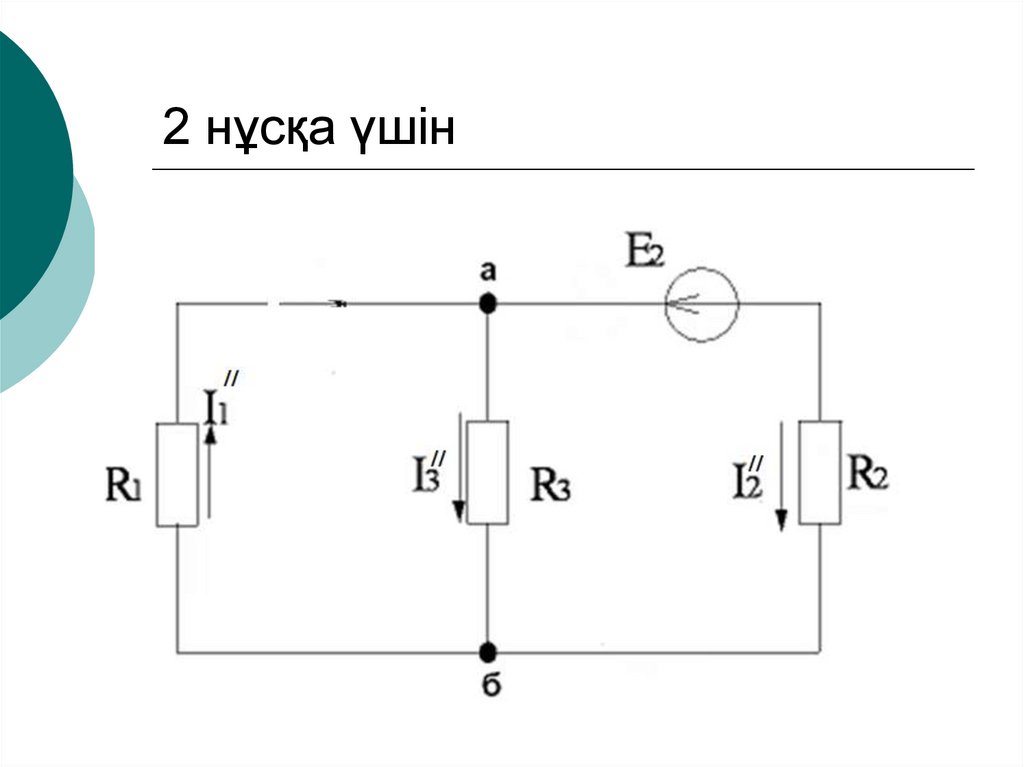
37. 2 нұсқа үшін
38.
39.
Қабаттасу принципі бойынша бастапқыберілген нұсқаныңтармақтарындағы
токтар көмекші нұсқалардың сәйкес
токтарының алгебралық қосындысына
тең
40. Энергетикалық баланс
Энергияның сақталу заңы бойыншаэнергия көздерінің өндіретін қуаты
тізбектебасқа түрге айналатын қуат
мөлшеріне тең болу
Р эн.к. Рж
EI I R
2
41.
Егер токтың оң бағыты ЭҚК-ніңбағытымен сәйкес келсе
жәнеесептелген токтартың мәні оң
болып шықса, онда энергия көзі
энергияны өндіреді (генерациялайды),
яғни генератор режімінде жұмыс
істейді. Егер токтың мәні теріс болып
шықса, онда ЕI көбейтіндісітеріс болып
шығады, яғни энергия көзң тұтынушы
ретінде жұмыс істейді.
42. Электр тізбектің ПӘК-ті
Электр тізбектің ПӘК-ті – бұлқабылдағыш қуатының (пайдалы
қуаттың) барлық тұтынушылардың
қосынды қуатына қатынасына тең
шама
43.
44. Потенциалдық диаграмма
Контурды айналып шығу кезіндегіU(R) тәуелдігінің графигі
45. Бірфазалы айнымалы (синусоидалды) ток электр тізбектері
Айнымалы ток – уақыт бірлігіндемәні мен бағыты өзгеретін ток
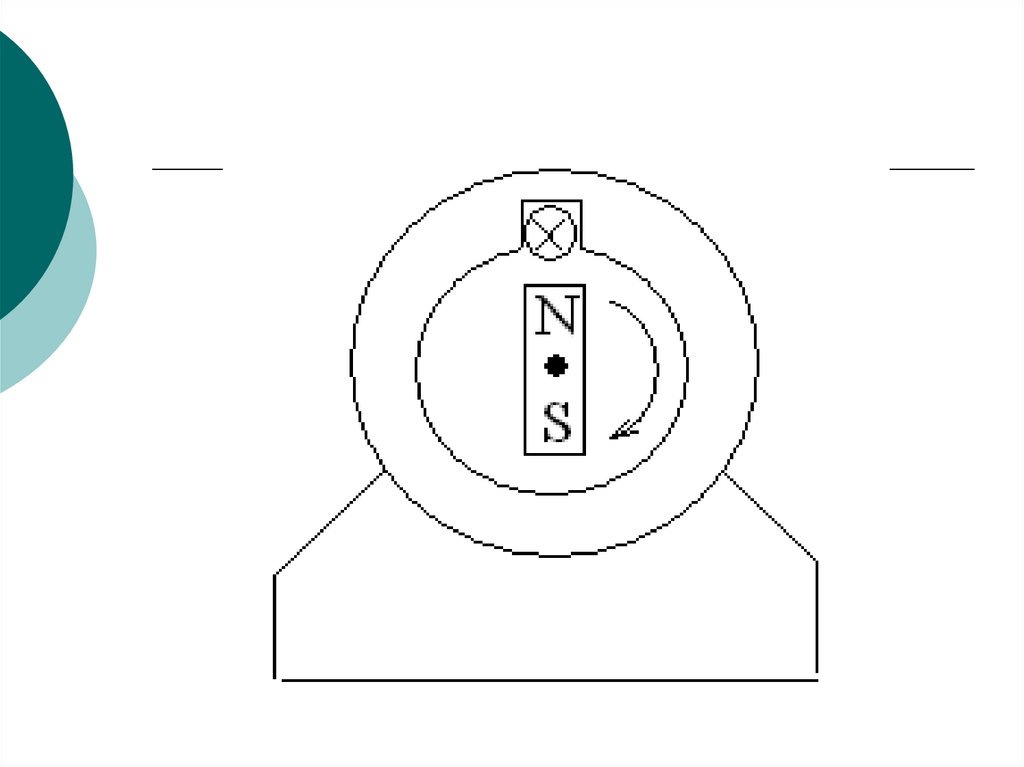
46. Айнымалы токты алу процессі
Айнымалы ток генераторыайналмайтын бөлігі – статор және
айналатын бөлігі – ротордан турады.
Статор паздарында орамалар
орналақан, осы орамалардан
айнымалы кернеу өлшенеді.
Ротордың магнит өрісі айналып
статор орамдарымен қиылысып осы
орамдарда ЭҚК индуциялайды
47.
48.
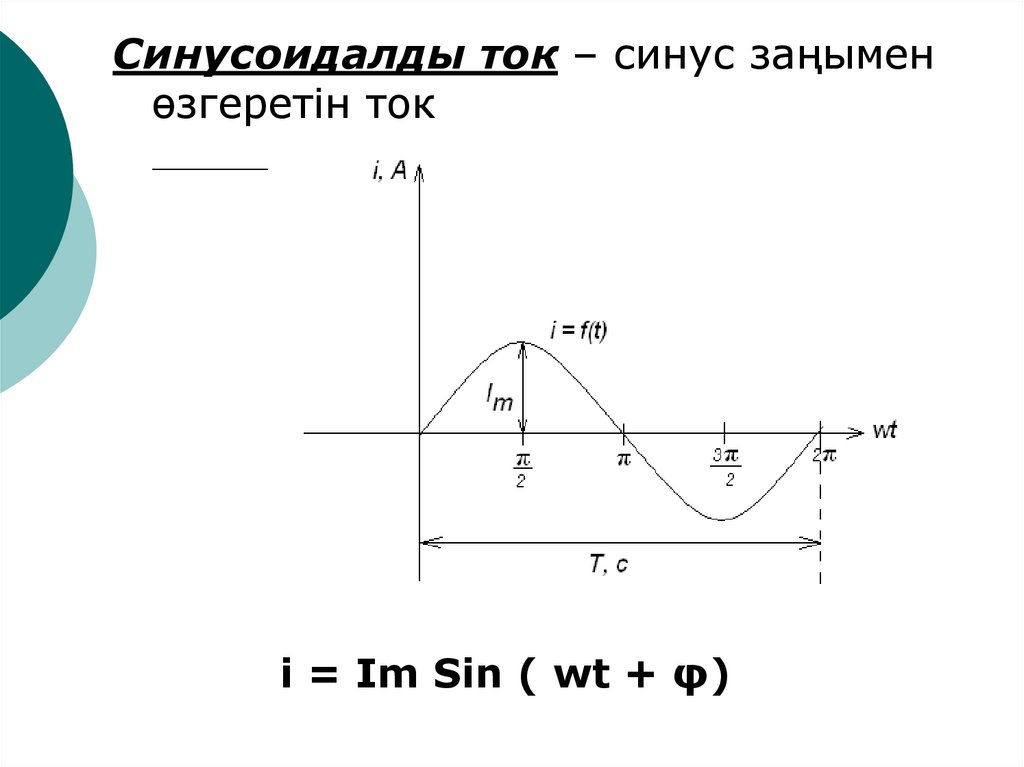
Синусоидалды ток – синус заңыменөзгеретін ток
i = Im Sin ( wt + φ)
49. Синусоидалды токтардың негізгі анықтамалы
i (А), u (В), e (В) лездік мәндері- әр бірберілген уақыт моментіндегі t айнымалы I,
U, E мәндері
Im(А), Um(В), Em(В) амплитудалық
(максималды) мәндері – лездік мәндердің
ең үлкен мәндері
f, (Гц) айнымалы ток жиілігі – периодқа
кері шама, немесе бір секунд ішіндегі
периодтар(тербелістер) саны
1
f
T
50.
Т, с период – временной интервал,за который происходит полный цикл
изменения
w, рад/сек бұрыштық жиілік величина, пропорционально синусу
которой изменяются мгновенные
значения тока, напряжения, ЭДС
2
w 2 f
T
51.
Айнымалы Iорт(A), Uорт(B),Еорт(B) орташа мәндері–
вычисляют за полупериод, в
течении которого величина
остается положительной
I ОРТ
2
U ОРТ
IМ
EОРТ
2
EМ
2
UМ
52.
I (A), U (B), E (B) әрекет етумәндері
I
IM
U
2
E
EM
2
UM
2
53.
φ бастапқы фаза–электрический угол,
определяющий значение тока,
напряжения, ЭДС в начальный
момент времени (t = 0)
54.
Опережающая по фазесинусоидальная величина – та, у
которой положительный полупериод
начинается раньше, чем у другой
синусоидальной величины
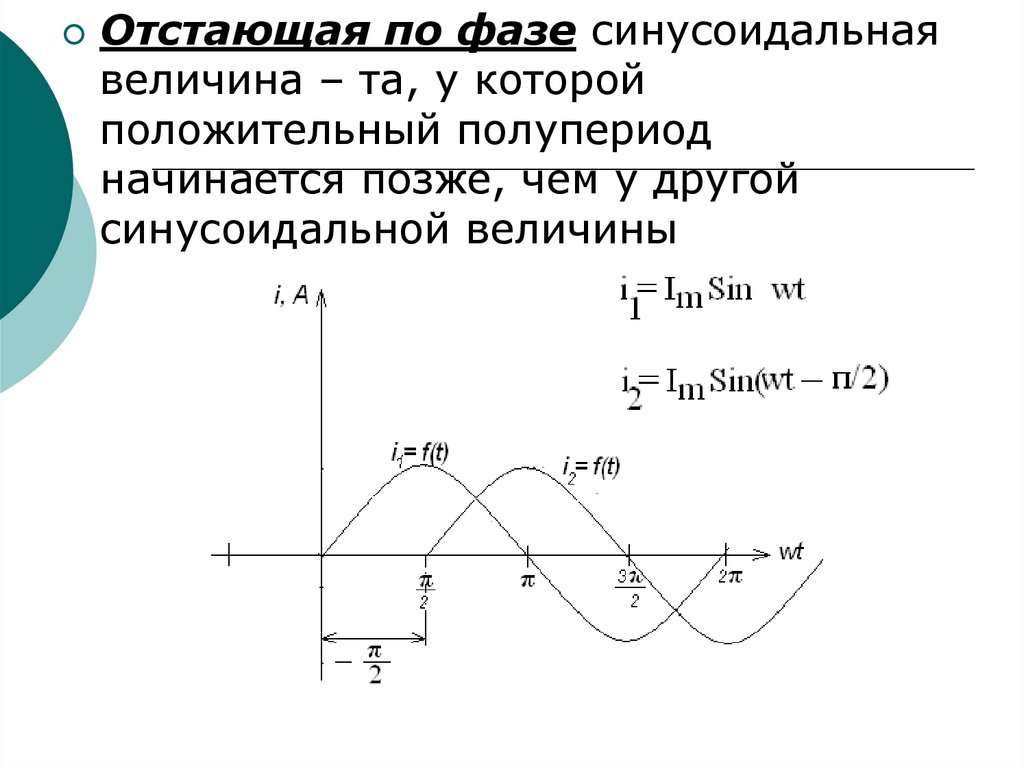
55.
Отстающая по фазе синусоидальнаявеличина – та, у которой
положительный полупериод
начинается позже, чем у другой
синусоидальной величины
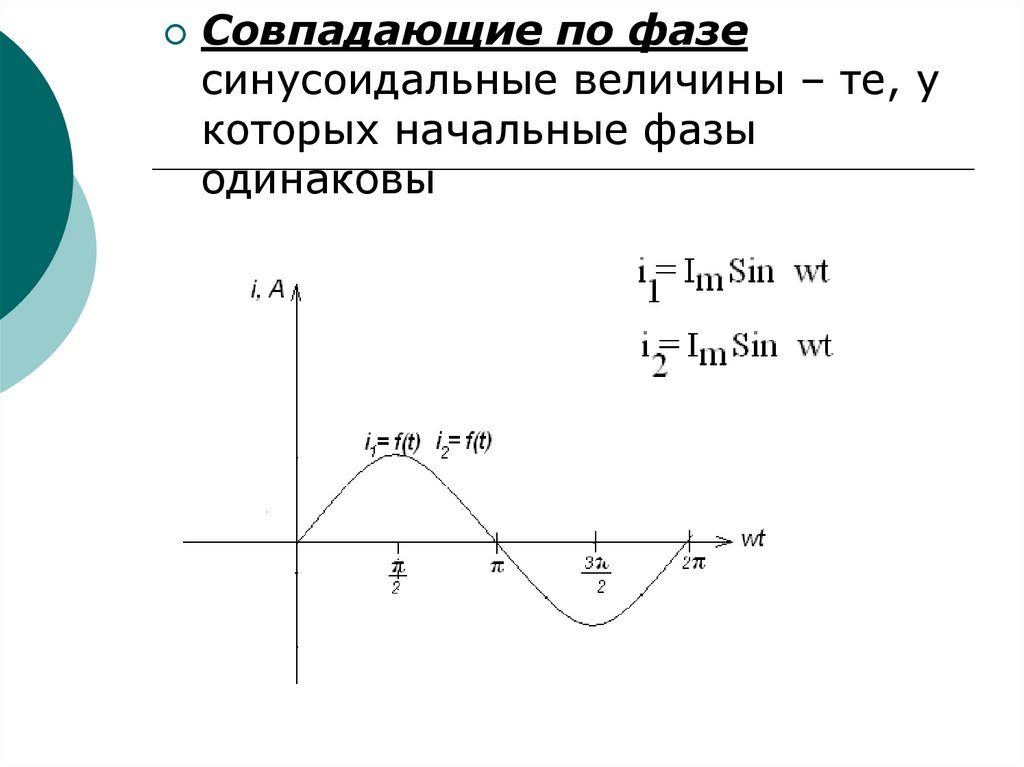
56.
Совпадающие по фазесинусоидальные величины – те, у
которых начальные фазы
одинаковы
57. Изображение синусоидальных функций времени векторами и комплексными числами
Векторной диаграммойназывают совокупность векторов,
изображающих исследуемые
функции времени
58. Расчет электрических цепей синусоидального тока
--
Эл.цепь, в которой происходит
преобразование эл.энергии в
тепловую, и в которой происходит
изменение энергии электрического и
магнитного полей, характеризуется
основными элементами:
Резистором с сопротивлением R
Индуктивной катушкой с
индуктивностью L
Конденсатором с емкостью С
59.
В активном сопротивлении Rпроисходит преобразование
электромагнитной энергии в тепло.
Напряжение на резисторе и ток в нем
связаны законом Ома
u r iR
60.
Элементы, связанные только смагнитным полем, учитывающие его
энергию и явление самоиндукции,
характеризуют индуктивностью L.
При изменении тока i в индуктивности
L возникает ЭДС самоиндукции,
препятствующая изменению тока
di
еl L
dt
61.
Для прохождения тока черезиндуктивность, источник расходует
часть своего напряжения на
преодоление ЭДС самоиндукции.
di
ul еl L
dt
При этом поступающая от него энергия
накапливается в магнитном поле
катушки
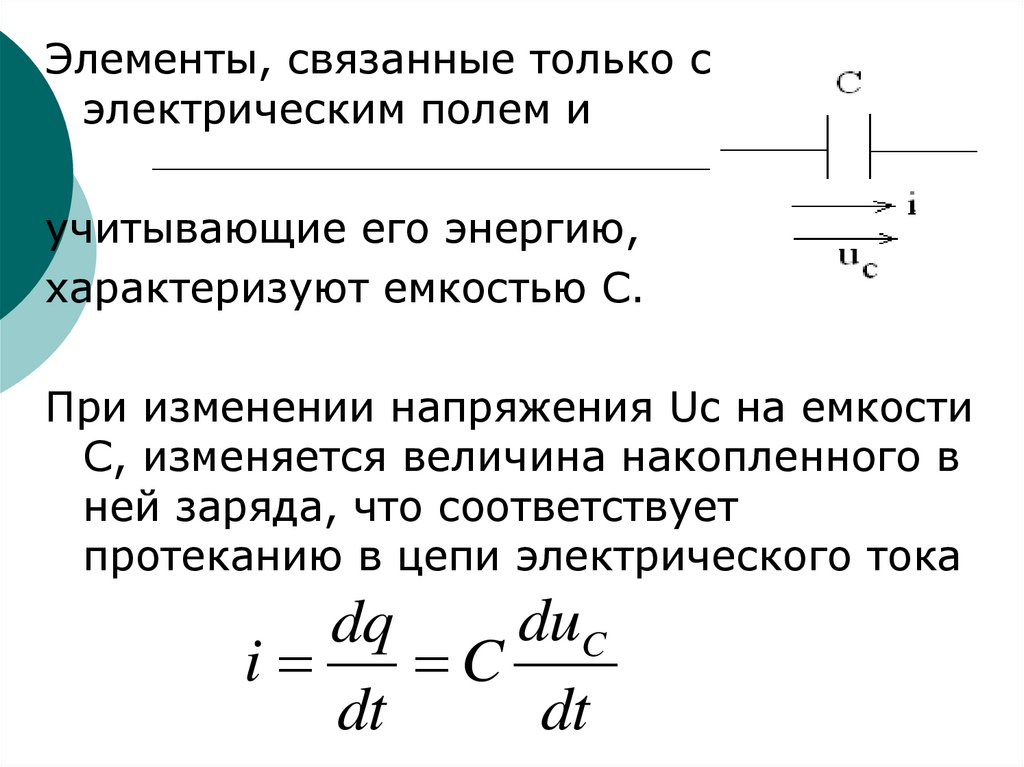
62.
Элементы, связанные только сэлектрическим полем и
учитывающие его энергию,
характеризуют емкостью С.
При изменении напряжения Uc на емкости
С, изменяется величина накопленного в
ней заряда, что соответствует
протеканию в цепи электрического тока
duC
dq
i
C
dt
dt
63. и
Пусть в цепи протекает токi t I m Sin wt
Цепь с сопротивлением R.
По закону Ома, напряжение на
активном сопротивлении
1.
ur RI m Sin wt U m Sin wt
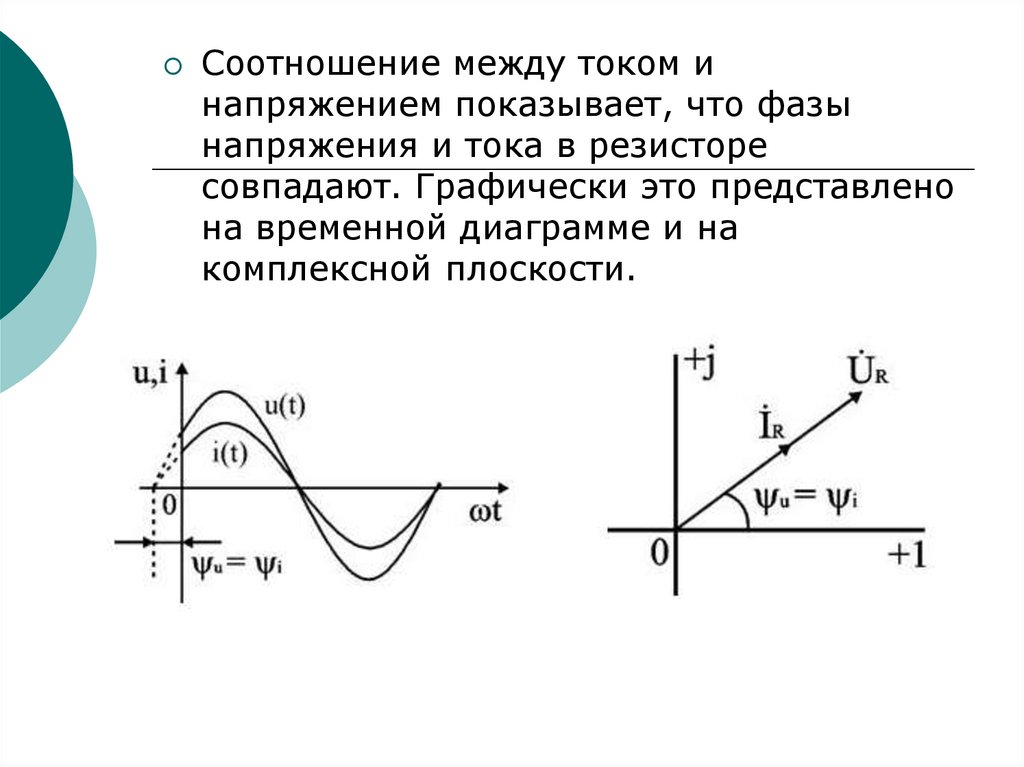
64.
Соотношение между током инапряжением показывает, что фазы
напряжения и тока в резисторе
совпадают. Графически это представлено
на временной диаграмме и на
комплексной плоскости.
65.
2. Цепь с индуктивностью LПод действием синусоидального
напряжения в цепи с индуктивной
катушкой проходит синусоидальный
ток
66.
Зададим изменение тока в индуктивности посинусоидальному закону
i(t) = ImL sin ωt
Используем уравнение связи между током и
напряжением в индуктивности
uL = L · di / dt
и получим
uL(t) = ωL · ImL cos ωt
Заменим cos на sin и получим
uL(t) = ωL · ImL sin(ωt + 90°).
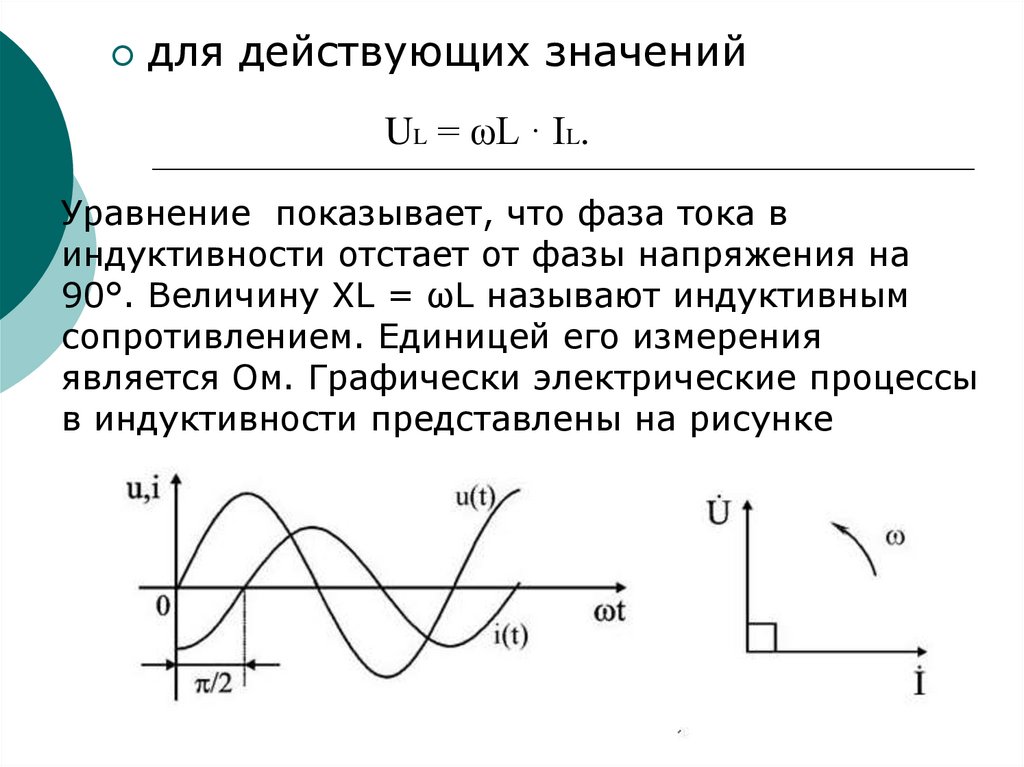
67.
для действующих значенийUL = ωL · IL.
Уравнение показывает, что фаза тока в
индуктивности отстает от фазы напряжения на
90°. Величину XL = ωL называют индуктивным
сопротивлением. Единицей его измерения
является Ом. Графически электрические процессы
в индуктивности представлены на рисунке
68. 3. Цепь с емкостью С
Зададим изменение тока в емкости посинусоидальному закону
i(t) = Imс sin ωt .
Используем уравнение связи
между током и напряжением в
емкости
uC = 1 / C · ∫ i dt,
и получим
uC = 1 / (ωC) · ImC (-cos ωt ).
69.
Заменим –cos на sinuC = 1 / (ωC) · ImC sin(ωt - 90°).
для действующих значений
UC = 1 / (ωC) · IC
Уравнение показывает, что фаза напряжения в емкости
отстает от фазы тока на 90°. Величину XC = 1 / (ωC)
называют емкостным сопротивлением цепи и измеряют его в
Омах. Графически электрические процессы в емкости
представлены на рисунке
70. В цепях переменного тока выделяют следующие виды сопротивлений:
Активное. Активным называют сопротивлениерезистора.
Единицей измерения сопротивления является Ом.
Сопротивление резистора не зависит от частоты.
Условное обозначение
71.
Реактивное. В разделе реактивные выделяюттри вида сопротивлений: индуктивное XL и
емкостное XC и собственно реактивное. Для
индуктивного сопротивления выше была
получена формула XL = ωL. Единицей
измерения индуктивного сопротивления также
является Ом. Величина XL линейно зависит от
частоты.
Для емкостного сопротивления выше была
получена формула XC = 1 / ωC. Единицей
измерения емкостного сопротивления является
Ом. Величина XC зависит от частоты по
обратно-пропорциональному закону. Просто
реактивным сопротивлением цепи называют
величину X = XL - XC
72. Цепь с последовательным соединением элементов R. L. C
Положим, что в этой задаче заданы величины R,L, С, частота f, напряжение U. Требуется
определить ток в цепи и напряжение на
элементах цепи. Из свойства последовательного
соединения следует, что ток во всех элементах
цепи одинаковый. Задача разбивается на ряд
этапов.
73.
1. Определение сопротивлений.Реактивные сопротивления элементов L
и С находим по формулам
XL = ωL,
XC = 1 / ωC,
ω = 2πf.
2. Расчет напряжений на элементах
UR = I R, ψuR = ψi ;
UL = I XL, ψuL = ψi + 90° ;
UC = I XC, ψuC = ψi - 90°.
74.
Для напряжений выполняется второйзакон Кирхгофа в векторной форме.
Ú = ÚR + ÚL + ÚC.
Анализ расчетных данных.
В зависимости от величин L и С возможны
следующие варианты: XL > XC; XL < XC;
X L = X C.
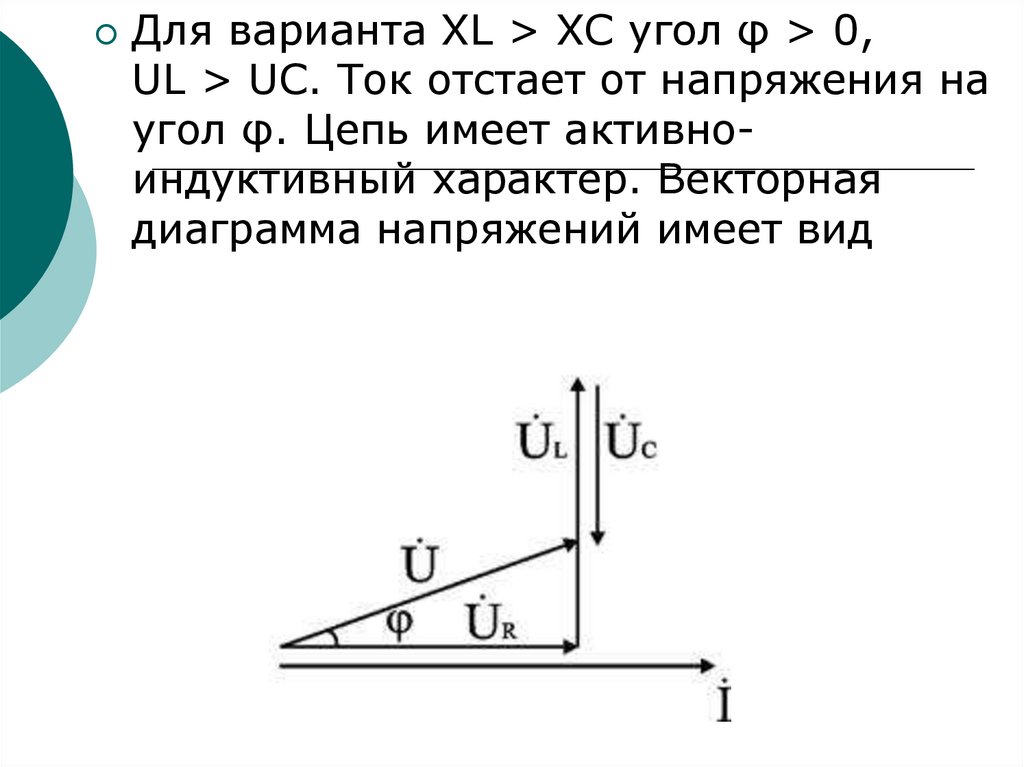
75.
Для варианта XL > XC угол φ > 0,UL > UC. Ток отстает от напряжения на
угол φ. Цепь имеет активноиндуктивный характер. Векторная
диаграмма напряжений имеет вид
76.
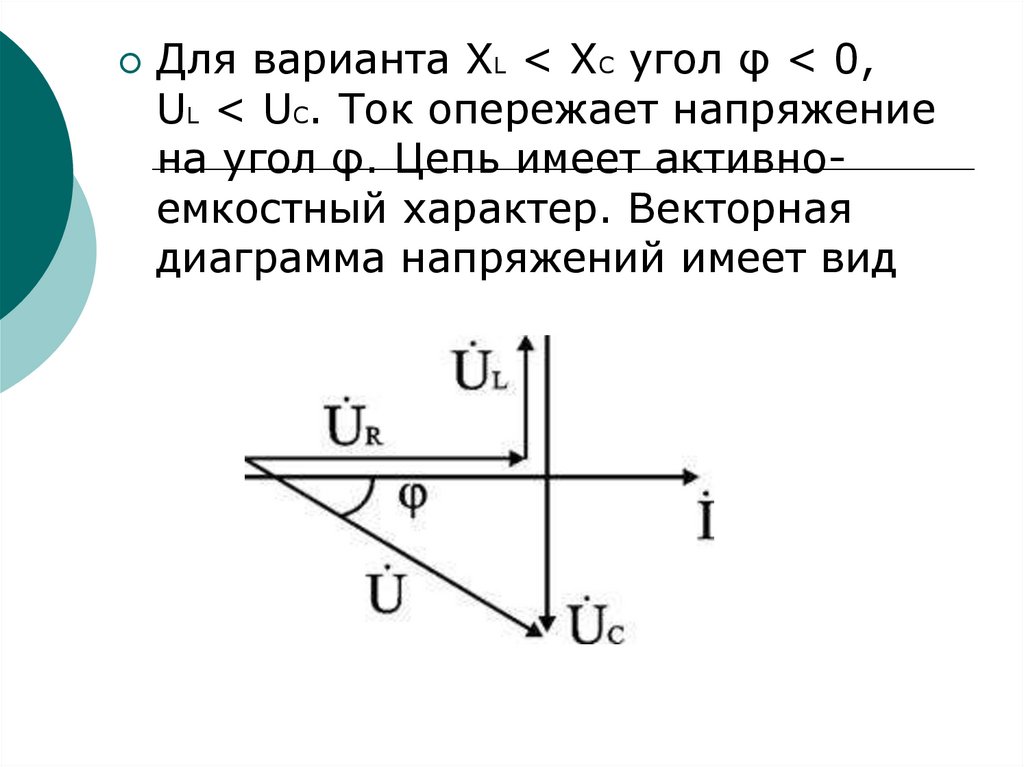
Для варианта XL < XC угол φ < 0,UL < UC. Ток опережает напряжение
на угол φ. Цепь имеет активноемкостный характер. Векторная
диаграмма напряжений имеет вид
77.
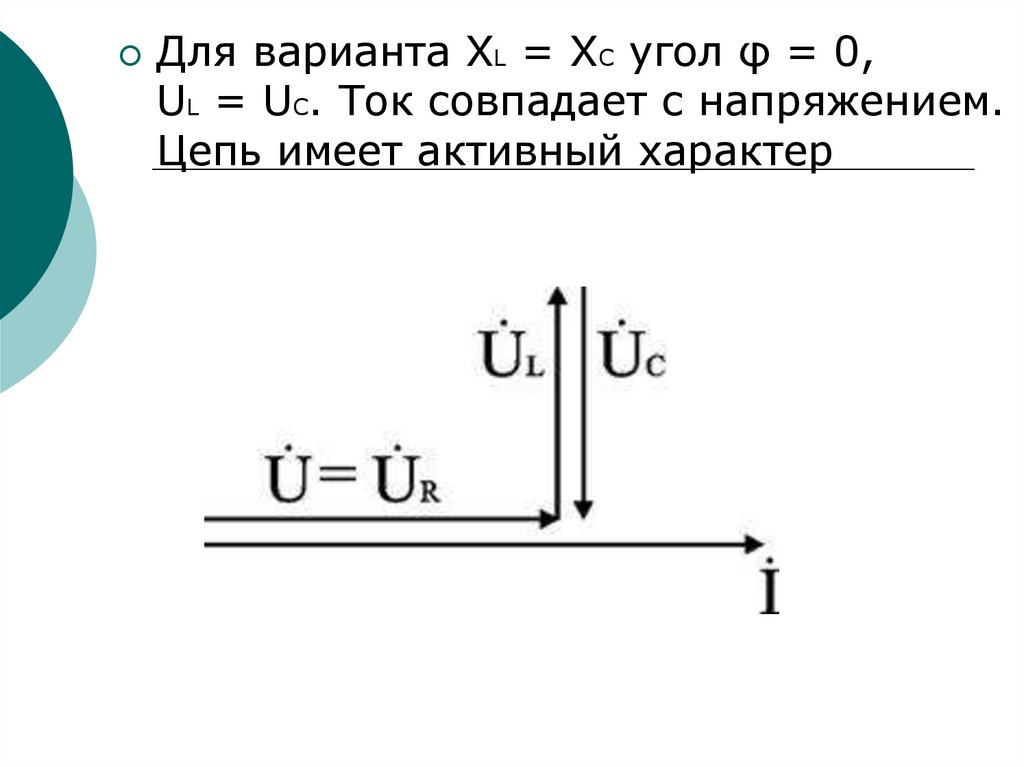
Для варианта XL = XC угол φ = 0,UL = UC. Ток совпадает с напряжением.
Цепь имеет активный характер
78.
Полное сопротивление. Полным сопротивлениемцепи называют величину
Из этого соотношения следует, что сопротивления Z, R
и X образуют треугольник: Z – гипотенуза, R и X –
катеты. Для удобства в этом треугольнике
рассматривают угол φ, который определяют
уравнением
φ = arctg((XL - XC) / R),
и называют углом сдвига фаз. С учетом него можно
дать дополнительные связ
R = Z cos φ,
X = Z sin φ.
79. Мощности в цепях переменного тока
Элемент R (резистор)P = U I cos φ,
Величину Р равную произведению
действующих значений тока и
напряжения называют активной
мощностью. Единицей ее
измерения является Ватт (Вт).
80.
Элемент L (индуктивность)Для количественной оценки мощности в
индуктивности используют величину QL и
называют ее реактивной (индуктивной)
мощностью. Единицей ее измерения
является ВАр (вольт-ампер реактивный).
QL = UL I sin φ
81.
Элемент С (ёмкость)По аналогии с индуктивностью вводят
величину QC, которую называют
реактивной (емкостной) мощностью.
Единицей ее измерения также является
ВАр.
Qс = Uс I sin φ,
82.
Если в цепи присутствуют элементы R,L и С, то активная и реактивная
мощности определяются уравнениями
P = U I cos φ,
Q = QL - QC,
Q = U I sin φ,
где φ – угол сдвига фаз
83.
Полная мощность цепиС учетом уравнений P и Q
S=UI
Единицей измерения полной
мощности является ВА – вольт-ампер.
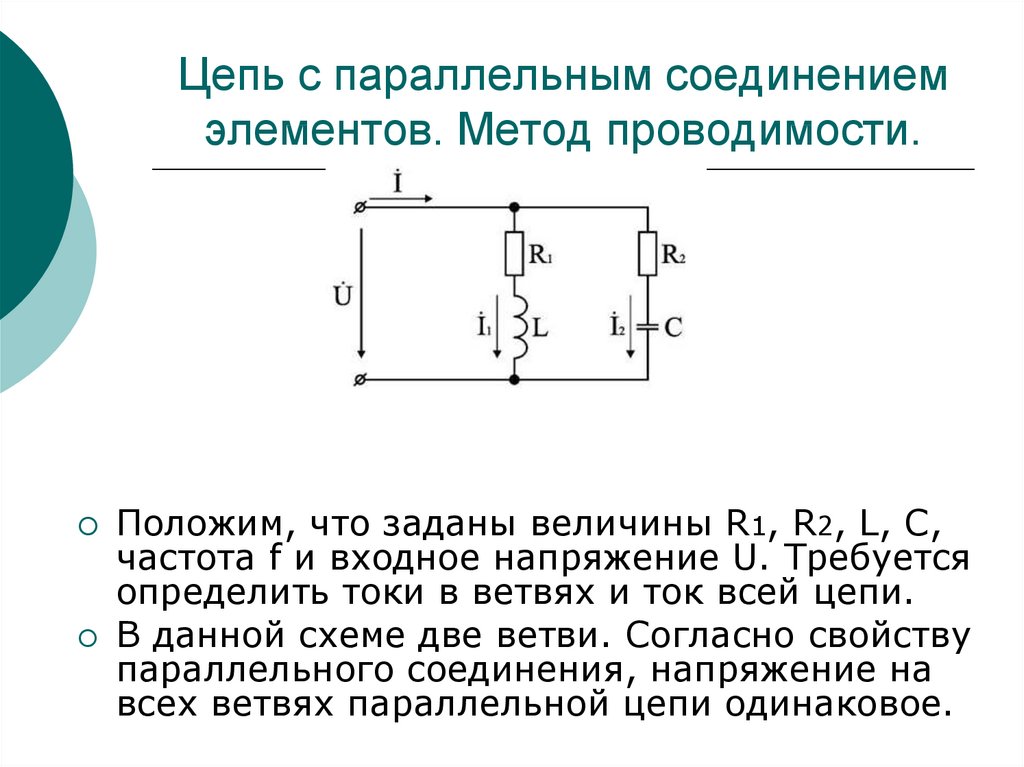
84. Цепь с параллельным соединением элементов. Метод проводимости.
Положим, что заданы величины R1, R2, L, С,частота f и входное напряжение U. Требуется
определить токи в ветвях и ток всей цепи.
В данной схеме две ветви. Согласно свойству
параллельного соединения, напряжение на
всех ветвях параллельной цепи одинаковое.
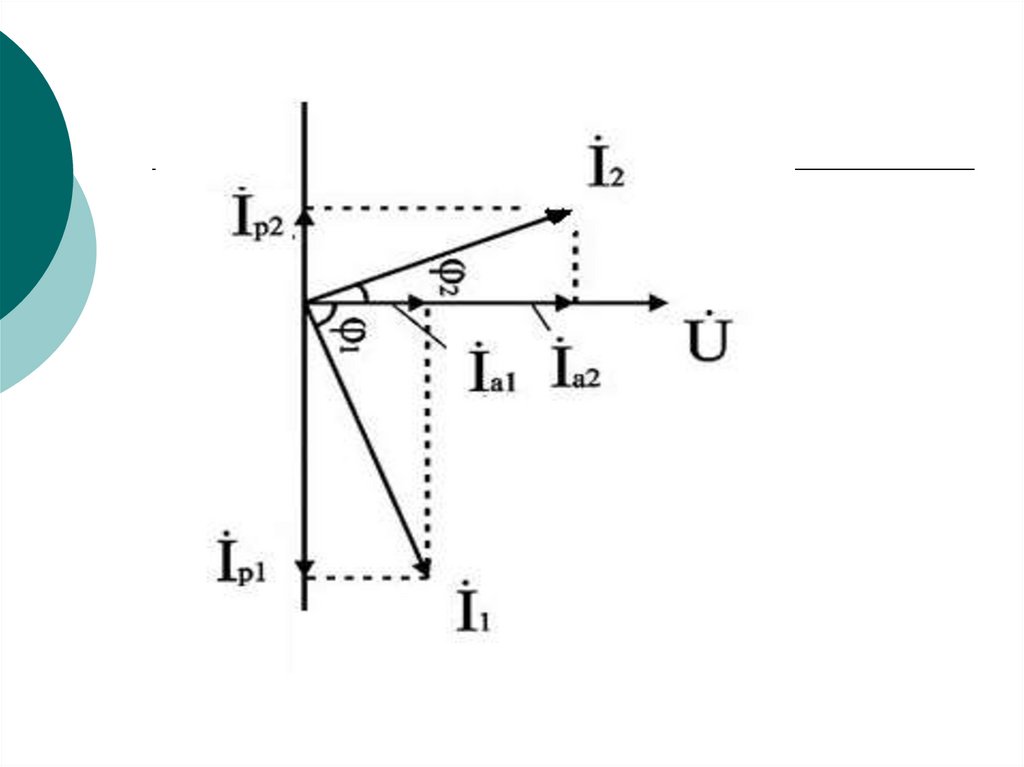
85.
Чаще всего используют методпроекций и метод проводимостей. В
методе проекций ток I1 и I2
раскладываются по две ортогональные
составляющие активную и
реактивную. Ось активной
составляющей совпадает с вектором
напряжения U. Ось реактивной
составляющей перпендикулярна
вектору U.
86.
87.
Активные составляющие токов равныI1а = I1 cos φ1, I2а = I2 cos φ2,
Iа = I1а + I2а.
Реактивные составляющие токов
равны
I1р = I1 sin φ1, I2р = I2 sin φ2,
Iр = I1р - I2р.
Полный ток находится из уравнений
,
φ = arctg(Iр / Iа).
88.
В методе проводимостей такжеиспользуется разложение на активные
и реактивные составляющие.
Активные составляющие токов
записываются в виде
где через g1 = R1 / Z12 обозначена величина,
названная активной проводимостью первой
ветви.
89.
Аналогичным образом получимгде g2 = R2 / Z22 обозначена величина,
названная активной проводимостью
второй ветви.
А величину g = g1 + g2 называют
активной проводимостью всей цепи.
90.
Реактивные составляющие токовгде b1 и b2 – реактивные проводимости
ветвей b1 = XL / Z12, b2 = XC / Z22.
Для реактивной проводимости всей
цепи имеем
b = b1 - b2.
91. Основы символического метода расчета цепей синусоидального тока
Расчет цепей переменного синусоидального тока может производитьсяне только путем построения векторных диаграмм, но и аналитически
– путем операций с комплексными числами, символически
изображающими синусоидальные ЭДС, напряжения и токи.
Достоинством векторных диаграмм является их наглядность,
недостатком – малая точность графических построений. Применение
символического метода позволяет производить расчеты цепей с
большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на
законах Кирхгофа и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме,
имеют совершенно такой же вид, как и соответствующие уравнения
для цепей постоянного тока. Только токи, ЭДС, напряжения и
сопротивления входят в уравнение в виде комплексных величин.
92. Закон Ома в комплексной форме
Под законом Ома в комплексной формепонимают:
Í=Ú/Z
93.
Комплексное сопротивление участкацепи представляет собой комплексное
число, вещественная часть которого
соответствует величине активного
сопротивления, а коэффициент при
мнимой части – реактивному
сопротивлению.
По виду записи комплексного
сопротивления можно судить о
характере участка цепи:
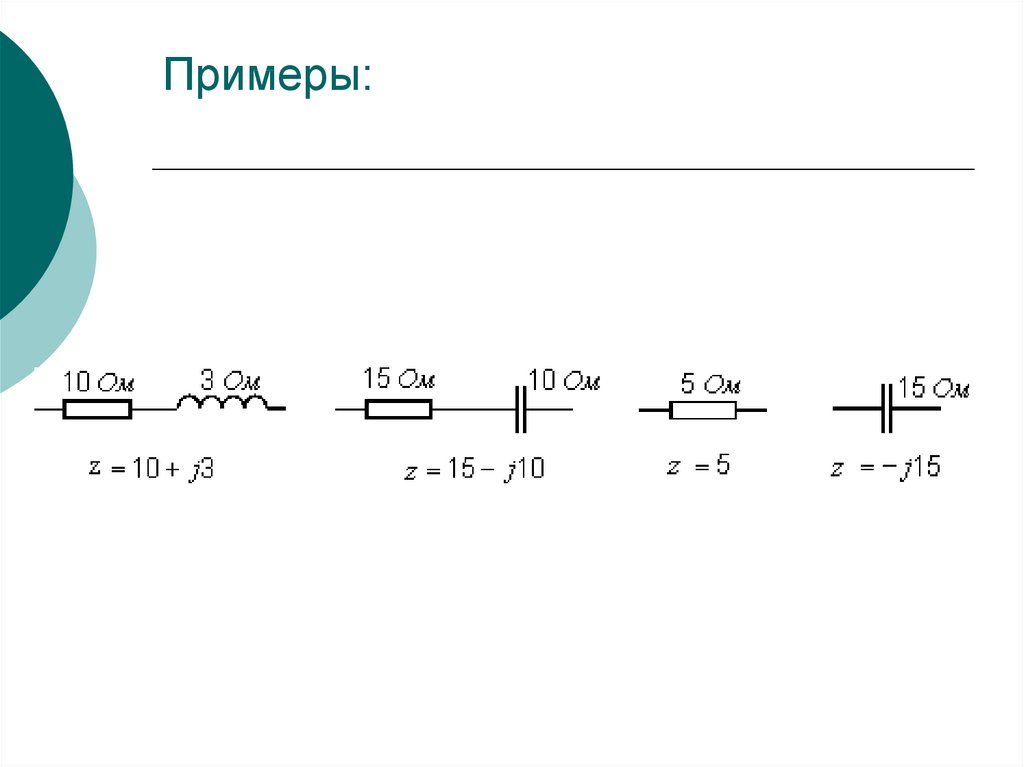
R + j X — активно-индуктивный
R – j X — активно-емкостный
94. Примеры:
95. Первый закон Кирхгофа в комплексной форме
Алгебраическая суммакомплексных действующих
значений токов в узле равна
нулю.
96. Второй закон Кирхгофа в комплексной форме
В замкнутом контуре электрическойцепи алгебраическая сумма
комплексных действующих значений
ЭДС равна алгебраической сумме
комплексных падений напряжений в
нём.
97. Мощность в комплексной форме
При использовании символическогометода можно пользоваться
понятиями мощностей. Но в
комплексной форме можно записать
только полную мощность:
где
— комплексно-сопряженный ток
S cos φ ± j S sin φ = P ± j Q.
98.
Полная мощность в комплекснойформе представляет собой
комплексное число, вещественная
часть которого соответствует
активной мощности
рассматриваемого участка, а
коэффициент при мнимой части –
реактивной мощности участка.
Значение знака перед мнимой
частью: “+” означает, что
напряжение опережает ток, нагрузка
– активно-индуктивная; “–” означает,
что нагрузка - активно-емкостная
99. Повышение коэффициента мощности в электрической цепи
Активная мощность потребителя определена формулойP = U I cos φ.
Величину cos φ здесь называют коэффициентом
мощности. Ток в линии питающей потребителя с
заданной мощностью Р равен
I = P / (U cos φ).
и будет тем больше, чем меньше cos φ. При этом
возрастают потери в питающей линии. Для их
снижения желательно увеличивать cos φ. Большинство
потребителей имеет активно-индуктивную нагрузку.
Увеличение cos φ возможно путем компенсации
индуктивной составляющей тока путем подключения
параллельно нагрузке конденсатора
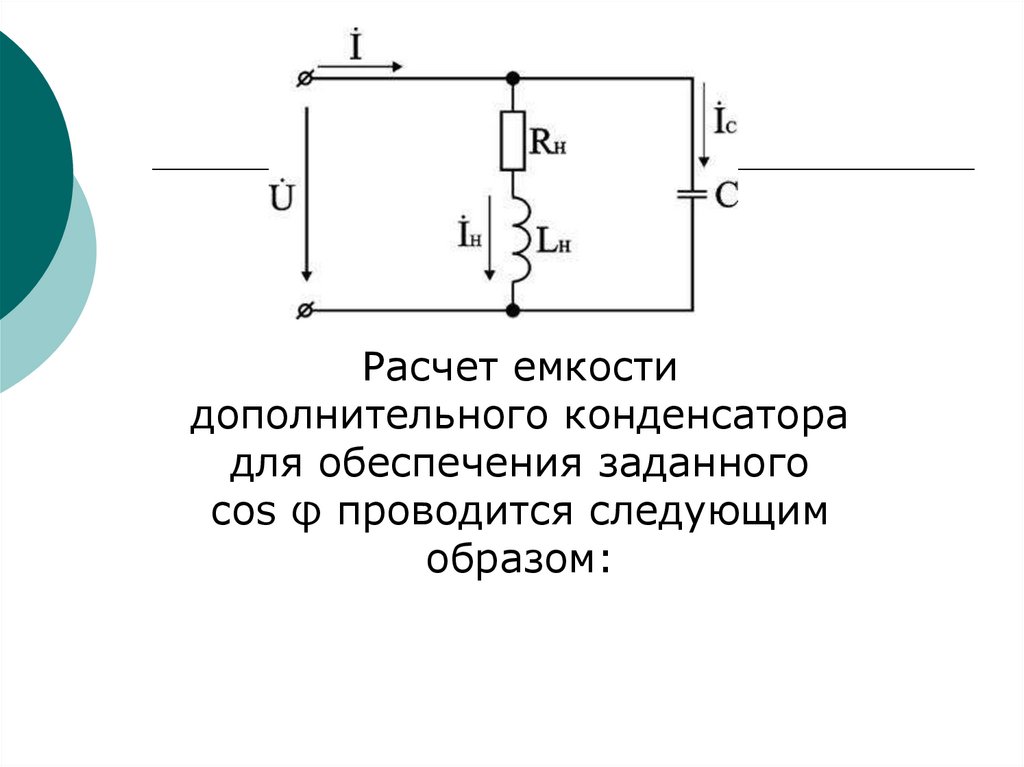
100.
Расчет емкостидополнительного конденсатора
для обеспечения заданного
cos φ проводится следующим
образом:
101.
Пусть известны параметры нагрузки Pн, U иIн . Можно определить cosφн
cos φн = P / (U Iн).
Подключение емкости не изменяет активную
составляющую нагрузки
Iна = Iн cos φн = Pн / U
Реактивная составляющая нагрузки Iнр может
быть выражена через tg φн
Iнр = Iна tg φн.
При подключении емкости величина Iнр
уменьшается на величину IC.
Если задано, что коэффициент мощности в
питающей линии должен быть равен cos φ,
то можно определить величину реактивной
составляющей тока в линии
Iр = Iа tg φ.
102.
Уменьшение реактивной составляющейнагрузки с Iнр до Iр определяет величину тока
компенсирующей емкости
IC = Iнр - Iр = Iа (tg φн - tg φ).
Подставляя в уравнение, значение Iна и
учитывая, что IC = U / XC = U ωC, получим
U ωC = Pн / U · (tg φн - tg φ), откуда для
емкости конденсатора имеем
2
C = Pн / ωU · (tg φн - tg φ).
Для больших значений Pн величина емкости C
может оказаться слишком большой, что
технически трудно реализовать. В этом
случае используют синхронные
компенсирующие машины.
103. Резонансы в цепях синусоидального тока.
Резонансом называется такойрежим работы цепи, включающей
в себя индуктивные и емкостные
элементы, при котором ток на
входе цепи совпадает по фазе с
входным напряжением
104. Резонанс в цепи с последовательно соединенными элементами (резонанс напряжений)
Условие резонанса напряжений:105.
При этом следует:Режима резонанса можно добиться
путем изменения параметров L и C, а
также частоты. Для резонансной
частоты можно записать
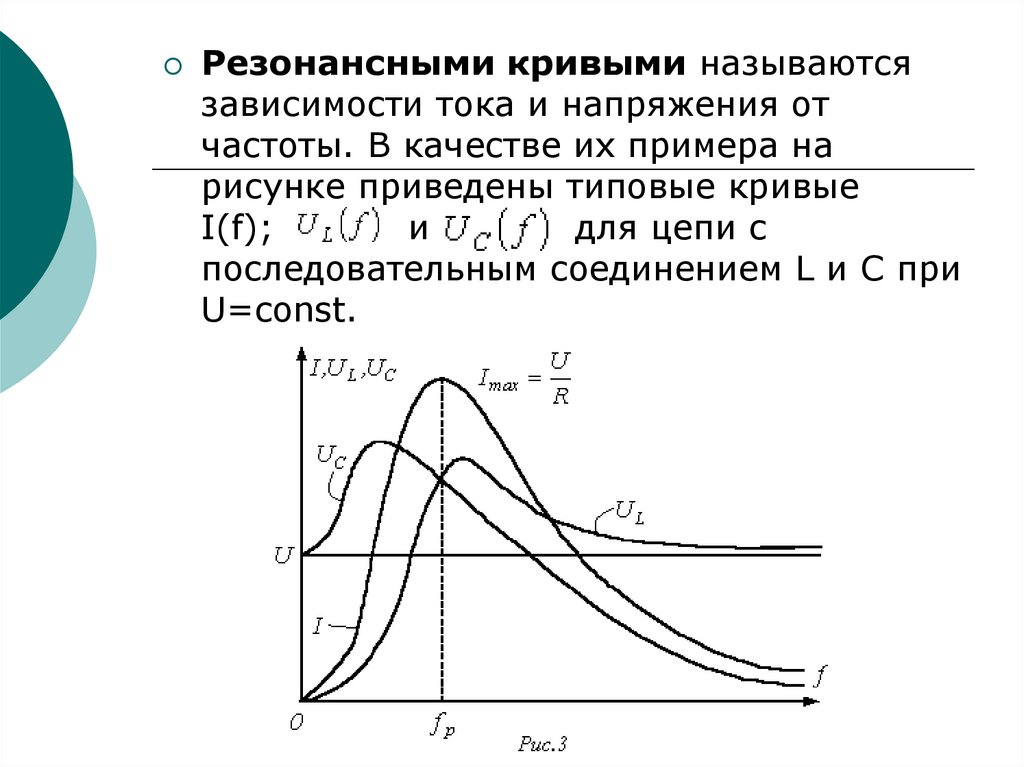
106.
Резонансными кривыми называютсязависимости тока и напряжения от
частоты. В качестве их примера на
рисунке приведены типовые кривые
I(f);
и
для цепи с
последовательным соединением L и C при
U=const.
107.
Важной характеристикой резонансного контураявляется добротность Q, определяемая
отношением напряжения на индуктивном
(емкостном) элементе к входному напряжению:
Другим параметром резонансного контура
является характеристическое
сопротивление, связанное с добротностью
соотношением
или
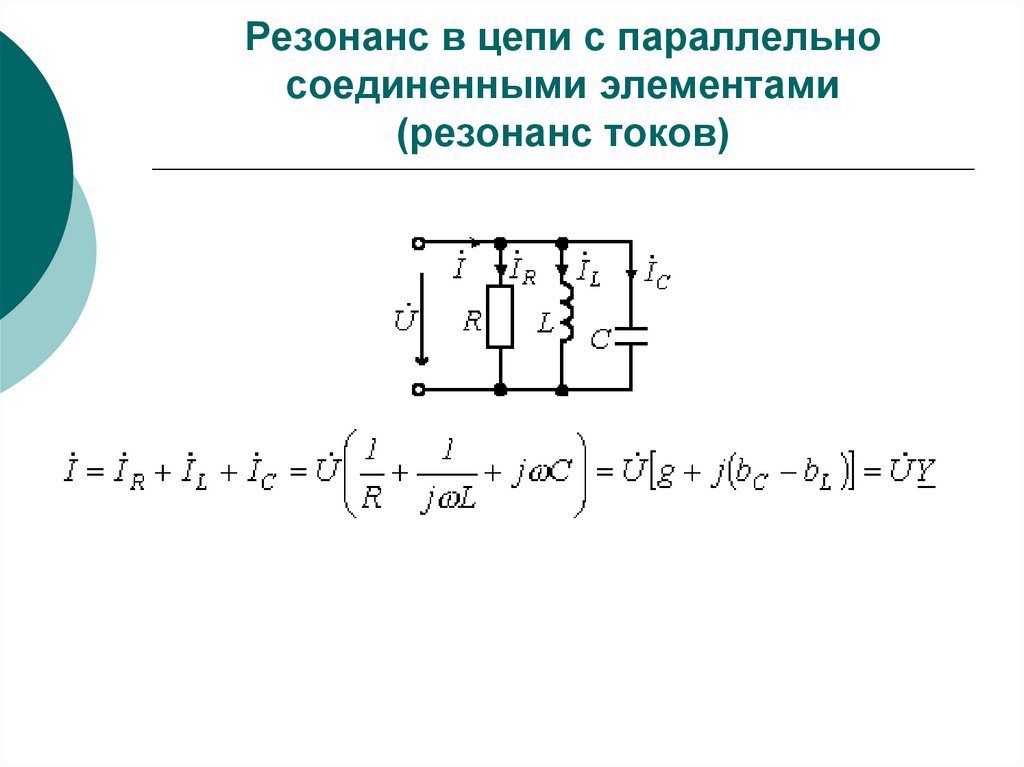
108. Резонанс в цепи с параллельно соединенными элементами (резонанс токов)
109.
Условие резонанса токовили
При этом
Таким образом, при резонансе токов
входная проводимость цепи минимальна,
а входное сопротивление, наоборот,
максимально.
110. Трехфазные электрические цепи Основные понятия и определения
Трехфазнаяцепь
является
частным
случаем многофазных систем электрических
цепей, представляющих собой совокупность
электрических цепей, в которых действуют
синусоидальные ЭДС одинаковой частоты,
отличающиеся по фазе одна от другой и
создаваемые общим источником энергии.
Каждую из частей многофазной системы,
характеризующуюся
одинаковым
током,
принято называть фазой. Таким образом,
понятие "фаза" имеет два значения: первое –
аргумент
синусоидально
изменяющейся
величины, второе – часть многофазной
системы электрических цепей.
111.
Трехфазныецепи
–
наиболее
распространенные
в
современной
электроэнергетике. Это объясняется рядом
их
преимуществ
по
сравнению
с
однофазными:
- экономичность производства и передачи
энергии по сравнению с однофазными
цепями;
возможность
сравнительно
простого
получения
кругового
вращающегося
магнитного
поля,
необходимого
для
трехфазного асинхронного двигателя;
возможность
получения
в
одной
установке
двух
эксплуатационных
напряжений – фазного и линейного.
112.
Большойвклад
в
разработку
трехфазных систем внес выдающийся
русский
ученый-электротехник
М.О.Доливо-Добровольский в 1891 г,
создавший трехфазные асинхронные
двигатели,
трансформаторы,
предложивший
трехи
четырехпроводные цепи, в связи с чем
по
праву
считающийся
основоположником трехфазных систем.
113.
Трехфазная цепь состоит из трехосновных элементов:
- трехфазного генератора, в котором
механическая энергия преобразуется в
электрическую с трехфазной системой
ЭДС;
- линии передачи со всем необходимым
оборудованием;
- приемников (потребителей), которые
могут быть как трехфазными (например,
трехфазные асинхронные двигатели),
так и однофазными (например, лампы
накаливания).
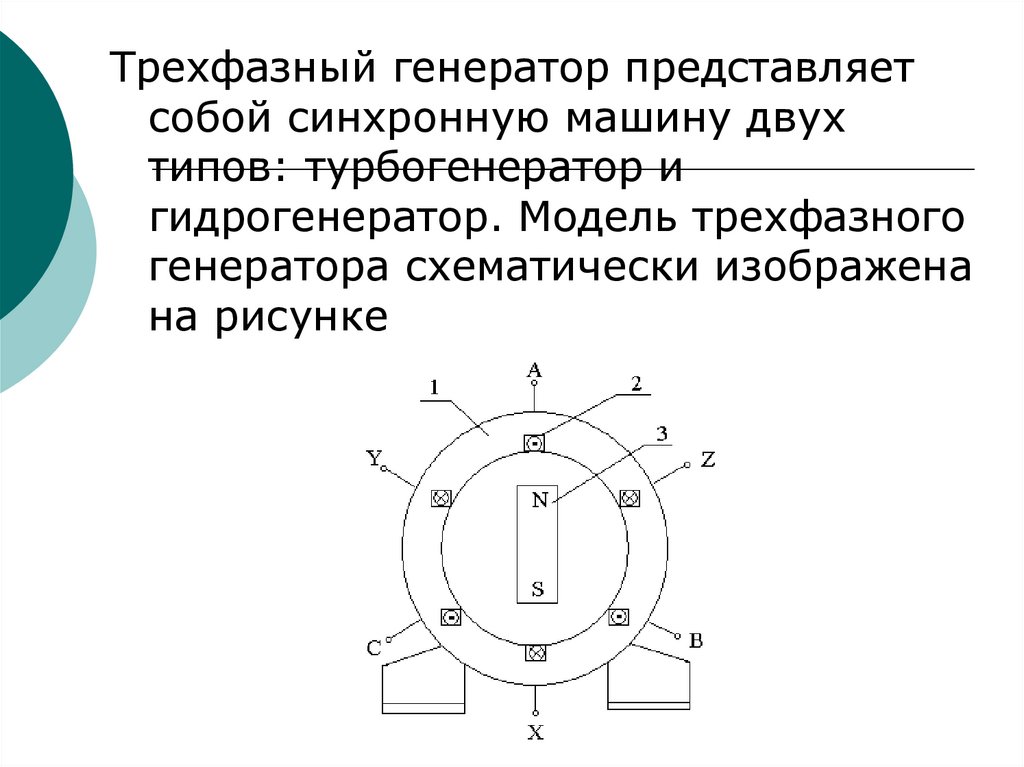
114.
Трехфазный генератор представляетсобой синхронную машину двух
типов: турбогенератор и
гидрогенератор. Модель трехфазного
генератора схематически изображена
на рисунке
115.
На статоре 1 генератора размещаетсяобмотка 2, состоящая из трех частей или, как
их принято называть, фаз. Обмотки фаз
располагаются на статоре таким образом,
чтобы их магнитные оси были сдвинуты в
пространстве относительно друг друга на
угол 2π/3, т.е. на 120°.
На рисунке каждая фаза обмотки статора
условно показана состоящей из одного витка.
Начала фаз обозначены буквами A, B и C, а
концы – X, Y, Z. Ротор 3 представляет собой
электромагнит, возбуждаемый постоянным
током обмотки возбуждения, расположенной
на роторе
116.
При вращении ротора турбиной сравномерной скоростью в обмотках
фаз статора индуктируются
периодически изменяющиеся
синусоидальные ЭДС одинаковой
частоты и амплитуды, но
отличающиеся друг от друга по фазе
на 120° вследствие их
пространственного смещения.
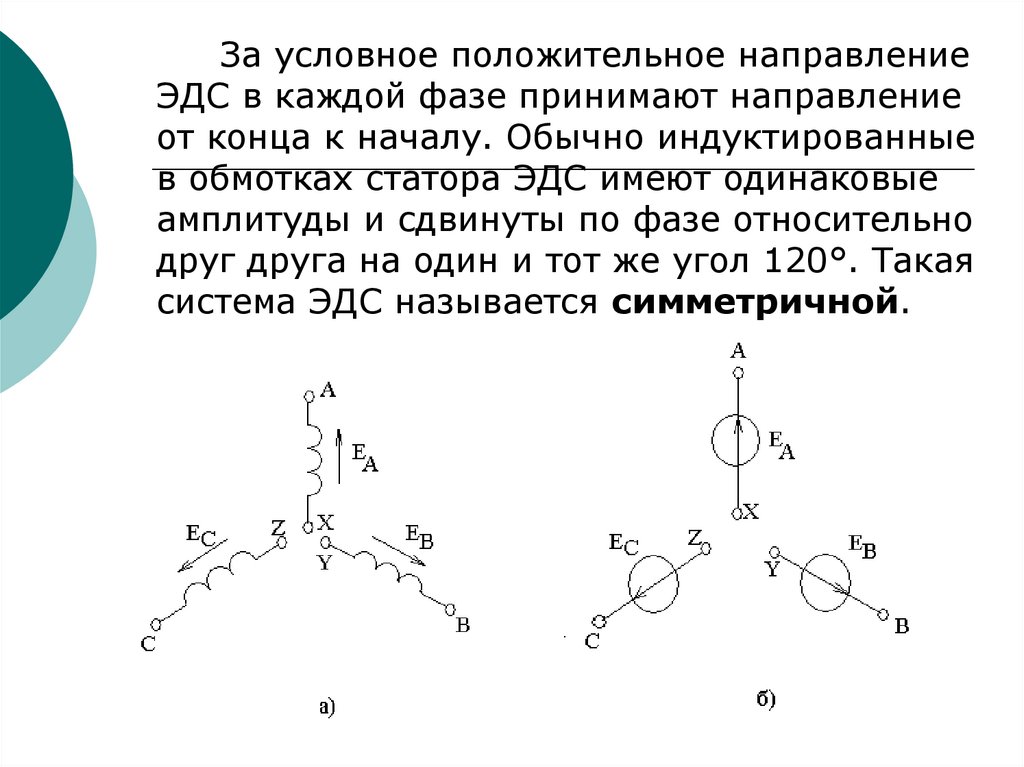
117.
За условное положительное направлениеЭДС в каждой фазе принимают направление
от конца к началу. Обычно индуктированные
в обмотках статора ЭДС имеют одинаковые
амплитуды и сдвинуты по фазе относительно
друг друга на один и тот же угол 120°. Такая
система ЭДС называется симметричной.
118. Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями
комплексногопеременного.
119.
Если ЭДС одной фазы (например,фазы А) принять за исходную и
считать её начальную фазу равной
нулю, то выражения мгновенных
значений ЭДС можно записать в виде
eA = Em sin ωt,
eB = Em sin (ωt - 120°),
eC = Em sin (ωt - 240°)=
= Em sin (ωt + 120°).
120. График мгновенных значений ЭДС
121.
Комплексные действующие ЭДСбудут иметь выражения:
ĖA = Em ej0°
ĖB = Em e-j120°
ĖC = Em ej120°
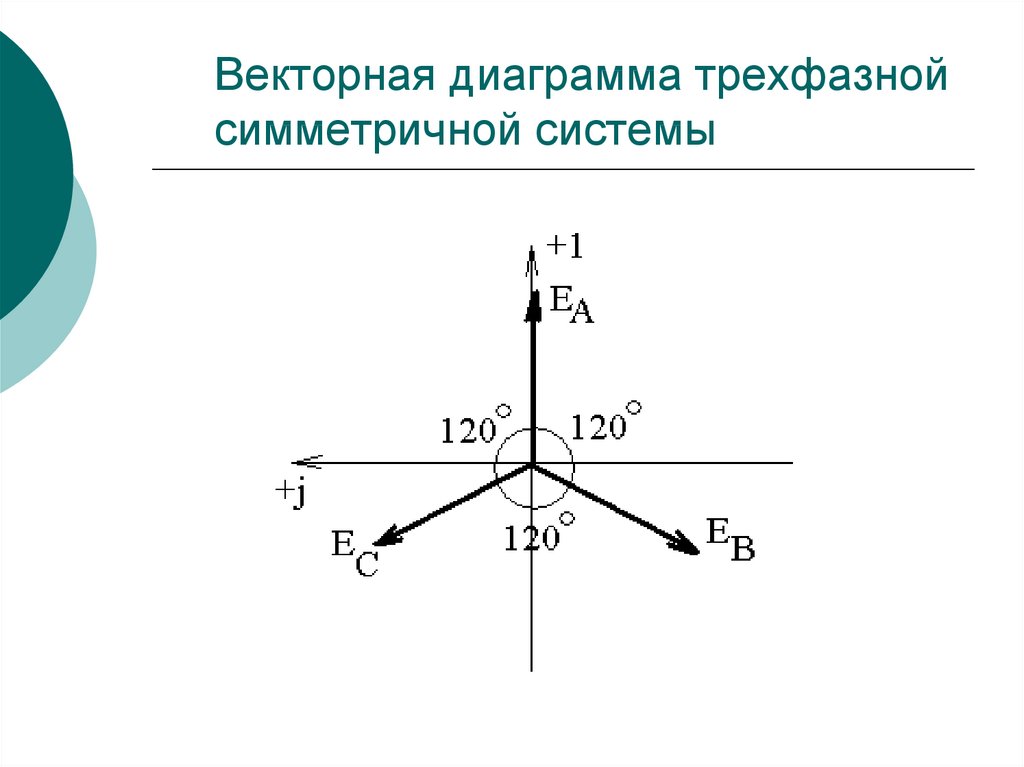
122. Векторная диаграмма трехфазной симметричной системы
123.
Систему ЭДС, в которой ЭДС фазы Вотстает по фазе от ЭДС фазы А, а ЭДС
фазы С по фазе – от ЭДС фазы В,
называют
системой
прямой
последовательности. Если изменить
направление
вращения
ротора
генератора, то последовательность фаз
изменится и будет называться обратной.
Последовательность фаз определяет
направление
вращения
трехфазных
двигателей.
Для
определения
последовательности
фаз
имеются
специальные приборы – фазоуказатели.
124.
125.
В период зарождения трехфазныхсистем имелись попытки использовать
несвязанную систему, в которой фазы
обмотки
генератора
не
были
электрически соединены между собой и
каждая фаза соединялась со своим
приемником двумя проводами. Такие
системы
не
получили
применения
вследствие их неэкономичности: для
соединения генератора с приемником
требовалось шесть проводов.
126.
127.
Более совершенными и экономичнымиявляются связанные цепи, в которых фазы
обмотки электрически соединены между
собой. Существуют различные способы
соединения фаз трехфазных источников
питания
и
трехфазных
потребителей
электроэнергии.
Наиболее распространенными являются
соединения "звезда" и "треугольник". При
этом способ соединения фаз источников и
фаз потребителей в трехфазных системах
могут быть различными. Фазы источника
обычно
соединены
"звездой",
фазы
потребителей соединяются либо "звездой",
либо "треугольником".
128. Соединение фаз генератора и приемника звездой
При соединение фаз обмотки генератора(или трансформатора) звездой их концы
X, Y и Z соединяют в одну общую точку
N, называемую нейтральной точкой (или
нейтралью). Концы фаз приемников (Za,
Zb, Zc) также соединяют в одну точку n.
Такое
соединение
называется
соединение звезда
129.
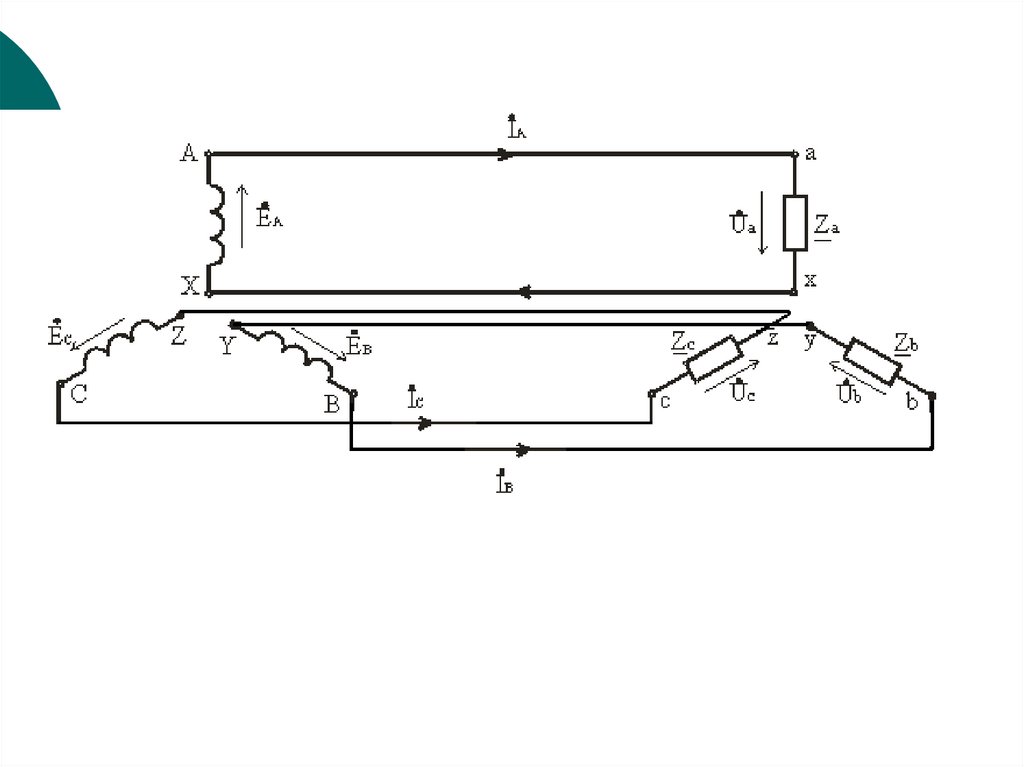
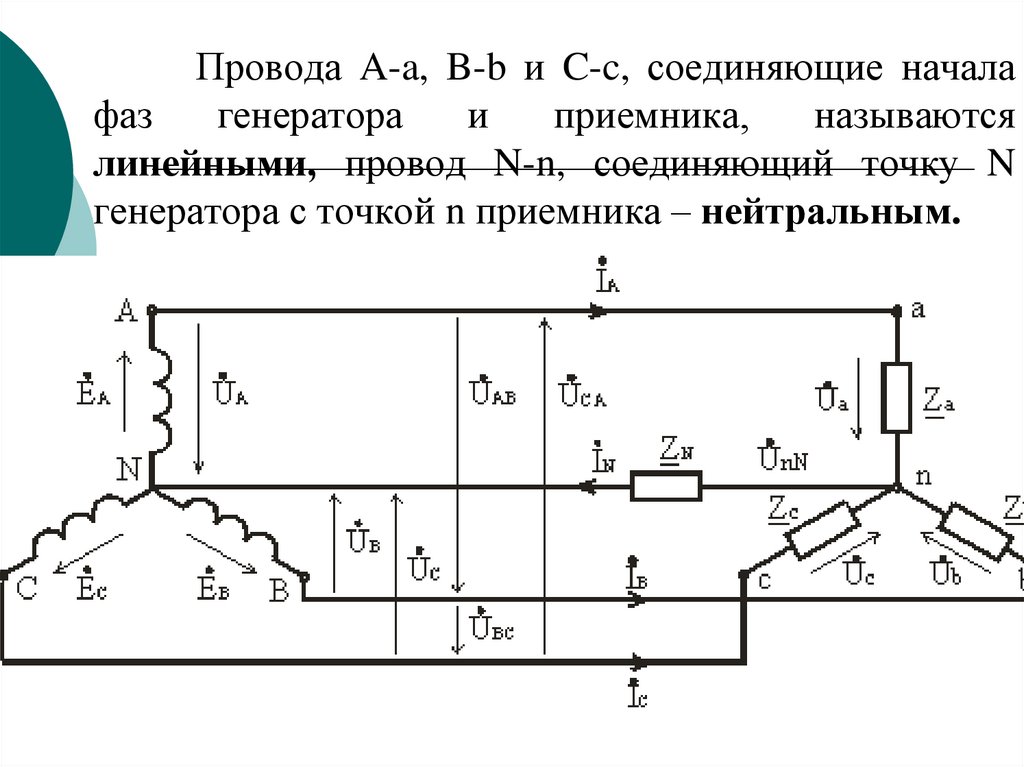
130. Провода A-a, B-b и C-c, соединяющие начала фаз генератора и приемника, называются линейными, провод N-n, соединяющий точку N
генератора с точкой n приемника – нейтральным.131.
Трехфазная цепь с нейтральным проводом будетчетырехпроводной, без нейтрального провода –
трехпроводной.
В трехфазных цепях различают фазные и линейные
напряжения.
Фазное напряжение UФ – напряжение между началом и
концом фазы или между линейным проводом и нейтралью
(UA, UB, UC у источника; Ua, Ub, Uc у приемника). За
условно положительные направления фазных напряжений
принимают направления от начала к концу фаз.
Линейное напряжение (UЛ) – напряжение между линейными
проводами или между одноименными выводами разных
фаз (UAB, UBC, UCA). Условно положительные направления
линейных напряжений приняты от точек, соответствующих
первому индексу, к точкам соответствующим второму
индексу.
132.
По аналогии с фазными и линейными напряжениямиразличают также фазные и линейные токи:
Фазные (IФ) – это токи в фазах генератора и
приемников.
Линейные (IЛ) – токи в линейных проводах.
При соединении в звезду фазные и линейные токи
равны
IФ = I Л
По первому закону Кирхгофа ток в нейтральном проводе в
комплексной форме
İN = İA + İB + İC.
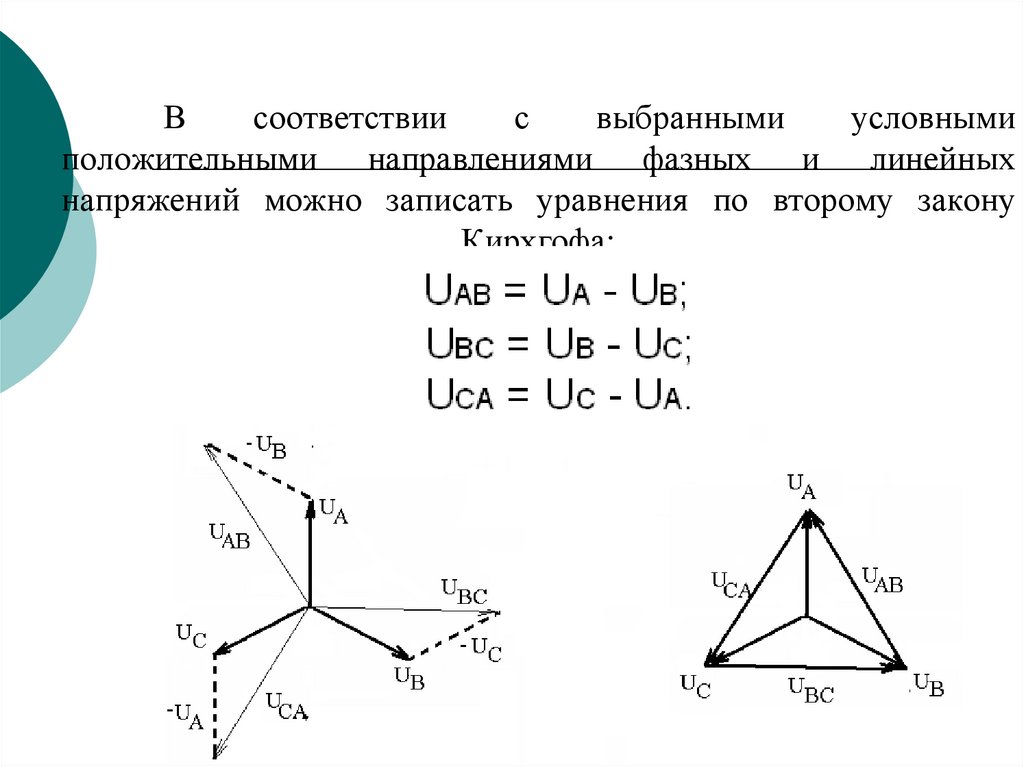
133. В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по
второму законуКирхгофа:
134.
Действующие значения линейных напряжений можноопределить графически по векторной диаграмме или по
треугольнику, образованному векторами двух фазных и
одного линейного напряжений:
UЛ = 2 UФ cos 30°
или
UЛ = √3 UФ
Предусмотренные ГОСТом линейные и фазные
напряжения для цепей низкого напряжения связаны между
собой соотношениями:
UЛ = 660 В; UФ = 380 В;
UЛ = 380 В; UФ = 220 В;
UЛ = 220 В; UФ = 127 В.
135. Классификация приемников в трехфазной цепи
Приемники, включаемые в трехфазную цепь, могут бытьлибо однофазными, либо трехфазными. К однофазным
приемникам относятся электрические лампы накаливания и
другие осветительные приборы, различные бытовые приборы,
однофазные двигатели и т.д. К трехфазным приемникам
относятся трехфазные асинхронные двигатели и индукционные
печи. Обычно комплексные сопротивления фаз трехфазных
приемников равны между собой:
Za = Zb = Zc = Zejφ.
Такие приемники называют симметричными. Если это условие
не выполняется, то приемники называют несимметричными.
При этом, если Za = Zb = Zc, то трехфазный приемник называют
равномерным, если φa = φb = φc, то однородным.
136. Четырехпроводная цепь
Для расчета трехфазной цепи применимы методы,используемые
для
расчета
линейных
цепей.
Обычно
сопротивления проводов и внутреннее сопротивление генератора
меньше сопротивлений приемников, поэтому для упрощения
расчетов таких цепей (если не требуется большая точность)
сопротивления проводов можно не учитывать (ZЛ = 0, ZN = 0).
Тогда фазные напряжения приемника Ua, Ub и Uc будут равны
соответственно фазным напряжениям источника электрической
энергии (генератора или вторичной обмотки трансформатора), т.е.
Ua = UA; Ub = UB; Uc = UC. Если полные комплексные
сопротивления фаз приемника равны Za = Zb = Zc, то токи в
каждой фазе можно определить по формулам
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
В соответствии с первым законом Кирхгофа ток в нейтральном
проводе
İN = İa + İb + İc = İA + İB + İC.
137. Симметричная нагрузка приемника
Присимметричной
системе
напряжений
и
симметричной нагрузке, когда Za = Zb = Zc, т.е. когда
Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по
значению и углы сдвига фаз одинаковы
Ia = Ib = Ic = Iф = Uф / Zф,
φa = φb = φc = φ = arctg (Xф/Rф).
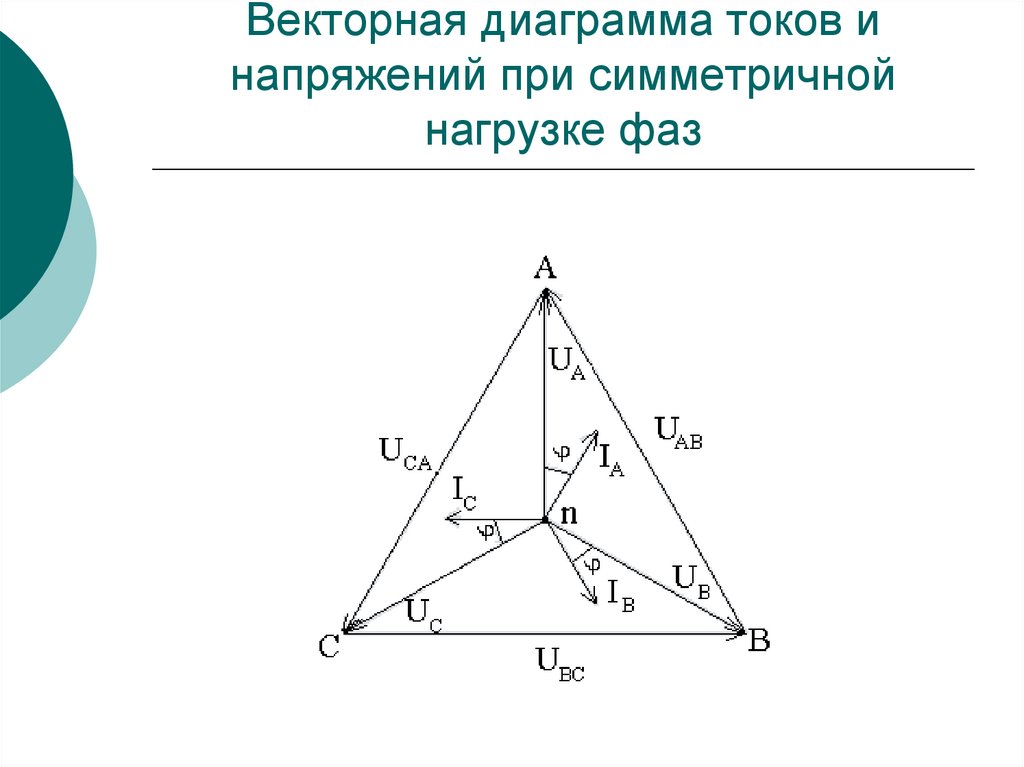
Построив векторную диаграмму токов для симметричного
приемника, легко установить, что геометрическая сумма трех
векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в
случае симметричной нагрузки ток в нейтральном проводе
IN = 0, поэтому необходимость в нейтральном проводе
отпадает.
138. Векторная диаграмма токов и напряжений при симметричной нагрузке фаз
139. Несимметричная нагрузка приемника
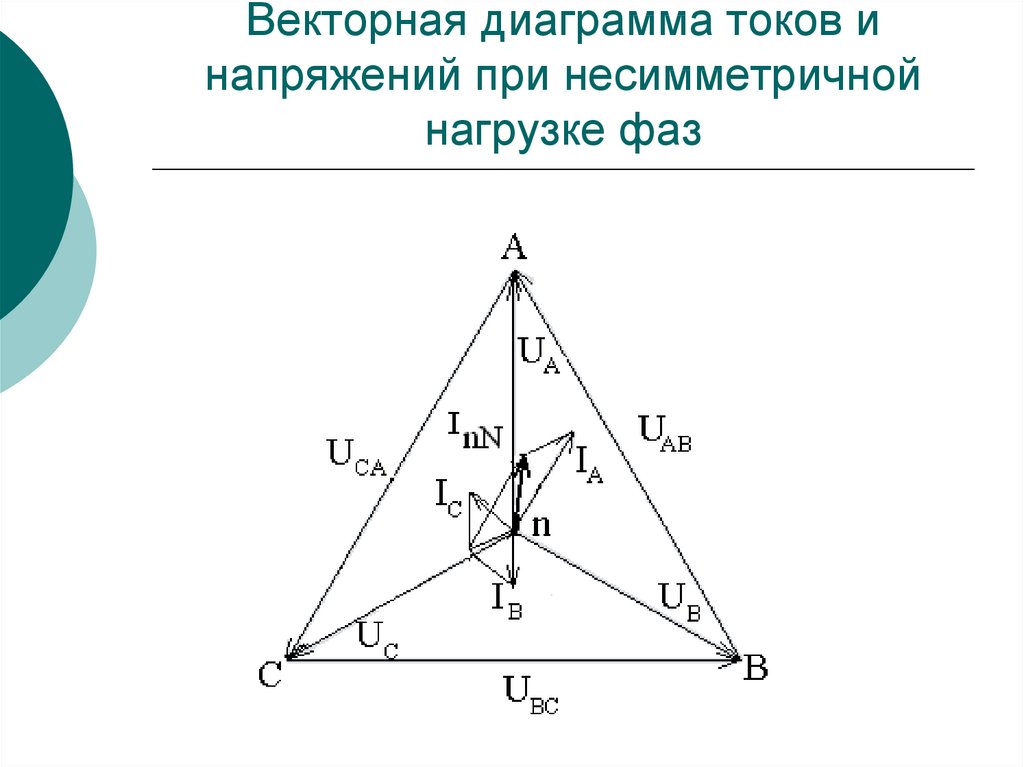
При симметричной системе напряжений и несимметричнойнагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах
потребителя различны и определяются по закону Ома
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
Ток в нейтральном проводе İN равен геометрической сумме
фазных токов
İN = İa + İb + İc.
Напряжения будут Ua = UA; Ub = UB; Uc = UC, UФ = UЛ/√3 ,
благодаря нейтральному проводу при ZN = 0.
Следовательно, нейтральный провод обеспечивает симметрию
фазных напряжений приемника при несимметричной
нагрузке.
Поэтому в четырехпроводную сеть включают однофазные
несимметричные нагрузки, например, электрические лампы
накаливания. Режим работы каждой фазы нагрузки,
находящейся под неизменным фазным напряжением
генератора, не будет зависеть от режима работы других фаз.
140. Векторная диаграмма токов и напряжений при несимметричной нагрузке фаз
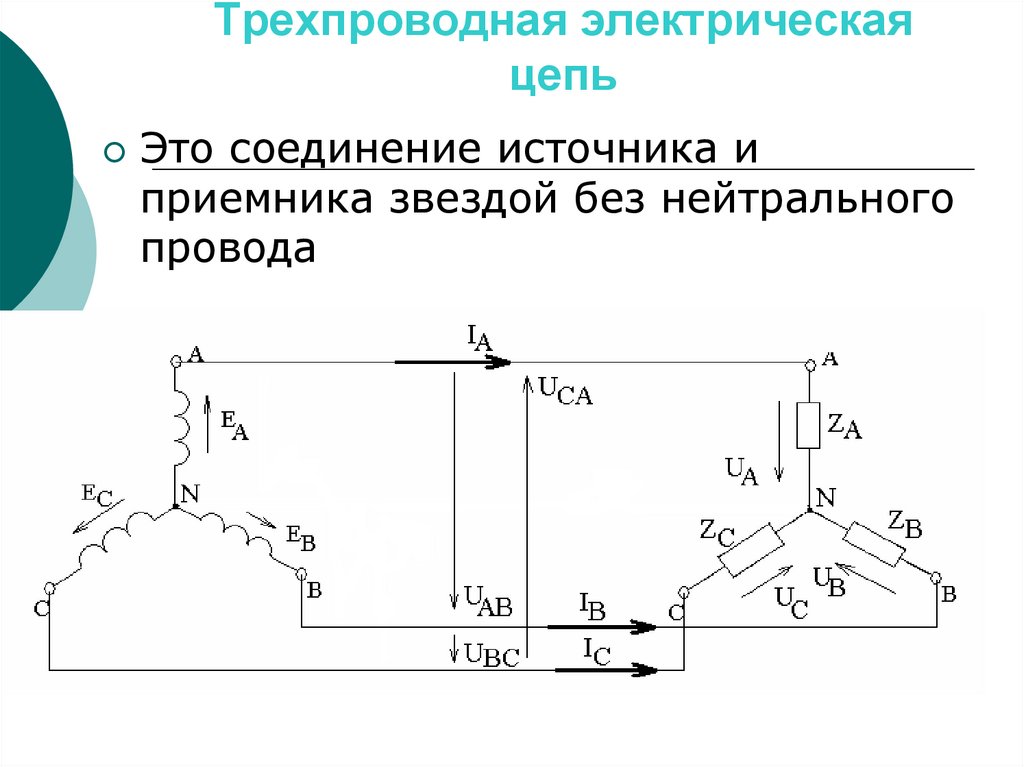
141. Трехпроводная электрическая цепь
Это соединение источника иприемника звездой без нейтрального
провода
142.
При симметричной нагрузке, когдаZa = Zb = Zc = Z, напряжение между
нейтральной точкой источника N и
нейтральной точкой приемника n
равно нулю, UnN = 0.
При несимметричной нагрузке
Za ≠ Zb ≠ Zc между нейтральными
точками приемника и источника
электроэнергии возникает
напряжение смещения нейтрали UnN
143.
Для определения напряжениясмещения нейтрали можно
воспользоваться формулой
межузлового напряжения
Тогда напряжения по фазам
Зная фазные напряжения приемника, можно
определить фазные токи:
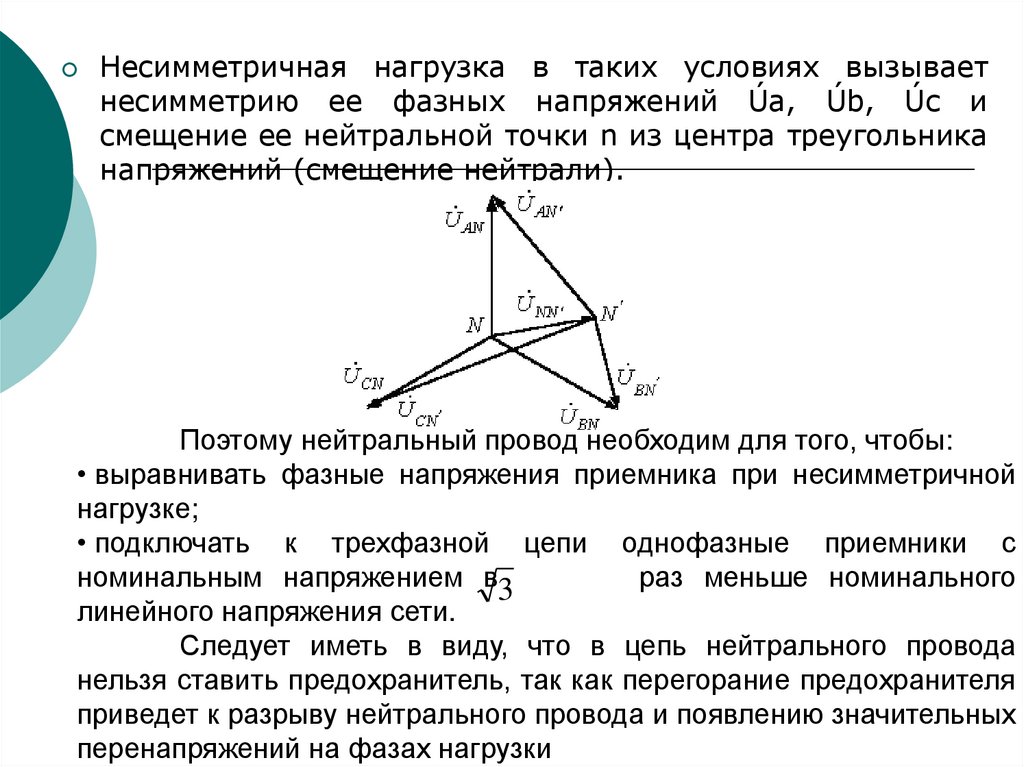
144.
Несимметричная нагрузка в таких условиях вызываетнесимметрию ее фазных напряжений Úa, Úb, Úc и
смещение ее нейтральной точки n из центра треугольника
напряжений (смещение нейтрали).
Поэтому нейтральный провод необходим для того, чтобы:
• выравнивать фазные напряжения приемника при несимметричной
нагрузке;
• подключать к трехфазной цепи однофазные приемники с
номинальным напряжением в3
раз меньше номинального
линейного напряжения сети.
Следует иметь в виду, что в цепь нейтрального провода
нельзя ставить предохранитель, так как перегорание предохранителя
приведет к разрыву нейтрального провода и появлению значительных
перенапряжений на фазах нагрузки
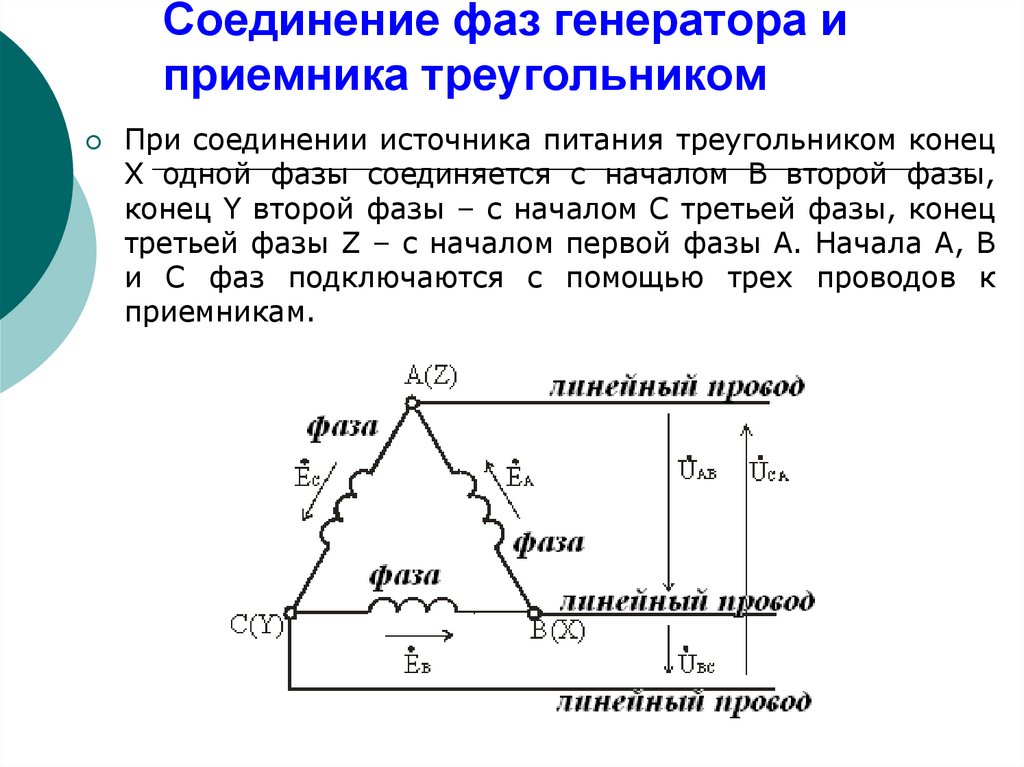
145. Соединение фаз генератора и приемника треугольником
При соединении источника питания треугольником конецX одной фазы соединяется с началом В второй фазы,
конец Y второй фазы – с началом С третьей фазы, конец
третьей фазы Z – c началом первой фазы А. Начала А, В
и С фаз подключаются с помощью трех проводов к
приемникам.
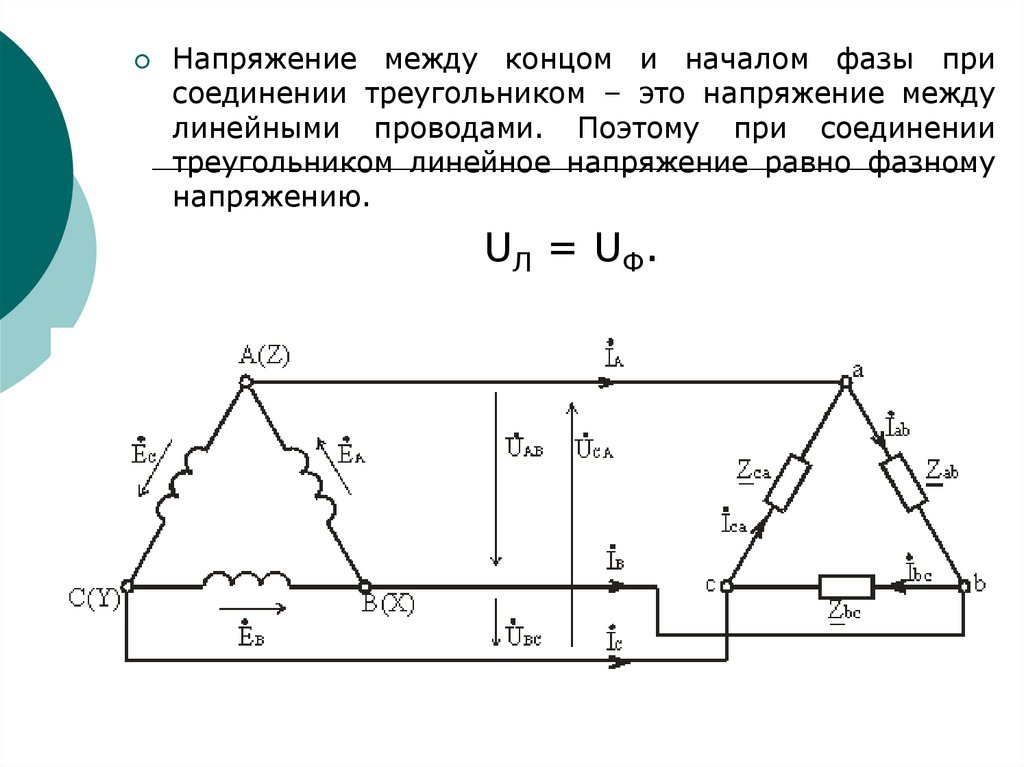
146.
Напряжение между концом и началом фазы присоединении треугольником – это напряжение между
линейными проводами. Поэтому при соединении
треугольником линейное напряжение равно фазному
напряжению.
UЛ = UФ.
147.
Пренебрегая сопротивлением линейныхпроводов,
линейные
напряжения
потребителя можно приравнять к линейным
напряжениям источника питания: Uab = UAB,
Ubc = UBC, Uca = UCA.
По фазам Zab, Zbc, Zca приемника
протекают фазные токи İab, İbc и İca.
Условное
положительное
направление
фазных напряжений Úab, Úbc и Úca
совпадает с положительным направлением
фазных токов. Условное положительное
направление линейных токов İA, İB и İC
принято
от
источников
питания
к
приемнику.
148.
В отличие от соединения звездой присоединении треугольником фазные токи не
равны линейным. Токи в фазах приемника
определяются по формулам
İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.
Линейные токи можно определить по
фазным, составив уравнения по первому
закону Кирхгофа для узлов a, b и c
İA = İab - İca; İB = İbc - İab; İC = İca - İbc.
Следовательно
Iл = √3IФ
149. Симметричная нагрузка приемника
При симметричной нагрузкеZab = Zbc = Zca = Zejφ,
т.е. Zab = Zbc = Zca = Z, φab = φbc = φca = φ.
Так как линейные (они же фазные) напряжения
UAB, UBC, UCA симметричны, то и фазные токи
образуют симметричную систему
İab = Úab / Zab; İbc = Úbc / Zbc;
İca = Úca / Zca.
Абсолютные значения их равны, а сдвиги по фазе
относительно друг друга составляют 120°.
Линейные токи
İA = İab - İca; İB = İbc - İab; İC = İca - İbc;
образуют также симметричную систему токов
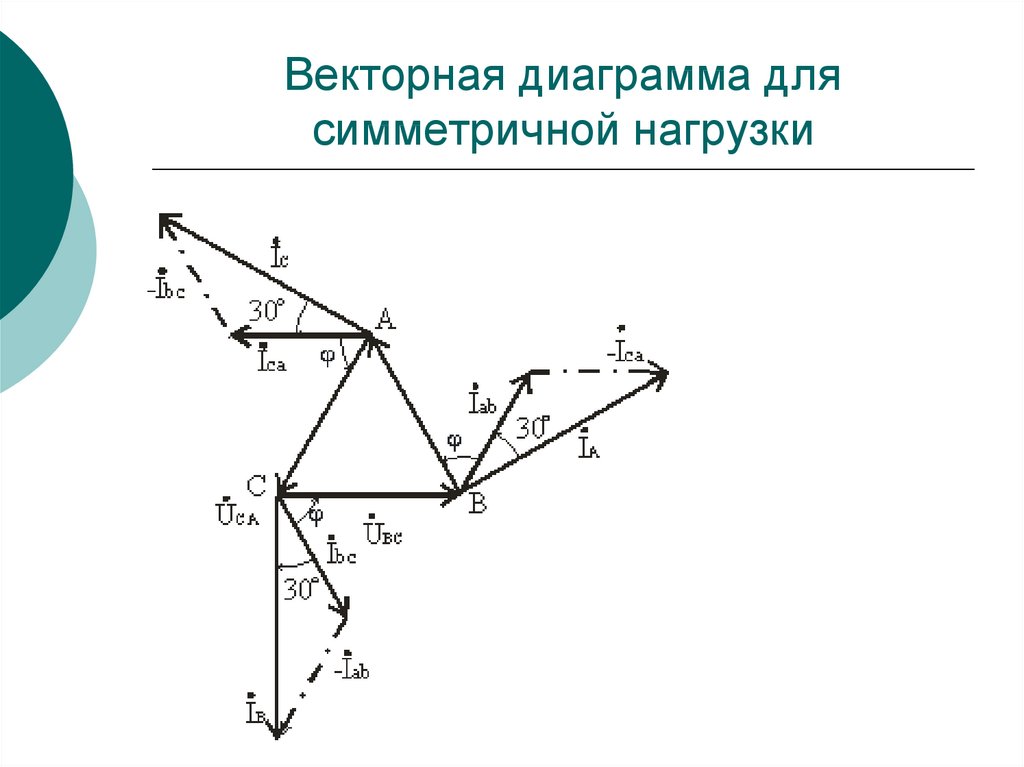
150. Векторная диаграмма для симметричной нагрузки
151.
На векторной диаграмме фазные токиотстают от фазных напряжений на угол φ
(полагаем, что нагрузка фаз приемника
является активно-индуктивной, т.е. φ > 0°).
Из диаграммы следует, что любой линейный
ток больше фазного в
раз. Линейный ток İA
отстает по фазе от фазного тока İab на угол
30°, на этот же угол отстает İB от İbc, İC от
İca.
Таким
образом,
при
соединении
треугольником
действующее
значение
линейного тока при симметричной нагрузке в
раз
больше
действующего
значения
фазного тока и UЛ = UФ; IЛ =
IФ.
При равномерной нагрузке фаз расчет
трехфазной цепи соединенной треугольником,
можно свести к расчету одной фазы.
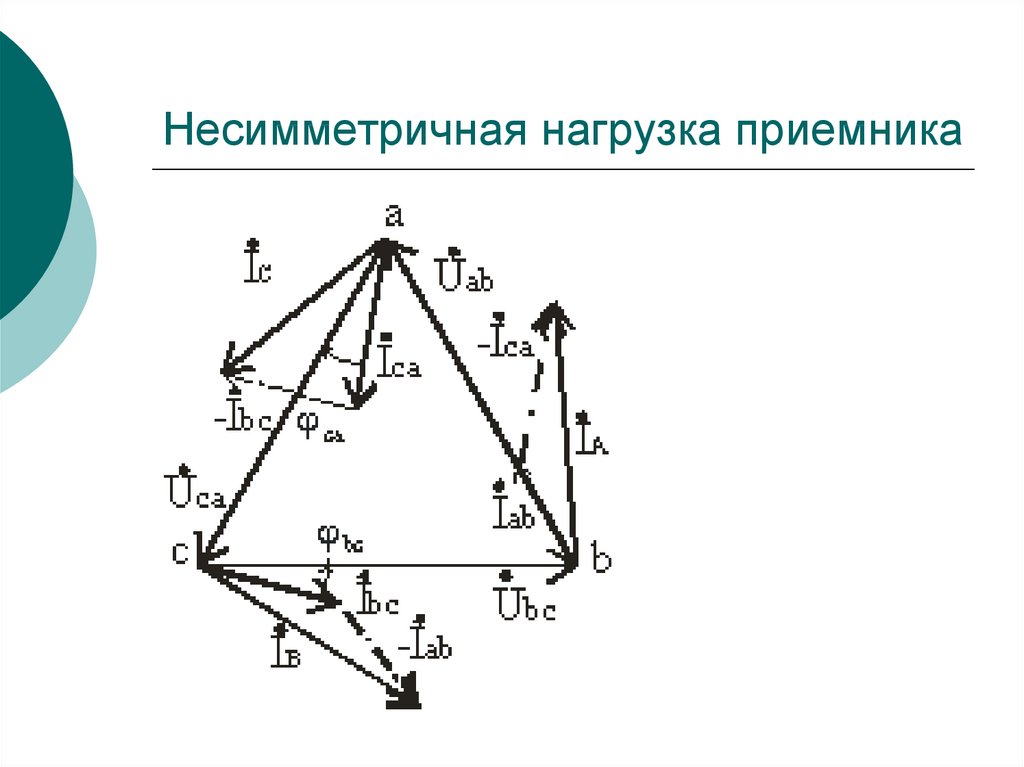
152. Несимметричная нагрузка приемника
153.
Таким образом, при несимметричной нагрузкесимметрия фазных токов İab, İbс, İca нарушается,
поэтому линейные токи İA, İB, İC можно определить
расчетом по вышеприведенным уравнениям или найти
графическим путем из векторных диаграмм.
Важной особенностью соединения фаз приемника
треугольником является то, что при изменении
сопротивления одной из фаз режим работы других
фаз остается неизменным, так как линейные
напряжения генератора являются постоянными. Будет
изменяться только ток данной фазы и линейные токи
в проводах линии, соединенных с этой фазой. Поэтому
схема
соединения
треугольником
широко
используется
для
включения
несимметричной
нагрузки.
При расчете для несимметричной нагрузки
сначала определяют значения фазных токов İab, İbc,
İca и соответствующие им сдвиги фаз φab, φbc, φca.
Затем определяют линейные токи в комплексной
форме или с помощью векторных диаграмм .
154. Общие замечания к расчету трехфазных цепей
1. При расчете трехфазных цепей исходят изпредположения,
что
генератор
дает
симметричную систему напряжений. На
практике несимметрия нагрузки практически
не
влияет
на
систему
напряжений
генератора в том случае, если мощность
нагрузки мала по сравнению с мощностью
генератора или сети электроснабжения.
2. Схема соединения обмоток трехфазного
генератора
не
предопределяет
схему
соединения нагрузки. Так, при соединении
фаз генератора в звезду нагрузка может
быть соединена в звезду с нейтральным
проводом, в звезду без нейтрального
провода или, наконец, в треугольник.
155. Мощность трехфазной цепи, ее расчет и измерение
В трехфазных цепях, так же как и в однофазных,пользуются понятиями активной, реактивной и
полной мощностей.
Соединение потребителей звездой
В общем случае несимметричной нагрузки
активная мощность трехфазного приемника
равна сумме активных мощностей отдельных
фаз
P = Pa + Pb + Pc,
где Pa = Ua Ia cos φa
Pb = Ub Ib cos φb;
Pc = Uc Ic cos φc
Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и
токи;
φa, φb, φc – углы сдвига фаз между
напряжением и током.
156.
Реактивнаямощность
соответственно
равна алгебраической сумме реактивных
мощностей отдельных фаз
Q = Qa + Qb + Qc,
где Qa = Ua Ia sin φa;
Qb = Ub Ib sin φb;
Qc = Uc Ic sin φc.
Полная мощность отдельных фаз
Sa = Ua Ia; Sb = Ub Ib; Sc = Uc Ic.
157.
Активная мощность симметричноготрехфазного приемника
P = 3 PФ = 3 UФ IФ cos φ.
Аналогично выражается и реактивная
мощность
Q = 3 QФ = 3 UФ IФ sin φ.
Полная мощность
S = 3 SФ = 3 UФ IФ.
Отсюда следует, что в трехфазной цепи при
симметричной системе напряжений и
симметричной
нагрузке
достаточно
измерить мощность одной фазы и утроить
результат.
158. Соединение потребителей треугольником
В общем случае несимметричной нагрузкиактивная мощность трехфазного приемника
равна сумме активных мощностей отдельных
фаз
P = Pab + Pbc + Pca,
где Pab = Uab Iab cos φab;
Pbc = Ubc Ibc cos φbc;
Pca = Uca Ica cos φca;
Uab, Ubc, Uca; Iab, Ibc, Ica – фазные
напряжения и токи;
φab, φbc, φca – углы сдвига фаз между
фазными напряжением и током.
159.
Реактивная мощность соответственно равнаалгебраической сумме реактивных
мощностей отдельных фаз
Q = Qab + Qbc + Qca,
где Qab = Uab Iab sin φab;
Qbc = Ubc Ibc sin φbc;
Qca = Uca Ica sin φca.
Полная мощность отдельных фаз
Sab = Uab Iab;
Sbc = Ubc Ibc;
Sca = Uca Ica.
Полная мощность трехфазного приемника
160.
Активная мощность симметричноготрехфазного приемника
P = 3 PФ = 3 UФ IФ cos φ.
Аналогично выражается и реактивная
мощность
Q = 3 QФ = 3 UФ IФ cos φ.
Полная мощность
S = 3 SФ = 3 UФ IФ.
161.
Или через линейные параметрыПри соединении фаз симметричного приемника
звездой UФ = UЛ /√3 , IФ = IЛ, при
соединении треугольником UФ = UЛ,
IФ = IЛ /√3
. Поэтому независимо от схемы
соединения
фаз
приемника
активная
мощность
при
симметричной
нагрузке
определяется одной и той же формулой
P = √3 UЛ IЛ cos φ.
Реактивная мощность
Q = √3 UЛ IЛ sin φ.
Полная мощность
S = √3 UЛ IЛ
162. Измерение активной мощности в трехфазных цепях
Измерение активной мощности втрехфазных
цепях
производят
с
помощью
трех,
двух
или
одного
ваттметров,
используя
различные
схемы их включения. Схема включения
ваттметров для измерения активной
мощности определяется схемой сети
(трех- или четырехпроводная), схемой
соединения фаз приемника (звезда или
треугольник),
характером
нагрузки
(симметричная или несимметричная),
доступностью нейтральной точки.
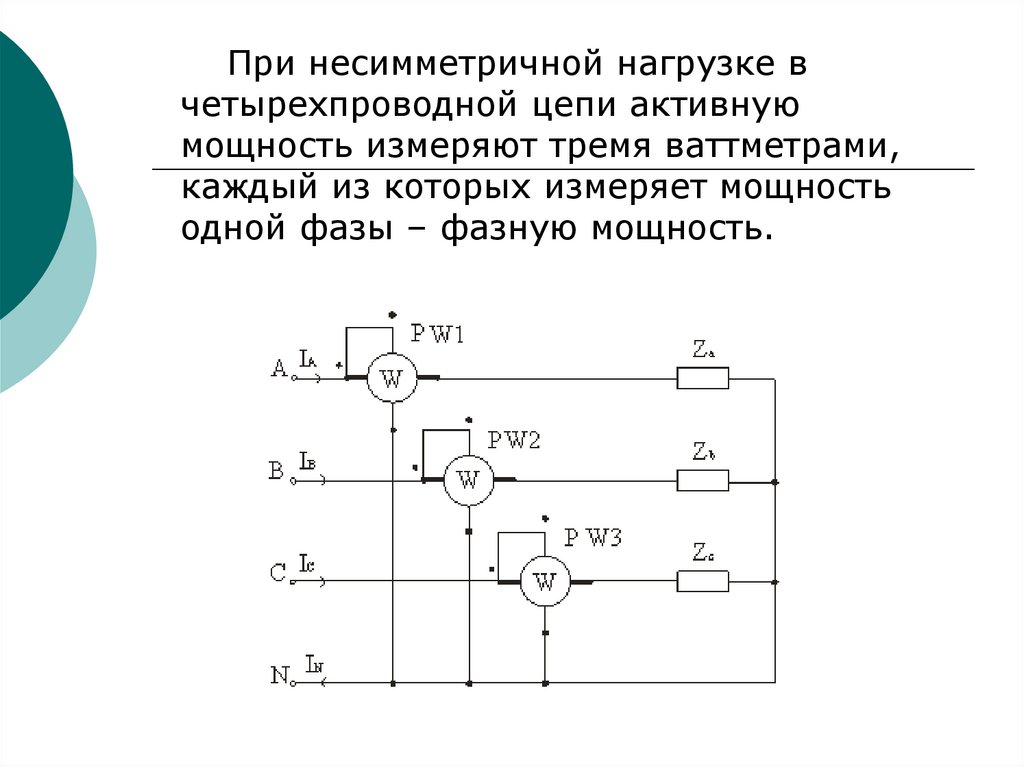
163.
При несимметричной нагрузке вчетырехпроводной цепи активную
мощность измеряют тремя ваттметрами,
каждый из которых измеряет мощность
одной фазы – фазную мощность.
164.
Активную мощность приемникаопределяют по сумме показаний трех
ваттметров
P = PА + P В + P С,
где PА = UA IA cos φA;
PВ = UB IB cos φB;
PС = UC IC cos φC.
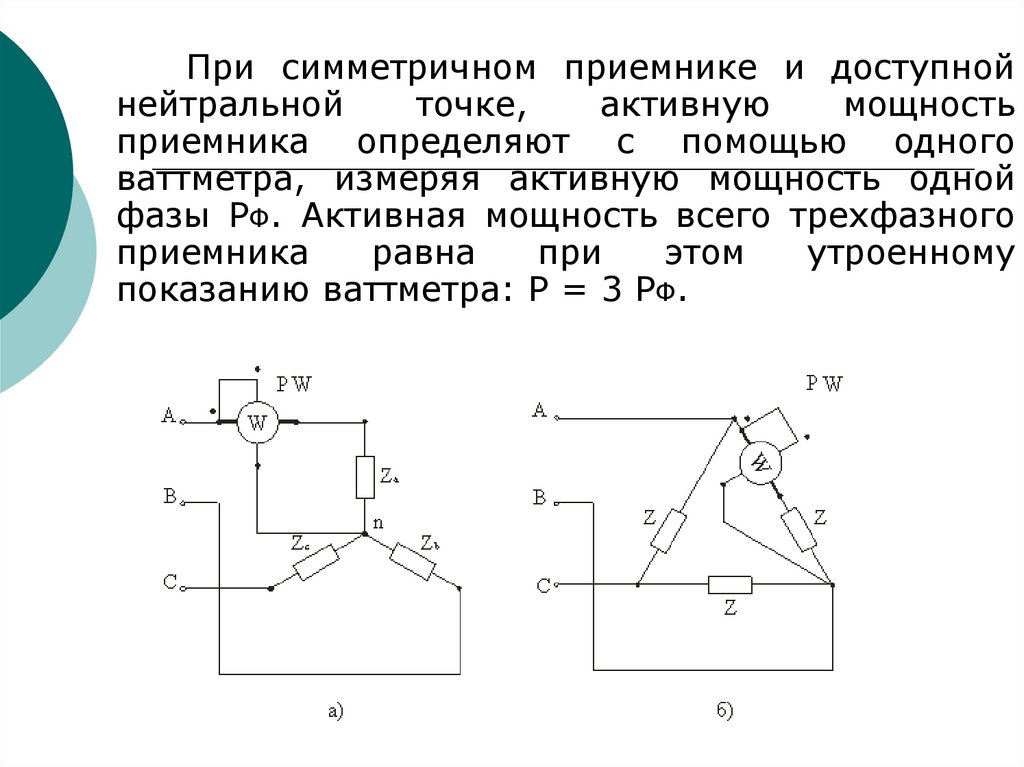
165.
При симметричном приемнике и доступнойнейтральной
точке,
активную
мощность
приемника определяют с помощью одного
ваттметра, измеряя активную мощность одной
фазы PФ. Активная мощность всего трехфазного
приемника
равна
при
этом
утроенному
показанию ваттметра: P = 3 PФ.
166. Измерение активной мощности двумя ваттметрами
В трехпроводных трехфазных цепяхпри симметричной и несимметричной
нагрузках и любом способе соединения
приемников
широко
распространена
схема измерения активной мощности
приемника
двумя
ваттметрами.
Показания
двух
ваттметров
при
определенной
схеме
их
включения
позволяют
определить
активную
мощность
трехфазного
приемника,
включенного в цепь с симметричным
напряжением источника питания.
167.
На схеме токовые катушки включены влинейные провода с токами IA и IB, а катушки
напряжения – соответственно на линейные
напряжения UAC и UBC.
P = UCA IA cos(UCA^IA) + UBC IB cos(UBC^IB) =
P1 + P2.



























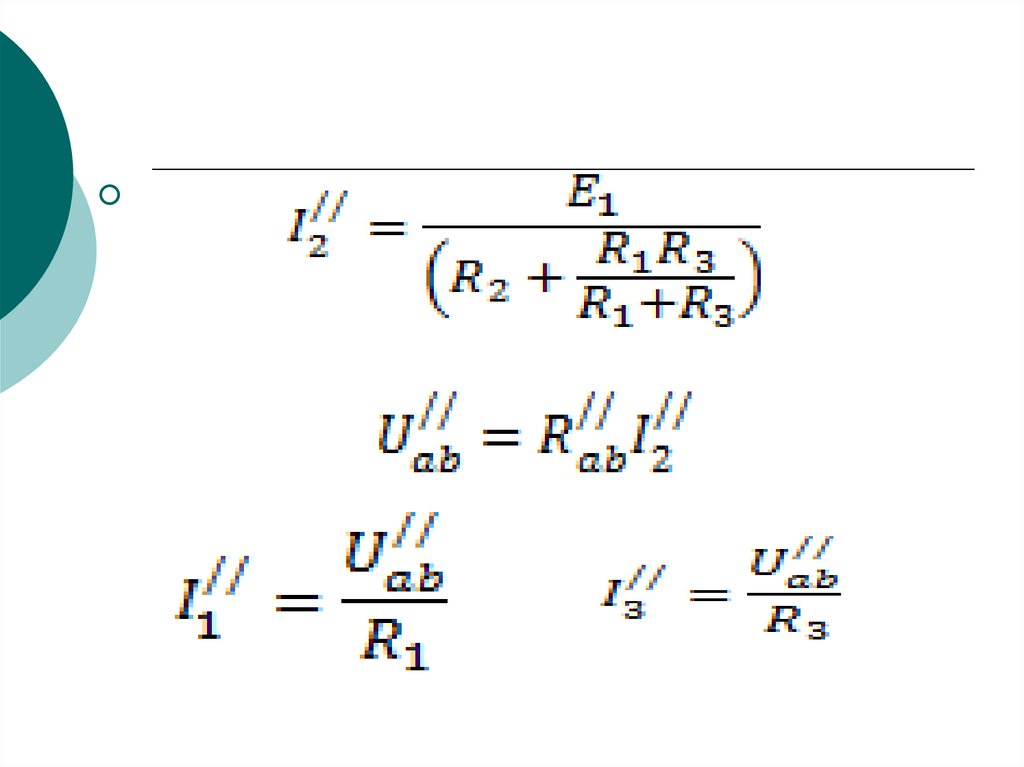
































































































 physics
physics








