Similar presentations:
Электростатика. Электр өрісінің потенциалы
1. ЭЛЕКТР ЖӘНЕ МАГНЕТИЗМ, АТОМДЫҚ ФИЗИКАНЫҢ АРНАЙЫ ТАРАУЛАРЫ
2. Электростатика
Электромагнетизмнің барлық құбылыстары және оның ерекшеліктері Максвеллтеңдеулері арқылы түсіндіріледі. Максвелл теңдеулері мыналар:
Е
,
0
Е
Электр өрісінің көзі – заряд.
В
,
t
Электр өрісінің құйыны айнымалы магнит
өрісі
Магнит өрісінің құйыны айнымалы
E
B 0
j 0 , электр өрісі және өткізгіш арқылы
t
өтетін ток
B 0.
Мұнда 0 1 / 0c 2
- магниттік тұрақты.
Магнит өрісінің көзі болмайтындығы,
яғни магнит өрісінің сызықтары
тұйықталған болатындығы
3. Электростатика
Е, j const
,
0
Е
В
,
t
Магнитостатика
B 0 j ,
B 0.
Егер зарядтар қозғалыссыз не ток
тұрақты болса, электр құбылысы
мен магнит құбылысы бір-біріне
тәуелсіз өмір сүреді, бір-біріне әсер
етпейді. Олардың өзара байланысы
зарядтар мен токтың шамалары
уақыт бойынша өзгере бастасымен
пайда болады.
4. Электр өрісінің потенциалы
Егер заряд тұйық контур бойымен тасылса, онда өрістің істейтін толықжұмысы нөлге тең болады W (a) W (b) 0
12
21
W12 (a) W21 (b)
2
E
W (1 2) Edl
2
1
2
2
Edl grad dl d (2) (1)
1
1
r
(r ) Edr
1
1
r
q
1 q
dr
2
4 0 r
4 0 r
(r )
j
1
qj
4 0 rj
5. Потенциалдық өріс. Элект өрісінің потенциалы.
1. Егер А векторлар өрісінің кез келген тұйық контур бойымен алынған циркуляциясынөлге тең болса, ол өріс потенциалдық болады.
2. Электростатикалық өрістің бірлік оң зарядты кез келген тұйық контур бойымен
айналдырып тасығанда істейтін жұмысы нөлге тең болса, онда ол электростатикалық
өрісті потенциалдық дейді.
3. Электростатикалық өрістің кез келген екі нүктесінің арасында бірлік оң зарядты
тасығандда өріс тарапынан істейтін жұмысы жолдың пішініне, ұзындығына
байланысты болмайды., тек бастапқы және соңғы нүктелердегі өріс сипаттамаларымен
анықталады.
4. Өрістің кез келген нүктесінің потенциалы – бірлік оң зарядты шексіздіктен қарастырып
отырған нүктеге әкелуге қажет болатын сыртқы күштің жұмысы.
5. Өрістің екі нүктесінің потенциал айырымы - бірлік оң зарядты сол нүктелердің
арасында тасығанда сырткы күштердің істейтің жұмысы.
6. Электростатикалық өрістің әр нүктесіне Е кернеулік векторымен қатар потенциалдыскалярды сәйкес қоюға болады. Потенциалдар электростатикалық өрісті энергия
жағынан сипаттамайды.
6. Өрістің потенциалы мен кернеулігі аралығындағы байланыс.
Өрістің потенциалы мен кернеулігі арасындағы байланысКейбір жағдайларда өріс кернеулігін анықтаудан гөрі өріс потенциалын анықтау жеңіл.
Сондықтан алдымен өріс потенциалын тауып, содан соң өріс кернеулігін есептеген
жөн.
7. Электростатиканың негізгі теңдеулері.
Электростатиканың негізгі теідеулері Максвелл теңдеулері:Е
,
0
Е 0,
,
0
,
0
2
2 2 2
,
х 2 y 2 z 2
2
Пуассон теңдеуі дейді.
Егер өріс көзі болып табылатын зарядтардың кеңістікке таралып орналасуы белгілі болса,
Пуассон теңдеуін шешу арқылы өрістің потенциалын тауып, содан соң өрістің кернеулігін
табамыз.
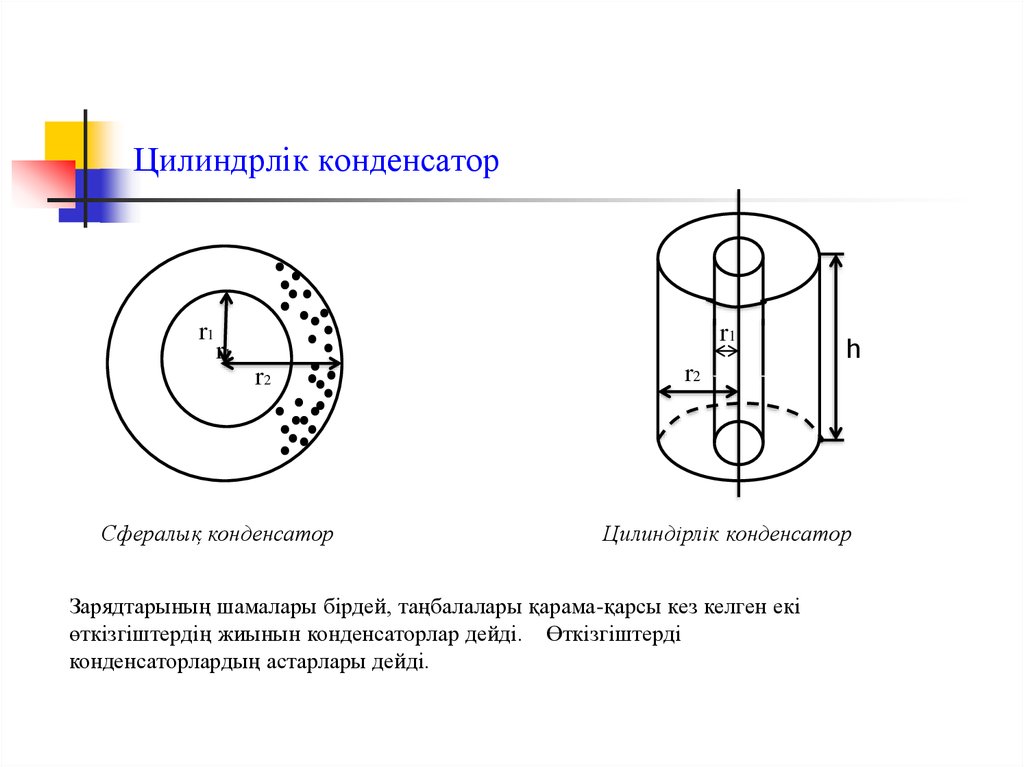
8. Сфералық, цилиндрлік және жазық конденсаторлар
Конденсаторлар бірінің ішінде бірі орналасқан өткізгіштерден жасалуы мүмкін:-сфералық конденсатор;
-цилиндрлік конденсатор;
-жазық конденсатор.
Конденсаторлардың сыйымдылықтарын анықтау үшін олардың астарларында
шоғырланған зарядтарды белгілідеп есептеп, потенциалдар айырымын
табамыз. Заряд шамасы мен потенциалдар айырымының пропоционалдық
коэффициенті сыйымдылықты береді.
а) Конденсатор сфералық болсын. Оның астарларындағы өрістің кернеулігі
E
q
4 0 r
2
мұнда q - конденсатор астарларындағы заряд.
Конденсатор астарларының арасындағы потенциал айырымы
r2
2 1 Edr
r1
1 1
4 0 r1 r2
q
Сфералық конденсатордың сыйымдылығы
C 4 0
r1r2
r2 r1
9. Цилиндрлік конденсатор
Конденсатор цилиндр тәріздес болсын. Конденсатордың ішкі астарларындағызаряд q болсын. Гаусс теоремасы бойынша кернеулік ағыны
2 hE
E
q
0
1
q
4 0 r h
қатынасымен анықталады
Жазық конденсаторды
а) Конденсатор сфералық болсын. Оның астарларындағы өрістің кернеулігі
E
q
4 0 r
2
мұнда
- конденсатор астарларындағы заряд.
q
Конденсатор астарларының арасындағы потенциал айырымы
r2
2 1 Edr
r1
1 1
4 0 r1 r2
q
Сфералық конденсатордың сыйымдылығы
C 4 0
r1r2
r2 r1
10. Цилиндрлік конденсатор
r1r1
r1
r2
Сфералық конденсатор
h
r2
Цилиндірлік конденсатор
Зарядтарының шамалары бірдей, таңбалалары қарама-қарсы кез келген екі
өткізгіштердің жиынын конденсаторлар дейді. Өткізгіштерді
конденсаторлардың астарлары дейді.
11. Цилиндрлік конденсатор
Астарларының арасындағы потенциалдар айырымын ескеріпr2
2 1 Edr
r1
q
4 0h
ln
r2
r1
Кейінгі теңдіктен цилиндрлік кондерсатордың сыйымдылығы үшін
C 2 0h / ln
r2
r1
Жазық конденсатор. Оның астарындағы заряд шамасы q болсын. Конденсатор
астарларының арасындағы потенциал айырымы электростатикалық өрістің
кернеулігі Е арқылы анықталады.
Ed
E
q
0 S
Жазық конденсатор сыйымдылығы
C
0S
d
d
q
0S
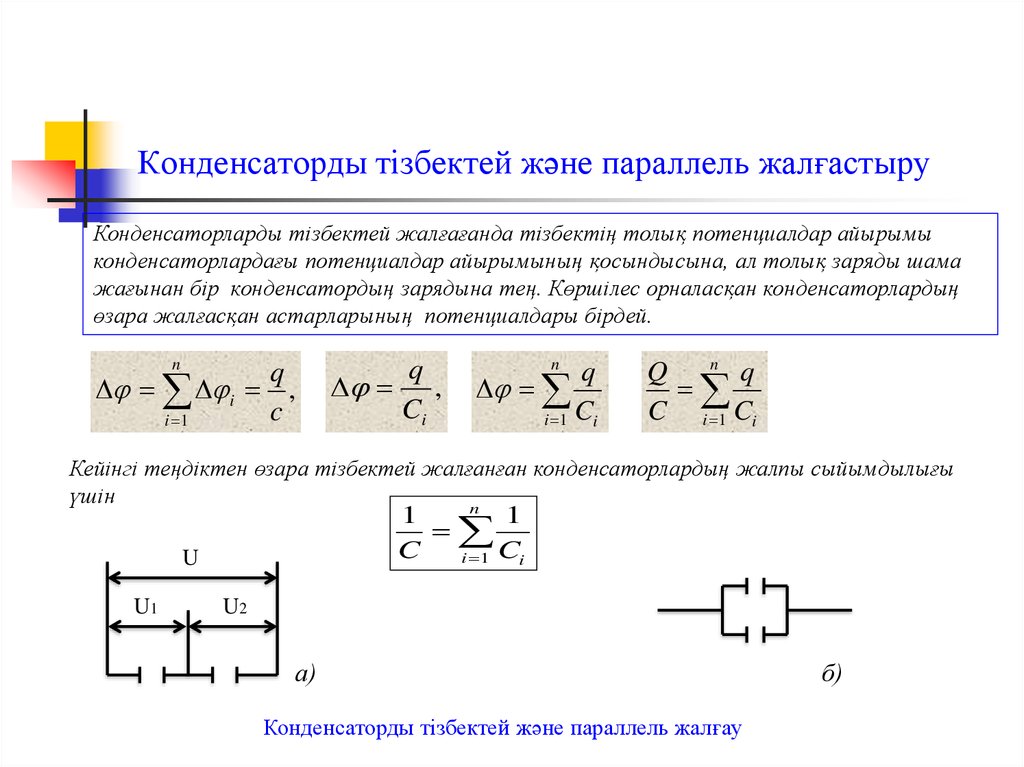
12. Конденсаторды тізбектей және параллель жалғастыру
Конденсаторларды тізбектей жалғағанда тізбектің толық потенциалдар айырымыконденсаторлардағы потенциалдар айырымының қосындысына, ал толық заряды шама
жағынан бір конденсатордың зарядына тең. Көршілес орналасқан конденсаторлардың
өзара жалғасқан астарларының потенциалдары бірдей.
n
q
i ,
c
i 1
q
,
Ci
n
q
i 1 Ci
n
Q
q
C i 1 Ci
Кейінгі теңдіктен өзара тізбектей жалғанған конденсаторлардың жалпы сыйымдылығы
үшін
n
1
1
C
i 1 Ci
U
U1
U2
а)
Конденсаторды тізбектей және параллель жалғау
б)
13. Конденсаторды тізбектей және параллель жалғастыру
2 Параллель жалғанған конденсаторлардың астарларындағы потенциал айырымыбірдей , ал зарядтары әр түрлі. Конденсаторларда шоғырланған зарядтар
q1 C1 ,
q2 C 2 ,
..........
qn C n
Конденсатордың толық заряды:
n
q qi (C1 C2 ... Cn )
i 1
Екінші жағынан
q C
Кейінгі екі теңдіктен параллель жалғанған конденсаторлардың толық сыйымдылығы:
n
C Ci
i 1
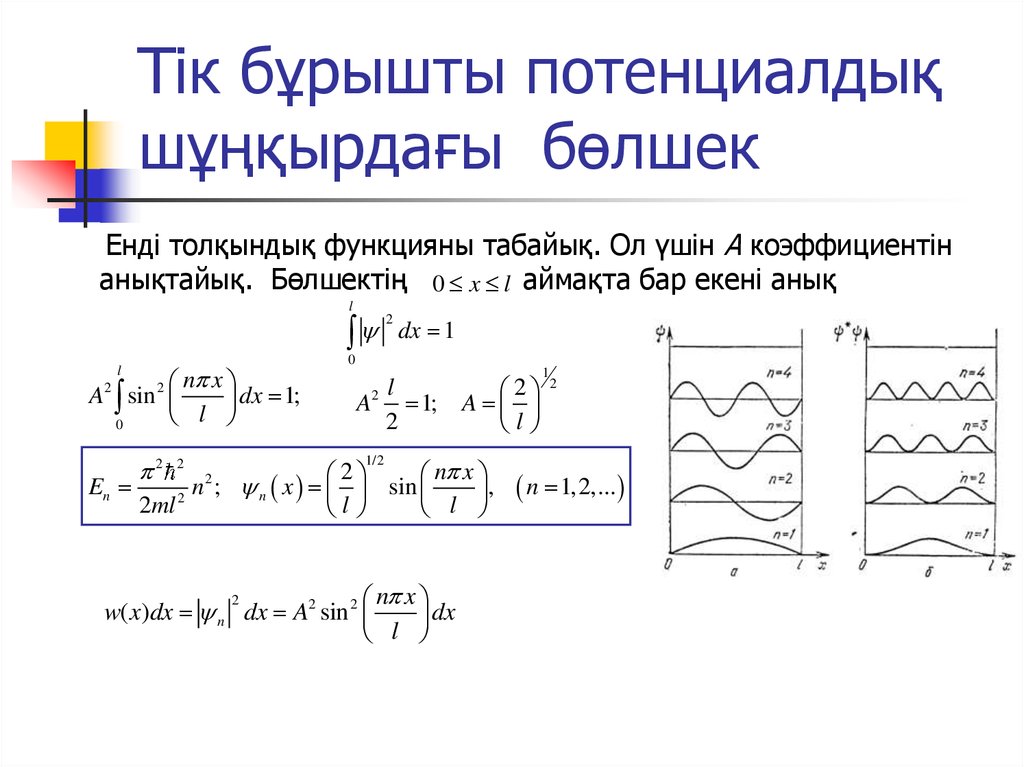
14. Тік бұрышты потенциалдық шұңқырдағы бөлшек
0 x болғанда U=0x<0 және x> болғанда U= болады
d 2 2m
2 ( E U ) 0
dx 2
Үздіксіздік шартынан
k2
2m
2
(0) (l ) 0
d 2 2m
2 E 0
dx 2
E
(0) 0; B 0;
(l ) 0;
'' k 2 0
( x) Asin kx B cos kx
( x) Asin kx
(l ) A sin kl 0;
En
kl n n 1,2,...
2
2
2ml
2
n 2 n 1, 2,...
k2 2
E
2m
15. Тік бұрышты потенциалдық шұңқырдағы бөлшек
Енді толқындық функцияны табайық. Ол үшін А коэффициентінанықтайық. Бөлшектің 0 x l аймақта бар екені анық
l
dx 1
2
n x
A sin
dx 1;
l
0
l
2
2
2
0
l
A2 1;
2
2
A
l
2
n x
En
n
;
x
sin
n
,
2
2ml
l
l
1/2
2
2
2
n x
w( x)dx n dx A2 sin 2
dx
l
1
2
n 1, 2,...
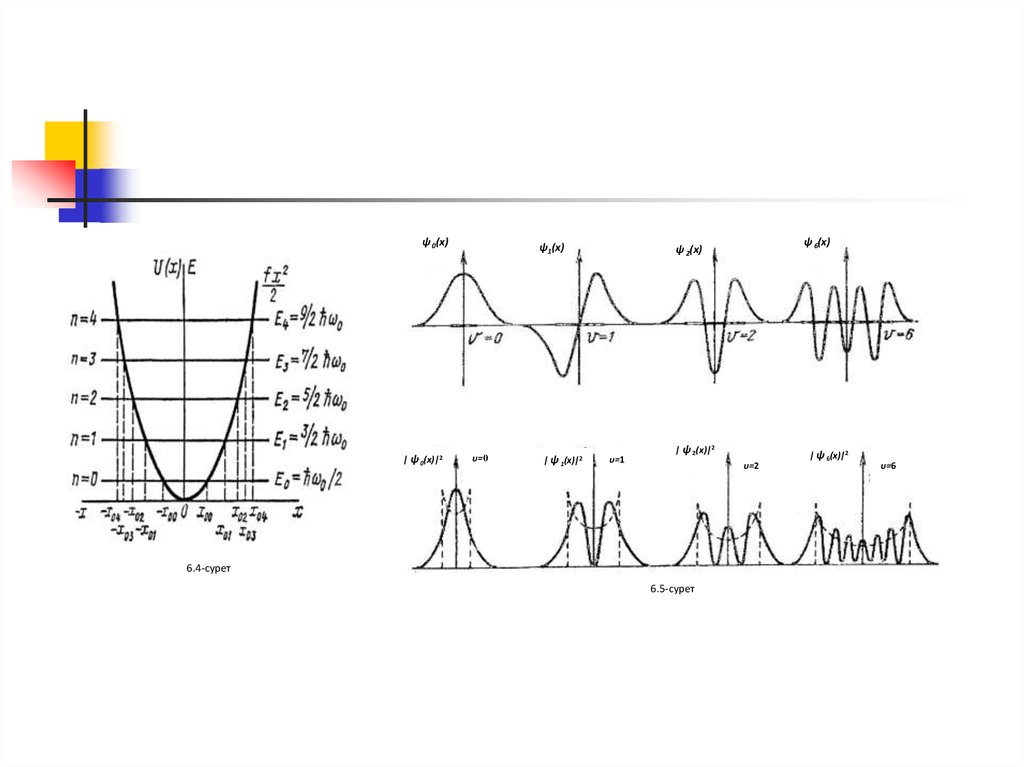
16. Сызықтық гармоникалық осциллятор
Массасы m бөлшек х осі бойында бөлшектің тепе-теңдік қалыптан ауытқуына турапропорционал F=-kx квазисерпімді күш әсерінен қозғалатын болсын. Мұндағы k –
серпімділік коэффициенті. Осындай бөлшек сызықтық гармоникалық осциллятор деп
аталады.
Гармоникалық осциллятордың ротенциалдық энергиясы
kx 2
U ( x)
2
k
0
m
m 02 x 2
U ( x)
2
Осциллятор үшін Шредингер теңдеуі
d 2 2m
m 02 x 2
0
2 E
2
2
dx
мұндағы Е – осцилятордың толық энергиясы. Е параметрі мына мәндерді
E ( 12 ) 0( 0,1,2,...)
17.
ψ 0(х)| ψ 0(х)|2
ψ1(х)
υ=0
| ψ 1(х)|2
ψ 6(х)
ψ 2(х)
υ=1
| ψ 2(х)|2
υ=2
6.4-сурет
6.5-сурет
| ψ 6(х)|2
υ=6
18. Орталық-симметриялы өрісте бөлшектің қозғалысы. Сутегі атомының квантмеханикалық моделі
Шредингер теңдеуі. Енді сутегі ядросының кулондық өрісіндеэлектронның күйі жайындағы квант-механикалық есепті
шығаруға көшейік. Заряды Ze ядроны координаттар
жүйесінің басы деп қабылдаймыз. Сонда потенциалдық
энергия сфералық симметриялық тартылыс өрісі (кулондық)
түрінде болады:
2
Ze
U( r )
4 0 r
Гамильтонның классикалық функциясы былайша жазылады:
2
1
Ze
H
( Px2 Py2 Pz2 )
2m0
4 0 r
мұндағы m0 – электрон массасы, Px, Py, Pz – импульс
құраушылары.
19.
Осы алынған өрнекті Гамильтонның операторына түрлендіреміз:2
ˆ
H
U (r )
2m0
Осы операторды электронның толқындық функциясына
қолданғанда сутегі атомы үшін Шредингер теңдеуін аламыз:
2
Ze 2
2m 4 r E
0
0
x r sin cos
y r sin sin
z r cos
(7.1)
мұндағы – Лаплас операторы,
Е – электронның толық энергиясы.
2 2 2 1 2
2 2 2 2 r
x y z
r r r
1
2
r
7.1-сурет
1
1 2
1
(sin
)
r 2 ,
2
2
sin
r
sin
(7.2)
20.
(7.2) өрнекті (7.1) теңдігіне қойғаннан кейін Шредингер теңдеуімына түрде жазылады:
(7.3)
мұндағы
1
2
r 2 , K 0
r
2
2
m
Ze
2
K 20 E
4 0 r
(7.3) теңдеудегі К тек r координатына тәуелді; r тек радиал
функцияға, ал - сфералық функцияға әсер ететін
операторлар. (7.3) теңдеуді айнымалыларды айыру әдісімен
шешеміз. Ол үшін -функцияны екі функция көбейтіндісі түрінде
іздестіреміз
( r , , ) R( r ) Y ( , ),
мұндағы R(r) толқындық функцияның радиалдық бөлігі немесе
радиалдық функция деп аталады. Y( , ) функциясы және
бұрыштық координаттарға тәуелді. Бұл сфералық, кейде
шарлық функция деп аталады.
21. Радиалдық толқындық функциялар теңдеуі
Енді толқындық функцияның R(r) радиалдық бөлігі үшін теңдеугекөшейік. Бұл теңдеуді мына түрде жазуға болады:
2m0
1 d 2 d
Ze 2 l( l 1 )
r
R 2 E
R 0
2
2
4 0 r
r dr dr
r
(7.5)
мұнда r және мәндері ескерілген.
E<0 болғанда (7.5) теңдеуінің -функцияға қойылатын табиғи
талаптарды (бірмәнділік, шектелген, үздіксіздік) қанағаттандыратын
шешімдері Е-нің дискретті мәндері жағдайында, яғни мынаған тең
m0e4 Z 2 1
болғанда алынады:
E En
2
(7.6)
2 2 2
32 0
n
Сутегі атомындағы электрон энергиясы квантталған, яғни бас
кванттық санмен анықталатын дискреттік мәндер қабылдайды.
(7.6)-дағы n=n + +1 нөлден үлкен, бүтін сан (n=1, 2, 3,..., ).
n саны - бас кванттық сан, ал n =nr=(n- -1) – радиал кванттық сан
деп аталады.
Еn үшін дәл Бор теориясындағыдай өрнек алынғандығы; бірақ мұның
кванттық механиканың қатаң заңдары негізінде қорытылып
шығарылғандығы.
22.
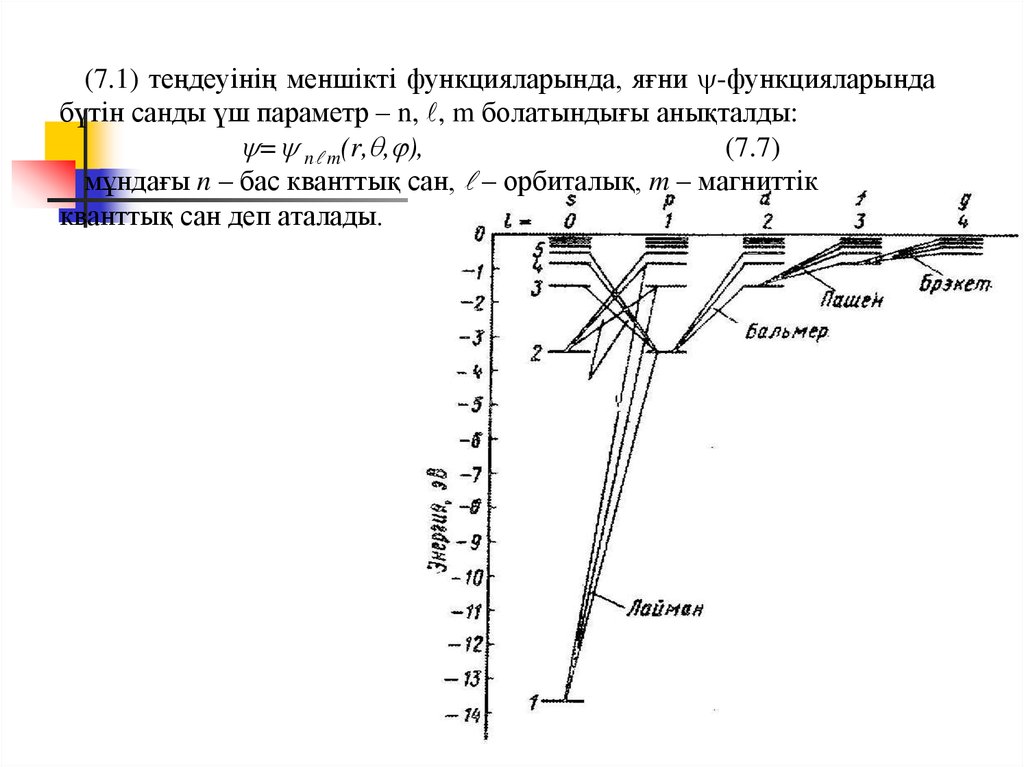
(7.1) теңдеуінің меншікті функцияларында, яғни -функцияларындабүтін санды үш параметр – n, , m болатындығы анықталды:
= n m(r, , ),
(7.7)
мұндағы n – бас кванттық сан, – орбиталық, m – магниттік
кванттық сан деп аталады.
23. Сутегі атомындағы электронның энергия деңгейлері. Энергия деңгейлерінің айнуы.
(7.6) өрнектегі z=1 болғанда сутегі атомының энергетикалықдеңгейлері үшін өрнек алынады
m0e4
.
Ry
1
En
2 2 ,n 1,2,...
2 2 2
32 0 n
n
1Ry=1,79 10-16 Дж 13,6 эВ.- атомның энергия шкаласының
(7.8)
масштабын анықтайды
(7.8) теңдеуіне m кванттық саны енбеген, демек электронның
энергия мәні бұған тәуелді емес. Сонда мәні тұрақты, ал m әр
түрлі болатын барлық күйлер (мұндай күйлердің толық саны
2 +1) бірдей энергияға ие болады. Демек бір энергия деңгейіне
әртүрлі -функциялармен бейнеленетін бірнеше күй сәйкес
келеді. Осындай энергетикалық деңгейлер айныған, ал нақты
энергия мәні бірдей күйлер саны сол энергия деңгейінің айну
дәрежесі деп аталады. n 1
2( n 1 ) 1 1
( 2l 1 )
n 1 3 5 ... 2n 1 n 2
2
l 0
24.
Атомдық физикада импульс моменттерінің мәндері әр түрліэлектрон күйлерінің спектроскопиядағы шартты белгіленуі
пайдала-нылады. Сонда =0 күйде тұрған электронды sэлектрон, =1 күйдегі электронды – p-электрон, =3 күйдегі
электронды – d-электрон деп атайды.
Электрон күйін көрсету үшін (әрине бір электронды сутегі атомы
жағдайында бұл атомның күйін де көрсетеді) мынадай
символдық жазу қолданылады: санының шартты белгісі
алдына n бас кванттық санның мәні жазылады. Мысалы, n=2
және =1 сандары бар электрон күйі 2р символымен белгіленеді.
-дің максимум мүмкін мәні n мәнінен 1-ге кем болатындықтан,
атомда электронның мынадай күйлері мүмкін болады
1s
2s, 2p,
3s, 3p, 3d және т.б.



















 physics
physics








