Электр зарядының сақталу заңы

1. № 9 лекция Электростатика

2. Жоспары

1.Электр зарядының сақталу заңы.
2.Кулон заңы.
3.Электр өрісі. Электр өрісінің кернеулілігі.
4.Кернеулік векторының ағыны.
5.Вакуумдағы электр өрісі үшін ОстроградскийГаусс теоремасы. .
6. Электр өрісінің күшінің жұмысы.
7. Циркуляция.
8.Потенциал.
8.Потенциалдық электр өрісінің кернеулігімен
байланысы.

3. Электр зарядының сақталу заңы

Зерттеу жұмыстарында (1910—1914) американдық физик Р.
Милликен (1868—1953) электр зарядының дискретті, яғни
кез келген дененің заряды q элементар электр зарядынан
тұратынын көрсетті.
q ne
е=1,6∙10-19 Кл
me=9,11∙10-31 кг

4.

Зерттеу жұмыстардың нәтижесінде фундаменталды табиғат
заңы ашылды, 1843ж. ағылшын физигі М. Фарадей тәжірибе
жүзінде электр зарядының сақталу заңын тұжырымдады:
Кез келген тұйық жүйеде барлық бөлшектер
зарядтарының алгебралық қосындысы өзгеріссіз
қалады .
q q1 q2 q3 ... qn const
Электр зарядының өлшем бірлігі — кулон (Кл) — бұл ток күші
1 А болғанда, өткізгіштің көлденең қимасынан 1 с уақытта
өтетін электр заряды.

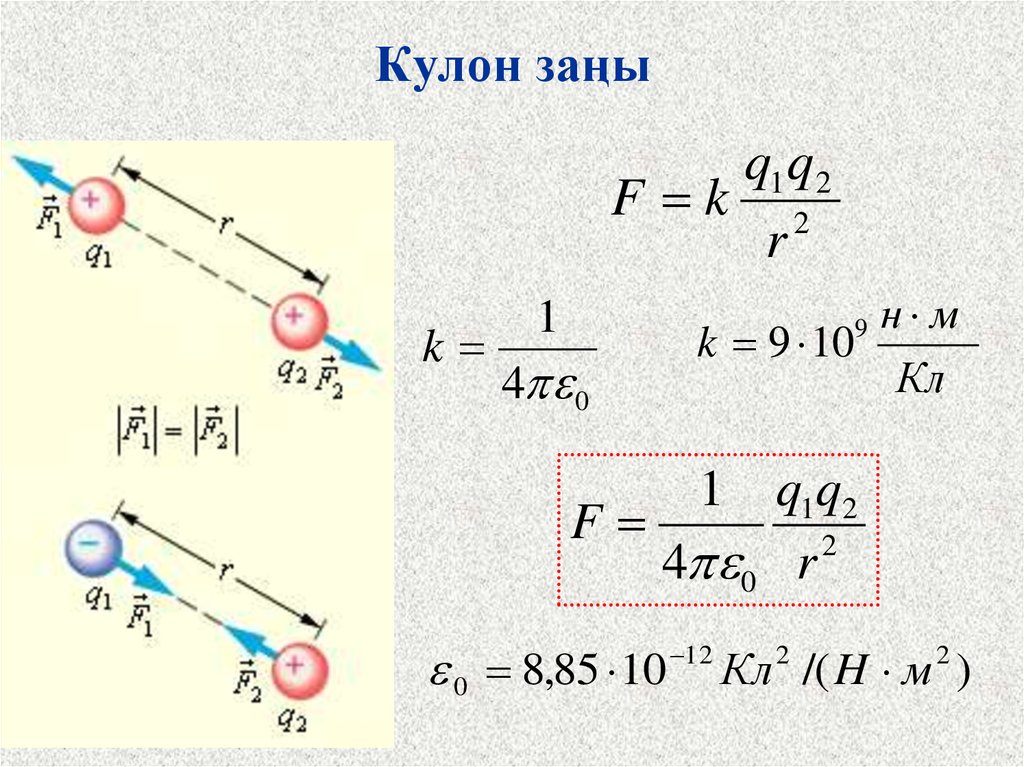
5. Кулон заңы

q1q2
F k 2
r
k
1
н м
k 9 10
Кл
9
4 0
q1q2
F
2
4 0 r
1
0 8,85 10
12
Кл /( H м )
2
2

6. Электростатикалық өріс. Электростатикалық өрістің кернеулігі.

Берілген нүктедегі
Электростатикалық өрістің
кернеулігі өрістің осы
нүктесінде орналасқан
бірлік оң зарядқа әсер
ететін күшпен
анықталатын физикалық
шама болып табылады.
E F / q0
Вакуумдағы нүктелік заряд
өрісінің кернеулігі
1
q
E
.
2
4 0 r
немесе
q
E k 2.
r
Е векторының бағыты сол өрістегі оң зарядқа әсер
ететін күштің бағытымен сәйкес келеді. Егер өріс
оң зарядтан турса, онда Е векторы радиусвектордың бойымен зарядтан сыртқы ортаға
бағытталады (оң зарядтан тебіледі); егер өріс теріс
зарядтан турса, онда Е векторы зарядқа қарай
бағытталады.

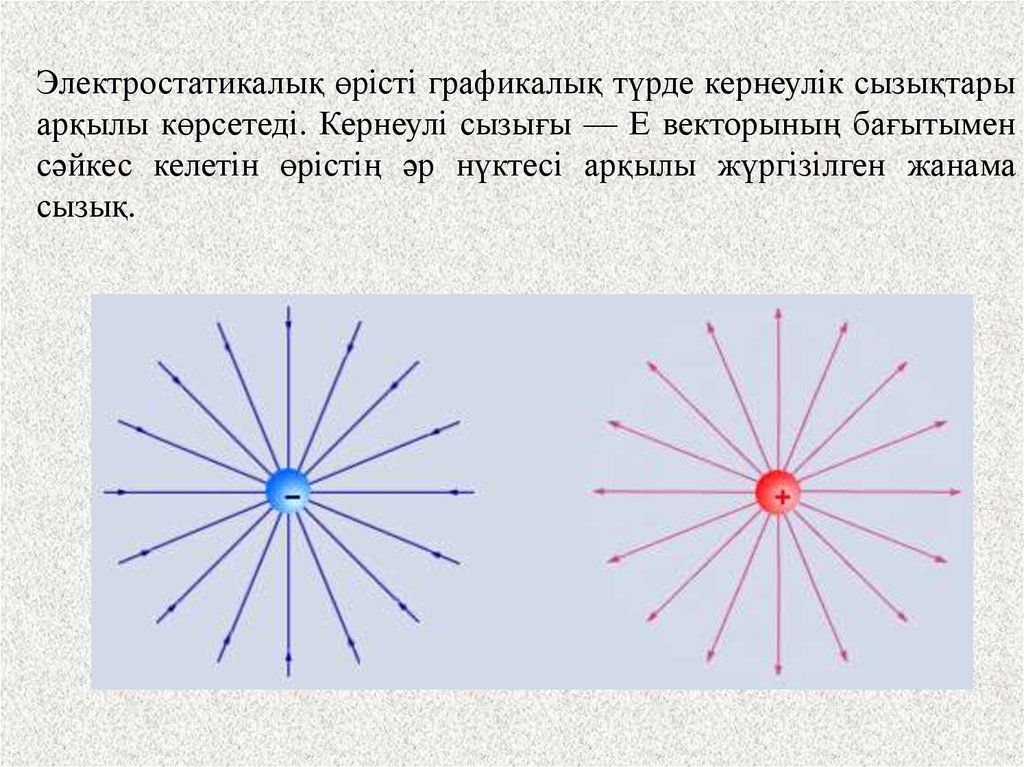
7.

Электростатикалық өрісті графикалық түрде кернеулік сызықтары
арқылы көрсетеді. Кернеулі сызығы — Е векторының бағытымен
сәйкес келетін өрістің әр нүктесі арқылы жүргізілген жанама
сызық.

8.

9.

Суперпозиция принципы

10.

Егер өріс бірлік зарядтан турса, онда кернеулік сызықтары —
түзу, егер оң заряд болса, зарядтан шығады, егер теріс заряд
болса,сол зарядқа кіреді.
n
E Ei
i 1
E E1 E2 ... En Ei

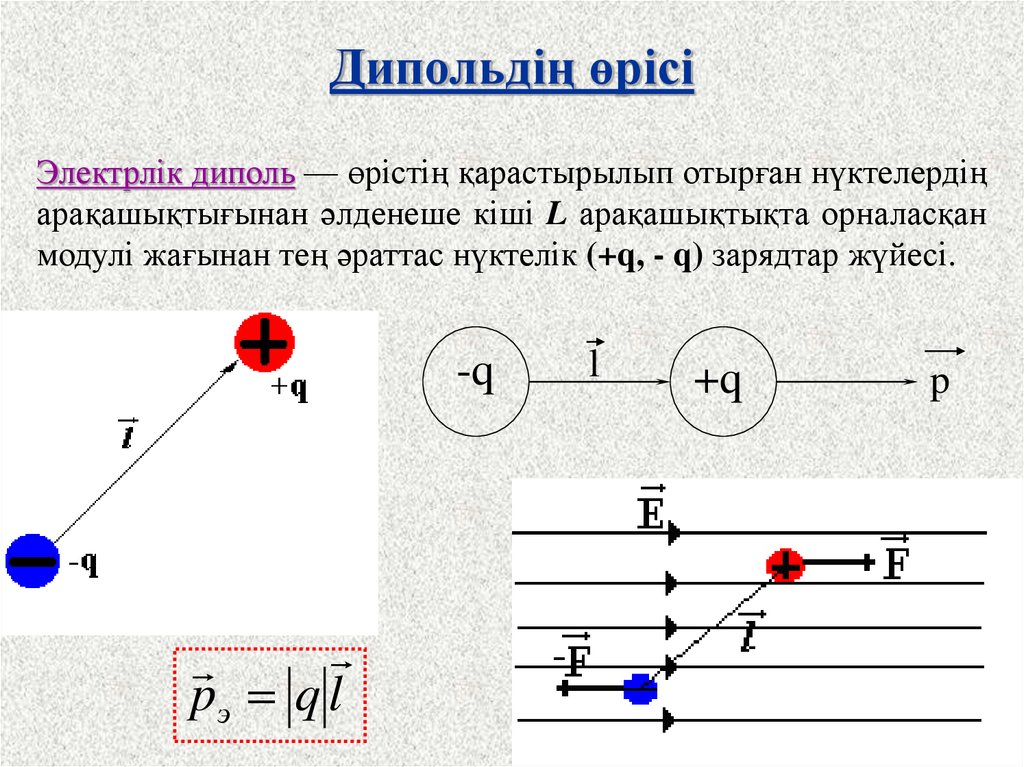
11.

Дипольдің өрісі
Электрлік диполь — өрістің қарастырылып отырған нүктелердің
арақашықтығынан әлденеше кіші L арақашықтықта орналасқан
модулі жағынан тең әраттас нүктелік (+q, - q) зарядтар жүйесі.
-q
pэ q l
l
+q
p

12.

Суретте суперпозиция принципінің қолданылуы мысалы
ретінде l арақашықтықта орналасқан модулі жағынан бірдей,
заряды q және –q жүйе –электрлік диполь өрісінің күш
сызықтары көрсетілген.
Электрлік диполь өрісінің
күш сызықтары

13.

Кернеулік векторының ағыны
dФЕ EdS cos Еn dS
ФЕ Еn dS EdS ,
s
s
dS dSn

14.

Кернеулік векторының ағыны
Е векторының ағыны кез келген тұйық S жазықтықты
қиып өтеді.

15.

Кернеулік векторының ағыны
1
q
E
2
4 0 R
ФЕ Еn dS EdS ,
s
1
s
q
q
2
Ф En dS
4 R
2
4 0 R
0
s

16. Вакуумдағы электростатикалық өріс үшін Гаусс теоремасы

К. Гаусс теоремасы кез келген тұйық жазықтық арқылы өтетін злектр өрісінің
кернеулік векторының ағынын анықтайды.
Тұйық және нүктелік q зарядтан тұратын кез
келген формадағы жазықтық үшін Е векторы
q/ε0 тең болады, яғни
ФE EdS En dS q / 0
S
S
Ағынның таңбасы q зарядының таңбамен сәйкес
келеді.

17.

Гаусса теоремасын мына түрде жазуға болады:
n
1
EdS En dS q
S
0
S
1
EdS En dS
S
S
0
i 1
dV .
V

18. Кейбір вакуумдағы электростатикалық өрістерді есептеу үшін Гаусс теоремасын қолдану.

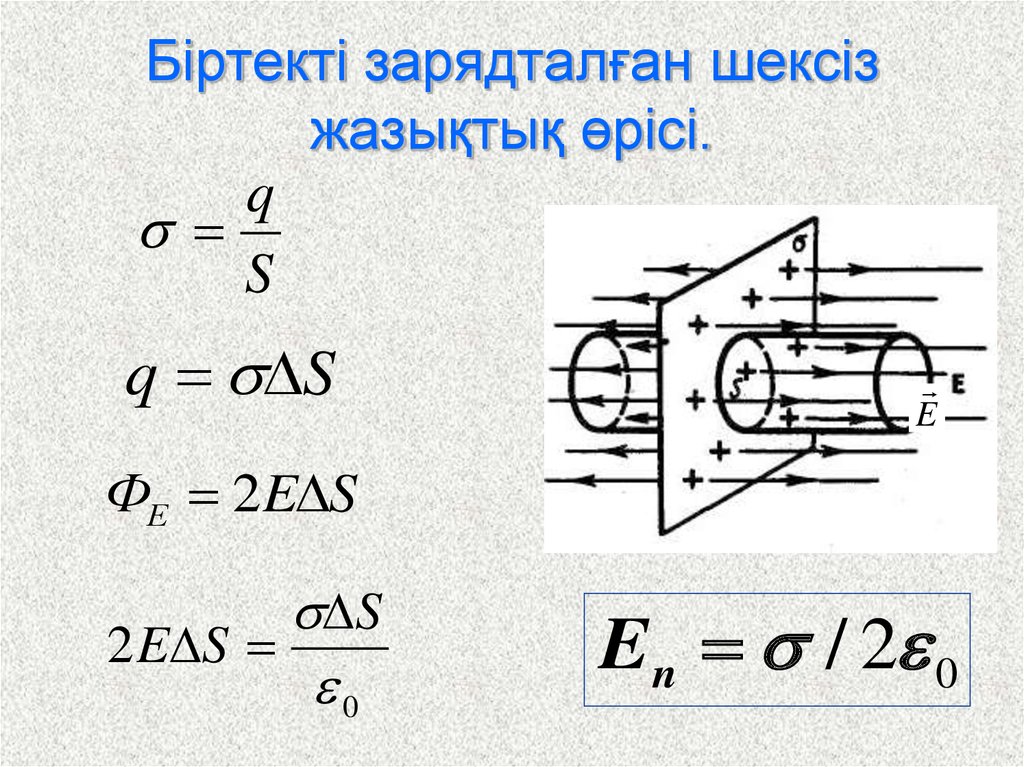
19. Біртекті зарядталған шексіз жазықтық өрісі.

q
S
q S
E
ФЕ 2E S
S
2 E S
0
En / 2 0

20. Екі шексіз өзара параллель зарядталған жазықтықтардың өрісі

E1 E 2
,
2 0
E A E1 E 2
EA E1 E2 0
EС E1 E2
EС E1 E2 0
E В E1 E 2
E В E1 E 2 2
2 0 0
EВ / 0

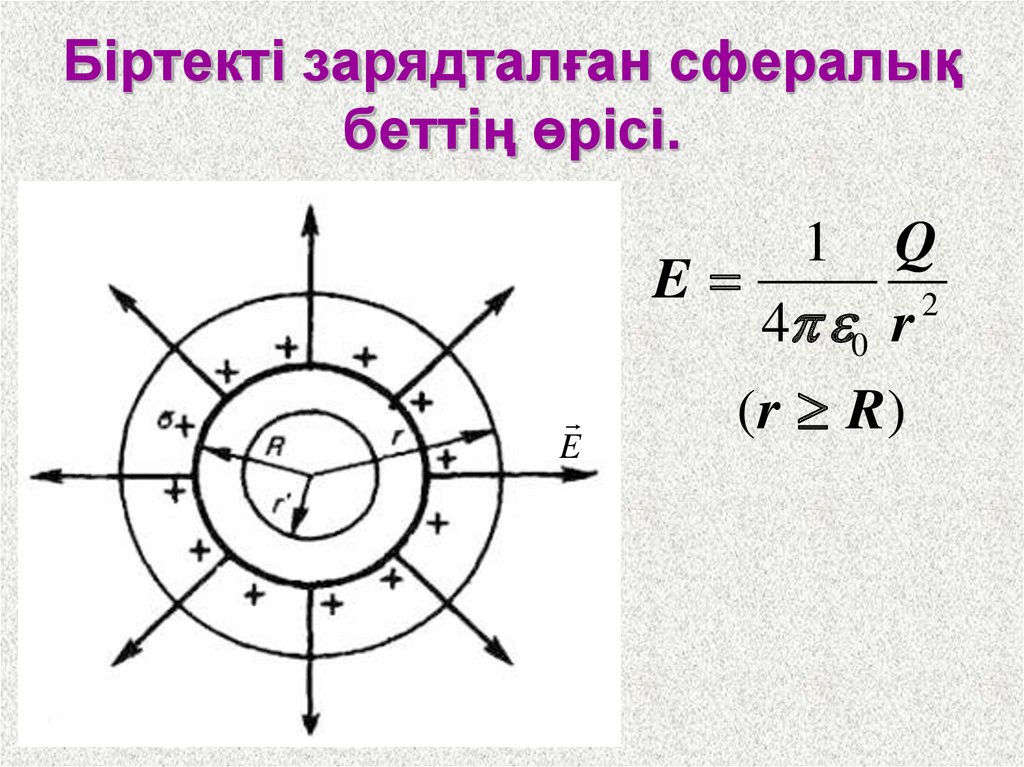
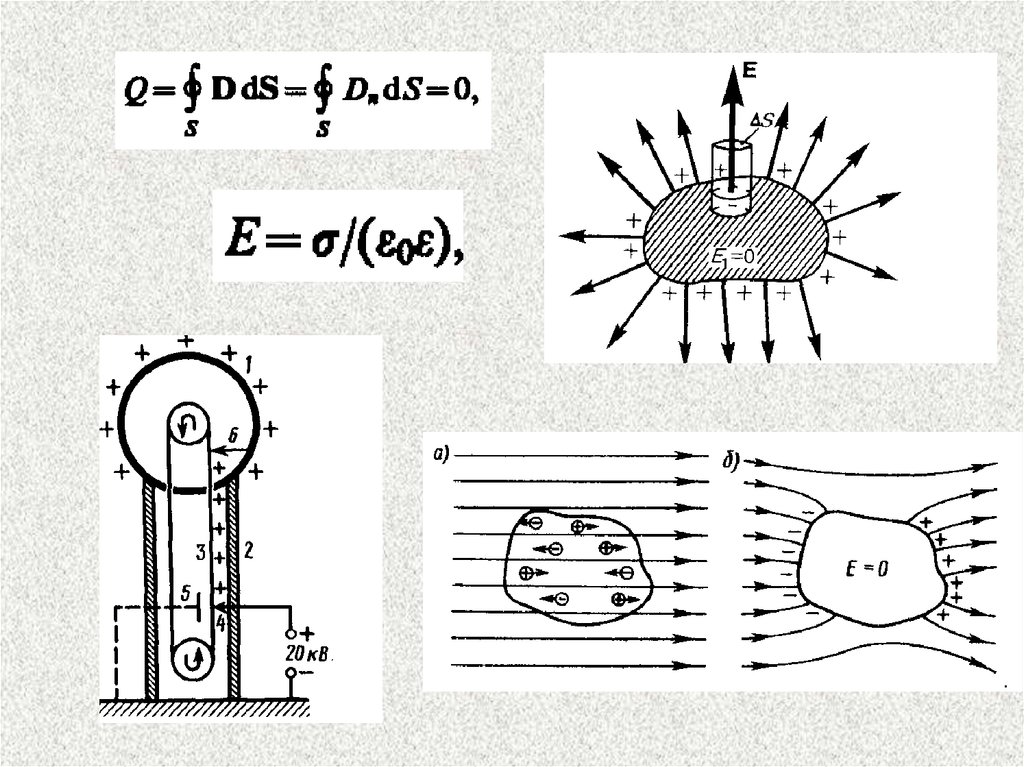
21. Біртекті зарядталған сфералық беттің өрісі.

1
Q
E
2
4 0 r
E
(r R)

22.

r>R кезінде өріс нүктелік
зарядтағы
заңдылық
бойынша г қашықтыққа
кемиді. Суретте r-ден
тәуелді Е-нің графигі
көрсетілген. Егер r'<R
болса,
онда
тұйық
жазықтық ішінде заряд
болмайды,
сондықтан
біртекті
зарядталған
сфералық беттің ішінде
электростатикалық
өріс
болмайды (Е=0).

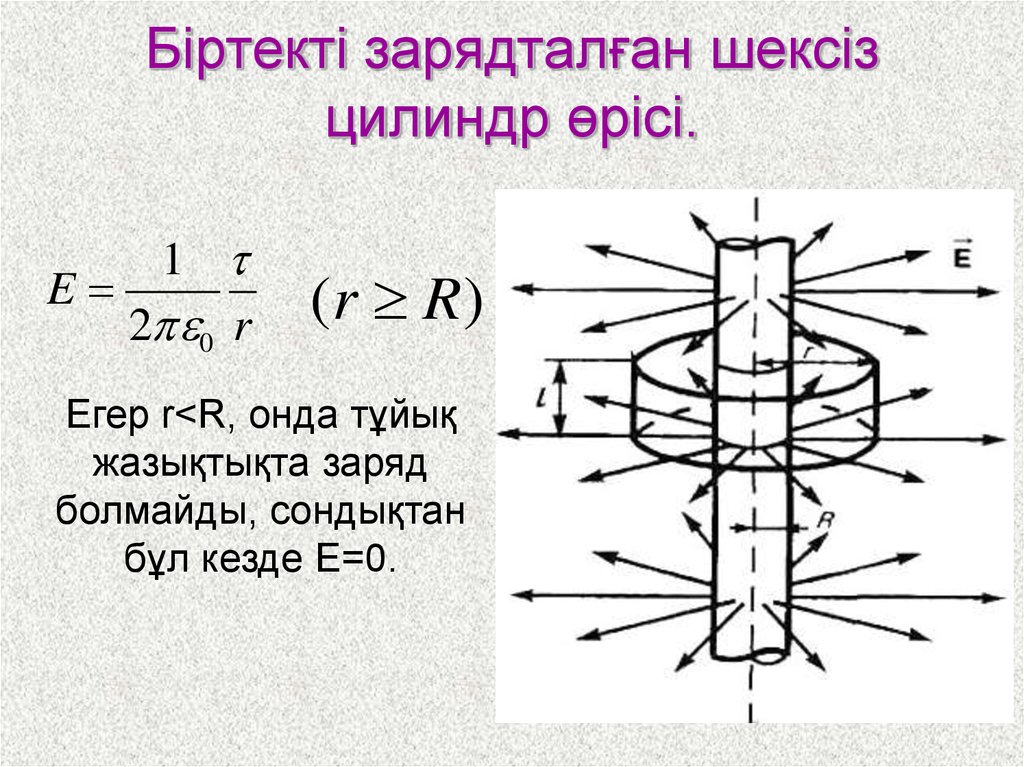
23. Біртекті зарядталған шексіз цилиндр өрісі.

1
E
2 0 r
(r R)
Егер r<R, онда тұйық
жазықтықта заряд
болмайды, сондықтан
бұл кезде E=0.

24.

Электростатикалық өріс потенциалдық болып
табылады.
Электростатикалық өріс күшінің жұмысын q
зарядының өрісінің бастапқы және соңғы
нүктелеріндегі q0 нүктелік зарядтың потенциалдық
энергиясының айырымы ретінде көрсетуге болады
:
qq0
1 qq0
A12
U1 U 2 .
4 0 r1
4 0 r2
1
1 нүктесінен 2 нүктесіне орын ауыстырған q0
зарядтың өріс күшінің жұмысы мына түрде де
жазыла алады:
A12=U1- U2=q0(φ1 - φ2).

25.

яғни бастапқы және соңғы нүктелердегі
потенциалдарының айырмасын орын ауыстырған
заряд шамасына көбейткенге тең. Электр өрісінің
1 және 2 нүктелерінің потенциалдарының
айырмасы бірлік оң зарядтың өріс күшінің
әсерінен 1 нүктесінен 2 нүктесіне орын
ауыстырғанда істелетін жұмыс шамасымен
анықталады.

26.

Сонымен қатар 1 нүктесіне 2 нүктесіне
электростатикалық өріс күшінің әсерінен
орын ауыстырған q0 зарядтың жұмысы
мына түрде беріле алады :
A12 q0 Ed

27. Бағытталған электростатикалық өрістің кернеулік векторының циркуляциясы:

Ц Е ( Е dl ) 0
l
F
1
Ц Е
dl
q
q
проб
.
проб.
l
l
1
1
F dl dA
q0 1 2
ql
qпроб.
1 2 Ц Е 0
l
dl
E

28. Электр өріс потенциалы

A
q0
U
q0
1
q
4 0 r

29.

A12 U 1 U 2 q0 1 2
A12 q0 Ed
2
1 2 Ed
q0 1 2 q0 Ed
U q
1
1 2 Ed
U Ed

30. Электр өрісінің кернеулігі мен φ потенциал арасындағы байланыс.

E grad
Декарттық координат жүйесінде:
E
i
j
y
z
x
Егер өріс біртекті және Х осі бойымен
бағытталса, онда:
E
i
x
k

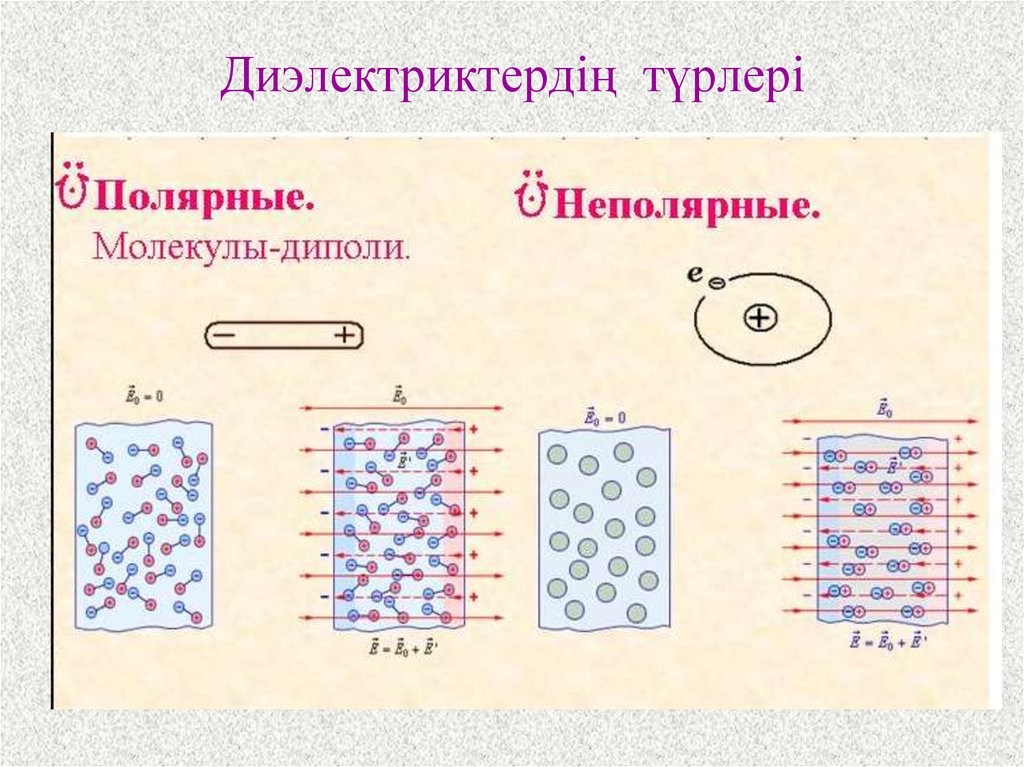
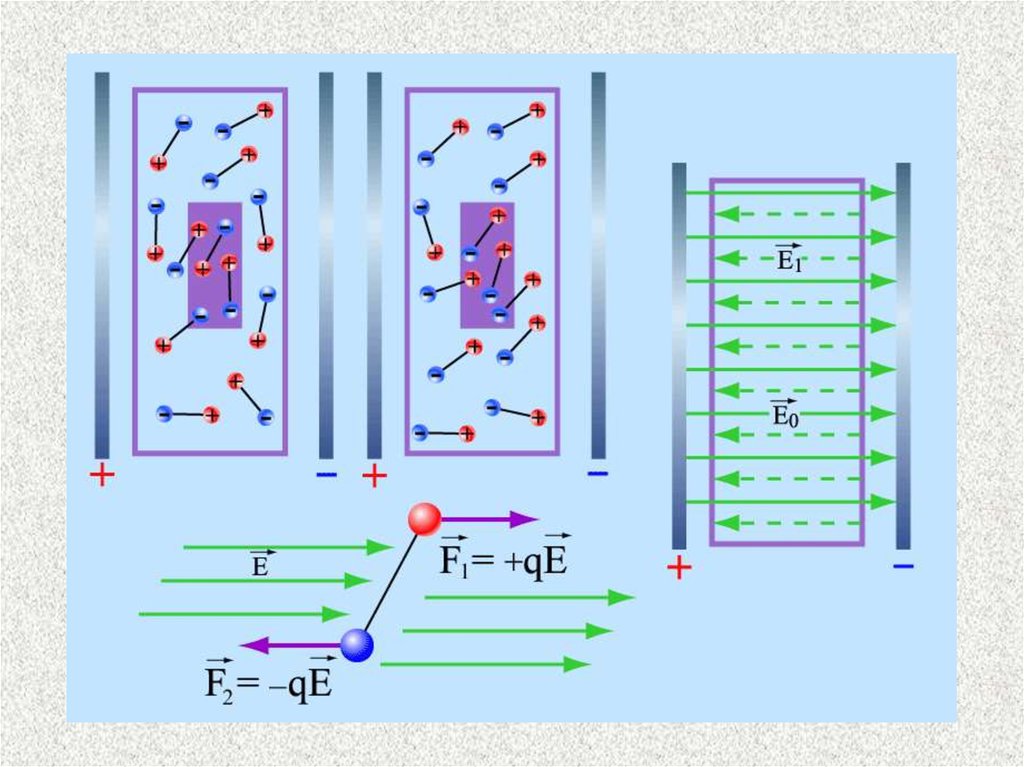
31. Диэлектриктердің түрлері

32.

33.

34.

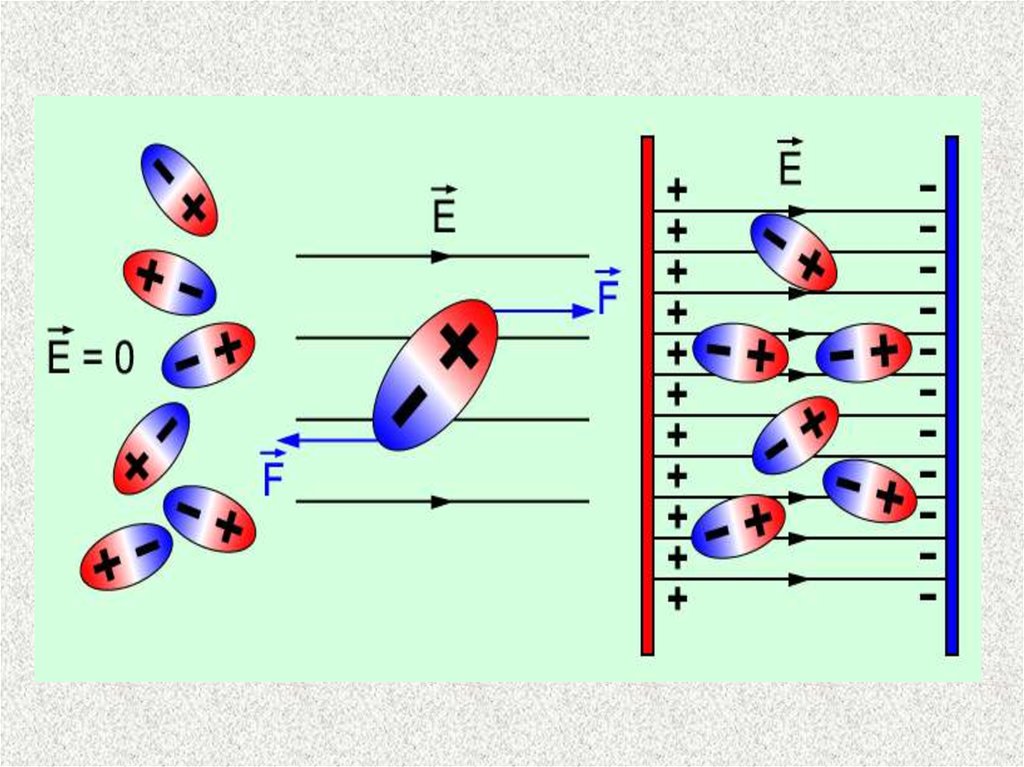
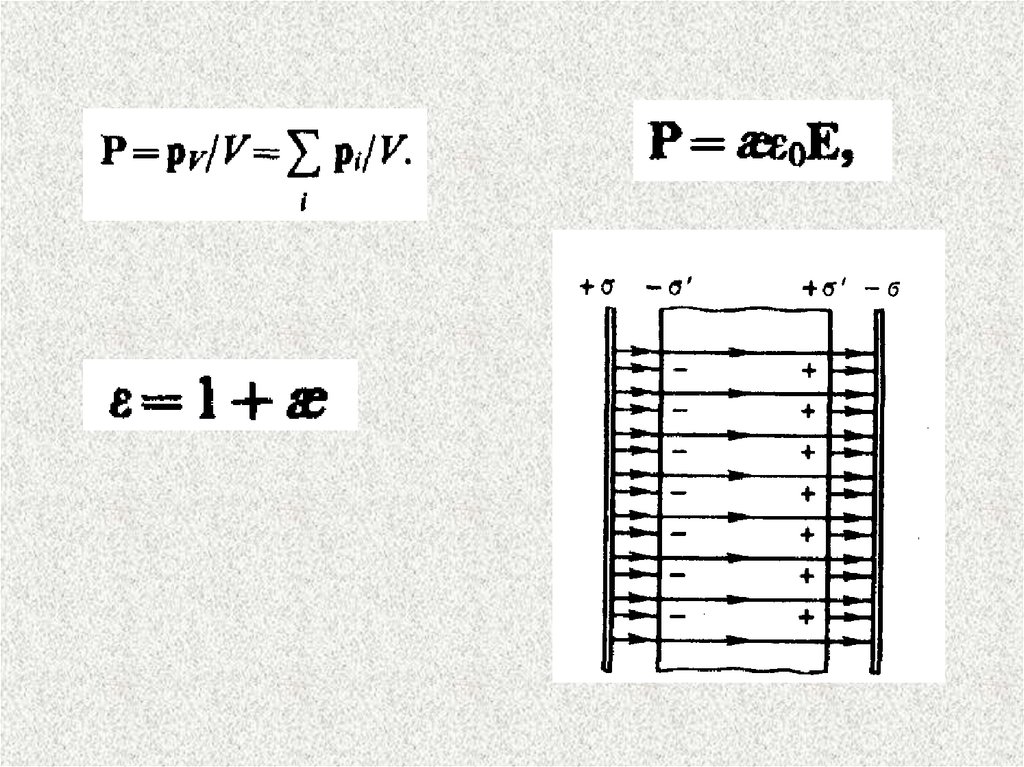
35. Электр ығысу векторы

Диэлектриктегі электростатикалық
өріс үшін Гаусс теоремасы

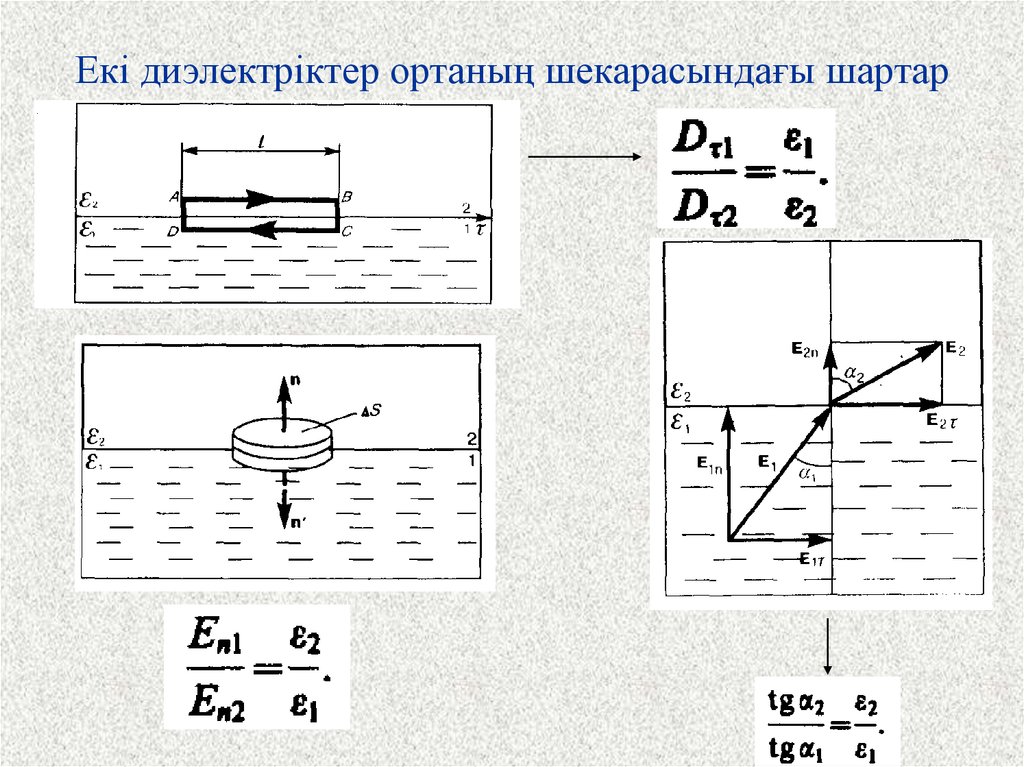
36. Екі диэлектріктер ортаның шекарасындағы шартар

37.

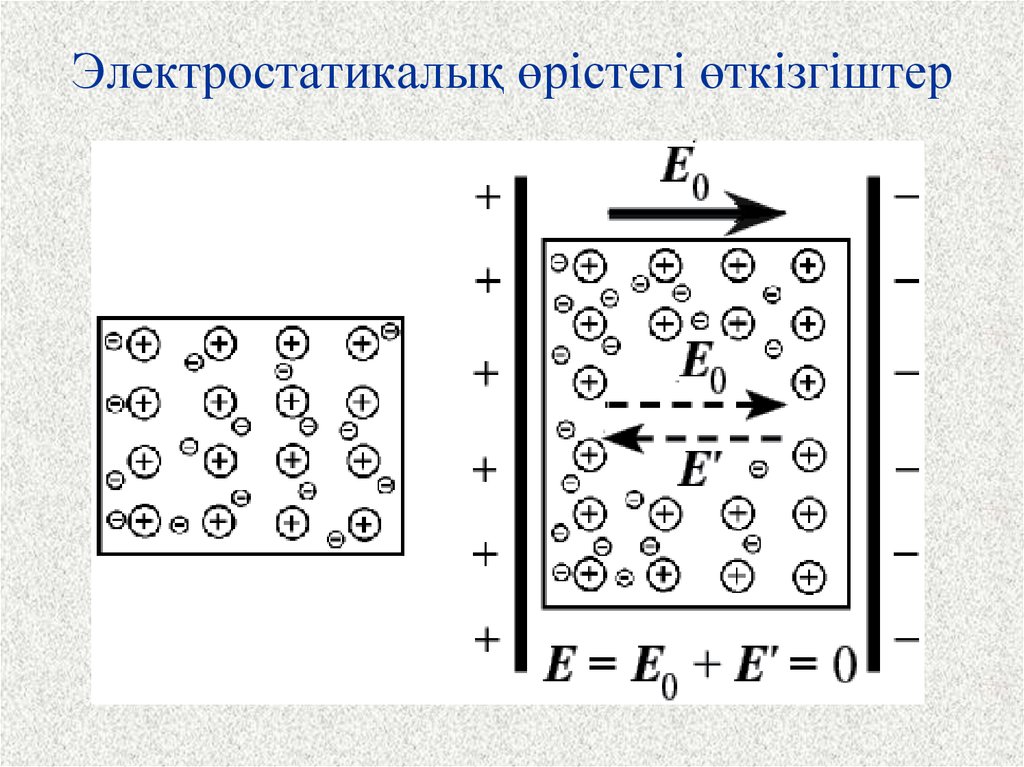
38. Электростатикалық өрістегі өткізгіштер

39.

40. Электросыйымдылық

41.

42.

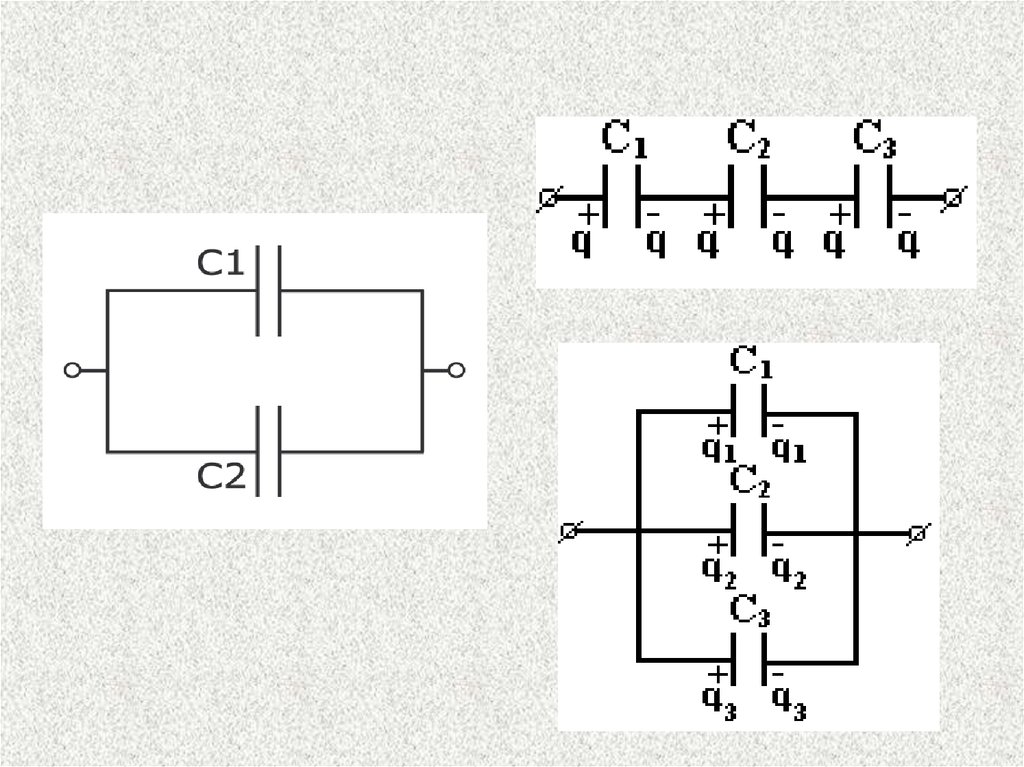
Конденсаторлар
жазық
Цилиндрлық
Сфералық
Параллель жалғау:
Тізбектеп жалғау:

43. Электростатикалық өріс энергиясы

q 2 q C 2
W
2C
2
2
2
q 2 qU CU 2
W
2C
2
2
2
q
q
W
x
2C 2 0 S
dW
q2
F
dx
2 0 S

44. ДӘРІСТІҢ СОҢЫ