Similar presentations:
Векторлар өрісі және оның сипаттамалары
1. ЭЛЕКТР ЖӘНЕ МАГНЕТИЗМ, АТОМДЫҚ ФИЗИКАНЫҢ АРНАЙЫ ТАРАУЛАРЫ
2. Векторлар өрісі және оның сипаттамалары.
Әр нүктесіне белгілі бір ғана вектор сәйкес қойылған кеңістікті векторлар өрісі дейді.Кез-келген нүктесінде жүргізілген жанамасының бағыты өрістің векторының бағытымен
дәл келетін сызықтарды векторлар өрісінің сызықтары дейді.
(Мысалы, E және B векторларының өрісі)
Өрістің сызықтары басталатын (аяқталатын) кеңістіктің нүктесінде оның көзі (құйылысы)
бар дейді.
Айналасында өрістің сызықтары
тұйықталып тұрған нысанды өрістің
E
құйыны дейді.
(Мысалы, айнымалы электр, айнымалы магнит өрістері және электр тогы болады)
Векторлар өрісі табиғаттары әртүрлі, көз және құйын деген физикалық нысандардың
әсерінен болады.
Кез-келген бетті перпендикуляр бағытта қиып өтетін өріс сызықтарының санын векторлар
өрісінің ағыны дейді.
Векторлар өрісіндегі кез-келген тұйық контур бойымен алынған вектордың интегралын
өрістің циркуляциясы дейді.
Кез-келген векторлар өріс өзінің көзімен және құйынымен толық анықталады.
Көлем шамасын нөлге ұмтылдырғанда, оны қоршап тұрған сыртқа бағытталған ағын, өріс
нүктесіндегі көзінің қуатын, ал беттің ауданын нөлге ұмтылдырсақ, ол керіп тұрған
тұйық контур бойынша алынған циркуляцияның, өріс нүктесіндегі құйынының қуатын
алады.
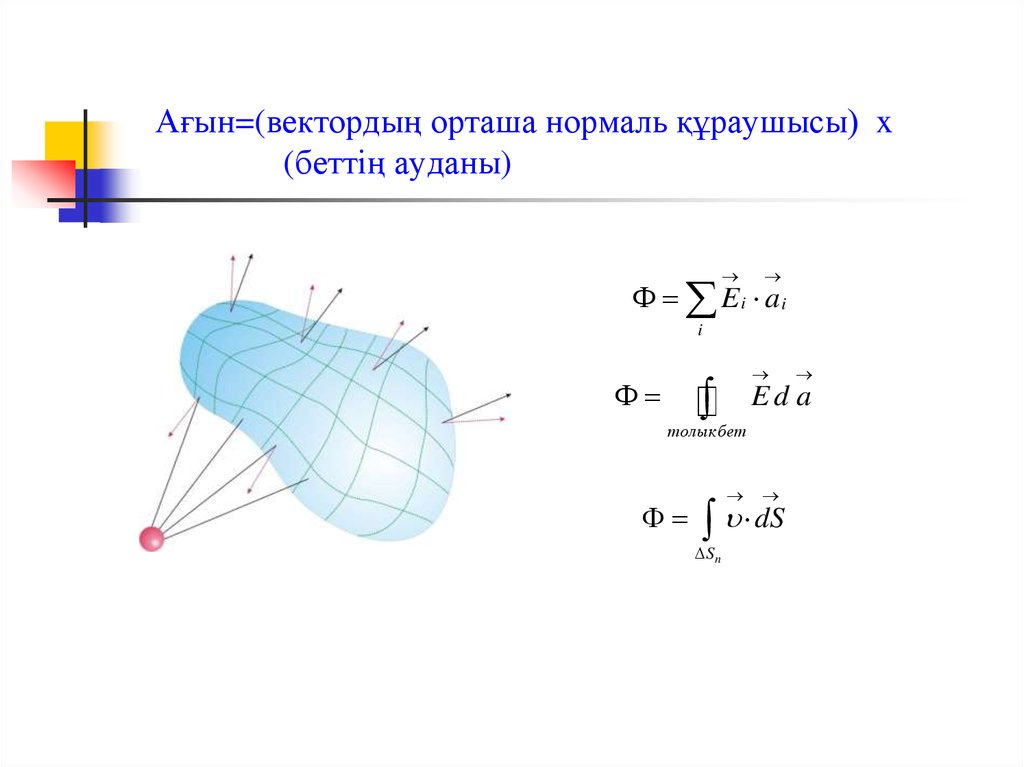
3. Ағын=(вектордың орташа нормаль құраушысы) x (беттің ауданы)
Ei aii
Ed a
толык бет
dS
S n
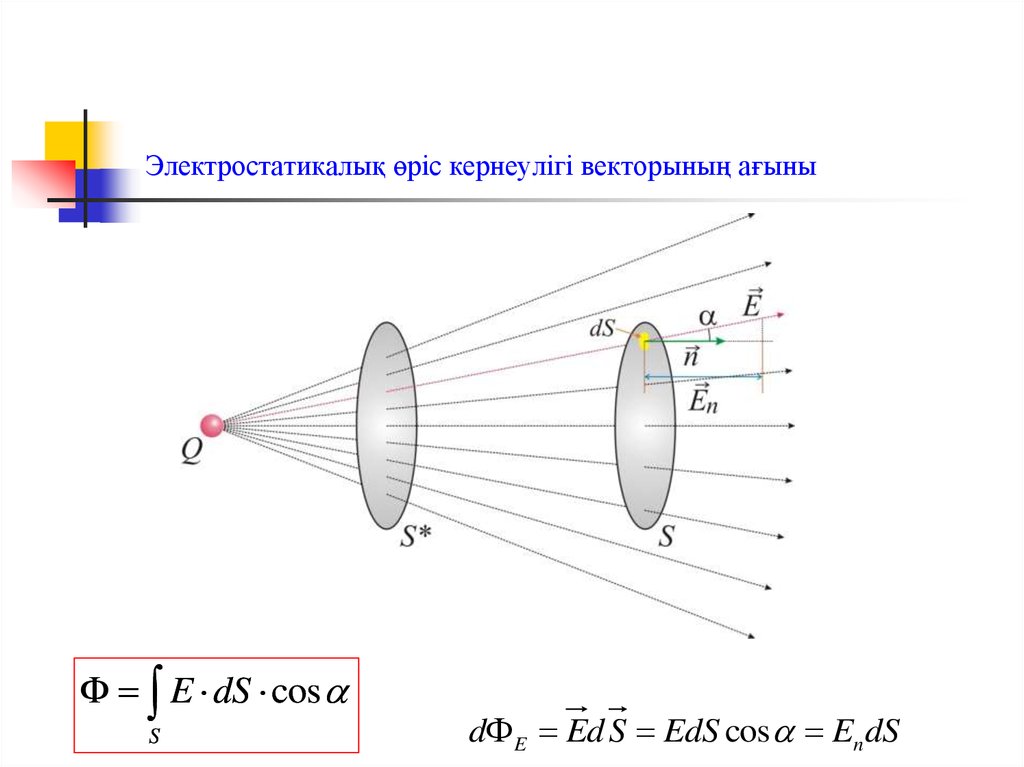
4. Электростатикалық өріс кернеулігі векторының ағыны
E dS cosS
d E Ed S EdS cos En dS
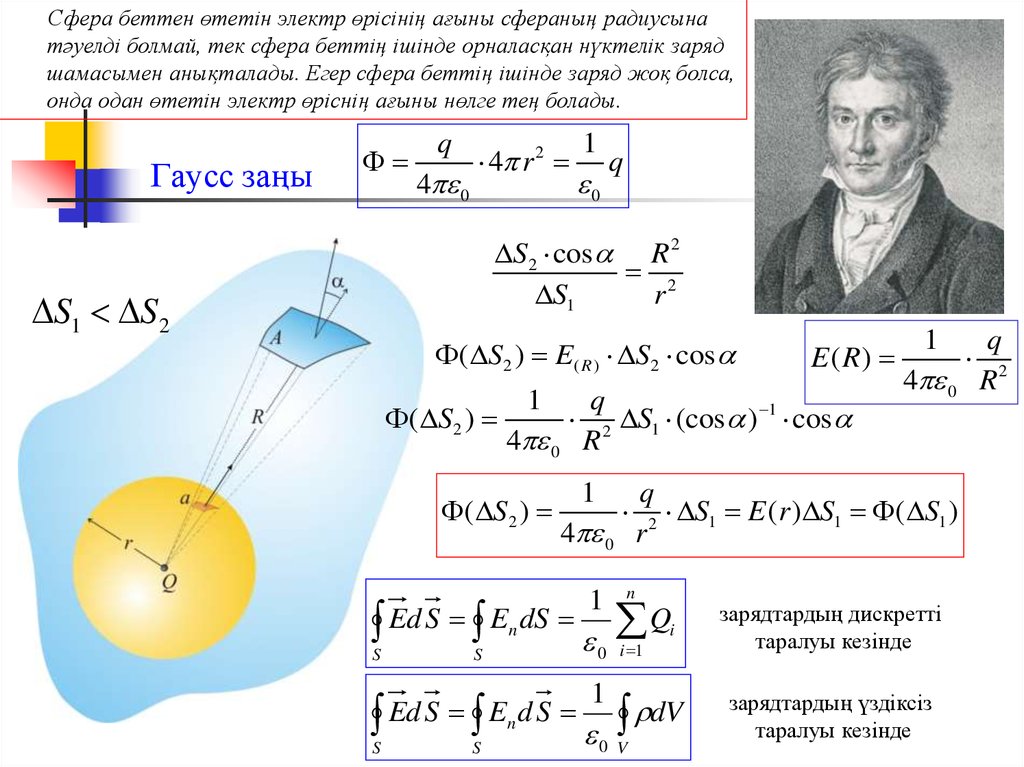
5. Гаусс заңы
Сфера беттен өтетін электр өрісінің ағыны сфераның радиусынатәуелді болмай, тек сфера беттің ішінде орналасқан нүктелік заряд
шамасымен анықталады. Егер сфера беттің ішінде заряд жоқ болса,
онда одан өтетін электр өріснің ағыны нөлге тең болады.
Гаусс заңы
q
4 0
4 r 2
1
0
q
S2 cos R 2
2
S1
r
S1 S2
( S2 ) E( R ) S2 cos
( S2 )
1
4 0
( S2 )
q
1
S
(cos
)
cos
1
2
R
1
4 0
1
S
S
Ed S En d S
n
S
S
0 i 1
1
i
dV
0 V
1
4 0
q
S1 E ( r ) S1 ( S1 )
2
r
Ed S E dS Q
n
E ( R)
зарядтардың дискретті
таралуы кезінде
зарядтардың үздіксіз
таралуы кезінде
q
R2
6. Қорытынды
- Кез-келген тұйық бет арқылы өтетін электростатикалық өрістің ағыны оның ішіндеорналасқан зарядтардың шамасымен (алгебралық қосындысымен анықталады), оның
пішініне, өлшеміне тәуелді болмайды.
- Электростатикалық өрістің көзі - заряд.
Гаусс
теоремасы,
біріншіден,
зарядтардың
өзара
әсерлері
олардың
арақашықтықтарының квадратына кері пропорционал екендігіне, екіншіден,
тәуелсіздік принципіне негізделген. Кулон заңы мен Гаусс теоремасы өзара балама.
-Кулон заңының көмегімен берілген тыныштықтағы зарядтар жүйесінің электр өрісін
анықтауға болады. Ал, Гаусс теоремасы арқылы өріс нүктелеріндегі кернеуліктерді біле
отырып, зарядтың шамасын анықтауға болады.
7. Өрістің дивергенциясы. Өріс көзі және құйылысы.
Беттің бірлік нормалы n ретінде сыртқа бағытталған нормальдыаламыз. Сонда беттің ішіне тұрғызылған нормаль теріс мән
қабылдайды.
dS
n
S
Егер тұйық бет S сығылмайтын сұйық ағынының ішінде орналасқан, ал
сұйық молекулаларының орташа жылдамдығы десек, онда мынадай
жағдайлар болуы мүмкін:
- S тұйық бетіне кірген сұйық мөлшері одан шыққан сұйық мөлшеріне тең болса, онда тұйық
беттен шығатын агығ нөлге тең болады. 0
- Тұйық бет ішінде сұйық молекулаларын жасап шығаратын көз, мысалы мұз болса, онда тұйық
бетке ағып кіретін су молекулаларының саны одан ағып шығатын су молекулаларының санынан
кем болып, тұйық беттен шығатын ағын оң мән қабылдайды. 0
-Тұйық бет ішінде енген су молекулаларын “жұтатын ” орталықтар болса, онда тұйық бет ішіне
ағып кірген су молекулаларының саны одан ағып шығатын сандарынан артық болып, тұйық
беттен шығатын ағын теріс қабылдайды. 0
Сонымен, тұйық бет ішінде су молекулаларын “тудыратын” көз, не оны “жұтатын” құйылыс
болса, одан ағып шығатын ағын не оң, не теріс мән қабылдайды. Көз бен құйылыстың қуаттарын
дивергенция деп атайды.
1
div
p lim
VS
n
dS
8. Остоградский –Гаусс теоремасы және оның дифференциалдық түрі.
Өріс көзінің қуаты мен ағының арасындағы байланысты табайық.(div ) V dS
(div )i Vi i dS
i
Si
idS dS
i
Si
S
i
i
Si
lim (div )i Vi div dV
Vi 0
div dV dS
V
i
i
i
V
Остоградский-Гаусс
теоремасы
S
Остоградский-Гаусс теоремасы векторлар өрісінің дивергенциясынан көлем бойынша алынған
интегралын осы көлемді қоршап тұрған тұйық бет арқылы ағып өтетін ағын шамасымен
байланыстырады.
E dS div E dV E dS dV div E dV dV
div E
1
0
Бұл Остоградский-Гаусс теоремасының электростатикалық өріс
дифференциалдық түрі. Яғни, Кулон заңының диффренциалдық түрі.
үшін
жазылған
S
V
S
1
0 V
V
1
0 V
9. Зат бөлшектерінің толқындық қасиеттері. Де Бройль жорамалы. Де Бройль жорамалының тәжірибеде расталуы.
Де Бройль гипотезасыТолқындық теория тұрғысынан қарағанда жарық
тербеліс жиілігі мен толқын ұзындығы арқылы
сипатталады. Корпускулалық теория бойынша жарық
фотонының ф энергиясы, mф массасы мен рф импульсы
мынаған тең:
2
, m 2 2 , p m c
.
c
c
c
Жарық фотонының импульсы мен жарық толқыны
ұзындығы арасындағы байланыс Планк тұрақтысы
арқылы өрнектеледі.
10.
Қозғалыстағы кез келген бөлшекпен бір толқындық процессбайланысқан болады.
2
де-Бройль теңдеулері
E , p k
де-Бройль толқын ұзындығы
.
2 / p 2 /( m ).
Электрон энергиясы Е=100 эВ болсын.
p m 2eUm
2 / p 2 / 2eUm .
Осындай электрон үшін де Бройль толқын ұзындығын есептейік.
Электрон жылдамдығы мына теңдіктен еU=m 2/2 анықталады:
5,93 105 U 5,93 106 м / с
ал толқын ұзындығы
2
6,62 10 34
1,2 10 10 м 0,12 нм.
31
6
m
9,1 10 5,93 10
11.
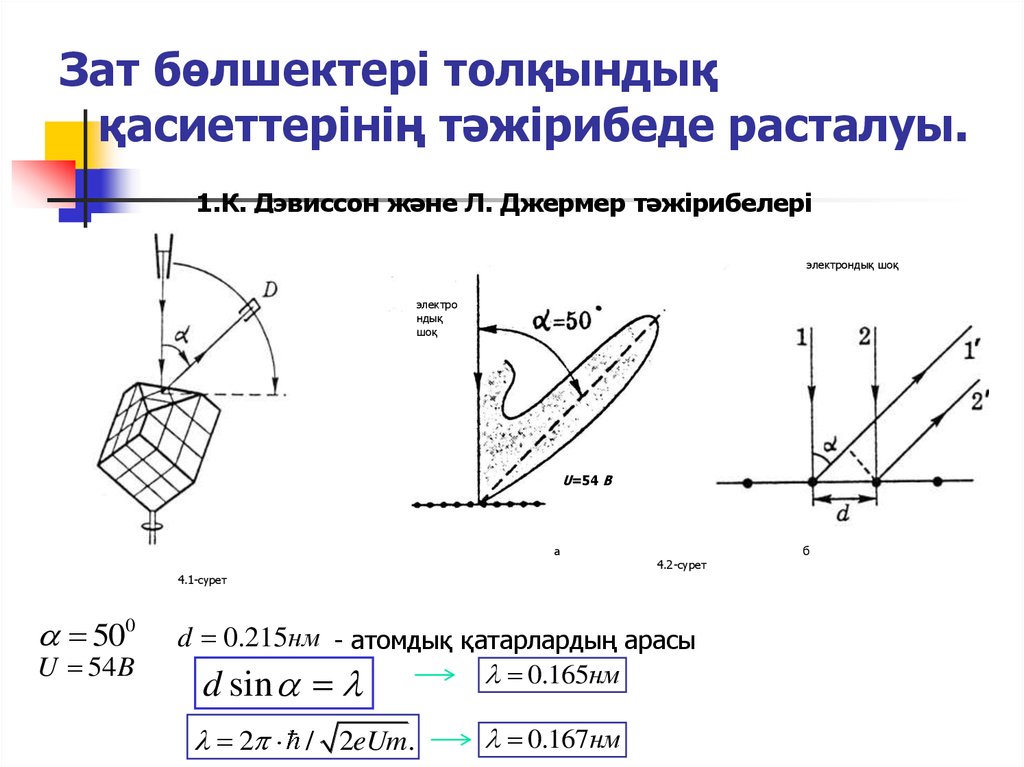
Зат бөлшектері толқындыққасиеттерінің тәжірибеде расталуы.
1.К. Дэвиссон және Л. Джермер тәжірибелері
электрондық шоқ
электро
ндық
шоқ
U=54 B
а
4.2-сурет
4.1-сурет
500
U 54 B
d 0.215нм - атомдық қатарлардың арасы
0.165нм
d sin
2 / 2eUm.
0.167нм
б
12. Дэвиссон мен Джермердің никель монокристалымен жүргізген (=80, d=0,203 нм) тәжірибелерінде алынған қисық келтірілген.
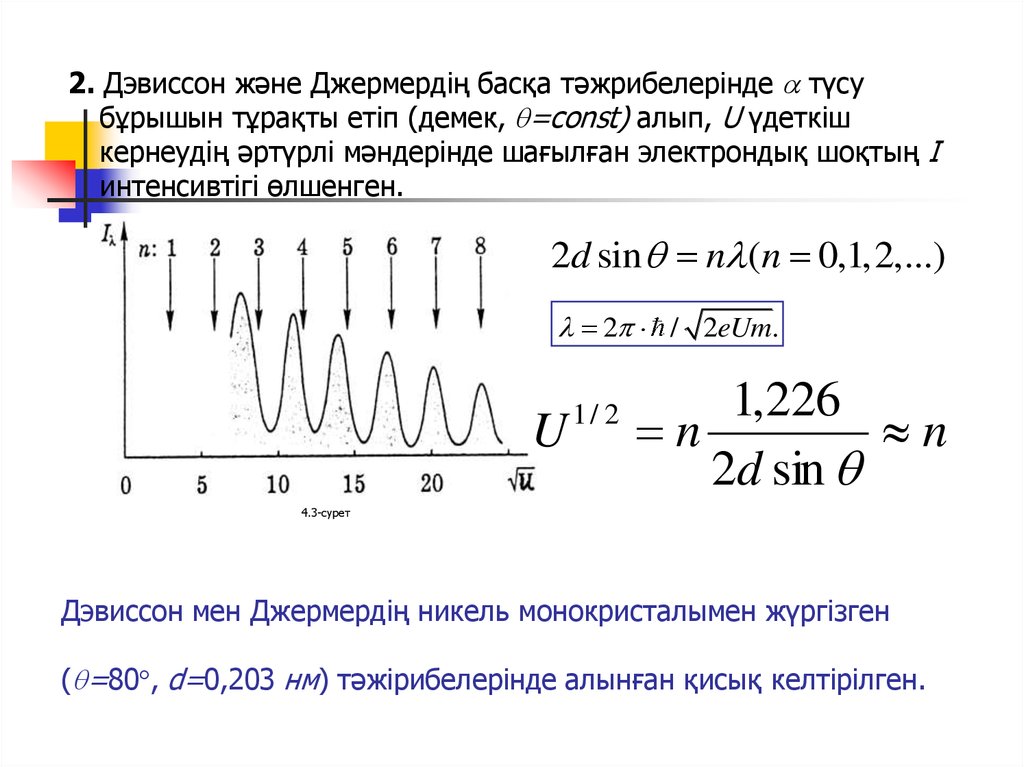
2. Дэвиссон және Джермердің басқа тәжрибелерінде түсубұрышын тұрақты етіп (демек, =const) алып, U үдеткіш
кернеудің әртүрлі мәндерінде шағылған электрондық шоқтың І
интенсивтігі өлшенген.
2d sin n (n 0,1,2,...)
2 / 2eUm.
U
1/ 2
1,226
n
n
2d sin
4.3-сурет
Дэвиссон мен Джермердің никель монокристалымен жүргізген
( =80 , d=0,203 нм) тәжірибелерінде алынған қисық келтірілген.
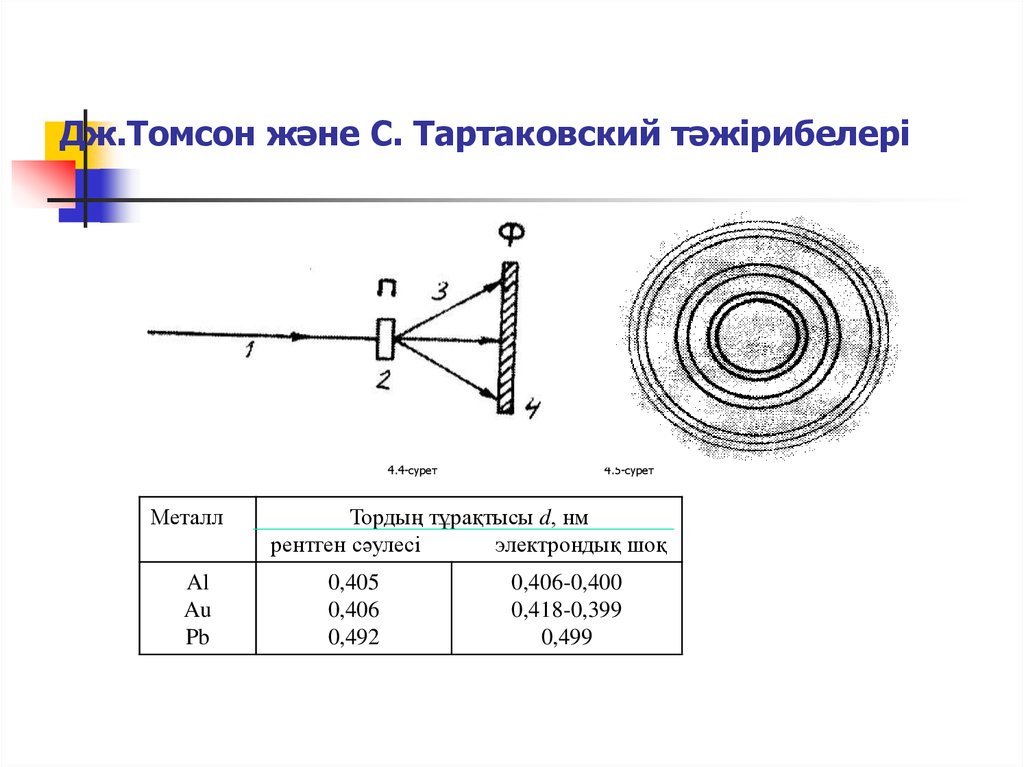
13. Дж.Томсон және С. Тартаковский тәжірибелері
4.4-суретМеталл
Al
Au
Pb
4.5-сурет
Тордың тұрақтысы d, нм
рентген сәулесі
электрондық шоқ
0,405
0,406
0,492
0,406-0,400
0,418-0,399
0,499
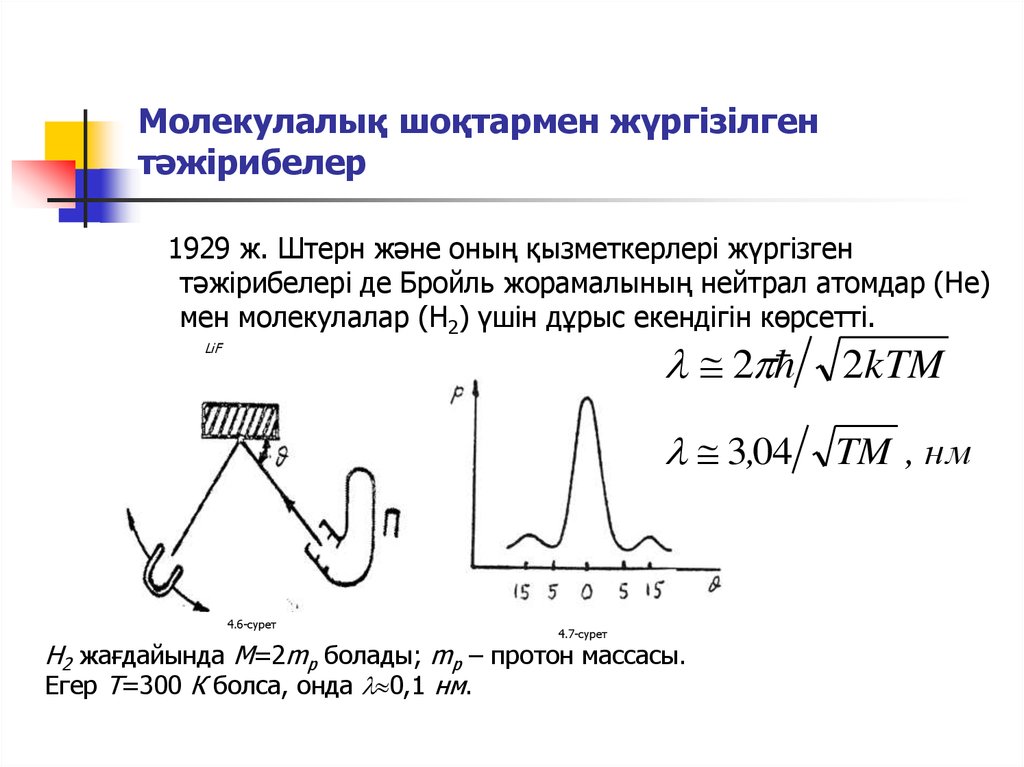
14. Молекулалық шоқтармен жүргізілген тәжірибелер
1929 ж. Штерн және оның қызметкерлері жүргізгентәжірибелері де Бройль жорамалының нейтрал атомдар (Не)
мен молекулалар (Н2) үшін дұрыс екендігін көрсетті.
LіF
4.6-сурет
4.7-сурет
2
2kTM
3,04
TM , нм
Н2 жағдайында М=2mp болады; mp – протон массасы.
Егер Т=300 К болса, онда 0,1 нм.







 physics
physics








