Переменные величины и их свойства

1. Раздел IV Введение в математический анализ Глава 1 Функция

Параграф 1
Переменные величины и их
свойства
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

2. Под величиной понимают все то, что может быть измерено и выражено числом (числами). Переменной величиной называют величину,

которая принимает различные
численные значения; величина, которая
сохраняет одно и тоже численное
значение, называется постоянной.

3. Переменная величина считается заданной, если задана совокупность её значений. Совокупность значений переменной величины

называется областью изменения переменной
величины.

4. Переменная величина называется непрерывной, если областью её изменения является некоторый интервал. Переменная величина

называется дискретной, если
областью её изменения является множество
изолированных точек.

5. Переменная величина называется упорядоченной, если из двух значений переменной величины можно указать предыдущую и последующую.

Если переменная величина в области изменения убывает
или возрастает, то она называется монотонной.
Если значения переменной величины таковы, что число
будет больше (меньше) любого значения переменной
величины, то говорят, что переменная величина
ограниченна сверху (снизу). Переменная величина
называется ограниченной, если она ограничена сверху и
снизу.

6. Раздел IV Введение в математический анализ Глава 1 Функция

Параграф 2
Функции одной и нескольких
переменных
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

7. Чаще всего изменению одной переменной величины сопутствует изменение другой, более того, изменение одной является причиной

изменения другой. В некоторых случаях
изменение одной переменной величины может
быть продиктовано изменением двух, трех и
более величин.

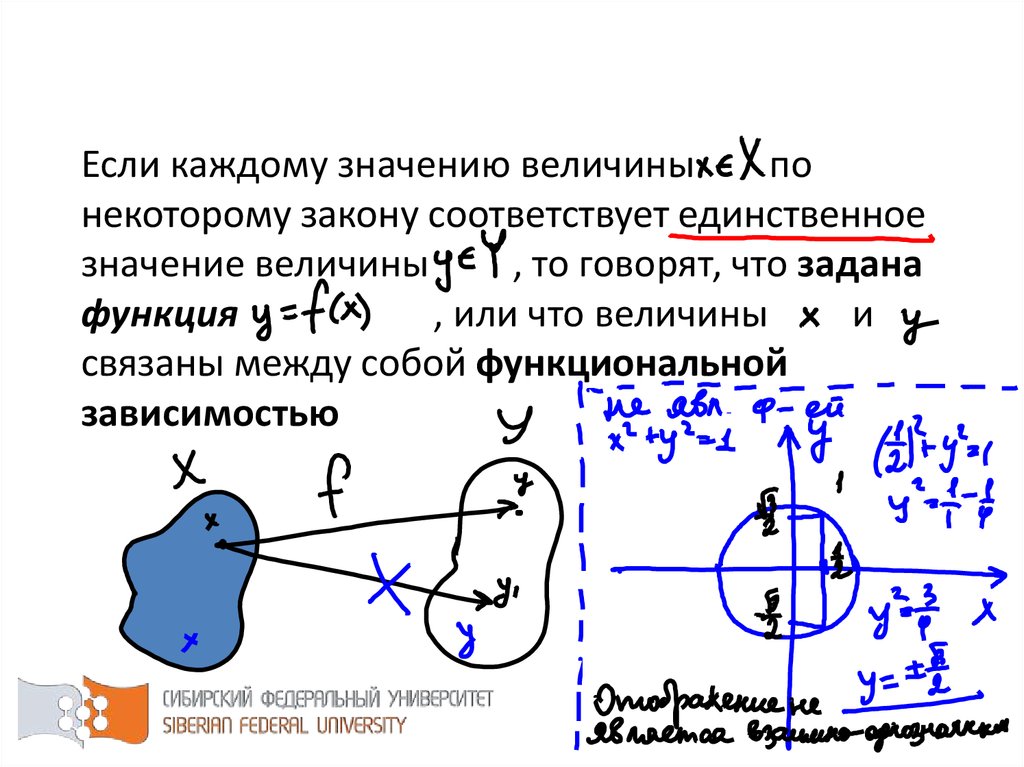
8. Если каждому значению величины по некоторому закону соответствует единственное значение величины , то говорят, что задана

функция
, или что величины
и
связаны между собой функциональной
зависимостью

9. При этом, – аргумент функции (независимая переменная), – значение функции (зависимая переменная), – закон соответствия, –

функция одной независимой
переменной.

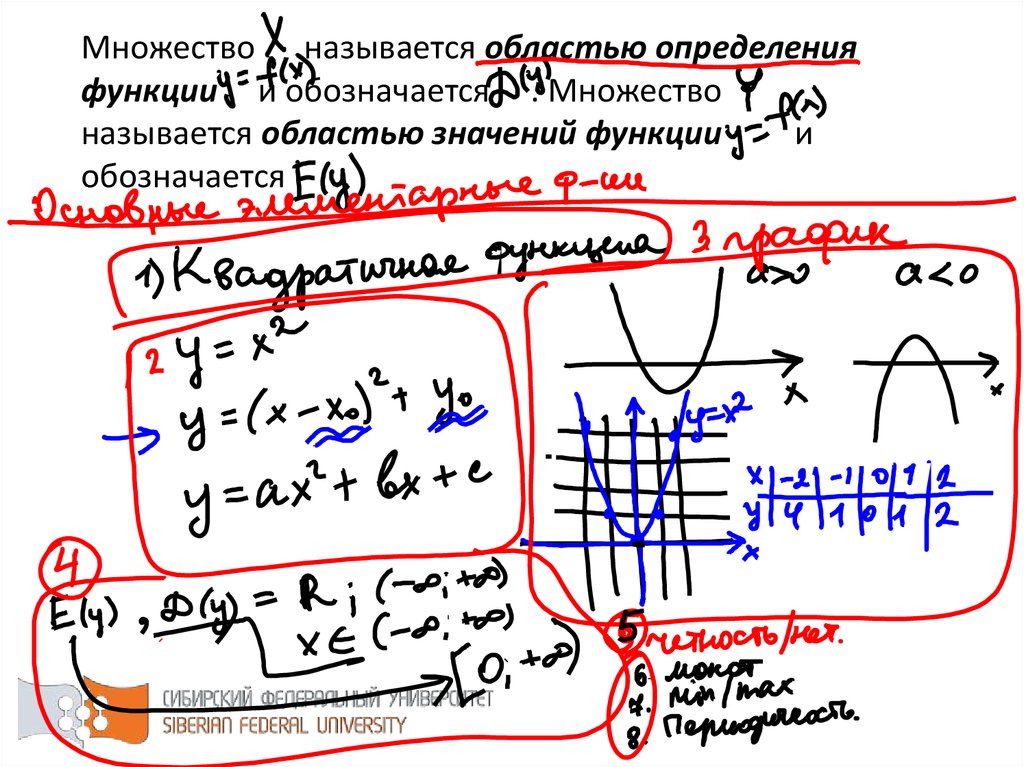
10. Множество называется областью определения функции и обозначается . Множество называется областью значений функции и

обозначается
.

11. Для функции одной переменной областью определения является интервал координатной оси или вся координатная ось.

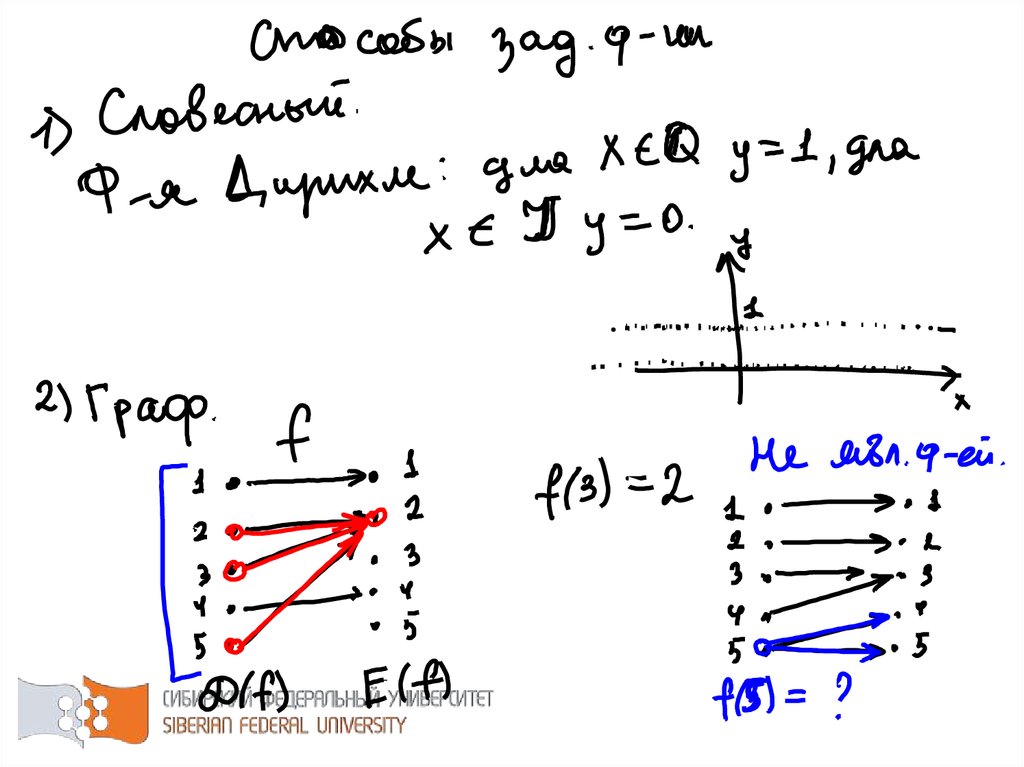
12. Если каждой паре чисел по некоторому закону соответствует единственное значение величины , то говорят, что задана функция

Если каждой паре чисел по некоторому закону
соответствует единственное значение величины
говорят, что задана функция
, то

13. При этом – аргументы функции (независимые переменные), – значение функции (зависимая переменная), – закон соответствия, –

функция двух независимых переменных,
– область определения функции,
– область значений функции.

14. Для функции двух переменных область определения является часть координатной плоскости или вся координатная плоскость.

15.

16.

17.

18.

СВОЙСТВА ФУНКЦИИ
1. Непрерывность
2. Четность
3. Периодичность
4. Нули функции
5. Промежутки знакопостоянства
6. Монотонность
7. Экстремумы функции
8. Точки перегиба. Выпуклость

19.

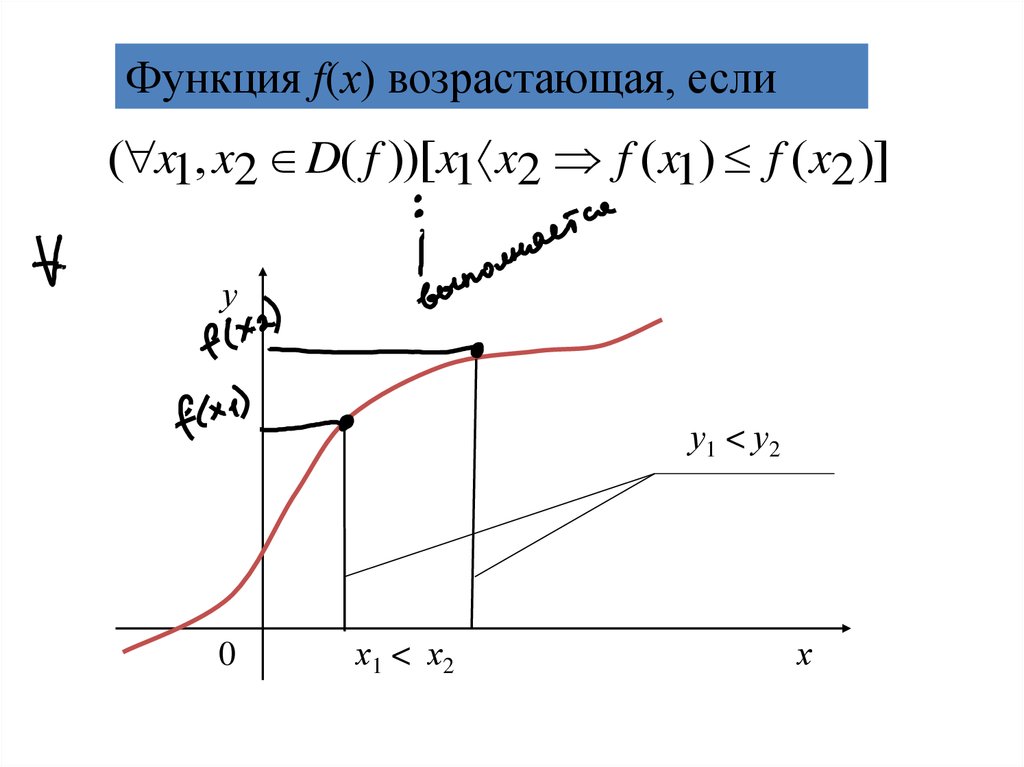
Функция f(х) возрастающая, если
( x1, x2 D( f ))[x1 x2 f ( x1) f ( x2 )]
у
у1 < у2
0
х1 < х2
х

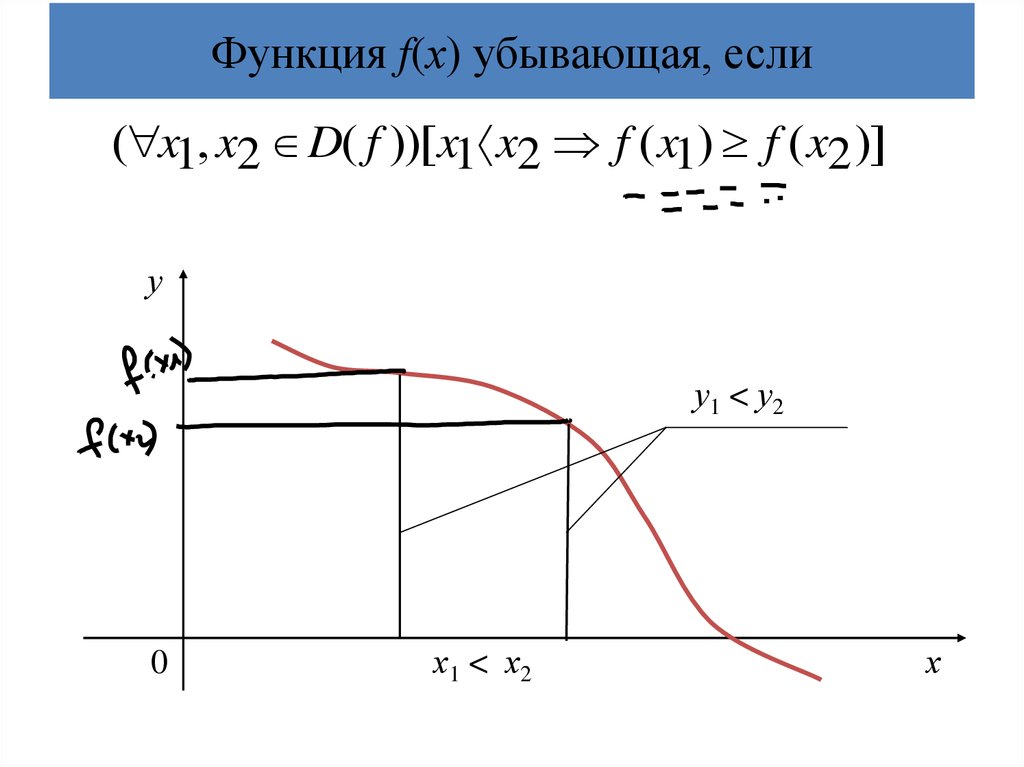
20. Функция f(х) убывающая, если

( x1, x2 D( f ))[ x1 x2 f ( x1) f ( x2 )]
у
у1 < у2
0
х1 < х2
х

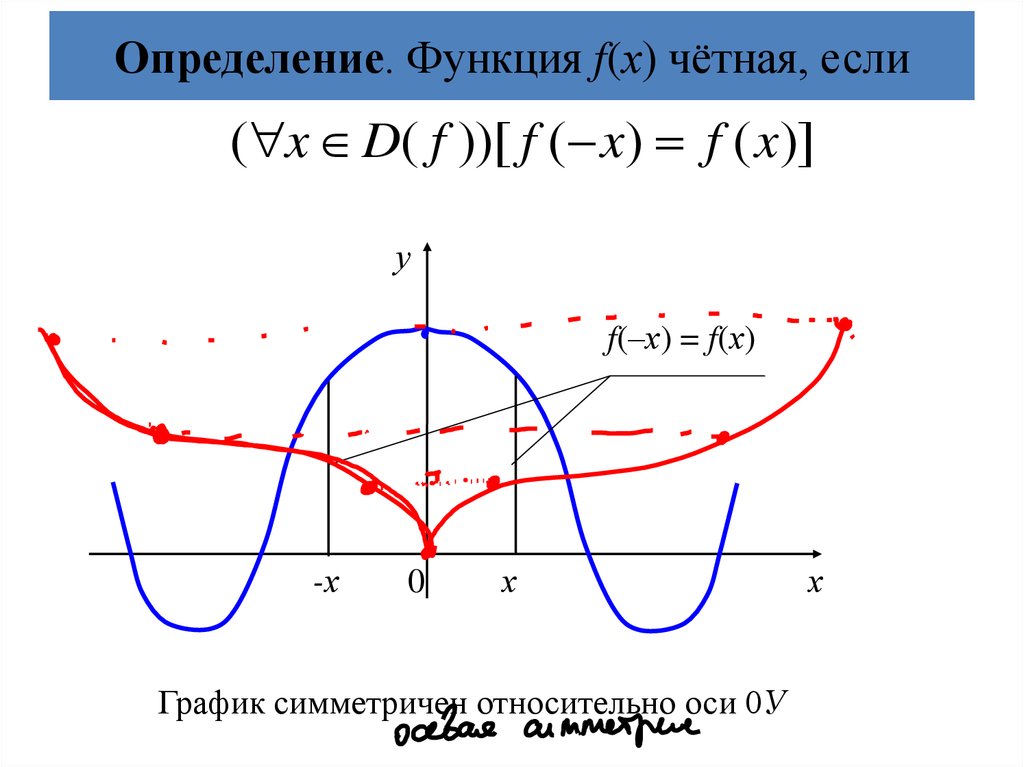
21. Определение. Функция f(х) чётная, если

( x D( f ))[ f ( x) f ( x)]
у
f(–х) = f(х)
-х
0
х
График симметричен относительно оси 0У
х

22. Определение. Функция f(х) нечётная, если

( x D( f ))[ f ( x) f ( x)]
у
f(–х) = –f(х)
-х
0
х
График симметричен относительно точки 0

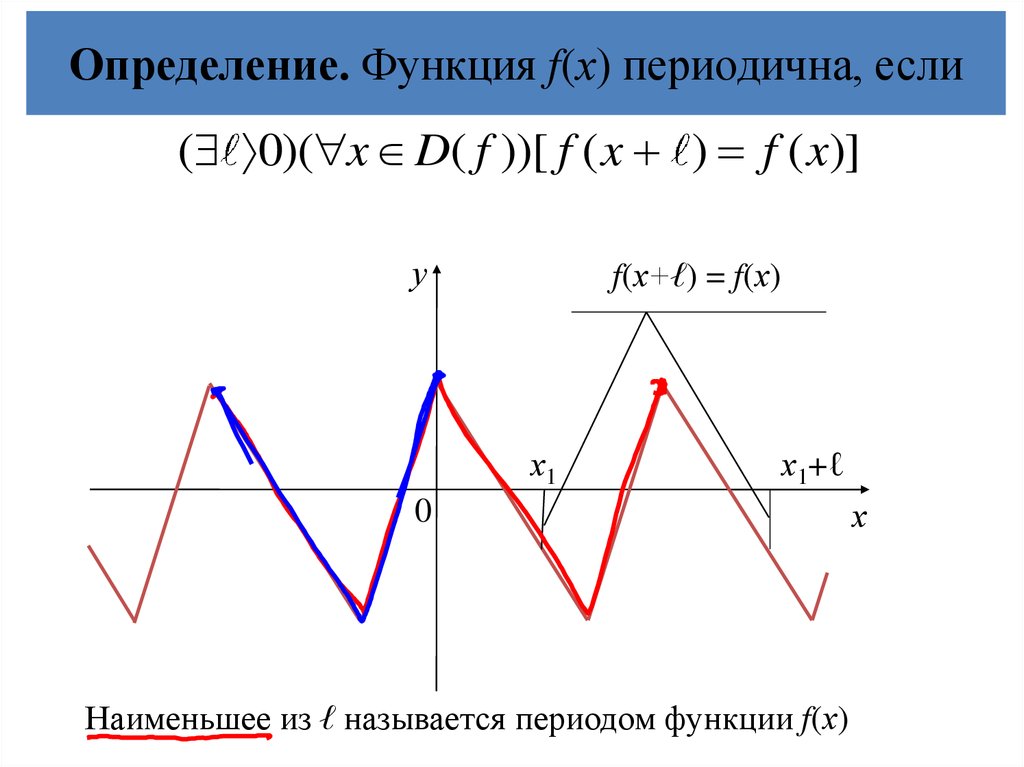
23. Определение. Функция f(х) периодична, если

( 0)( x D( f ))[ f ( x ) f ( x)]
у
f(х+ℓ) = f(х)
х1
х1+ℓ
0
Наименьшее из ℓ называется периодом функции f(х)
х

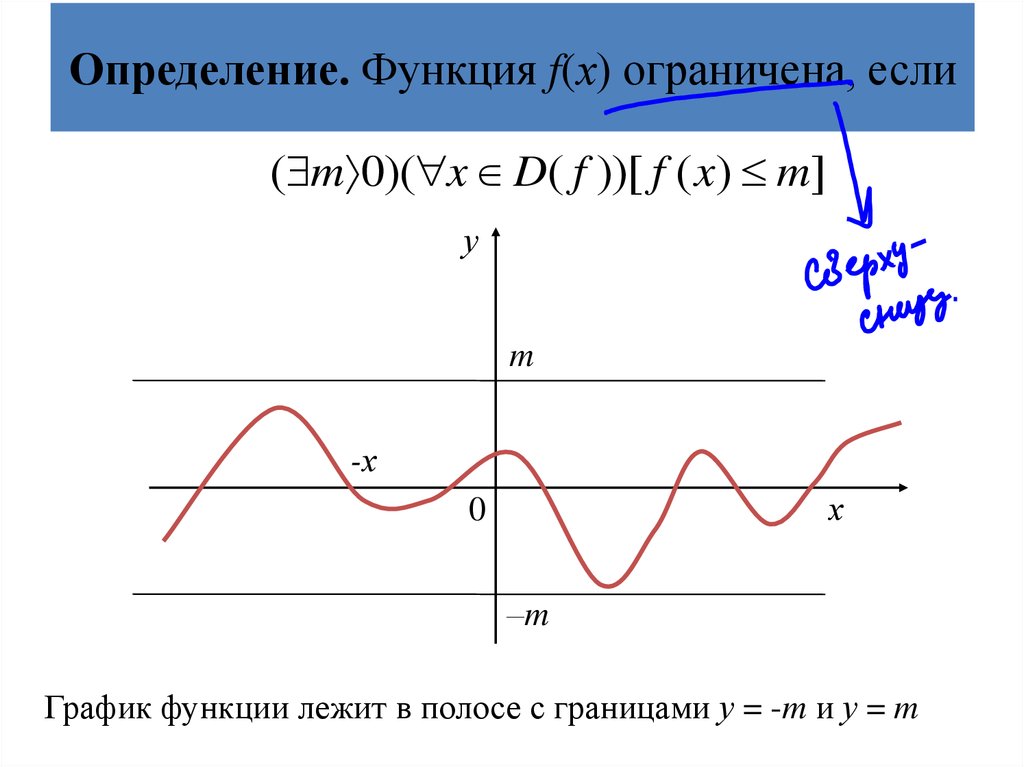
24. Определение. Функция f(х) ограничена, если

( m 0)( x D( f ))[ f ( x) m]
у
m
-х
х
0
–m
График функции лежит в полосе с границами у = -m и у = m

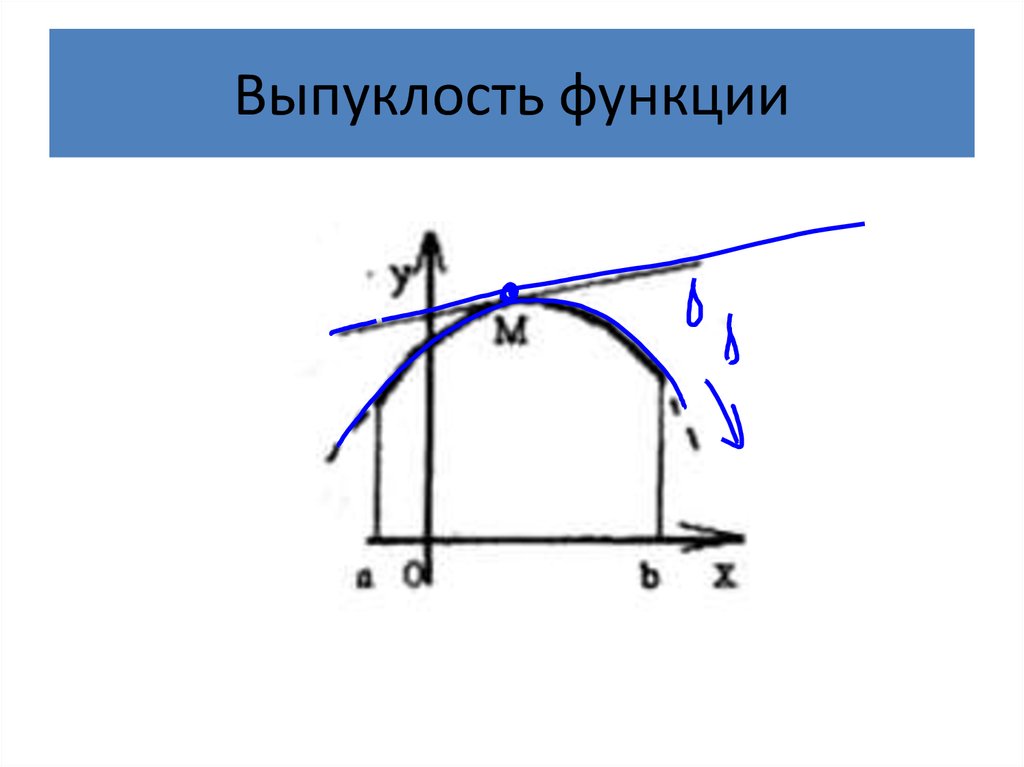
25. Выпуклость функции

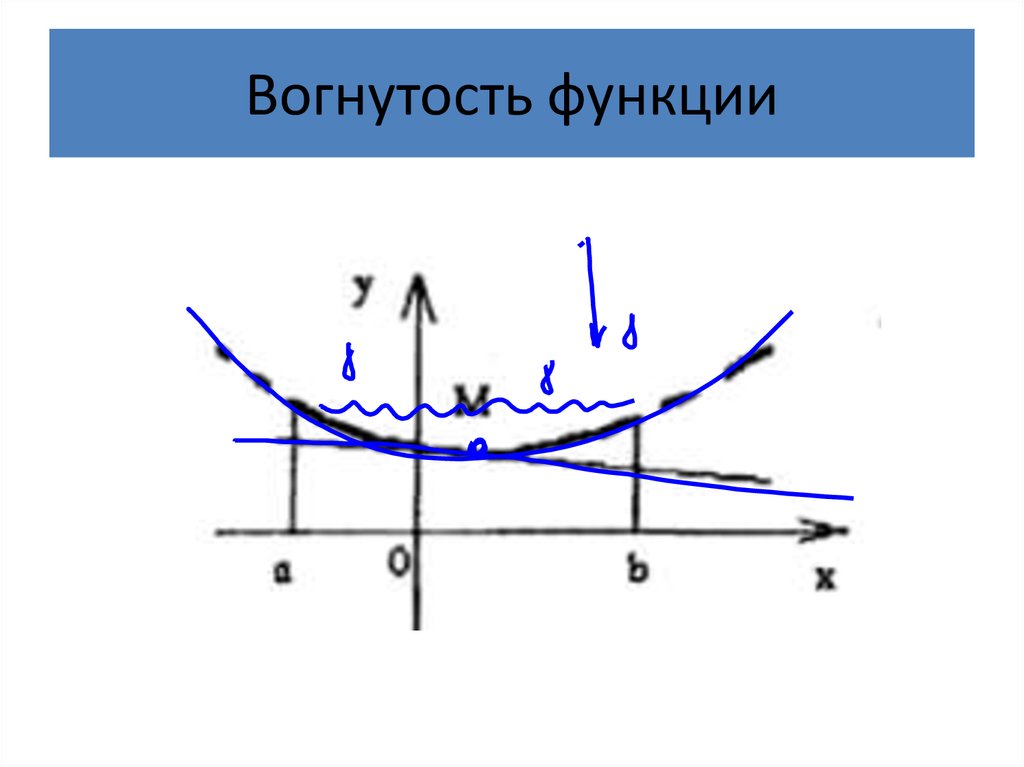
26. Вогнутость функции

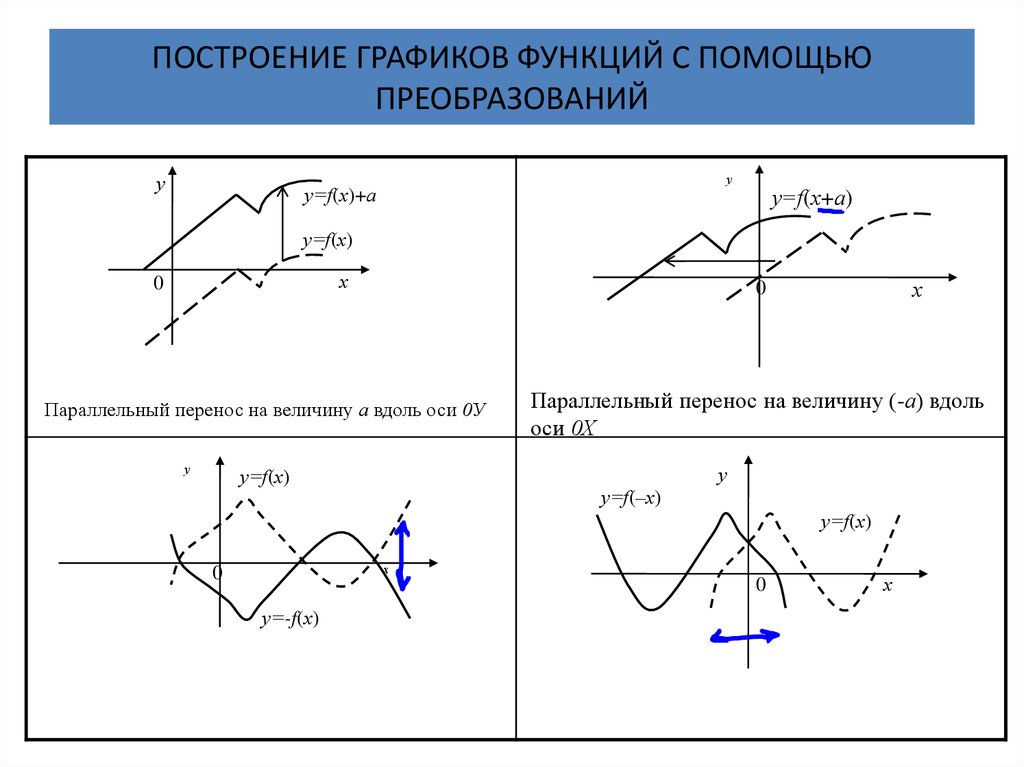
27. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЙ

у
у
у=f(х)+а
у=f(х+а)
у=f(х)
х
0
Параллельный перенос на величину а вдоль оси 0У
у
х
0
Параллельный перенос на величину (-а) вдоль
оси 0Х
у
у=f(х)
у=f(–х)
у=f(х)
х
0
0
у=-f(х)
х

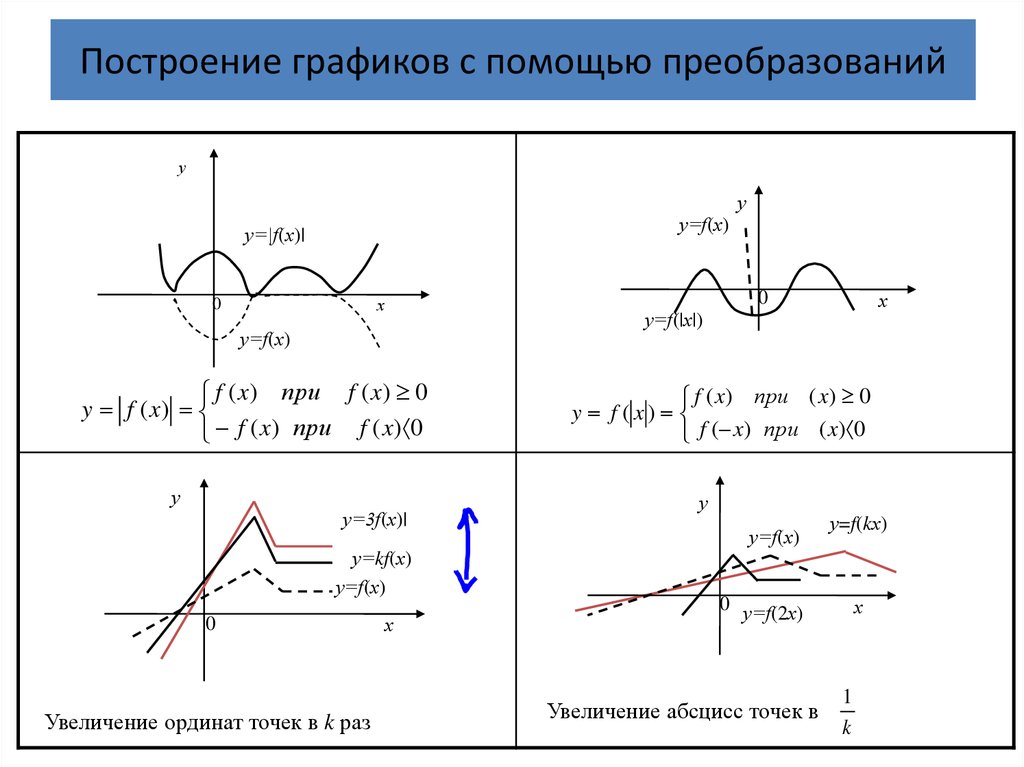
28. Построение графиков с помощью преобразований

у
у=f(х)
у=|f(х)|
х
0
у=f(х)
f ( x) при f ( x) 0
y f ( x)
f ( x) при f ( x) 0
у
у=3f(х)|
у=kf(х)
у=f(х)
0
Увеличение ординат точек в k раз
х
у
х
0
у=f(|х|)
f ( x) при ( x) 0
y f ( x)
f ( x) при ( x) 0
у
у=f(х)
у=f(kх)
х
0 у=f(2х)
Увеличение абсцисс точек в
1
k

29.

30.

31.

32.

33.

34.

35.

36.

37. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 1
Предел переменной величины
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

38. Если значения переменной величины в процессе её изменения как угодно близко приближаются к некоторому числу , то говорят, что

переменная
величина стремится к а или предел переменной
величины равен а ,
обозначают x a
или lim x a .

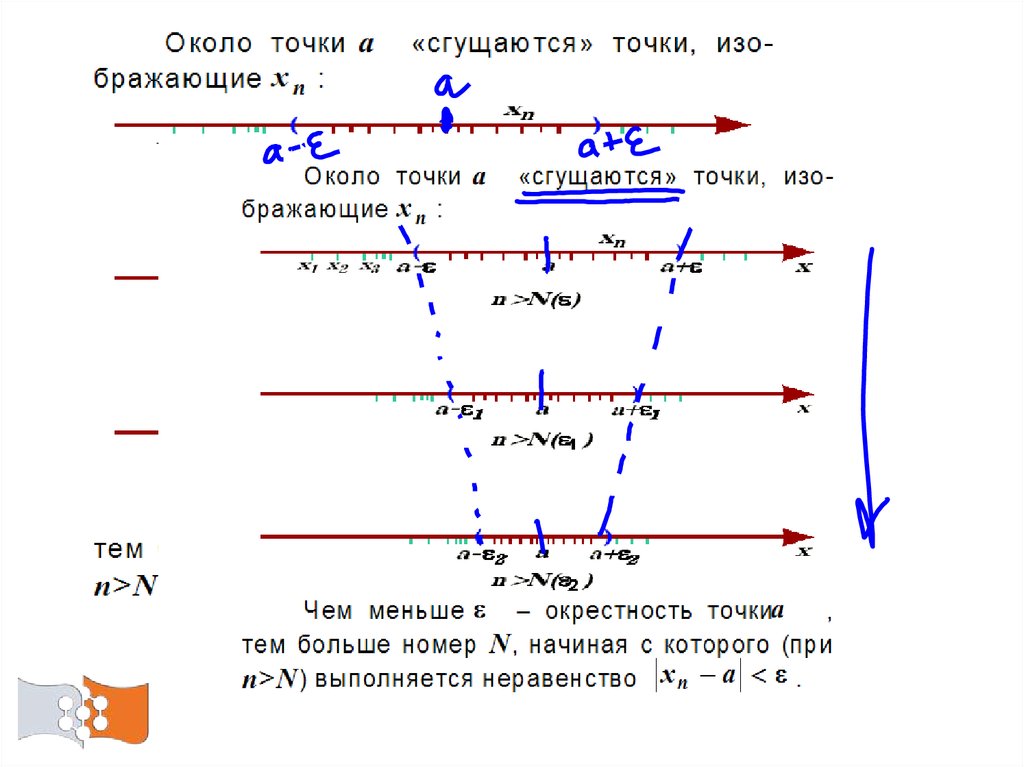
39. Пусть – некоторое значение переменной величины и – сколь угодно малое положительное число. Все точки интервала (кроме самой

точки ),
удовлетворяющие неравенству
,
образуют – окрестность точки.

40. Иначе говоря, если – предел переменной величины , то все значения переменной величины , большие , попадут в – окрестность точки

Предел переменной величины
Иначе говоря, если – предел переменной
величины
, то все значения переменной
величины
, большие
, попадут в
– окрестность точки
.

41. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 2
Предел последовательности
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

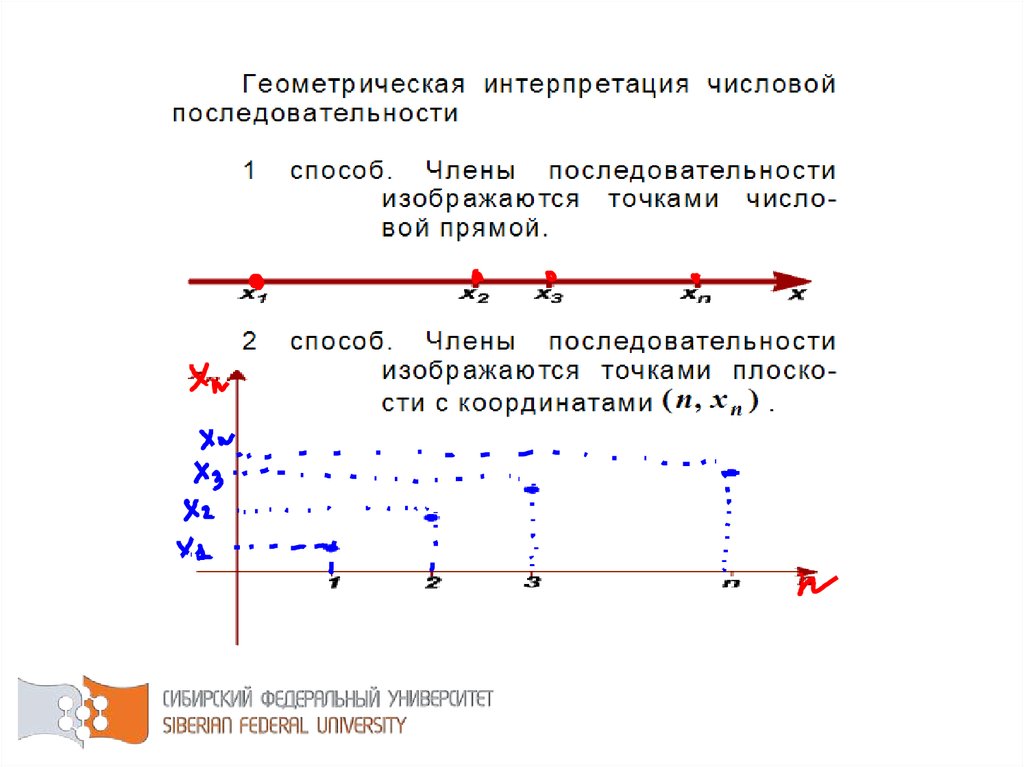
42.

43.

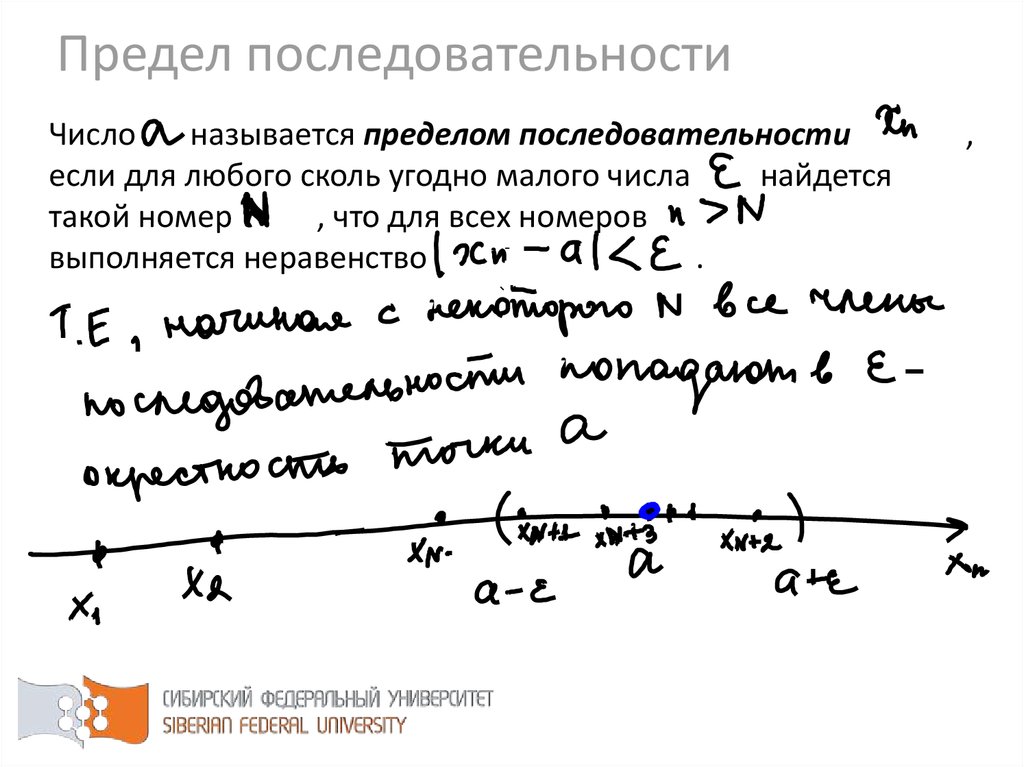
44. Число называется пределом последовательности , если для любого сколь угодно малого числа найдется такой номер , что для всех

Предел последовательности
Число
называется пределом последовательности
если для любого сколь угодно малого числа
найдется
такой номер
, что для всех номеров
выполняется неравенство
.
,

45. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 3
Предел функции одной
переменной
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

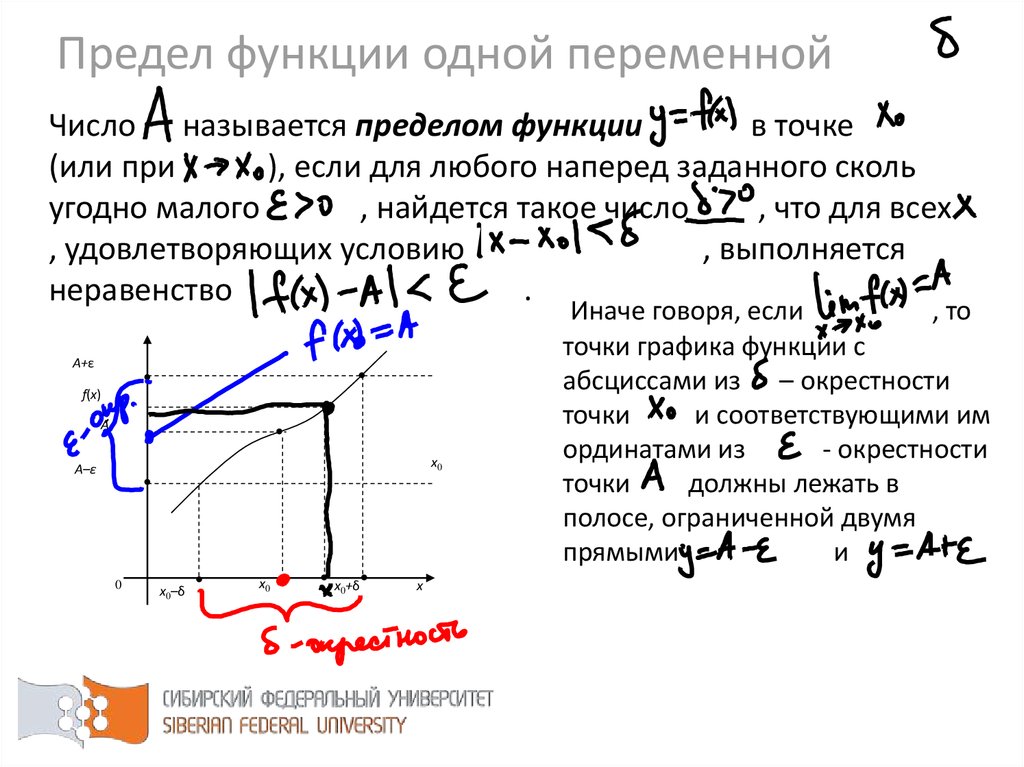
46. Число называется пределом функции в точке (или при ), если для любого наперед заданного сколь угодно малого , найдется такое

Предел функции одной переменной
Число называется пределом функции
в точке
(или при
), если для любого наперед заданного сколь
угодно малого
, найдется такое число
, что для всех
, удовлетворяющих условию
, выполняется
неравенство
.
A+ε
f(x)
A
x0
A–ε
0
x0–δ
x0
x0+δ
x
Иначе говоря, если
, то
точки графика функции с
абсциссами из – окрестности
точки
и соответствующими им
ординатами из
- окрестности
точки
должны лежать в
полосе, ограниченной двумя
прямыми
и

47.

Предел функции в бесконечной точке

48. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 4
Односторонние пределы
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

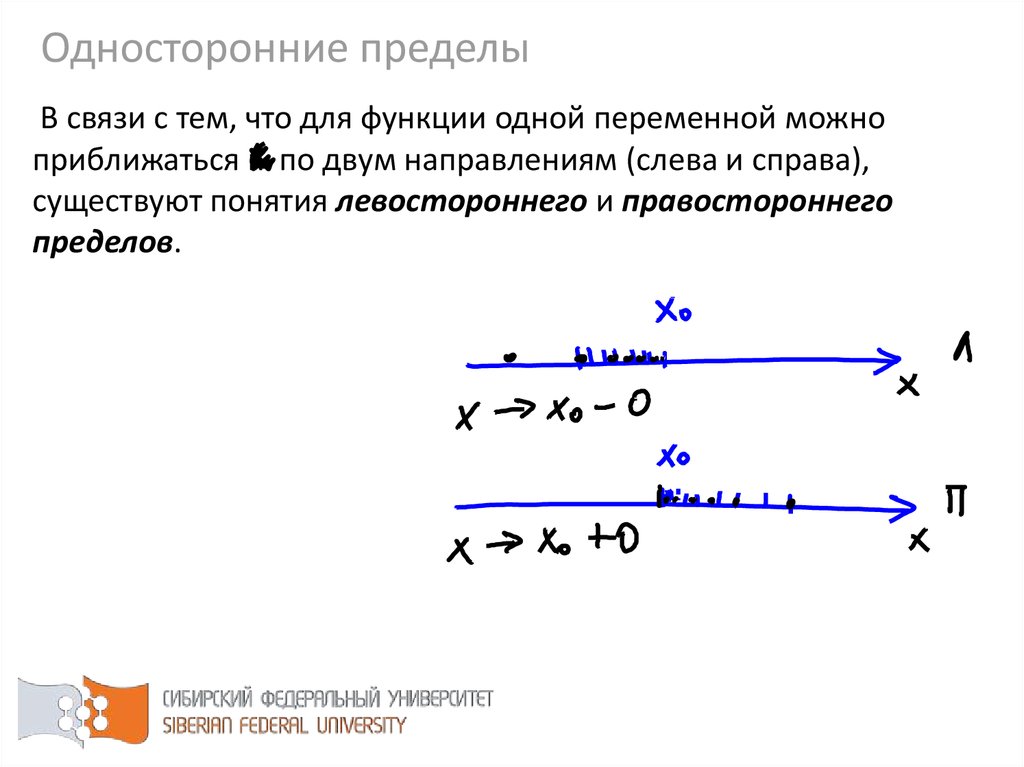
49. В связи с тем, что для функции одной переменной можно приближаться к по двум направлениям (слева и справа), существуют понятия

Односторонние пределы
В связи с тем, что для функции одной переменной можно
приближаться к по двум направлениям (слева и справа),
существуют понятия левостороннего и правостороннего
пределов.

50. Число называется левосторонним пределом функции в точке , если для любого сколь угодно малого наперед заданного числа ,

Односторонние пределы
Число называется левосторонним пределом функции в
точке ,
если для любого сколь угодно малого наперед
заданного числа
, найдется такое число
, что при
выполняется неравенство
.
Иначе говоря, если слева (оставаясь меньше ), то предел
функции
– левосторонний, записывается в
виде
.
Число называется правосторонним пределом функции
в точке
, если для любого сколь угодно малого наперед
заданного числа
, найдется такое число
, что при
выполняется неравенство
.
Иначе говоря, если справа (оставаясь больше ), то предел
функции
– правосторонний, записывается в виде
.

51.

Односторонние пределы

52. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 6
Бесконечно большие величины
Бесконечно малые величины
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

53.

54.

55.

56.

57. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 7
Замечательные пределы
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

58.

59.

60. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 8
Точки разрыва функции и их
классификация
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

61. Функция в точке может быть непрерывна, терпеть устранимый разрыв (разрыв I рода), разрыв «скачек» (разрыв I рода), бесконечный

разрыв (разрыв II рода).

62.

63. Раздел IV Введение в математический анализ Глава 2 Пределы

Параграф 9
Приращение функции
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

64. Рассмотрим функцию одной переменной , определенную на некотором интервале .

Приращение функции одной переменной
Рассмотрим функцию одной переменной
определенную на некотором интервале
,
.

65. Рассмотрим функцию двух переменных , определенную на в некоторой области .

Приращение функции двух переменных
Рассмотрим функцию двух переменных
определенную на в некоторой области
,
.

66. Раздел IV Введение в математический анализ Глава 3 Производная и дифференциал

Параграф 1
Основные определения
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

67.

68.

69.

70.

71.

72. Раздел IV Введение в математический анализ Глава 3 Производная и дифференциал

Параграф 2
Правила вычисления производных
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

73.

74. Раздел IV Введение в математический анализ Глава 3 Производная и дифференциал

Параграф 3
Физический (механический) смысл
производных
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

75.

76. Раздел IV Введение в математический анализ Глава 3 Производная и дифференциал

Параграф 4
Геометрический смысл
производных
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

77.

y
M
α
x
0
Рис.2.3.3

78. Раздел IV Введение в математический анализ Глава 3 Производная и дифференциал

Параграф 4
Производная неявно заданной
функции
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ

79. Раздел IV Введение в математический анализ Глава 3 Производная и дифференциал

Параграф 5
Производная параметрически
заданной функции
к.п.н. Безотечество Мила Михайловна,
кафедра ФЕО ИЦМиМ СФУ