Дискретные, непрерывные случайные величины

1. МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ Государственное автономное образовательное учреждение Астраханской

области высшего образования
«АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
(ГАОУ АО ВО «АГАСУ»)
КОЛЛЕДЖ СТРОИТЕЛЬСТВА И ЭКОНОМИГИ АГАСУ
ПРЕЗЕНТАЦИЯ
По дисциплине: «Теория вероятности»
На тему: «Дискретные, непрерывные случайные величины»
Выполнил студент группы ИС-21-18:
Шолыхов А. Е.
Проверил преподаватель:
Терновая Г. Н.
г. Астрахань
2020

2. Случайной величиной называется величина, которая в результате опыта может принимать то или иное числовое значение, причем

заранее неизвестно какое
именно.
Обозначают
· случайные величины заглавными буквами латинского алфавита: X, Y, Z, U, V …
· значения случайных величин малыми буквами с индексами: x1, x2,…y1, y2,…
Примеры случайных величин:
1) X – число попаданий в мишень при двух выстрелах;
возможные значения этой СВ: x1 = 0 (нет ни одного попадания), x2 = 1 (одно
попадание), x3 = 2 (два попадания).
2) Y – рост случайно выбранного человека;
Возможные значения СВ Y перечислить нельзя, можно лишь указать промежуток,
которому эти значения принадлежат: ymin – ymax.
Примеры 1) и 2) показывают, что случайные величины можно разделить на две
категории: те, которые принимают отдельные, изолированные значения на
числовой прямой и те, которые заполняют некоторый промежуток на числовой
прямой. Эти категории образуют Дискретные и Непрерывные случайные
величины.

3. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения

Дискретной случайной величиной называется такая величина, которая в результате опыта
может принимать определенные значения образующие счетное множество (множество,
элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной
случайной величиной, т.к. эта величина может принимать счетное, хотя и бесконечное
количество значений.

4. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или

Непрерывной случайной величиной называется такая величина, которая может принимать
любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо
также указать вероятность этого значения.

5. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной

Соотношение между возможными значениями случайной величины и их
вероятностями называется законом распределения дискретной случайной
величины.
Закон распределения может быть задан аналитически, в виде
таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей
называется рядом распределения.
Графическое представление этой таблицы называется многоугольником
распределения. При этом сумма все ординат многоугольника распределения
представляет собой вероятность всех возможных значений случайной величины,
а, следовательно, равна единице.

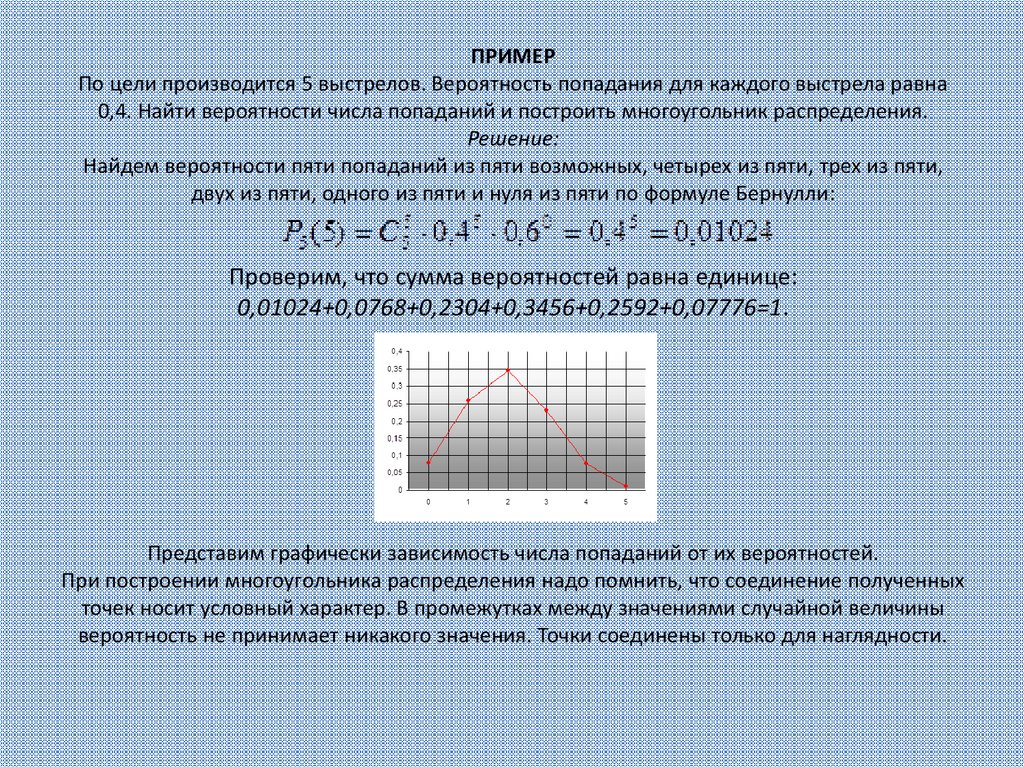
6. ПРИМЕР По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа

попаданий и построить многоугольник распределения.
Решение:
Найдем вероятности пяти попаданий из пяти возможных, четырех из пяти, трех из пяти,
двух из пяти, одного из пяти и нуля из пяти по формуле Бернулли:
Проверим, что сумма вероятностей равна единице:
0,01024+0,0768+0,2304+0,3456+0,2592+0,07776=1.
Представим графически зависимость числа попаданий от их вероятностей.
При построении многоугольника распределения надо помнить, что соединение полученных
точек носит условный характер. В промежутках между значениями случайной величины
вероятность не принимает никакого значения. Точки соединены только для наглядности.

7. Функция распределения случайной величины Функцией распределения называют функцию F(x), определяющую вероятность того, что

Функция распределения случайной величины
Функцией распределения называют функцию F(x), определяющую вероятность
того, что случайная величина Х в результате испытания примет значение,
меньшее аргумента х.
F(x)=P(X<x)
Функцию распределения также называют интегральной функцией.
Функция распределения существует как для непрерывных, так и для дискретных
случайных величин. Она полностью характеризует случайную величину и
является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:

8. Свойства функции распределения 1) значения функции распределения принадлежат отрезку [0, 1]. 0<F(x)<1  2) F(x) – неубывающая

Свойства функции распределения
1) значения функции распределения принадлежат отрезку [0, 1].
0<F(x)<1
2) F(x) – неубывающая функция:
при
F(x2)>F(x1)
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна
приращению функции распределения на этом интервале:
F(a<X<b)=F(a)-F(b)
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция
распределения равна единице:
F=0, F=1
5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение,
равна, нулю:
F(X=x0)=0
если X – непрерывная случайная величина.
Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины.
Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что
соответствует большинству практических задач.

9.   Плотностью распределения вероятностей непрерывной случайной величины Х называется первая производная от функции распределения

Плотностью распределения вероятностей непрерывной случайной величины Х
называется первая производная от функции распределения F(x):
функция f(x) – плотность распределения вероятностей.
Плотность распределения также называют дифференциальной функцией. Для
описания дискретной случайной величины плотность распределения
неприменима.
Смысл плотности распределения состоит в том, что она показывает как часто
появляется случайная величина Х в некоторой окрестности точки х при
повторении опытов.
После введения функций распределения и плотности распределения можно дать
следующее определение непрерывной случайной величины.

10. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность

Случайная величина Х называется непрерывной, если ее функция распределения
F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует
везде, за исключением, может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность с которой
некоторая случайная величина Х примет значение, принадлежащее заданному
интервалу.

11. Теорема Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна

определенному интегралу от
плотности распределения, взятому в пределах от a до b
Геометрически это означает, что вероятность того, что непрерывная случайная
величина примет значение, принадлежащее интервалу (a, b), равна площади
криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и
прямыми
x = a и x = b.
Функция распределения может быть найдена, если известна плотность
распределения, по формуле: