Переменная величина

1. ПЕРЕМЕННАЯ ВЕЛИЧИНА

•Y=f(x)
ПЕРЕМЕННАЯ ВЕЛИЧИНА
Величина х называется переменной,
если она принимает различные значения.
1. Последовательность x
–
переменная величина.
Пример:
xn
n
x2
x4
1
n
–
или. 1, 1 , 1 ,...
2 3
–
Областью значений переменной
называется множество всех ее
значений.
0
2. Переменная х, где
x или x D
x1
x3
1
х
2
х
х
0
х
a
D
b
х

2. Понятие функции

•Y=f(x)
Понятие функции
Аналитический
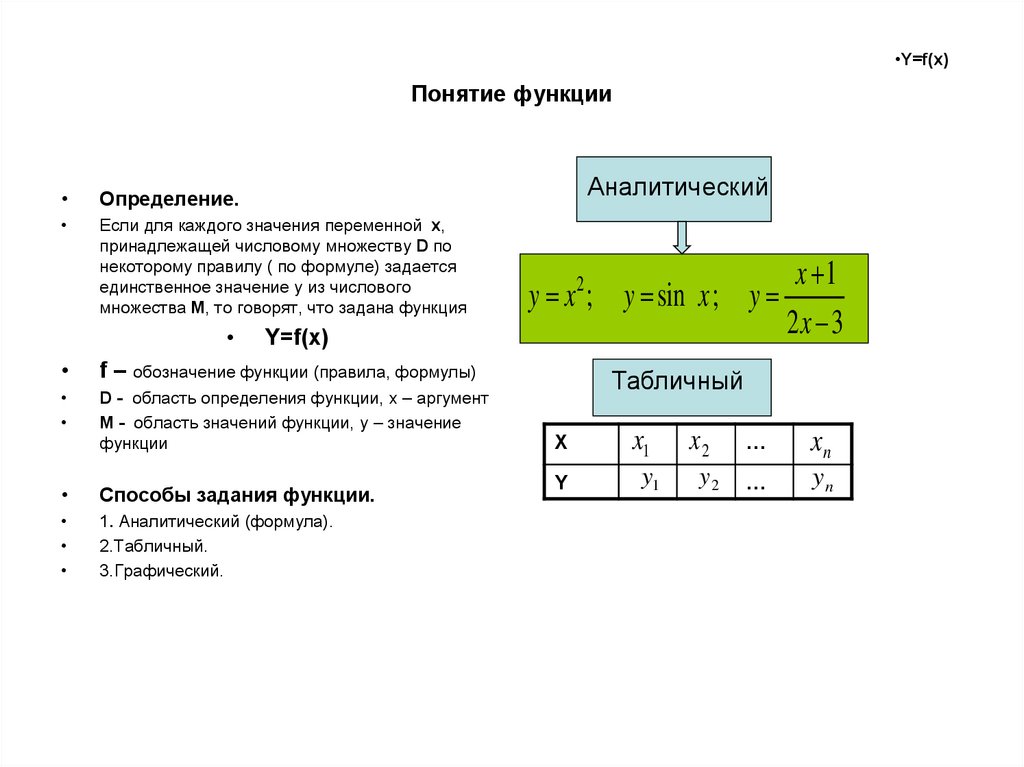
Определение.
Если для каждого значения переменной x,
принадлежащей числовому множеству D по
некоторому правилу ( по формуле) задается
единственное значение y из числового
множества М, то говорят, что задана функция
y x2 ; y sin x ; y
Y=f(x)
f – обозначение функции (правила, формулы)
D - область определения функции, х – аргумент
М - область значений функции, y – значение
функции
Способы задания функции.
1. Аналитический (формула).
2.Табличный.
3.Графический.
x 1
2x 3
Табличный
Х
Y
x1
y1
x2
y2
…
xn
…
yn

3. Графический способ задания функции

•Y=f(x)
Графический способ задания функции
Y
Определение.
Графиком функции Y=f(x) называется множество точек P(x,Y) на плоскости
XOY, абсциссами которых являются значения аргумента х, а ординатами
– соответствующие значения функции Y=f(x)
M
Y
P(x,f(x))
Примеры. 1. Линейная функция
y kx b
D
0
x
2. Квадратичная функция
X
y x2
3. Числовая последовательность
y x2
a1, a2 , , an ,
y
y
- как функция целочисленного аргумента
Y=kx+b
0
х
0
n N
an f (n)
x
1
an
1
2
1
n
1
3
0
1
2
3

4.

•Y=f(x)

5.

•Y=f(x)

6.

•Y=f(x)

7.

•Y=f(x)

8.

•Y=f(x)

9.

•Y=f(x)

10.

•Y=f(x)

11.

•Y=f(x)

12.

•Y=f(x)

13.

•Y=f(x)

14.

•Y=f(x)

15.

•Y=f(x)

16.

•Y=f(x)

17.

•Y=f(x)

18.

•Y=f(x)

19.

•Y=f(x)

20.

•Y=f(x)

21.

•Y=f(x)

22.

•Y=f(x)

23.

•Y=f(x)

24.

•Y=f(x)

25.

•Y=f(x)

26.

•Y=f(x)

27.

•Y=f(x)

28.

•Y=f(x)

29.

•Y=f(x)

30.

•Y=f(x)

31.

•Y=f(x)

32.

•Y=f(x)

33.

•Y=f(x)

34.

•Y=f(x)

35.

•Y=f(x)

36.

•Y=f(x)

37.

•Y=f(x)

38.

•Y=f(x)

39.

•Y=f(x)

40. Предел числовой последовательности

•Y=f(x)
Предел числовой последовательности
1. Последовательность
xn a (lim xn a)
Пример.
1
0
n
0
1 1
n
5
1
4
1
3
1
2
1
х

41. Определение. Число a называется пределом последовательности , если для любого положительного существует такое целое

•Y=f(x)
Определение.
Число a называется пределом последовательности хn , если для
любого положительного существует такое целое
положительное N , зависящее от , что при всех
целых значениях n больших, чем N , выполняется
неравенство x a
Логические символы
n
lim xn a
0 N N ( ) 0 :
По определению (если)
n N ( ) xn a
Любой, для любого,
Для всех
Существует, найдется
Следует,
(логическое следствие)
Равносильно, эквивалентно
(логическая равносильность)

42. Предел функции.

•Y=f(x)
Предел функции.
Пример.
lim x 2 4
x 2
-окрестность
y x2
y
Для произвольной
-окрестности
точки 4 оси OY существует -окрестность
точки 2 на оси OX такая, что при всех
значениях х из -окрестности значения
y x 2 будут принадлежать -окрестности
4
3
2
1
-окрестность
-1
0
1
2
х

43. Предел функции.

•Y=f(x)
Предел функции.
y
-окрестность
y=f(x)
Определение.
Число b называется пределом функции f(x)
при x a, если для любого
положительного существует такое
положительное , зависящее от , что
для всех х таких, что 0 x a
выполняется неравенство
f ( x) b
f(x)
lim f ( x) b 0 ( ) 0 :
b
x a
x : 0 x a f ( x) b
0
a
х
-окрестность
х
•Число b называется пределом функции f(x) при
x a , если
• для любой -окрестности точки b
• существует такая
-окрестность точки a,
• что для всех х из -окрестности
y=f(x)
• значения
будут принадлежать окрестности.

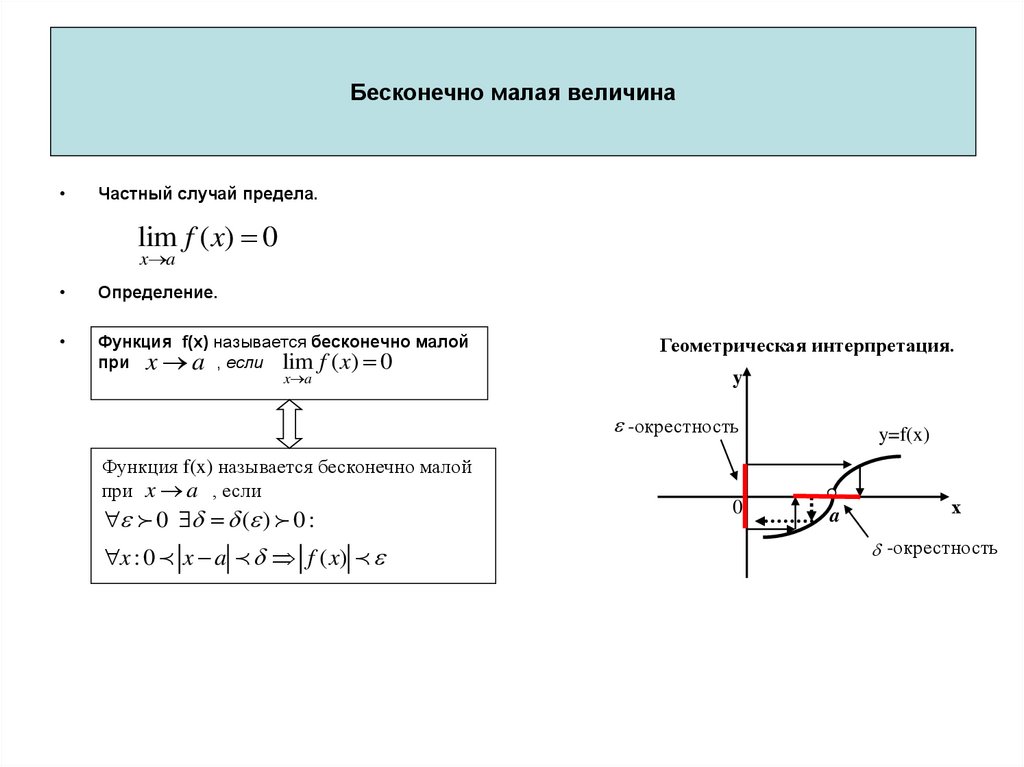
44. Бесконечно малая величина

•Y=f(x)
Бесконечно малая величина
Частный случай предела.
lim f ( x) 0
x a
Определение.
Функция f(x) называется бесконечно малой
при x a , если lim f ( x) 0
x a
Геометрическая интерпретация.
y
-окрестность
Функция f(x) называется бесконечно малой
при x a , если
0 ( ) 0 :
x : 0 x a f ( x)
0
y=f(x)
a
х
-окрестность

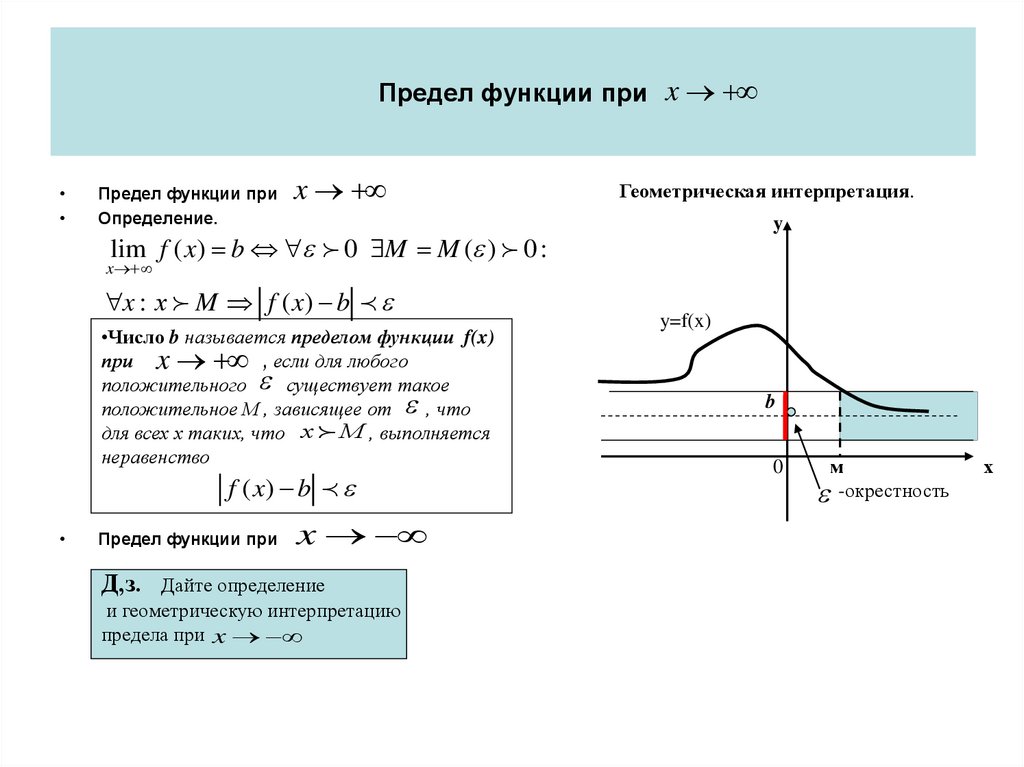
45. Предел функции при

•Y=f(x)
Предел функции при x
Предел функции при
Определение.
x
Геометрическая интерпретация.
y
lim f ( x) b 0 M M ( ) 0 :
x
x : х M f ( x) b
•Число b называется пределом функции f(x)
при x , если для любого
положительного существует такое
положительное М , зависящее от , что
для всех х таких, что х М , выполняется
неравенство
f ( x) b
Предел функции при
Д,з.
x
Дайте определение
и геометрическую интерпретацию
предела при x
y=f(x)
b
0
м
-окрестность
х

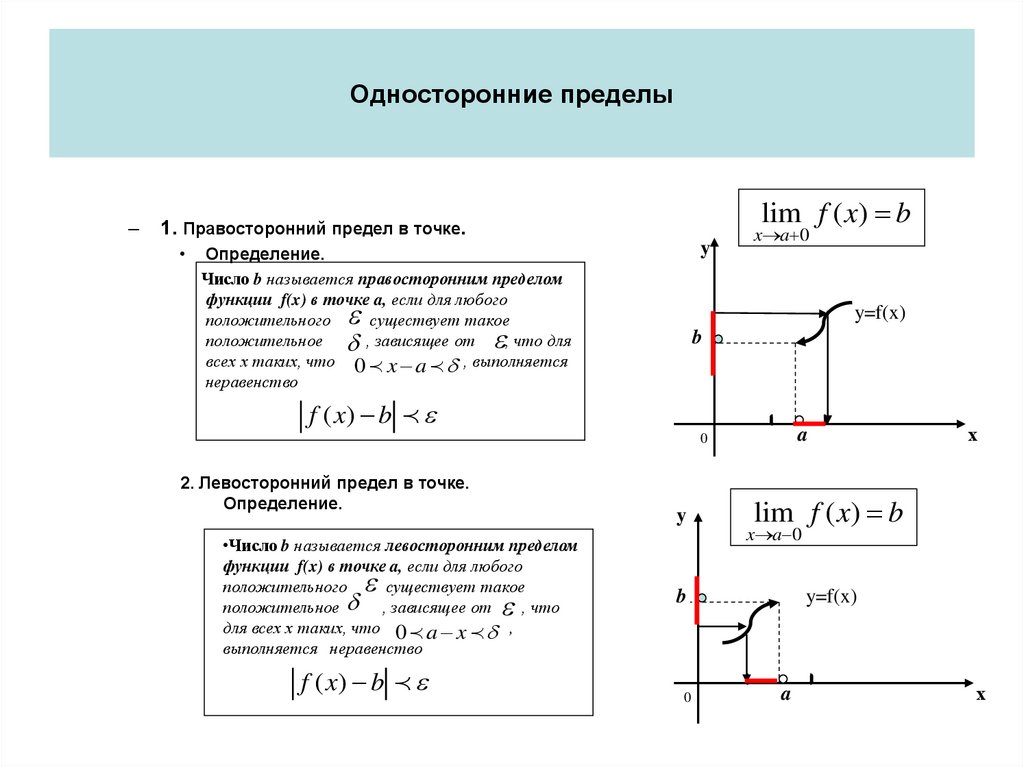
46. Односторонние пределы

•Y=f(x)
Односторонние пределы
–
lim f ( x) b
1. Правосторонний предел в точке.
y
Определение.
Число b называется правосторонним пределом
функции f(x) в точке a, если для любого
положительного
существует такое
положительное , зависящее от
, что для
всех х таких, что 0 x a , выполняется
неравенство
x a 0
y=f(x)
b
f ( x) b
a
0
2. Левосторонний предел в точке.
Определение.
y
•Число b называется левосторонним пределом
функции f(x) в точке a, если для любого
положительного
существует такое
положительное , зависящее от
, что
для всех х таких, что 0 a x ,
выполняется неравенство
f ( x) b
lim f ( x) b
x a 0
b
0
х
y=f(x)
a
х

47.

•Y=f(x)
Утверждение.
1. Если существует lim f ( x) b ,
x a
то существуют односторонние пределы
Геометрическая иллюстрация.
y
lim f ( x) b и lim f ( x) b
y=f(x)
x a 0
x a 0
( они равны между собой).
2. Если существуют оба односторонних предела
lim f ( x) b
и
x a 0
(равные между собой),
то существует
b
lim f ( x) b
x a 0
lim f ( x) b
x a
Другие обозначения односторонних пределов:
Правосторонний предел –
Левосторонний предел –
f (a 0)
f (a 0)
0
a
х