Dynamic models and the Kalman filter

1.

State Space Representation of
Dynamic Models and the
Kalman Filter
Joint Vienna Institute/ IMF ICD
Macro-econometric Forecasting and Analysis
JV16.12, L04, Vienna, Austria May 18, 2016
This training material is the property of the International Monetary Fund (IMF) and is intended
for use in IMF Institute courses. Any reuse requires the permission of the IMF Institute.
Presenter
Charis Christofides

2.

Introduction and Motivation
• The dynamics of a time series can be influenced by
“unobservable” (sometimes called “latent”) variables.
• Examples include:
Potential output or the NAIRU
A common business-cycle
The equilibrium real interest rate
Yield curve factors: “level”, “slope”, “curvature”
• Classical regression analysis is not feasible when unobservable
variables are present:
• If the variables are estimated first and then used for estimation, the
estimates are typically biased and inconsistent.

3.

Introduction and Motivation (continued)
• State space representation is a way to describe the law of
motion of these latent variables and their linkage with known
observations.
• The Kalman filter is a computational algorithm that uses
conditional means and expectations to obtain exact (from
a statistical point of view) finite sample linear predictions
of unobserved latent variables, given observed variables.
• Maximum Likelihood Estimation (MLE) and Bayesian methods
are often used to estimate such models and draw statistical
inferences.

4. Common Usage of These Techniques

• Macroeconomics, finance, time series models
• Autopilot, radar tracking
• Orbit tracking, satellite navigation (historically important)
• Speech, picture enhancement

5. Another example

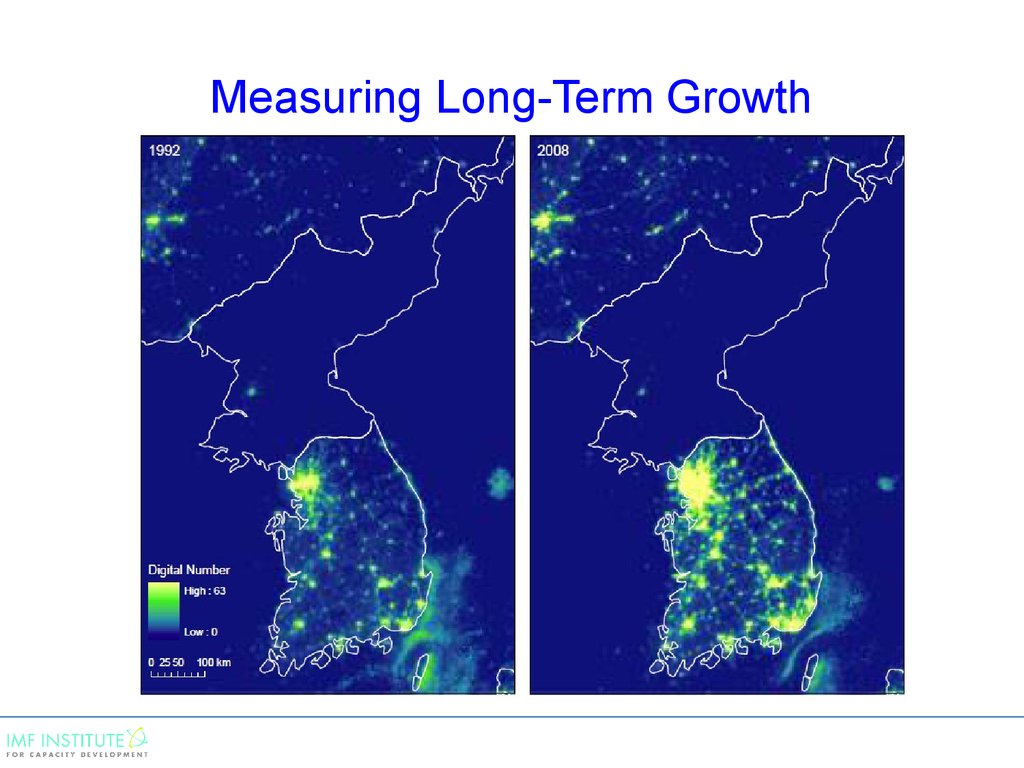
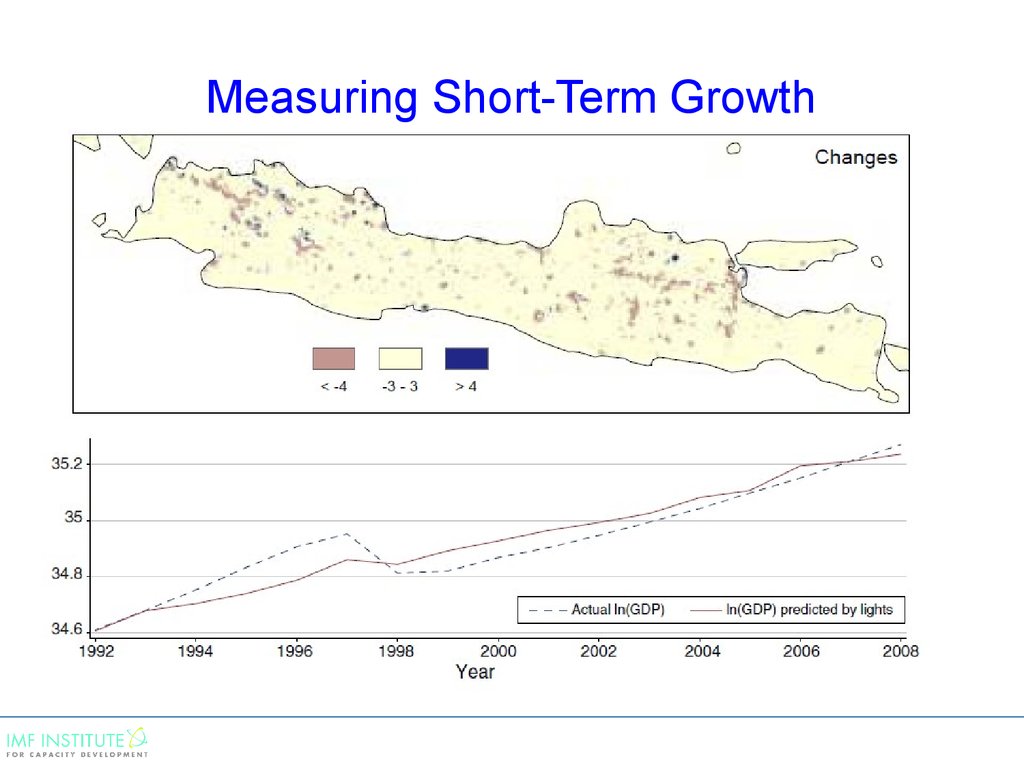
• Use nightlight data and the Kalman filter to adjust official
GDP growth statistics.
• The idea is that economic activity is closely related to
nightlight data.
• “Measuring Economic Growth from Outer Space” by
Henderson, Storeygard, and Weil AER(2012)

6. Measuring Long-Term Growth

7. Measuring Short-Term Growth

8. Measuring Short-Term Growth

9.

Content Outline: Lecture Segments
• State Space Representation
• The Kalman Filter
• Maximum Likelihood Estimation and Kalman
Smoothing

10.

Content Outline: Workshops
• Workshops
Estimation of equilibrium real interest rate, trend growth
rate, and potential output level: Laubach and Williams
(ReStat 2003);
Estimation of a term structure model of latent factors:
Diebold and Li (J. Econometrics 2006);
Estimation of output gap (various country examples).

11.

State Space Representation

12.

Basic Setup
Let yt be an (or a vector) observable variable(s) at time t.
E.g.,
• return on asset j
• nominal interest for period from t to t+j
• GDP growth
Let xt be a set of exogenous (pre-determined) variables.
E.g.,
• a constant and/or time trend
• the discount rate of the Central Bank
• demand from trading partners
Let st be one or a vector of (possibly) unobserved
variable/s: this is the so-called state variable
• Observable variables are assumed to depend on the

13.

Basic Setup
The state-space representation of the dynamics of yt is given by :
st st 1 ut
State equation
yt xt st t
Observation equation
We assume that:
• The two equations above represent the true data-generating
process for yt
• All parameters of the process are known
• Later we will relax this assumption when we discuss estimation
• The
unknown (unobserved) variables are
the last two representing error processes
st , ut , for
t
all t, with

14.

Basic Setup
The state-space representation of the dynamics of yt is given by :
st st 1 ut
State equation
yt xt st t
Observation equation
with
either a constant, or a matrix (if st is a vector)
either a constant, or a matrix (if xt is a vector)
either a constant, or a matrix (if st is a vector)
The coefficients in β are sometimes called the “loadings”.

15.

Basic Setup
The error terms in the two equations are such that:
st st 1 ut
State equation
yt xt st t
Observation equation
E[ut ] 0 and E[ t ] 0 for every t
ìΩ for every t and j t
E[ut ut j ] í
î 0 for every t and j ¹ t
ì R for every t and j t
E [ t t j ] í
î 0 for every t and j ¹ t
E[ut t j ] 0 for every t and j
ìa var-cov matrix, if ut is a vector
Ω is í
î a variance if ut is one variable
ìa var-cov matrix, if t is a vector
R is í
î a variance if t is one variable

16. Basic Setup

The error terms in the two equations are such that:
st st 1 ut
State equation
yt xt st t
Observation equation
• What if you know that uare
serially correlated:
t
, if t j
– ut ut 1 tand E[ t ] ,0 E[ t j ] ìí
î0, if t ¹ j
– Then E[ut ut 1 ] ¹ 0so one of the
assumptions is violated!
– What to do? Can you still apply the model?

17.

The State Space Representation: Examples
Example #1: simple version of the CAPM
st
yt
Φ, α, and β
Ω and R
one variable, return on all invested wealth
one variable, return on an asset
constants
constants
st st 1 ut
State equation
yt st t
Observation equation

18.

The State Space Representation: Examples
Example #2: growth and real business cycle (small open
economy with a large export sector)
• st
• Yt
sales
• xt
partner
• Φ, and Ω
s•t α, and
st β1 ut
• R
one variable, business cycle
vector, GDP growth, unemployment, retail
one variable, demand growth of trading
constants
vectors
matrix
y1,t 1,t
1,t
1,t
y2,t 2,t xt 2,t st 2,t
y
3, t 3, t
3 ,t
3, t
State equation
Observation equation

19.

The State Space Representation: Examples
Example #3: interest rates on zero-coupon bonds of different
maturity
st
yt
xt
Φ, and Ω
α and β
R
one variable, latent variable
a vector with interest rates for diff. mat.
one variable, the Central Bank discount rate
constants
vectors of constants
matrix
st st 1 ut
y
1,t 1,t
1,t
1,t
y x s
2,t 2,t t 2,t t 2,t
y
n ,t n ,t
n ,t
n ,t
State equation
Observation
equation

20.

The State Space Representation: Examples
Example #4: an AR(2) process
zt 1 zt 1 2 zt 2 vt , vt ~ N (0, v2 )
• Can we still apply the state space representation?
• Yes!
• Consider the following state equation:
zt 1 2 zt 1 1
z 1 0 z 0 vt
t 1 t 2
st
st 1
• And the observation equation:
zt 1 0 s t
yt
ut

21.

The State Space Representation: Examples
Example #4: an AR(2) process
zt 1 zt 1 2 zt 2 vt , vt ~ N (0, v2 )
• The state equation:
zt 1 2 zt 1 1
z 1 0 z 0 vt
t 1 t 2
st
st 1
• And the observation equation:
ut
z 1 0 s
t t
yt
• What are matrices Ω (var-cov of ut) and R (var-cov of t) in this
case?

22.

The State Space Representation Is Not Unique!
Consider the same AR(2) process
zt 1 zt 1 2 zt 2 vt , vt ~ N (0, v2 )
• Another possible state equation:
zt 1 1 zt 1 1
z 0 z 0 vt
t 1
2 2 t 2
2
st
st 1
ut
• And the corresponding observation equation:
z 1 0 s
t t
yt
• These two state space representations are equivalent!
• This example can be extended to AR(p) case

23.

The State Space Representation: Examples
Example #5: an MA(2) process
zt vt vt 1 , vt ~ N (0, v2 )
• Consider the following state equation:
vt 0
v 1
t 1
st
• And the observation equation:
0 vt 1 1
vt
0 vt 2 0
st 1
ut
z 1 s
t t
yt
• What are matrices Ω (var-cov of ut) and R (var-cov of t) in this
case?

24.

The State Space Representation: Examples
Example #5: an MA(2) process
zt vt vt 1 , vt ~ N (0, v2 )
• Consider the following state equation:
yt 0
v 0
t
st
1 yt 1 1
vt
0 vt 1
• And the observation equation:
st 1
ut
z 1 0 s
t t
yt
• What are matrices Ω (var-cov of ut) and R (var-cov of t) in this
case?

25.

The State Space Representation: Examples
Example #6: A random walk plus drift process
zt zt 1 vt , vt ~ N (0, v2 )
• State equation? Observation equation?
• What are the loadings ?
• What are matrices Ω (var-cov of ut ) and R (var-cov of )
tfor your state-space representation?

26.

The State Space Representation:
System Stability
• In this course we will deal only with stable systems:
• Such systems that for any initial state s0 , the state variable
(vector) st converges to a unique s (the steady state)
• The necessary and sufficient condition for the state space
representation to be stable is that all eigenvalues of are less
than 1 in absolute value:
| i ( ) | 1 for all i
• Think of a simple univariate AR(1) process ( zt 1 zt 1 vt )
• It is stable as long as | 1 | 1
• Why? So that it is possible to be right at least in the “long-run”.

27.

The Kalman Filter

28. Kalman Filter: Introduction

• State Space Representation [univariate case]:
st st 1 ut
ut ~ i.i.d . N (0, )
2
u
yt xt st t t ~ i.i.d . N (0, )
2
( , , , u2 , 2 )
are known
• Notation:
– st|t 1 E ( st | y1 ,..., yt 1 ) is the best linear predictor of st
conditional on the information up to t-1.
– yt |t 1 E ( yt | y1 ,..., yt 1 ) is the best linear predictor of yt
conditional on the information up to t-1.
– st |t E ( st | y1 ,..., yt ) is the best linear predictor of st
conditional on the information up to t.

29. Kalman Filter: Main Idea Moving from t-1 to t

• Suppose we know st |t 1 and yt |t 1 at time t-1.
• When arrive in period t we observe yt and xt
• Need to obtain st|t !
• If we know st|t ,
– using the state equation: st 1|t st|t
– using the observation equation: yt+1|t = xt+1 + st+1|t
• The key question: how to obtain st|t from yt ?
Why?

30. Kalman Filter: Main Idea How to update st|t ?

• Idea: use the observed prediction error
st |t
t,
yt ytot |t infer
the state at time
1
• It turns out it is optimal to update it using
st|t st |t 1 K t ( yt yt|t 1 )
• K t is called Kalman gain
– It measures how informative is the prediction error about the
underlying state vector
• How do you think it depends on the variance of the observation error?
– It is chosen so that the new prediction error is orthogonal to all of the
previous ones.
• Thus there is no (linear) predictable component in generated errors.

31. Kalman Filter: More Notations

Pt|t 1 E (( st st|t 1 ) 2 | y1 ,..., yt 1 )is the prediction error variance
of s given the history of observed variables up to t-1.
t
2
F
E
((
y
y
)
| y1 ,..., yt 1 )is the prediction error variance
t |t 1
t
t |t 1
of yt conditional on the information up to t-1.
2
P
E
((
s
s
)
| y1 ,..., yt ) is the prediction error variance of
t |t
t
t |t
st
conditional
on the information up to t.
• Intuitively the Kalman gain is chosen so that Pt|t is minimized.
– Will show this later.

32. Kalman Gain: Intuition

• Kalman gain is chosen so that Pt |t is minimized.
• It can be shown that
K t Pt|t 1 ( 2 Pt|t 1 R) 1
• Intuition:
– If a big mistake is made forecasting s
(
is large), put
t |t 1 Pt |t 1
a lot weight on the new observation (K is large).
– If the new information is noisy (R is large), put less weight
on the new information (K is small).

33. Kalman Filter: Example

K t Pt|t 1 ( 2 Pt|t 1 R) 1
• Kalman gain is
• Consider
2
s
u
,
u
~
N
(
0
,
t
t
t
u)
– State equation
– Observation equation yt st t , t ~ N (0, 2 )
– Additionally 2 2, where is a constant
u
• Assume that we picked P1|0 u (we don’t know anything
about s1 ).
• Can you calculate the Kalman gain in the 1 st period,K1?
• What is the interpretation?
2

34. Kalman Filter: The last step

• How do we get from Pt |t 1 to Pt 1|t using yt ?
• Recall that for a bivariate normal distribution
1 12 12
z1
z 2 | z1 ~ N ( 2 12 ( 12 ) 1 ( z1 1 ), 22 12 ( 12 ) 1 12 )
~ N ,
2
2
z2
12
2
• Using this property and the fact that E[ st|t 1 | yt ] st|t
yt |t 1 Ft |t 1
yt
,
| ( y1 , , yt 1 ) ~ N
st|t 1 Pt|t 1
s
t
Pt|t 1
Pt|t 1
E ( st st|t 1 )( yt yt|t 1 ) | y1 , yt 1 E ( st st|t 1 )( ( st st|t 1 ) t ) | y1 , yt 1 Pt|t 1
• Thus, st|t = st|t-1+ Pt|t-1(Ft|t-1)-1(yt - yt|t-1) and
Pt|t = Pt|t-1 – Pt|t-1(Ft|t-1)-1 Pt|t-1
Kalman gain

35. Kalman Filter: Finally

• From the previous slide
st|t = st|t-1+ Pt|t-1(Ft|t-1)-1(yt - yt|t-1)
Pt|t = Pt|t-1 – Pt|t-1(Ft|t-1)-1 Pt|t-1
• Need: from Pt |t 1 to Pt 1|t using yt
Ft |t 1 E ( yt yt|t 1 ) 2 | y1 , yt 1 E ( ( st st |t 1 ) t ) 2 | y1 , yt 1 2 Pt |t 1 R
• Thus, we get the expression for the Kalman gain:
• Similarly
K t Pt|t 1 ( 2 Pt|t 1 R) 1
Pt 1|t E ( st 1 st 1|t ) 2 | y1 , , yt E ( ( st st|t ) ut ) 2 | y1 , yt 2 Pt |t
• And we are done!

36. Kalman Filter: Review

• We start from st|t 1 and Pt |t 1 .
yt|t-1 = xt + st|t-1
Ft|t 1 2 Pt|t 1 R
• Calculate Kalman gain
K t Pt|t 1 ( 2 Pt|t 1 R) 1
• Update using observed yt
st |t st|t 1 K t ( yt yt|t 1 )
Pt|t = Pt|t-1 – Pt|t-1(Ft|t-1)-1 Pt|t-1
• Construct forecasts for the next period
st 1|t st|t
• Repeat!
Pt 1|t 2 Pt|t

37. Kalman Filter: How to choose initial state

• If the sample size is large, the choice of the initial state is not
very important
• In short samples can have significant effect
• For stationary models
s1|0 s *
P1|0 P *
• Where
s* s*
P * P *
• Solution to the last equation is P * [ I ] 1 vec( )
• Why? Under some very general conditions
P P * as t
t |t 1

38. Kalman Filter as a Recursive Regression

• Consider a regular regression function
E[ s | y ] a by
where
a E[ s ] b E[ y ]
• Substituting
b Cov ( s, y ) (Var ( y )) 1
E[ s | y ] E[ s ] Cov ( s, y ) Var ( y ) 1 [ y E[ y ]]
• From one of the previous slides:
st|t = st|t-1+ Pt|t-1(Ft|t-1)-1(yt - yt|t-1)

39. Kalman Filter as a Recursive Regression

• Consider a regular regression function
E[ s | y ] a by
where
a E[ s ] b E[ y ]
b Cov ( s, y ) (Var ( y )) 1
• Substituting
E[ s | y ] E[ s ] Cov ( s, y ) Var ( y ) 1 [ y E[ y ]]
• From one of the previous slides
st|t = st|t-1+ Pt|t-1(Ft|t-1)-1(yt - yt|t-1)
Because
Cov ( st , yt | y1 , yt 1 ) Pt|t 1
Var ( yt | y1 ,..., yt 1 ) Ft|t 1
st|t 1 E ( st | y1 ,..., yt 1 )
yt|t 1 E ( yt | y1 ,..., yt 1 ) st|t E[ E ( st | y1 ,..., yt 1 ) | yt ]

40. Kalman Filter as a Recursive Regression

• Thus the Kalman filter can be interpreted as a recursive
regression of a type
t
st y vt
1
t
where vt st y is the forecasting error at time t
1
• The Kalman filter describes how to recursively estimate
t and thus obtain st |t E[ st | y1 ,... yt ]

41. Optimality of the Kalman Filter

• Using the property of OLS estimates that constructed residuals
are uncorrelated with regressors
E[vt ] 0 E[vt yt ] 0 for all t
• Using the expression for
t
vt st y
1
and the state equation, it is easy to show that
for
E[vallyt and
] k=0..t-1
0
t
t k
• Thus the errors vt do not have any (linear) predictable
component!

42. Kalman Filter Some comments

Within the class of linear (in observables) predictors the Kalman filter
algorithm minimizes the mean squared prediction error (i.e., predictions
of the state variables based on the Kalman filter are best linear unbiased):
Min E[ s t ( st |t 1 K t ( yt yt |t 1 )) ]
2
Kt
Pt |t 1
Kt 2
Pt |t 1 R
If the model disturbances are normally distributed, predictions based on
the Kalman filter are optimal (its MSE is minimal) among all predictors:
E[ s t ( st|t 1 K t ( yt yt|t 1 )) ] Min E[ s t f ( y1 ,..., yt ) ]
2
2
f ( y1 ,..., yt )
In this sense, the Kalman filter delivers optimal predictions.

43.

Kalman Filter - Multivariate Case
• The Kalman Filter algorithm can be easily generalized to the
generic multivariate state space representation, including
exogenous variables:
s t+1 =Φs t + u t+1 , E u tu 't Ω
y t = Axt +Βs t + ε t , E ε tε 't R
• Defining similarly as before:
s t|t-1 = E s t | y1 ,…, y t-1 , Pt|t-1
y t|t-1
'
E st st|t-1 st st|t-1 | y1 ,…, y t-1
'
= E y t | y1 ,…, y t-1 , Ft E y t - y t|t-1 y t - y t|t-1 | y 1 ,…, y t-1
• Now we have vectors and matrices

44. Kalman Filter Algorithm – Multivariate Case

Initialization: s1|0 , P1|0
1: y t|t-1 = Axt + Bs t|t-1
2 : Ft = BPt|t-1B' + R
3 : K t = Pt|t-1B' (Ft )-1
4 : s t|t = s t|t + K(y t - y t|t-1 )
5 : Pt|t = Pt|t-1 - Pt|t-1B' (Ft )-1 BPt|t-1
6 : s t+1|t =Φs t|t
7 : Pt+1|t =ΦP t|tΦ ' + Ω
Repeat 1,...,7 from t 1 to t T

45. Kalman Filter Algorithm – Multivariate Case (cont.)

How do we obtain these expressions?
y t|t-1 = E Axt + Bs t +ε t |y 1,…, y t-1 Ax t + Bs t|t-1
Ft = E (y t y t|t-1 )(y t y t|t-1 )' | y 1 ,…, y t-1
'
E ( B (s t sεt|t-1 ) st )( Bs ( t εt|t-1 ) y ,…,
t ) | y1
BP
R
t-1 B +
t|t-1
'
Also:
E (y t y t|t-1 )(s t - s t|t-1 )' | y 1 ,…, y t-1 E (B(s t sεt|t-1 )s ts)( t yt|t-1,…,
)' | y1
BPt|t-1
Thus:
y t|t-1 Ft
BPt|t-1
yt
,
| y 1 ,…, y t-1 ~ N
(BPt|t-1 ) ' Pt|t-1
st
s t|t-1
t-1

46. Kalman Filter Algorithm – Multivariate Case (cont.)

How we obtained these expression? (cont.)
y t|t-1 Ft
BPt|t-1
yt
,
| y 1 ,…, y t-1 ~ N
P
B'
P
t|t-1
st
s t|t-1 t|t-1
Using the property for a multivariate normal distribution to get
conditional disttribution:
s t|t ~ N s t|t-1 + Pt|t-1B'(Ft )-1 y t - y t|t-1 + , Pt|t-1 Pt|t-1B'(Ft )-1 BPt|t-1
1 42 43
1 4 4 44 2 4 4 4 43
Kt
Pt|t
1
4
4
4
4
4
2
4
4
4
4
43
st|t
Also:
sΦs
+E
u
t+1|t
yt ,…,
t+1y|
1
PΦ
) s
t+1|t s Es ( +( ut t|tΦ
Φs
t
t+1s)( ( t
t|t
'
)
+
u
)
t|t
t+1 | y 1 ,…, yΦP
t Φ
'
Ω
t|t

47.

ML Estimation and Kalman Smoothing

48.

Maximum Likelihood Estimation
• The algorithm in the previous section assumes knowledge of
the parameters. If these are not known, estimates are needed.
• Consider the univariate case:
st 1 st ut 1 , E ut2 u2
yt xt st t , E t2 2
and using that st is normally distributed (ut is normal) then
( yt | y1 ,..., yt 1 ) ~ N ( yt |t 1 , Ft|t 1 )
• Thus we can do maximum likelihood estimation
1
1
1
2
log l ( , , , u , ) log 2 log | Ft|t 1 |
( yt yt|t 1 )
2
2 Ft |t 1
t 1
2
T
• Similarly with the multivariate case:
(y t | x t , y 1 ,…, y t-1 ) ~ N (y t|t-1 , Ft )

49.

Maximum Likelihood Estimation
To estimate model parameters through maximizing loglikelihood:
Step 1: For every set of the underlying parameters, θ
Step 2: run the Kalman filter to obtain estimates for the
sequence
yt|t 1 , Ft|t 1
Step 3: Construct the likelihood function as a function of θ
Step 4: Maximize with respect to the parameters.

50.

Kalman Smoothing
• For each period t, the Kalman filter uses only information
available up to time t:
E[s t | y 1 ,…, y t-1 ] s t|t-1
• Is it possible to use all the information available so as to obtain
an even better estimate of st: E[st | y 1 ,…, y T ] ?
• This is called smoothed inference of the state and denoted by
s t|T
• In general, we can obtain the smoothed inference
s t|τ , > t

51.

Kalman Smoothing
Using the same principles for normal conditional distribution, it is
possible to show that there is a recursive algorithm to compute
s t|Tstarting from
s T|T
:
Step 1: use Kalman filter to estimate s1|1 , …, sT|T
Step 2: use recursive method to obtain, s t|T , the smoothed
estimate of st:
s t|T = s t|t + J t (s t+1|T - s t+1|t )
where
'
J t = PΦ
P(
t|t
1
)
t+1|t

52.

Conclusion
• Many models require estimations of unobserved variables,
either because these are of economic interest, or because one
needs them to estimate the model parameters (example,
ARMA).
• The Kalman filter is a recursive algorithm that:
• provides efficient estimates of unobserved variables, and
their MSE;
• can be used for forecasting given estimates of MSE;
• is used to initialize maximum likelihood estimation of models
(for example, of ARMA models) by first producing good
estimates of un-observed variables;
• can also be used to smooth series for unobserved variables.