Similar presentations:
Quantum computers, quantum computations
1. Quantum computers, quantum computations
H. GomonayNational Technical University of Ukraine
JGU, Mainz, Germany
2. Take-home message
The quest for a quantum computer reminds meof the endless quests for WIMPs, strings,
sparticles, magnetic monopoles, etc. Succeed
they or not, they bring to development of new
knowledges and technologies, push the most
talented people into science and keep fun from
research. Same as it ever was.
3. Motivation
Moore’s lawMeters
Nanometers
40 years
Electronic lamp
Microprocessor 80486dx2
4. Outline
HistoryPrinciples of quantum computation
Di Vincenzo criteria
Superconducting qubit
Some algorithms
Architecture
Challenges and problems
5. History in facts
1935 – A. Einstein doubts in adequacy ofquantum mechanics & introduces entangled
states
1982 – R. Feynman predicts
possibility of quantum computations
2007 – D-Wave Systems presents
16 qubit quantum processor
Orion
6.
2012 – S. Haroche & D. J. Wineland winnNobel prize for for ground-breaking
experimental
methods
that
enable
measuring and manipulation of individual
quantum systems"
2015 – Google tests the D-Wave
2X quantum annealer, ~1000 qb
7. History in diagrams
Classical vs quantum:speed up
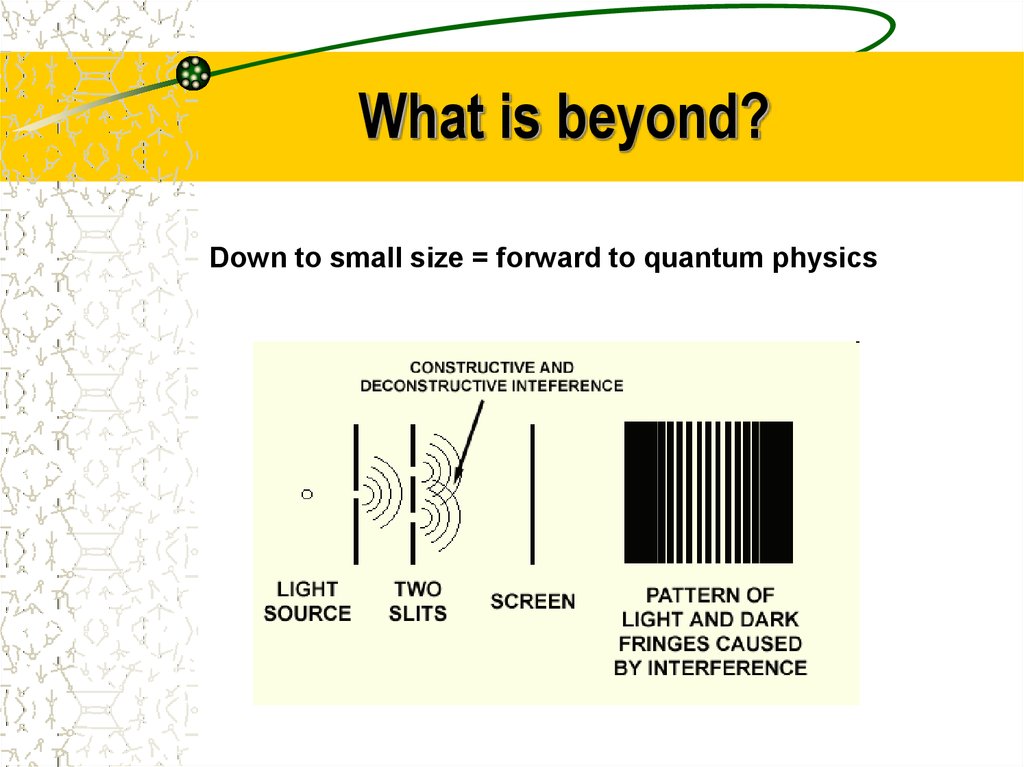
8. What is beyond?
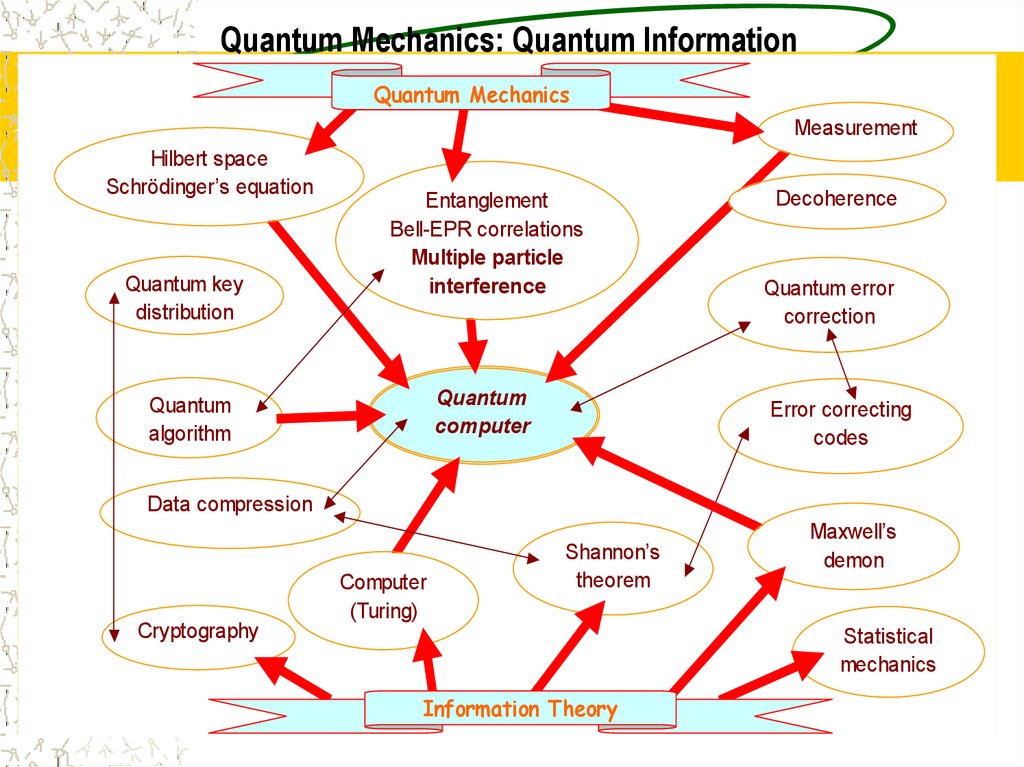
Down to small size = forward to quantum physics9. Quantum Mechanics: Quantum Information
Quantum MechanicsMeasurement
Hilbert space
Schrödinger’s equation
Quantum key
distribution
Entanglement
Bell-EPR correlations
Multiple particle
interference
Quantum
computer
Quantum
algorithm
Decoherence
Quantum error
correction
Error correcting
codes
Data compression
Cryptography
Computer
(Turing)
Shannon’s
theorem
Maxwell’s
demon
Statistical
mechanics
Information Theory
10. What is all about or new applications of quantum physics
“Hacking” cryptoKeeping secrets
Data search speed up
Bioinformatics
Outer space opening
Fundamental
problems
Factorization of 256-digit
number:
Classic – 2N 1070 years
Quantum – N2 ~ 10 seconds
11. What is QC?
D-WaveQC is the physical device that utilizes
quantum properties for information
processing
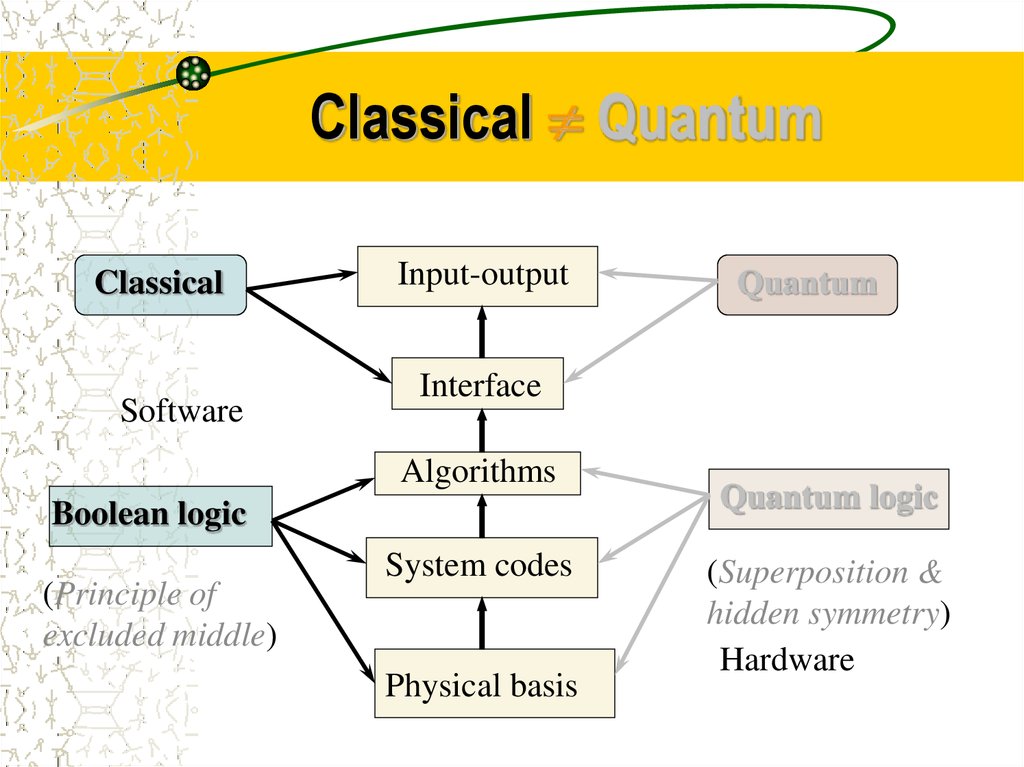
12. Classical Quantum
Classical QuantumClassical
Software
Input-output
Interface
Algorithms
Boolean logic
(Principle of
excluded middle)
Quantum
System codes
Physical basis
Quantum logic
(Superposition &
hidden symmetry)
Hardware
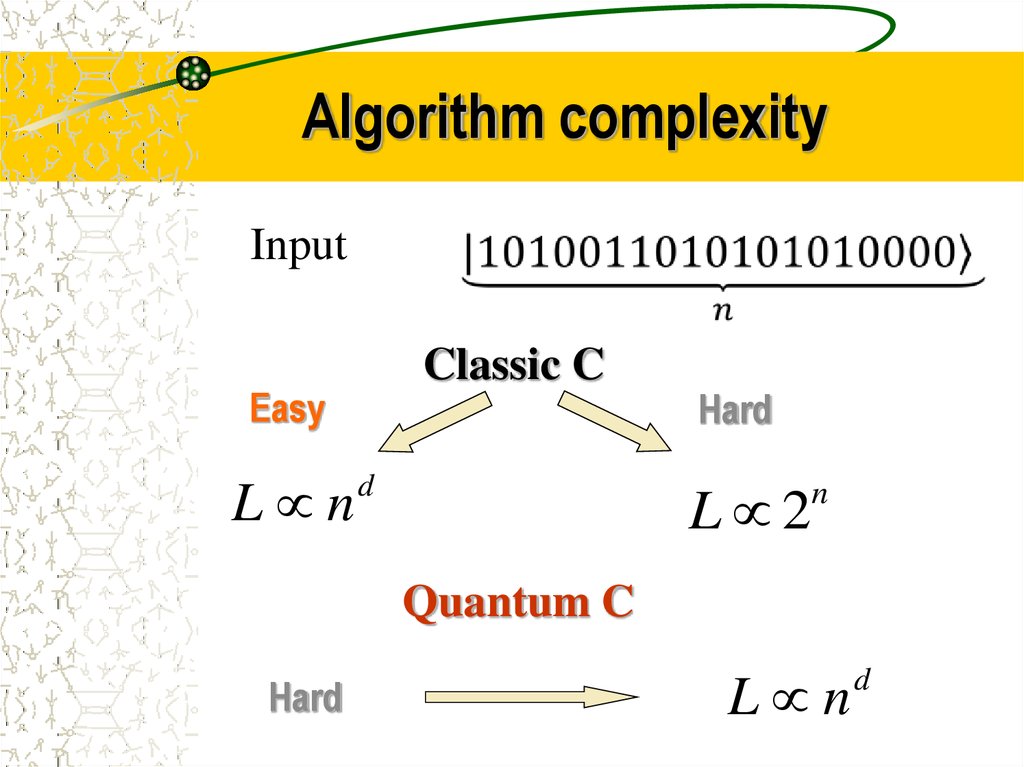
13. Algorithm complexity
InputClassic C
Easy
L n
Hard
L 2
d
n
Quantum C
Hard
L n
d
14. Qubit = Quantum bit
icos 0 e sin 1
1
1
0
Bit
0 1
0
Qubit
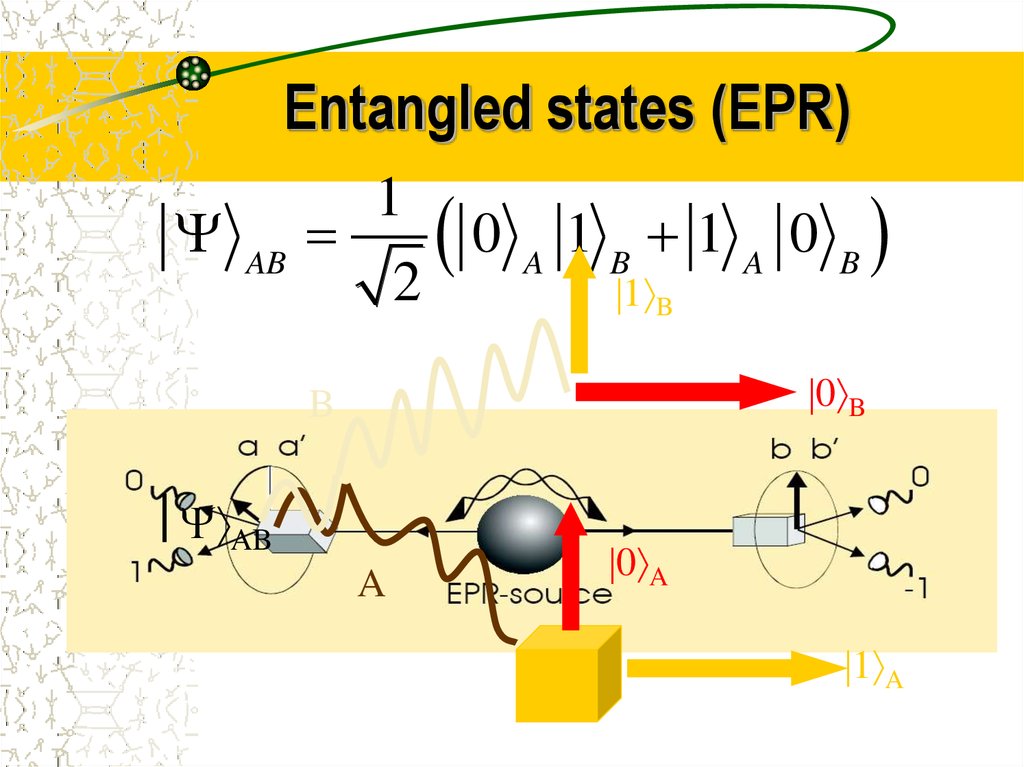
15. Entangled states (EPR)
AB1
0
2
A
1B 1
1 B
A
0
B
0 B
B
AB
A
0 A
1 A
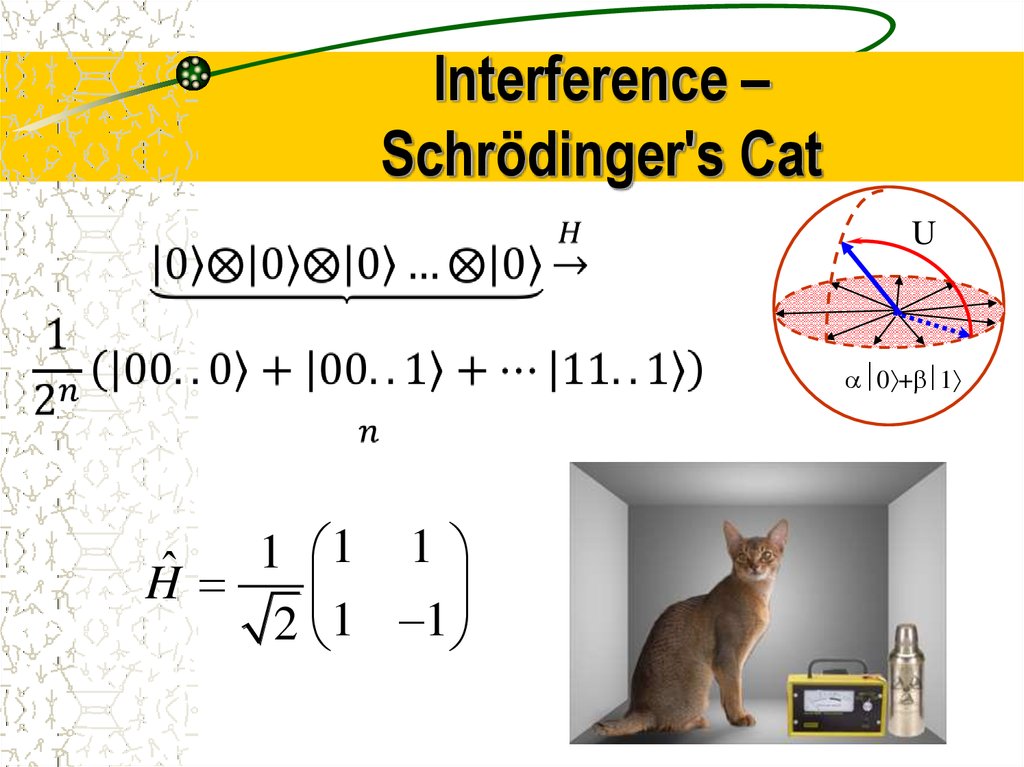
16. Interference – Schrödinger's Cat
U0 + 1
1
1
1
ˆ
H
1 1
2
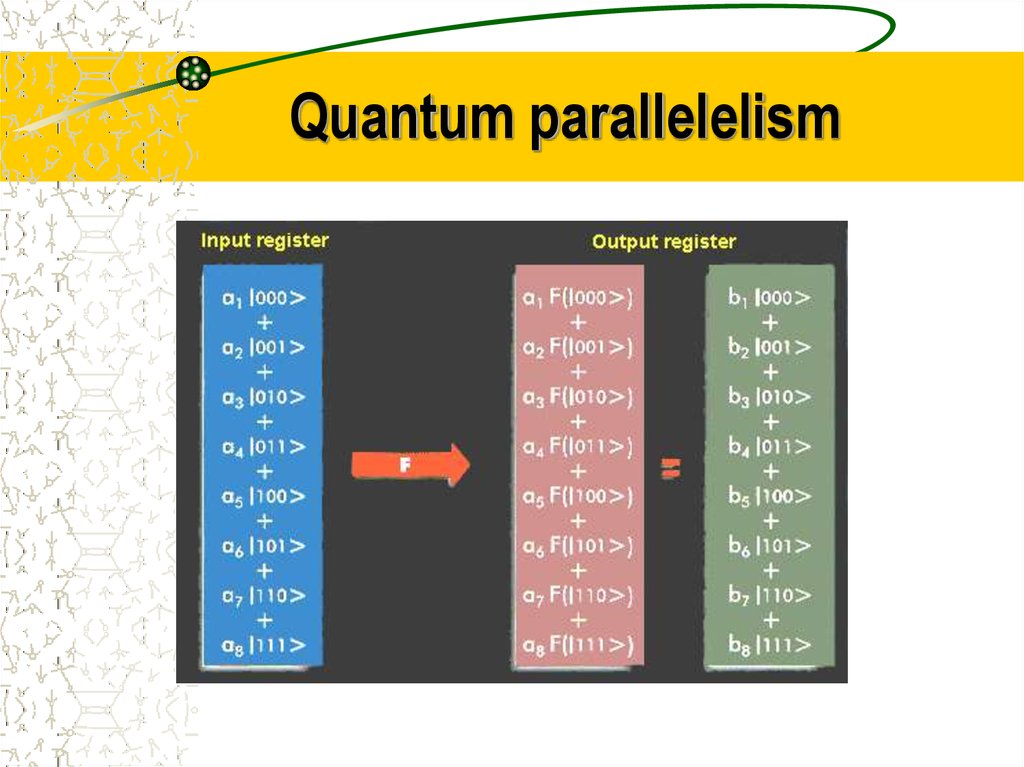
17. Quantum parallelelism
18. Parallel quantum algorithm
ina 0 1 b 1 0
out
a f (01) b f (10)
f
2n 1
c
x 0
2n 1
x
cx f ( x )
f
x
x 0
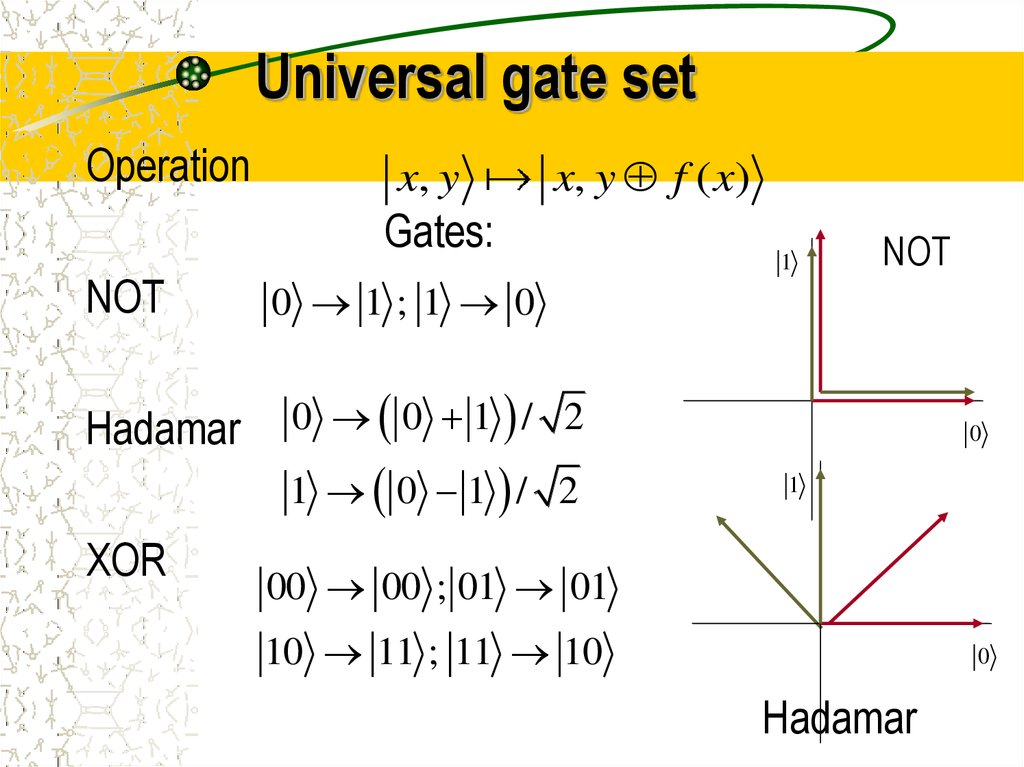
19. Universal gate set
Operationx, y
x, y f ( x)
Gates:
NOT
Hadamar
XOR
1
NOT
0 1;1 0
0 0 1 / 2
1 0 1 / 2
0
1
00 00 ; 01 01
10 11 ; 11 10
0
Hadamar
20. Principles of quantum computation
Computation: unitary evolutionn
Hˆ Bzi (t ) ˆ zi Bxi (t ) ˆ xi J ij (t ) ˆ i ˆ j
i 1
i j
i ˆ
out exp H (t )dt in
Readout: measurement
Pˆ out 0 0 1 ... 1
Avoiding decoherence
21. Di Vincenzo criteria
Selectivity (addressing each qubit)High sensitivity = Good control
Large decoherence time
( decoh/ gate >104)
Readout Measurability
Scalability (>100 qubits)
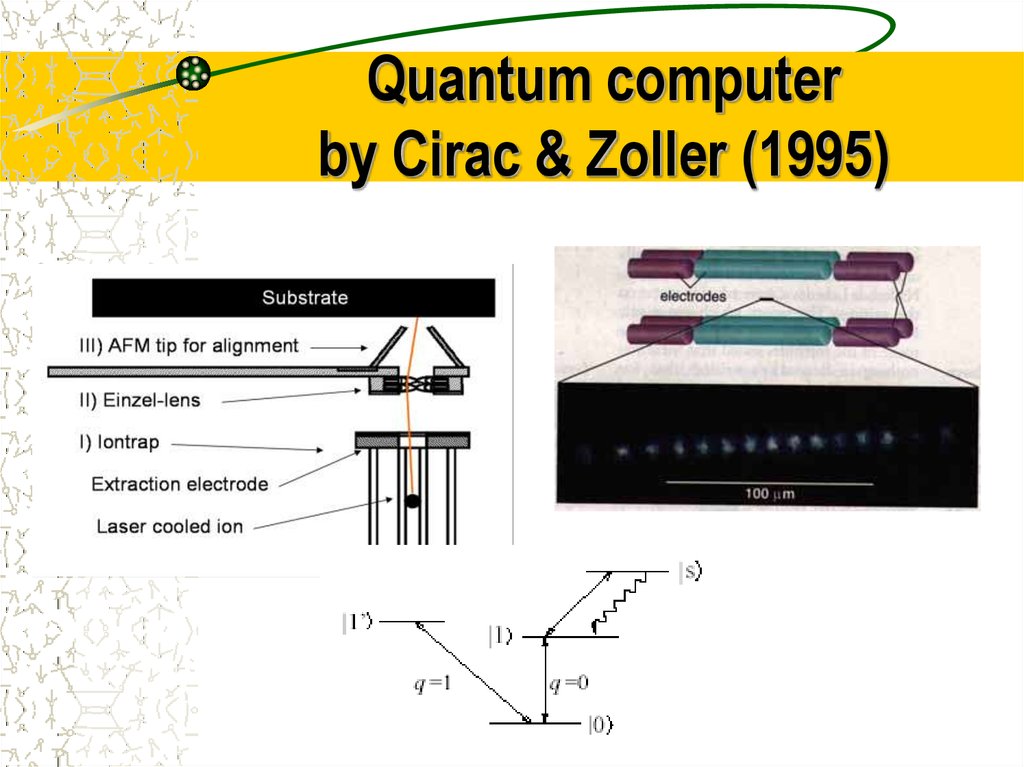
22. Quantum computer by Cirac & Zoller (1995)
Quantum computerby Cirac & Zoller (1995)
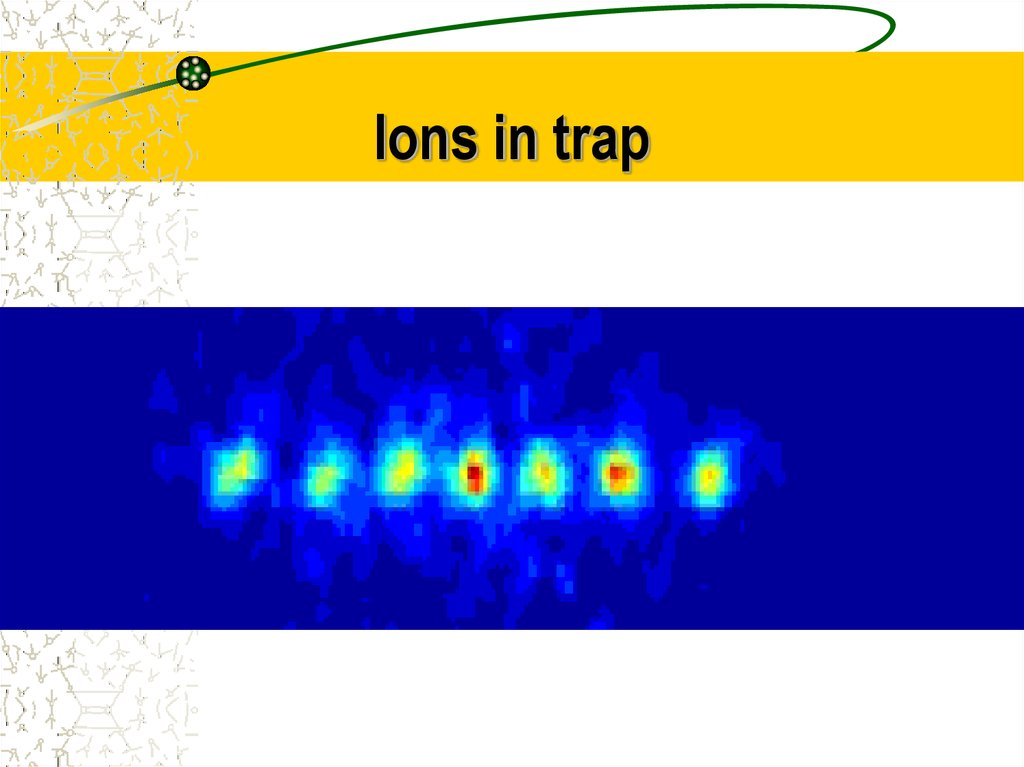
23. Ions in trap
24. Qubit: micro or macro?
Measurement duration:t ~ op ~ R1 ~ 10 9 s
Limitations:
E t
Energy splitting:
E B B
Qubit = 1 electron spin:
B ~ 10 23 J/T
-3 – 10-7
2
k~10
Measured
E E k
2
19
E
/
k
~
10
J
R
Min splitting
B E / B ~10 4 T
Min field
Impossible! We need macrospin!
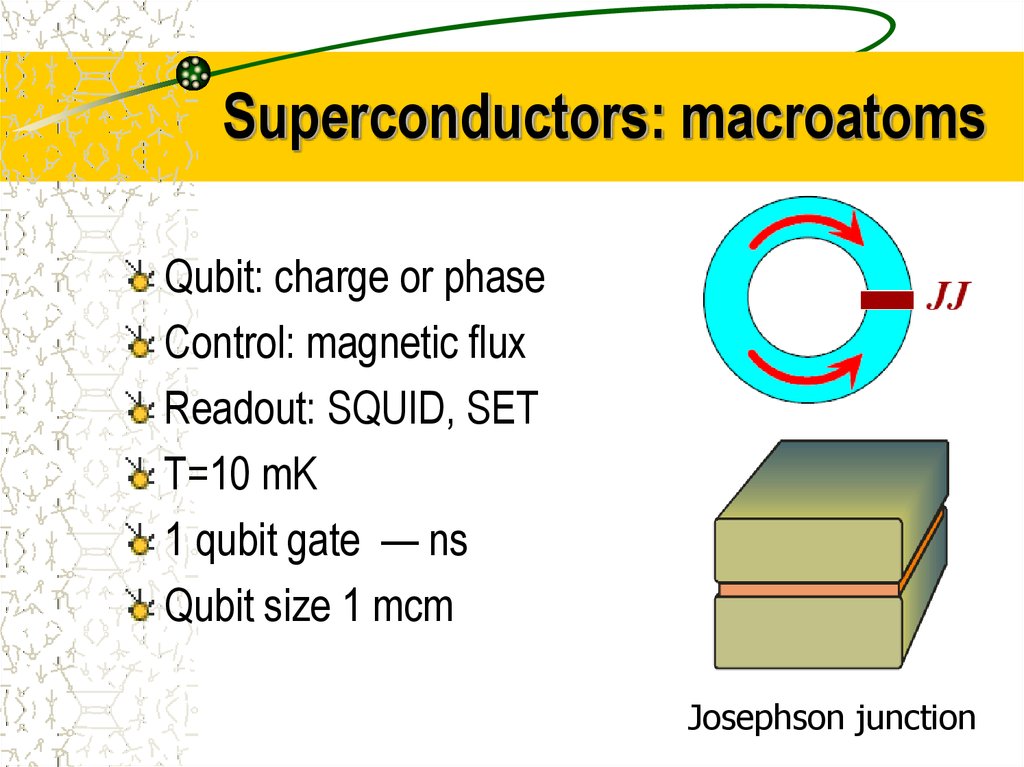
25. Superconductors: macroatoms
Qubit: charge or phaseControl: magnetic flux
Readout: SQUID, SET
T=10 mK
1 qubit gate — ns
Qubit size 1 mcm
Josephson junction
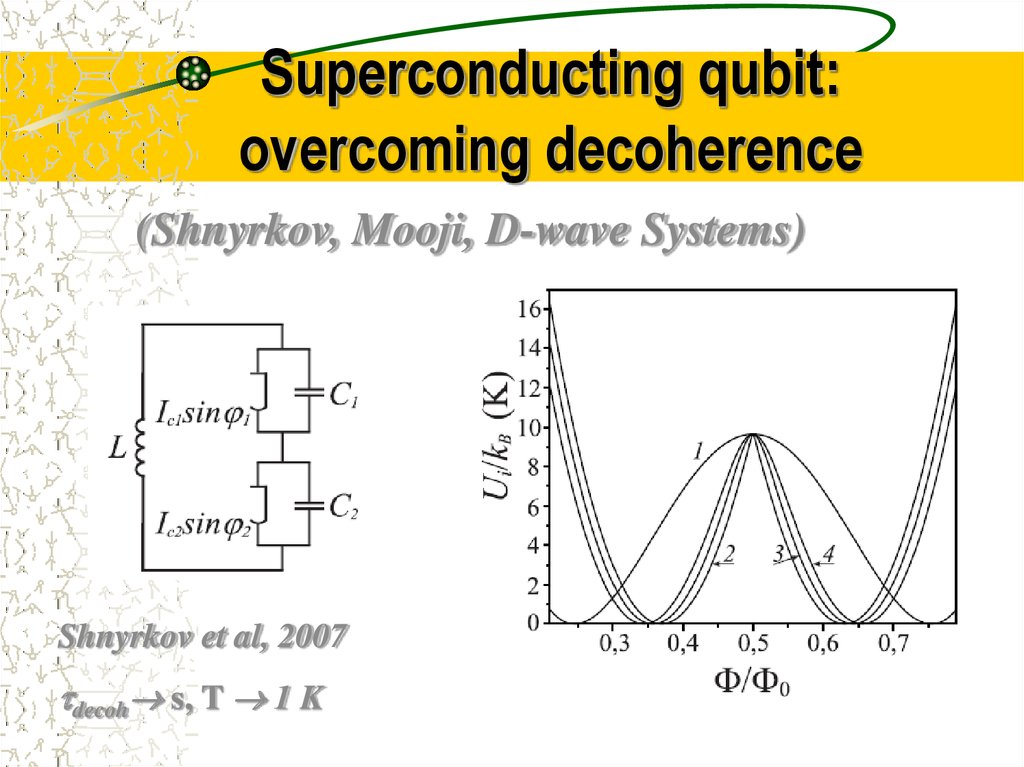
26. Superconducting qubit: overcoming decoherence
(Shnyrkov, Mooji, D-wave Systems)Shnyrkov et al, 2007
decoh s, T 1 K
27. Flux qubit: theory
250e= ...
U ( , e ), a.u.
200
0
150
3/4 0
1/2 0
100
1/4 0
50
0
0
-2
~ 10 10 B
8
U SIS ( , e )
10
-1
0
/ 0
( e )
2L
2
I ct (0) 0
2
cos 2
0
1
2
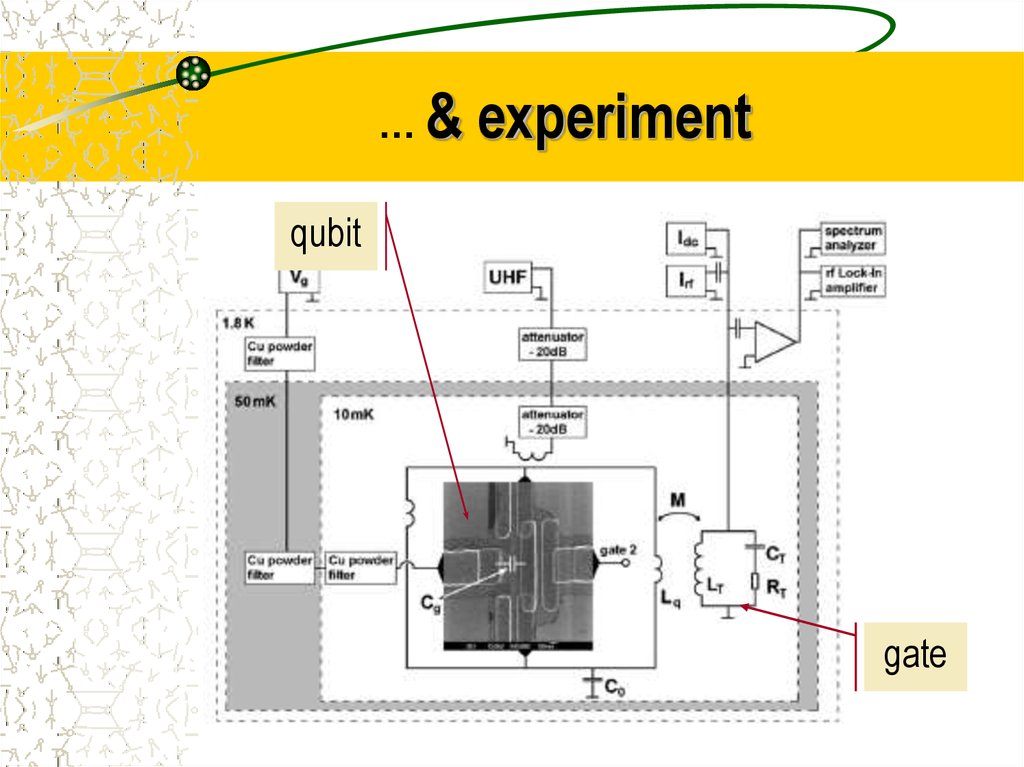
28. … & experiment
…&experiment
qubit
gate
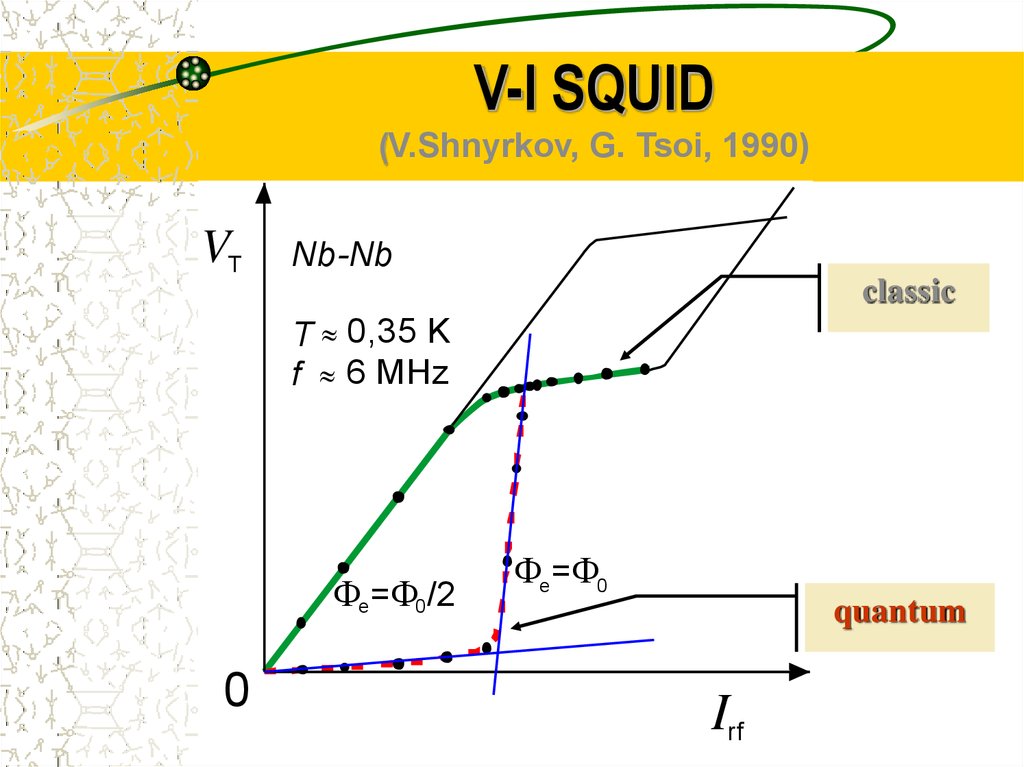
29. V-I SQUID (V.Shnyrkov, G. Tsoi, 1990)
VTNb-Nb
classic
T 0,35 K
f 6 MHz
e = 0 /2
0
e = 0
quantum
Irf
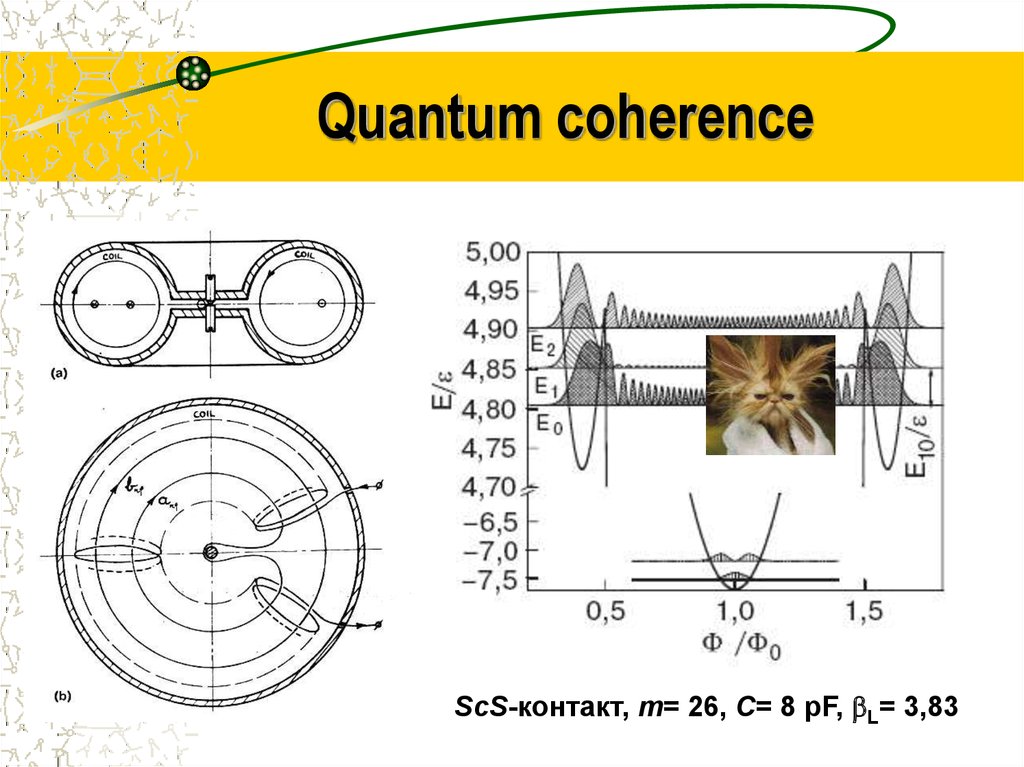
30. Quantum coherence
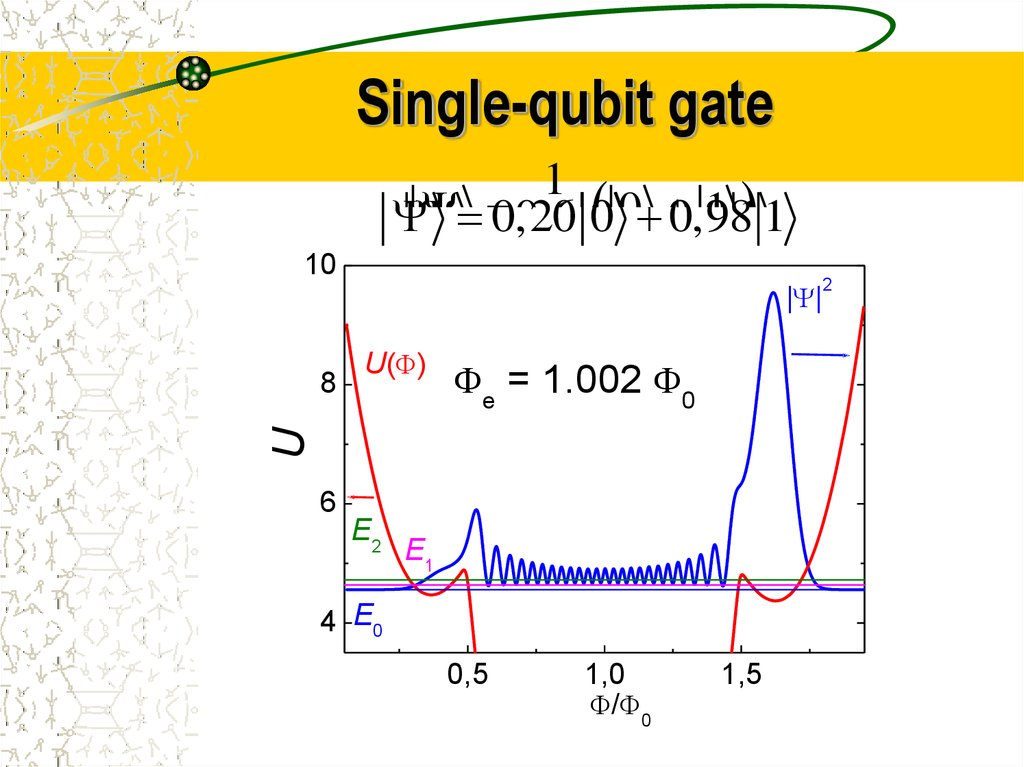
ScS-контакт, m= 26, C= 8 pF, L= 3,8331. Single-qubit gate
1010
10
2
| 2 |
2|
|
| |
UU(
( ) )
U
U
U
88
8
1
0,20
1 1 1
0,6 0 0
0,8
0,98
2
e = 1.002 0
e = 1.001 0
e = 0
666
EEE
22E
2
1 E1
E
1
444EEE
0 00
0,5
0,5
0,5
1,0
1,0
1,0
/ 0
//
00
1,5
1,5
1,5
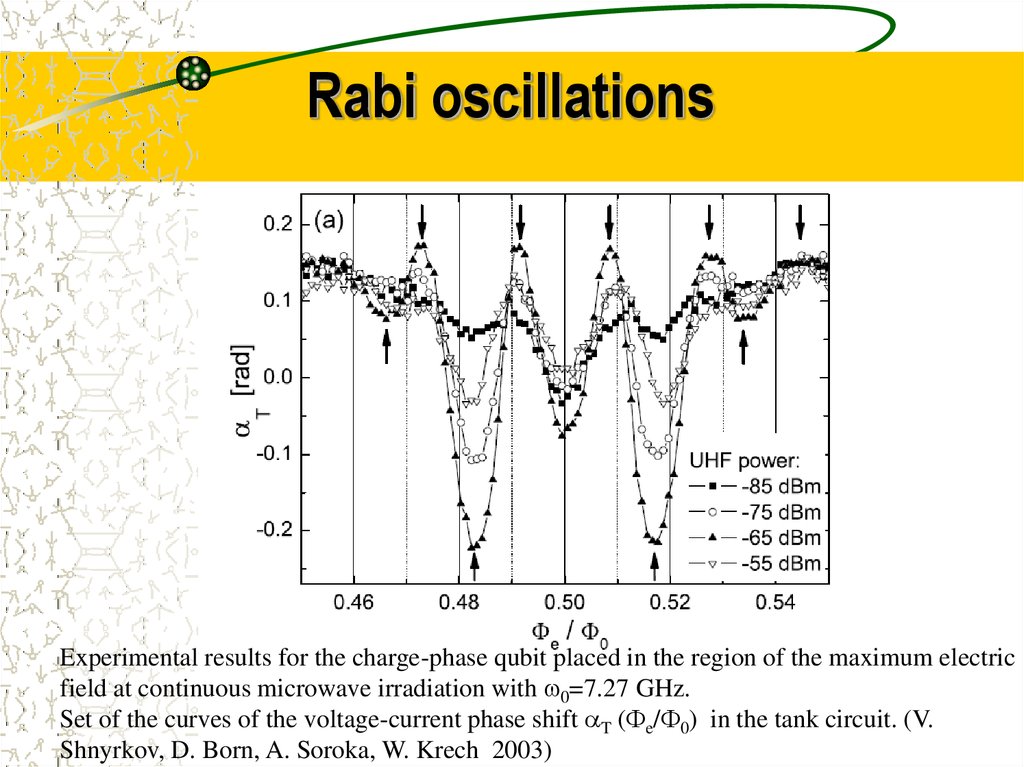
32. Rabi oscillations
Experimental results for the charge-phase qubit placed in the region of the maximum electricfield at continuous microwave irradiation with w0=7.27 GHz.
Set of the curves of the voltage-current phase shift T ( e/ 0) in the tank circuit. (V.
Shnyrkov, D. Born, A. Soroka, W. Krech 2003)
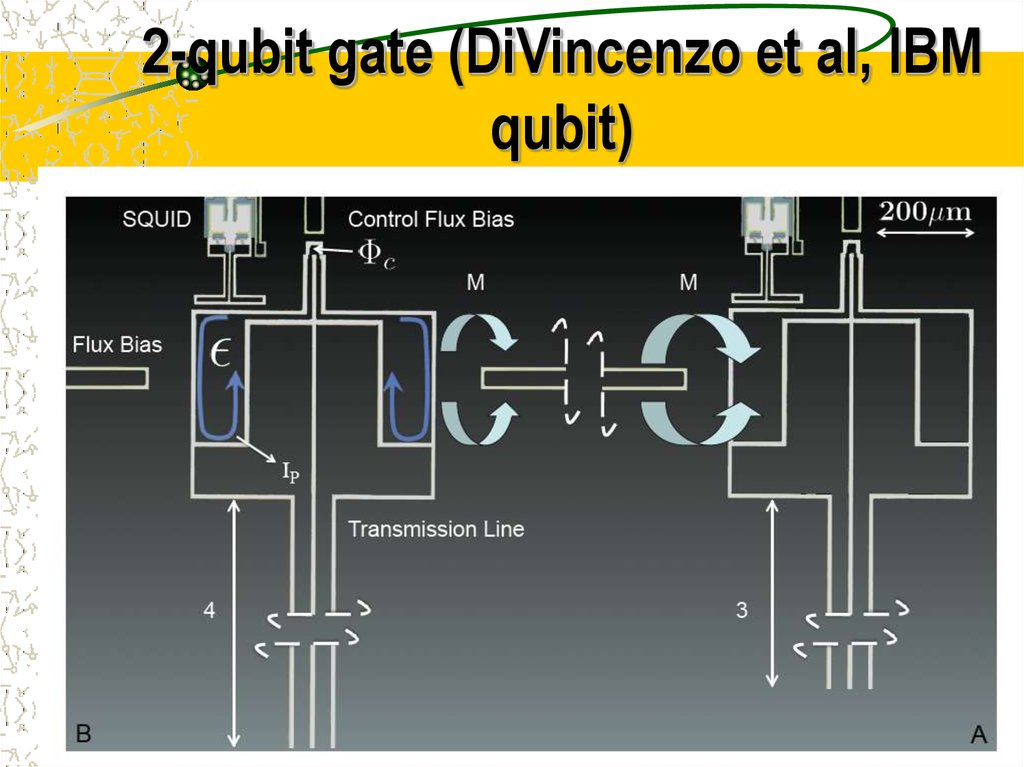
33. 2-qubit gate (DiVincenzo et al, IBM qubit)
34. Find the period: Shor’s algorithm
2n 1x f ( x)
x 0
x
x a f ( x)
f ( x)
x a
a
Hˆ
y
x
f ( x a ) f ( x)
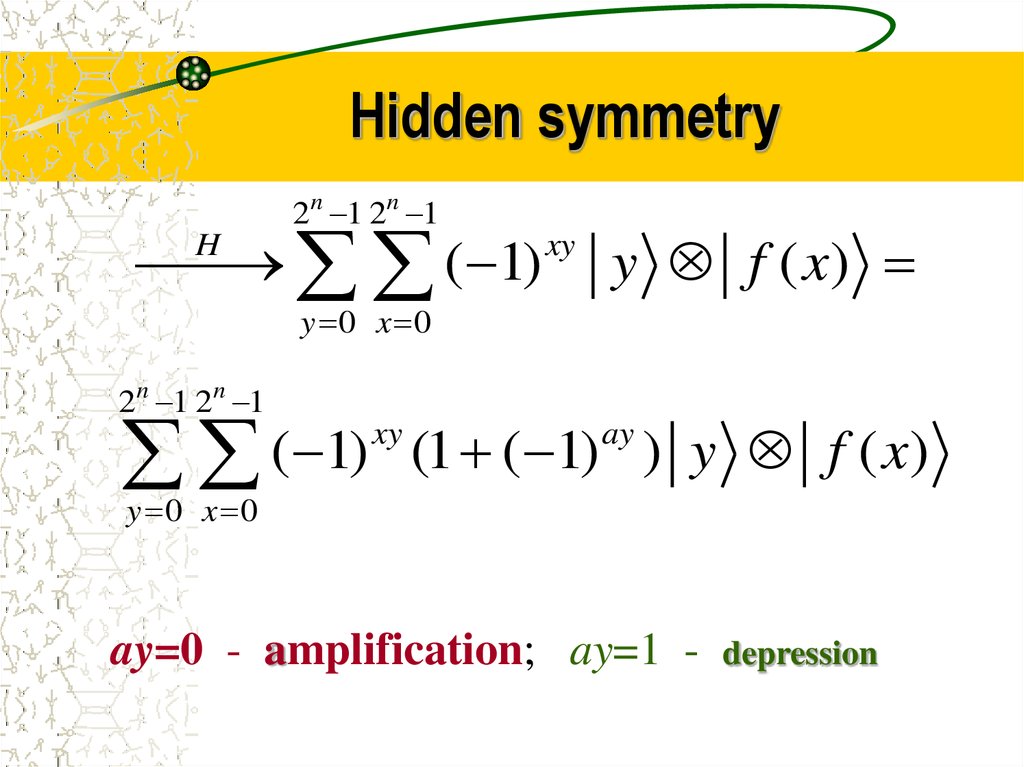
35. Hidden symmetry
2n 1 2n 1( 1)
H
xy
y f ( x)
y 0 x 0
2n 1 2n 1
( 1)
xy
(1 ( 1) ) y f ( x)
ay
y 0 x 0
ay=0 - amplification; ay=1 -
depression
36. Database search
Classic algorithm : 2n =NQuantum algorithm: 2n/2 = N
Unsorted database
s
Merlin
N
1
N
x 0
x
1
N
0..00
w ??..?
... 1..11
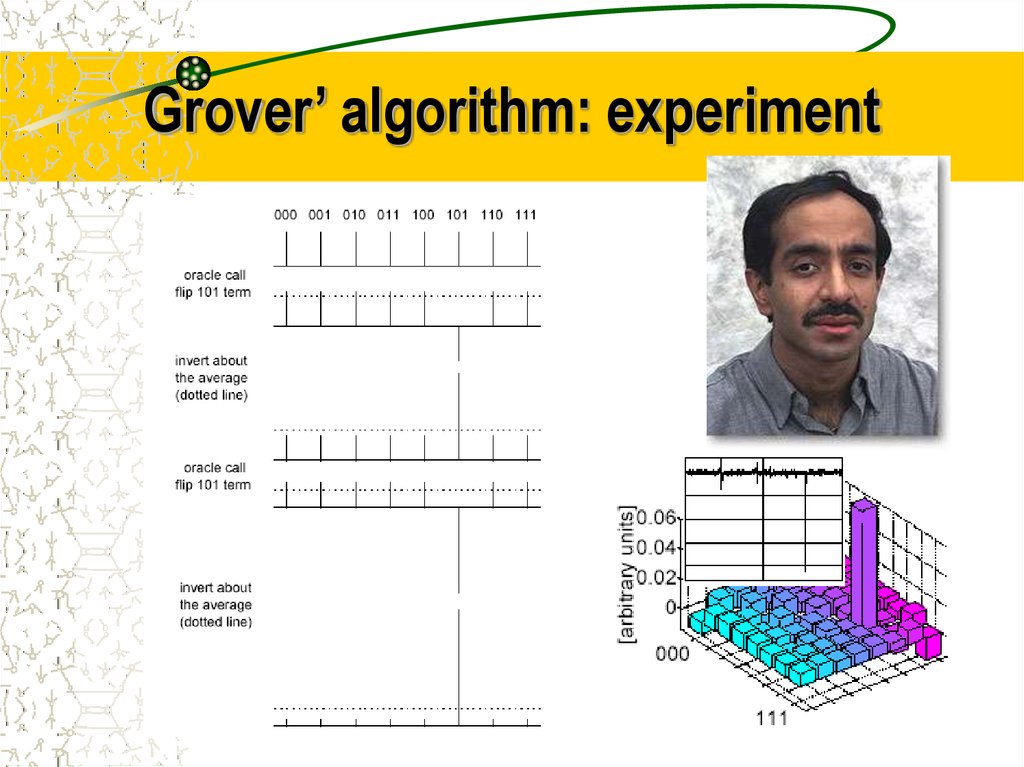
37. Grover’ algorithm
InputFlip (Merlin)
Uw 1 2 w w
Mirroring
U s 2 s s 1
38. Grover’ algorithm: experiment
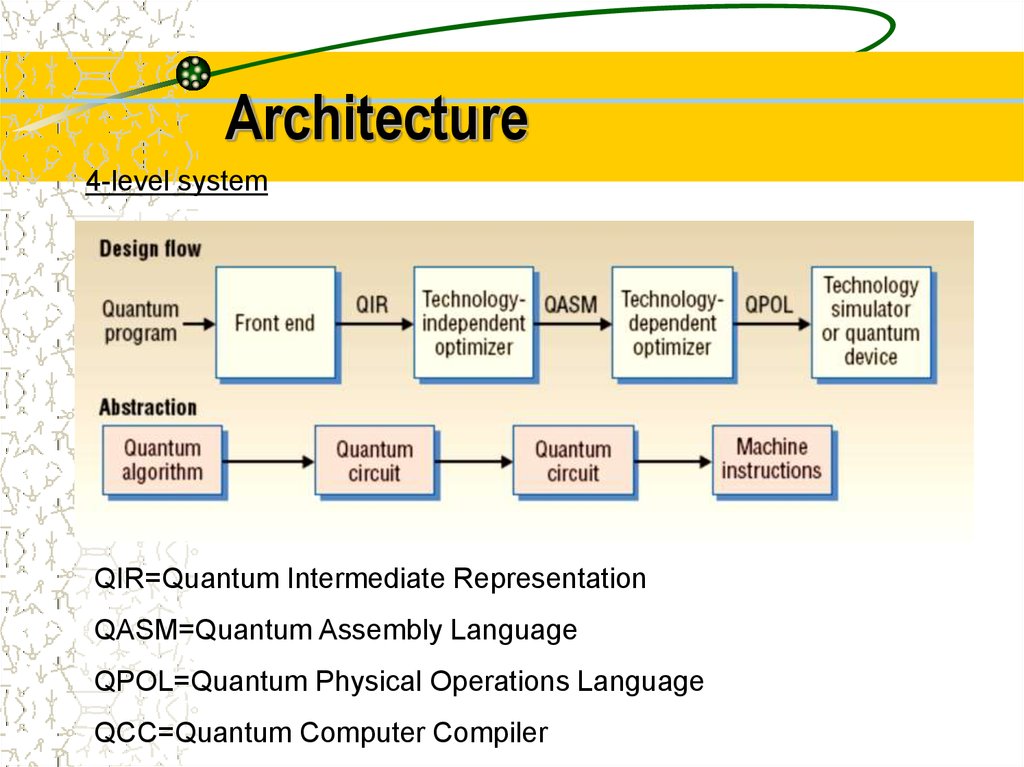
39. Architecture
4-level systemQIR=Quantum Intermediate Representation
QASM=Quantum Assembly Language
QPOL=Quantum Physical Operations Language
QCC=Quantum Computer Compiler
40. Quantum computer: challenges
Decoherence (state instability)Scaling (few number of qubits)
Input-output control
Extreme conditions (T=10 mK, …)
New math algorithms development
Consumer friendly implementation
Weak measurement
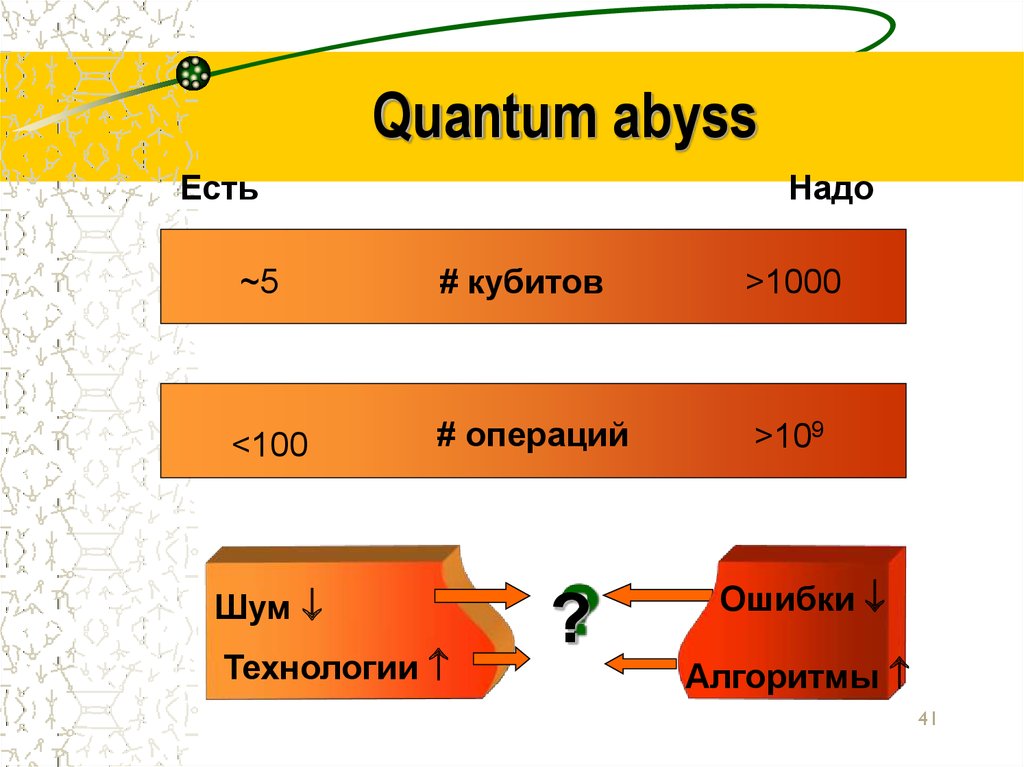
41. Quantum abyss
ЕстьНадо
~5
# кубитов
>1000
<100
# операций
>109
Шум
Технологии
?
Ошибки
Алгоритмы
41
42. When, Where, Who & hoW?
When, Where, Who & hoW?2 qb — 1999, 7 qb — 2001, 16 qb — 2007,
NP — 2012,1000 qb —2015, on-table -- 20xx?
~ 1000 experimental groups over the world
Physics, math, computer science, engineering?
Semi- or super-conductors or?
43. Alumni
Sergii StrelchukVadym Kliuchnikov
Junior Research Fellow @ Centre for
Quantum Information and Foundations,
UC
http://www.qi.damtp.cam.ac.uk/node/72
Post doc researcher @ Microsoft
Research
http://research.microsoft.com/enus/people/vadym/





















 physics
physics








