How Much Information Is In A Quantum State?

1. How Much Information Is In A Quantum State?

Scott Aaronson
MIT

2.

Computer Scientist / Physicist
Nonaggression Pact
You accept that, for this talk:
• Polynomial vs. exponential is the basic dichotomy
of the universe
• “For all x” means “for all x”
In return, I will not inflict the following
computational complexity classes on you:
#P AM AWPP BQP BQP/qpoly MA NP P/poly PH
PostBQP PP PSPACE QCMA QIP QMA SZK YQP

3.

So, how much information is in a quantum state?
An infinite amount, of course, if you want to specify
the state exactly…
1
0
0
C 2
Life is too short for infinite precision

4.

A More Serious Point
In general, a state of n possibly-entangled qubits takes
~2n bits to specify, even approximately
x x
x 0,1
Spin-½ particles
n
To a computer scientist, this is arguably the
central fact about quantum mechanics
But why should we worry about it?

5.

Answer 1: Quantum
State Tomography
Task: Given lots of copies of an unknown quantum state ,
produce an approximate classical description of
Not something I just made up!
“As seen in Science & Nature”
Well-known problem: To do tomography on an entangled
state of n spins, you need ~cn measurements
Current record: 8 spins / ~656,000 experiments (!)
This is a conceptual problem—not just a practical one!

6.

Answer 2: Quantum Computing Skepticism
Levin
Goldreich
‘t Hooft
Davies
Wolfram
Some physicists and computer scientists believe quantum
computers will be impossible for a fundamental reason
For many of them, the problem is that a quantum computer
would “manipulate an exponential amount of information”
using only polynomial resources
But is it really an exponential amount?

7.

Today we’ll tame the exponential beast
Idea: “Shrink quantum states down to reasonable
size” by viewing them operationally
Analogy: A probability distribution over n-bit strings also takes
~2n bits to specify. But that fact seems to be “more about the
map than the territory”
• Setting the stage: Holevo’s Theorem and random access codes
• Describing a state by postselected measurements [A. 2004]
• “Pretty good tomography” using far fewer measurements [A. 2006]
- Numerical simulation [A.-Dechter, in progress]
• Encoding quantum states as ground states of simple Hamiltonians
[A.-Drucker 2009]

8.

Alice
Bob
Theorem [Holevo 1973]: By sending an n-qubit state
, Alice can communicate no more than n classical
bits to Bob (or 2n bits assuming prior entanglement)
How can that be? Well, Bob has to measure , and
measuring makes most of the wavefunction go poof…
Lesson: “The linearity of QM helps
tame the exponentiality of QM”

9. The Absent-Minded Advisor Problem

Can you give your graduate student a quantum state
with n qubits (or 10n, or n3, …)—such that by measuring
in a suitable basis, the student can learn your answer
to any one yes-or-no question of size n?
NO [Ambainis, Nayak, Ta-Shma, Vazirani 1999]
Indeed, quantum communication is no better than
classical for this problem as n

10.

On the Bright Side…
Suppose Alice wants to describe an n-qubit state to
Bob, well enough that for any 2-outcome measurement
E, Bob can estimate Tr(E )
Then she’ll need to send ~cn bits, in the worst case.
But… suppose Bob only needs to be able to estimate
Tr(E ) for every measurement E in a finite set S.
Theorem (A. 2004): In that case, it suffices for
Alice to send ~n log n log|S| bits

11.

ALL MEASUREMENTS
PERFORMABLE
ALL MEASUREMENTS
USING ≤n2 QUANTUM GATES

12.

How does the theorem work?
I 321
Alice is trying to describe the quantum state to Bob
In the beginning, Bob knows nothing about , so he guesses it’s
the maximally mixed state 0=I
Then Alice helps Bob improve his guess, by repeatedly telling
him a measurement Et S on which his guess t-1 badly fails
Bob lets t be the state obtained by starting from t-1, then
performing Et and postselecting on the right outcome

13.

Claim: After only O(n) of these learning steps, Bob gets a
state T such that Tr(E T) Tr(E ) for all measurements E S.
Proof Sketch: For simplicity, assume =| | is pure and
Tr(E ) is ≤1/n2 or 1-1/n2 for all E S.
Let p be the probability that E1,E2,…,ET all yield the desired
outcomes. By assumption, p is at most (say) (2/3)T
On the other hand, if Bob had made the lucky guess
0=| |, then p would’ve been at least (say) 0.9
But we can decompose I as an equal mixture of | and 2n-1
other states orthogonal to | ! Hence p 0.9/2n
0.9/2n ≤ (2/3)T T=O(n)
Conclusion: Alice can describe to Bob by telling him its
behavior on E1,E2,…,ET. This takes O(n log|S|) bits

14.

Discussion
We’ve shown that for any n-qubit state and set S of
observables, one can “compress” the measurement data
{Tr(E )} E S into a classical string x of only Õ(nlog|S|) bits
Just two tiny problems…
1.Computing x seems astronomically hard
2.Given x, estimating Tr(E ) also seems astronomically hard
I’ll now state the “Quantum Occam’s Razor Theorem,”
which at least addresses the first problem…

15.

Quantum Occam’s Razor
Theorem
Let be an unknown quantum state of n spins
Suppose you just want to be able to estimate Tr(E ) for most
measurements E drawn from some probability measure D
Then it suffices to do the following, for some m=O(n):
1. Choose E1,…,Em independently from D
2. Go into your lab and estimate Tr(Ei ) for each 1≤i≤m
3. Find any “hypothesis state” such that Tr(Ei ) Tr(Ei )
for all 1≤i≤m

16.

Theorem [A. 2006]: Provided
C n
1
2 1
m 4 4 log
log (C a constant)
and
Tr Ei Tr Ei
2
7
states are
for all i, you’ll “Quantum
be guaranteed that
PAC-learnable”
Pr Tr E Tr E 1 ,
E~D
with probability at least 1- over the choice of E1,…,Em.
Proof combines Ambainis et al.’s result on the impossibility
of quantum compression with some power tools from
classical computational learning theory

17.

Remark 1: To do this “pretty good tomography,” you don’t
need any prior assumptions about ! (No Bayesian nuthin’...)
Removes a lot of conceptual problems...
Instead, you assume a distribution D over measurements
Might be preferable—after all, you can control which
measurements to apply, but not what is
Remark 2: Given the measurement data Tr(E1 ),…,Tr(Em ),
finding a hypothesis state consistent with it could still be
an exponentially hard computational problem
Semidefinite / convex programming in 2n dimensions
But this seems unavoidable: even finding a classical
hypothesis consistent with data is conjectured to be hard!

18.

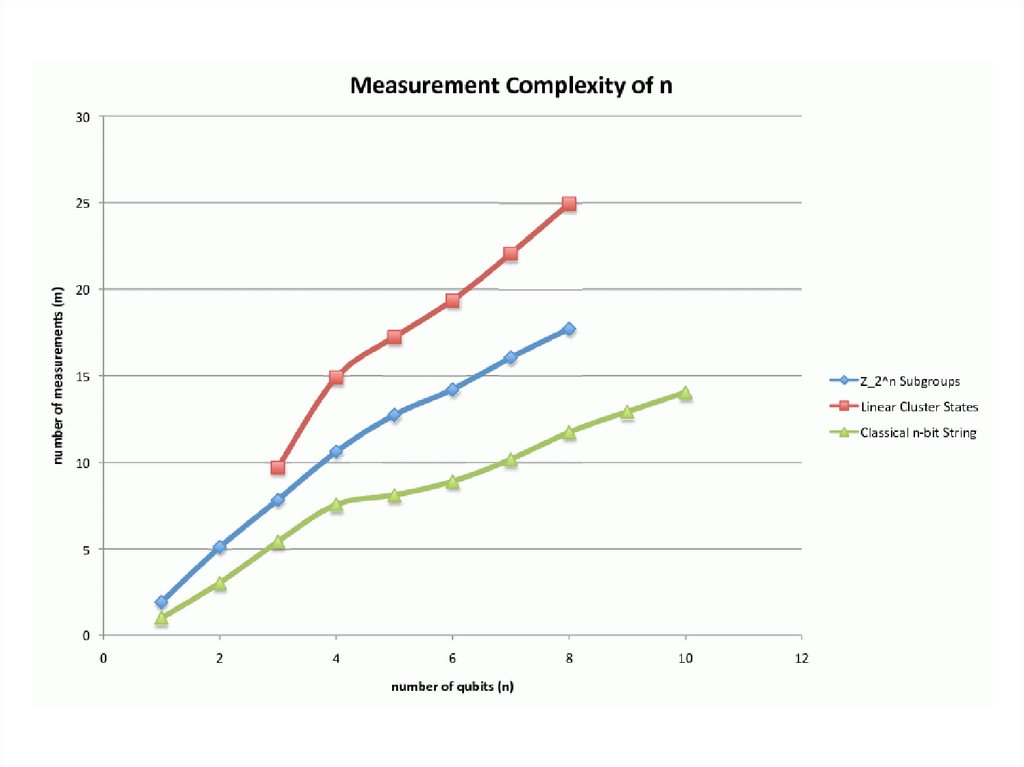
Numerical Simulation
[A.-Dechter, in progress]
We implemented the “pretty-good tomography” algorithm
in MATLAB, using a fast convex programming method
developed specifically for this application [Hazan 2008]
We then tested it (on simulated data) using MIT’s
computing cluster
We studied how the number of sample measurements m
needed for accurate predictions scales with the number of
qubits n, for n≤10
Result of experiment: My theorem appears to be true

19.

20.

Recap: Given an unknown n-qubit entangled quantum state ,
and a set S of two-outcome measurements…
Learning theorem: “Any hypothesis state consistent with a
small number of sample points behaves like on most
measurements in S”
Postselection theorem: “A particular state T (produced by
postselection) behaves like on all measurements in S”
Dream theorem: “Any state that passes a small number of
tests behaves like on all measurements in S”
[A.-Drucker 2009]: The dream theorem holds
Caveat: will have more qubits than , and in general be a very different state
Proof combines Quantum Occam’s Razor Theorem with a new
classical result about “isolatability” of functions

21.

A “Practical” Implication
It’s the year 2500. Everyone and her grandfather has a
personal quantum computer.
You’re a software vendor who sells “magic initial states”
that extend quantum computers’ problem-solving abilities.
Amazingly, you only need one kind of state in your store:
ground states of 1D nearest-neighbor Hamiltonians!
UNIVERSAL RESOURCE STATE
Reason: Finding ground states of 1D spin systems is known to
be “universal” for quantum constraint satisfaction problems
[Aharonov-Gottesman-Irani-Kempe 2007], building on [Kitaev 1999]

22.

Summary
In many natural scenarios, the “exponentiality” of quantum
states is an illusion
That is, there’s a short (though possibly cryptic) classical
string that specifies how a quantum state behaves, on any
measurement you could actually perform
Applications: Pretty-good quantum state tomography,
characterization of quantum computers with “magic initial
states”…
Biggest open problem: Find special classes of quantum
states that can be learned in a computationally efficient way
“Experimental demonstration” would be nice too

23.

www.scottaaronson.com
(/papers /talks /blog)
Postselection theorem: quant-ph/0402095
Learning theorem: quant-ph/0608142
Ground state theorem, numerical simulations: “in
preparation”