Basics of thermodynamics & kinetics

1.

PROTEIN PHYSICS
LECTURES 7-8
Basics of thermodynamics & kinetics

2.

THERMODYNAMISC
&
STATISTICAL PHYSICS

3.

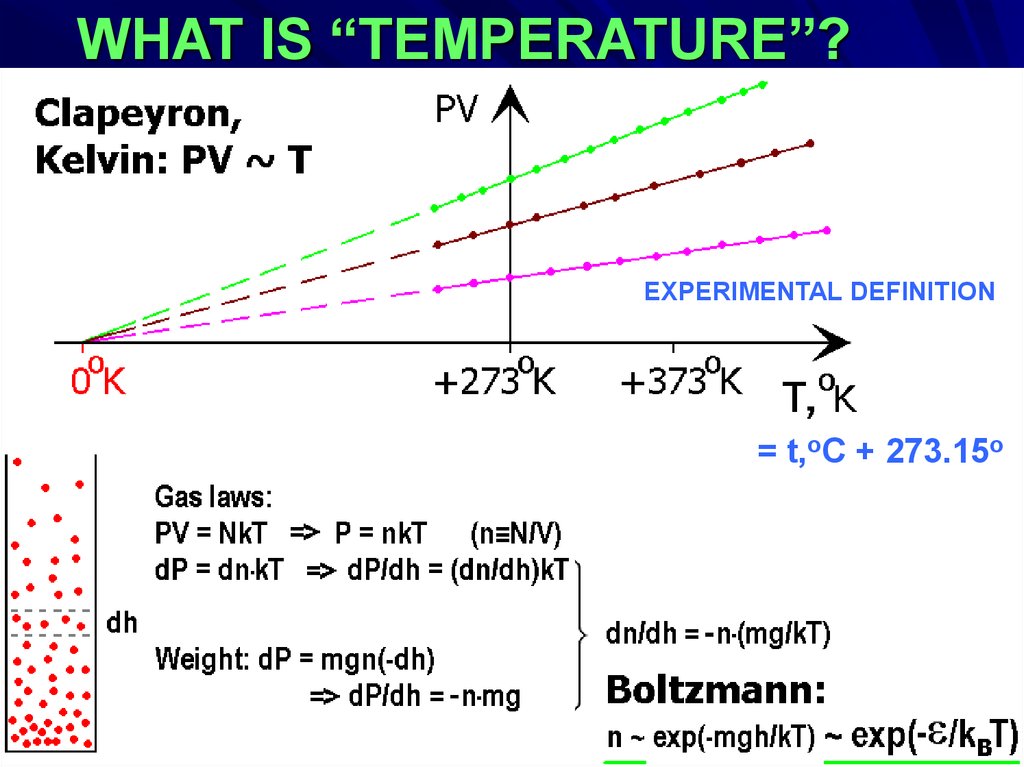
WHAT IS “TEMPERATURE”?
EXPERIMENTAL DEFINITION :
EXPERIMENTAL DEFINITION
= t,oC + 273.15o

4.

Benoît Paul Émile Clapeyron (1799 – 1864)
William Thomson, 1st Baron Kelvin (1824 -1907)
Ludwig Eduard Boltzmann (1844 – 1906)

5.

WHAT IS “TEMPERATURE”?
THEORY
S ~ ln[M]
Closed
system:
energy
E = const
CONSIDER: 1 state of “small part” with & all
states of thermostat with E- . Mall(E- ) = 1 • Mt(E- )
k • ln[Mt(E- )] St(E- ) St(E) - •(dSt/dE)|E
Mt(E- ) exp[St(E)/k] • exp[- •(dSt/dE)|E/k]
conclusions

6.

COMPARE:
Probability1( 1) = Mt(E- 1)/M(E) =
exp[- 1• (dSt/dE)|E/k]
(GIBBS)
and
Probability1( 1) = exp(- 1/kBT) (BOLTZMANN)
One has:
(dSt/dE)|E = 1/T
k
=
k
B
______________________________________________________________
-kBT,
M M exp(1) M 2.72

7.

Josiah Willard Gibbs
(1839 –1903)
Joseph Liouville
(1809 - 1882)
Яков Григорьевич Синай, 1935
Abel Prize 2014
“…связь между порядком и хаосом…”
1/r3

8.

(dSth/dE) = 1/ T
P1( 1) ~ exp(- 1/kBT)
Pj( j) = exp(- j/kBT)/Z(T);
j Pj( j) 1
Z(T) = i exp(- i/kBT) partition function
СТАТИСТИЧЕСКАЯ СУММА

9.

Along tangent: S-S(E1) = (E-E1)/T1
i.e., F = E - T1S = const (= F1 = E1 - T1S1)
stable
Unstable (explodes, v → inf.)
Unstable (falls)
unstable

10.

Separation of potential and kinetic energies
in classic (non-quantum) mechanics:
P( ) ~ exp(- /kBT) // Classic: = COORD + KIN
KIN = mv2/2 : does not depend on coordinates
Potential energy COORD: depends only on coordinates
P( ) ~ exp(- COORD/kBT) • exp(- KIN/kBT)
Z(T) = ZCOORD(T)•ZKIN(T)
F(T) = FCOORD(T)+FKIN(T)
========================================================================================================================
Elementary volume: (mv) x ħ ( x)3 (ħ/|mv|)3
2/[mk T])3/2
=
(ħ
B
(mv) m|v|, and |mv| (mk T)1/2
B

11.

IN THERMAL EQUILIBRIUM:
TCOORD = TKIN = Touter
We may consider further
only potential energy:
E ECOORD
M MCOORD
S(E) SCOORD(ECOORD )
F(E) FCOORD , etc.

12.

TRANSITIONS:
THERMODYNAMICS

13.

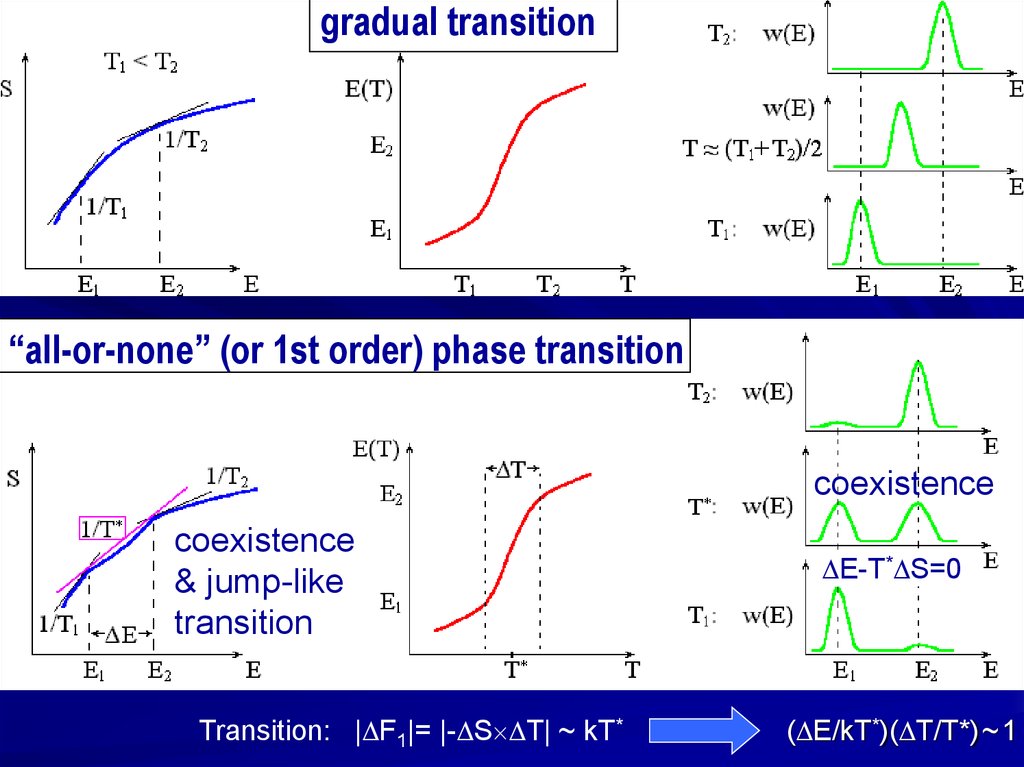
gradual transition
“all-or-none” (or 1st order) phase transition
coexistence
coexistence
& jump-like
transition
Transition: | F1|= |- S T| ~ kT*
E-T* S=0
( E/kT*)( T/T*)~ 1

14.

Second order phase transition
change
Recently observed in proteins;
rare case

15.

LANDAU: Helix-coil transition:
NOT 1-s order phase transition
Melting:
1-s order phase transition
N
n
N
n
Helix & coil: 1D objects
Ice & water: 3D objects
Fhelix_n = Const + n f
FICE_n = C n2/3 + n f
1D interface
3D interface
Mid-transition: f = 0
Shelix_n ~ ln(N)
positions
SICE_n ~ ln(N)
N : very large; n ~ N, <<1 (e.g., ~0.001)
Const << ln(N)
2/3 N2/3 >> ln(N)
phases mix
phases do not mix

16.

Лев Давидович Ландау
(1908 - 1968)
Нобелевская Премия 1962

17.

TRANSITIONS:
KINETICS

18.

Not
#
“slowly goes”,
but
climbs, falls
and climbs again…
n
n
n# = n exp(- F#/kBT)
#
falls
TRANSITION TIME:
t0 1 = t0 #1
# (n/n#) = # exp(+ F#/kBT)

19.

20.

- Coil
- Native
Coil
phase separation

21.

PARALLEL REACTIONS:
TRANSITION RATE =
SUM OF RATES
(or: the highest rate)
RATE = 1/ TIME
1/TIME = (1/ # ) exp(- F1#/kBT) + (1/ # ) exp(- F2#/kBT)

22.

#
_#
“downhill”
_
start
t0 … t0 #1 1 + t1 #2 2 + …
“long barrier”
start
finish CONSECUTIVE REACTIONS:
TRANSITION TIME SUM OF TIMES
(or: the highest time)
“long barrier”:
t0 … finish t0 #1 finish + t0 #2 finish + …
steady-state approximation
TIME # exp(+ F1#/kBT) + # exp(+ F2#/kBT) + …

23.

#
main
main #
_
_
“trap”: on
“trap”: out
start
start
finish
finish
TRANSITION TIME IS ESSENTIALLY
EQUAL FOR “TRAPS” AT AND OUT OF
PATHWAYS OF CONSECUTIVE REACTIONS:
TRANSITION TIME SUM OF TIMES
(or: the longest time)

24.

DIFFUSION:
KINETICS

25. Mean kinetic energy of a particle: mv2/2 ~ kBT <> = j Pj(j)  j v2 = (vX2)+(vY2)+(vZ2) Maxwell :

Mean kinetic energy of a particle:
< > = j Pj( j) j
mv2/2 ~ kBT
v2 = (vX2)+(vY2)+(vZ2)
James Clerk
Maxwell :
(1831 –1879)
in 3D

26.

Friction stops a molecule within picoseconds:
m(dv/dt) = -(3 D )v
[Stokes law], or m(dv/dt) = -(kBT/Ddiff)v
[Einstein-Stokes]
D – diameter;
m ~ D3 1g/cm3 – mass;
– viscosity
tkinet 10-13 sec (D/nm)2
in water
Sir George Gabriel Stokes
(1819-1903)
DIFFUSION:
During tkinet the molecule moves by Lkinet ~ v•tkinet
Albert Einstein
(1879-1995)
Then it restores its kinetic energy mv2/2 ~ kBT from thermal
kicks of other molecules, and moves in another random side
CHARACTERISTIC DIFFUSION TIME: nanoseconds

27.

Friction stops a molecule within picoseconds:
tkinet 10-13 sec (D/nm)2
in water
DIFFUSION:
During tkinet the molecule moves by Lkinet ~ v•tkinet
Then it restores its kinetic energy mv2/2 kBT from thermal kicks
of other molecules, and moves in another
→
r1
random side
CHARACTERISTIC DIFFUSION
TIME: nanoseconds
The random walk allows the molecule
to diffuse at distance D (~ its diameter)
within ~(D/L kinet)2 steps, i.e., within
tdifft tkinet•(D/Lkinet)2 = D2/Ddiff
4•10-10 sec (D/nm)3 in water

28. The End

29.

For “small part”:
Pj( j) = exp(- j/kBT)/Z(T);
Z(T) = j exp(- j/kBT)
j Pj( j) = 1
E(T) = < > = j j Pj( j)
if all j =
:
#STATES = 1/P,
i.e.: S(T) = kB ln(1/P)
S(T) = kB<ln(#STATES)> = kB j ln[1/Pj( j)] Pj( j)
F(T) = E(T) - TS(T) = -kBT ln[Z(T)]
STATISTICAL MECHANICS

30.

Thermostat: Tth = dEth/dSth
STATISTICAL
MECHANICS
“Small part”:
Pj( j,Tth) ~ exp(- j/kBTth);
E(Tth) = j j Pj( j,Tth)
S(Tth) = kB j
ln[1/Pj( j,Tth)] Pj( j,Tth)

31.

Along tangent:
S-S(E1) = (E-E1)/T1
i.e.,
F = E - T1S = const (= F1 = E1 - T1S1)

32.

Separation of potential energy
in classic (non-quantum) mechanics:
P( ) ~ exp(- /kBT)
Classic: = COORD + KIN
KIN = mv2/2 : does not depend on coordinates
Potential energy COORD: depends only on coordinates
P( ) ~ exp(- COORD/kBT) • exp(- KIN/kBT)
K exp(- K/kBT): don’t depend on coord.
ZCOORD(T) = Cexp(- C/kBT): depends on coord.
ZKIN(T) =
Z(T) = ZCOORD(T)•ZKIN(T)
F(T) = FCOORD(T)+FKIN(T)
========================================================================================================================
Elementary volume: (mv) x = ħ
( x)3 =(ħ/|mv|)3

33.

P( KIN+ COORD) ~ exp(- COORD/kBT)•exp(- KIN/kBT)
P( COORD) = exp(- COORD/kBT) / ZCOORD(T)
ZCOORD(T) =
Cexp(- C/kBT):
depends ONLY
on coordinates
P( KIN) = exp(- KIN/kBT) / ZKIN(T)
ZKIN(T) =
K exp(- K/kBT): don’t depend on coord.
T<0: unstable (explodes)
< KIN> at T<0
due to
P( KIN) ~ exp(- KIN/kBT)

34.

“all-or-none” (or first order) phase transition
F(T1)
________________