Oscillations. Types of mechanical oscillations free (own)

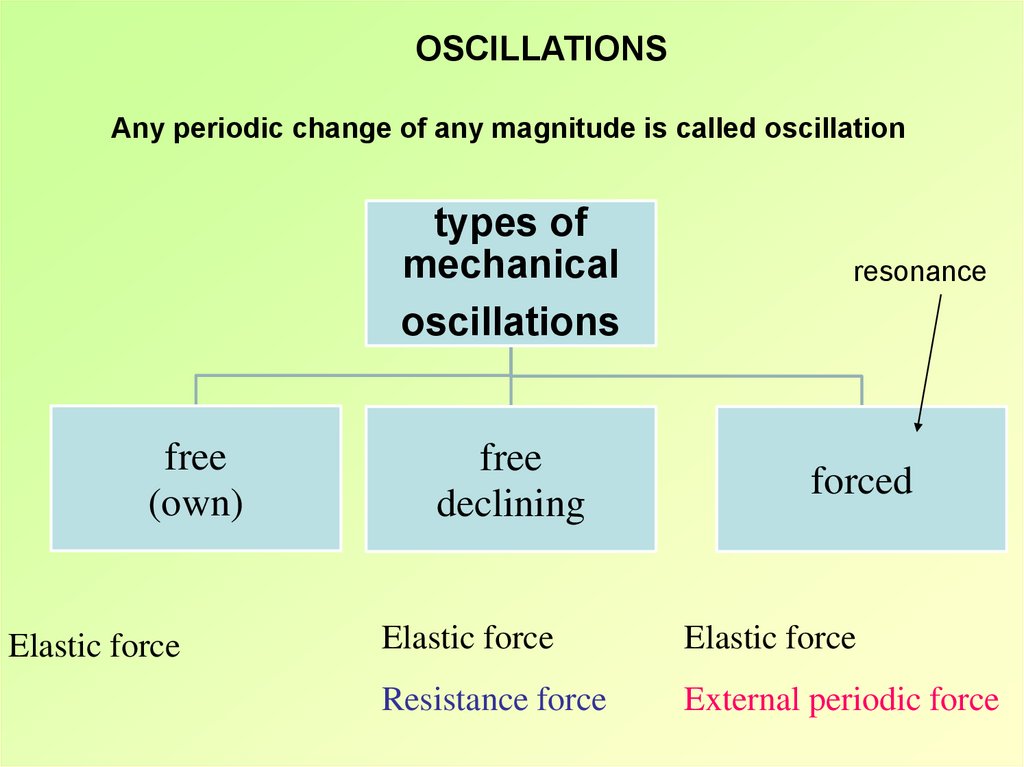
1. resonance

OSCILLATIONS
Any periodic change of any magnitude is called oscillation
types of
mechanical
oscillations
free
(own)
Elastic force
free
declining
resonance
forced
Elastic force
Elastic force
Resistance force
External periodic force

2.

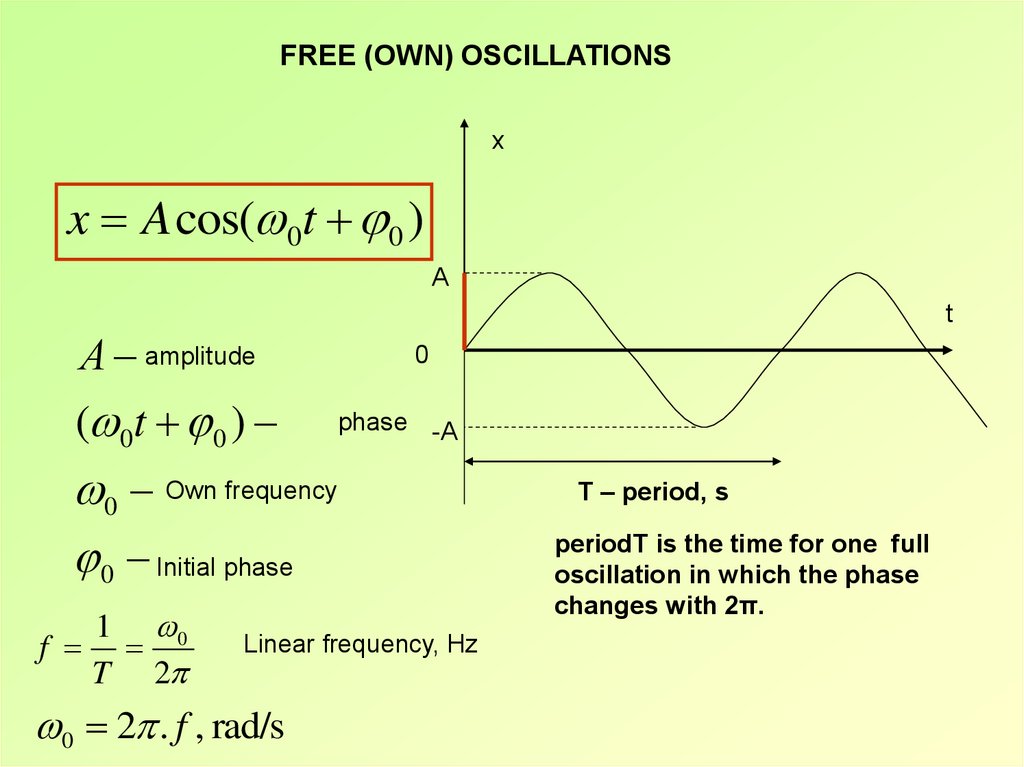
FREE (OWN) OSCILLATIONS
x
x A cos( 0t 0 )
A
А amplitude
( 0t 0 )
t
0
phase -A
0 Own frequency
0 Initial phase
1 0
f
T 2
Linear frequency, Hz
0 2 . f , rad/s
T – period, s
periodТ is the time for one full
oscillation in which the phase
changes with 2π.

3.

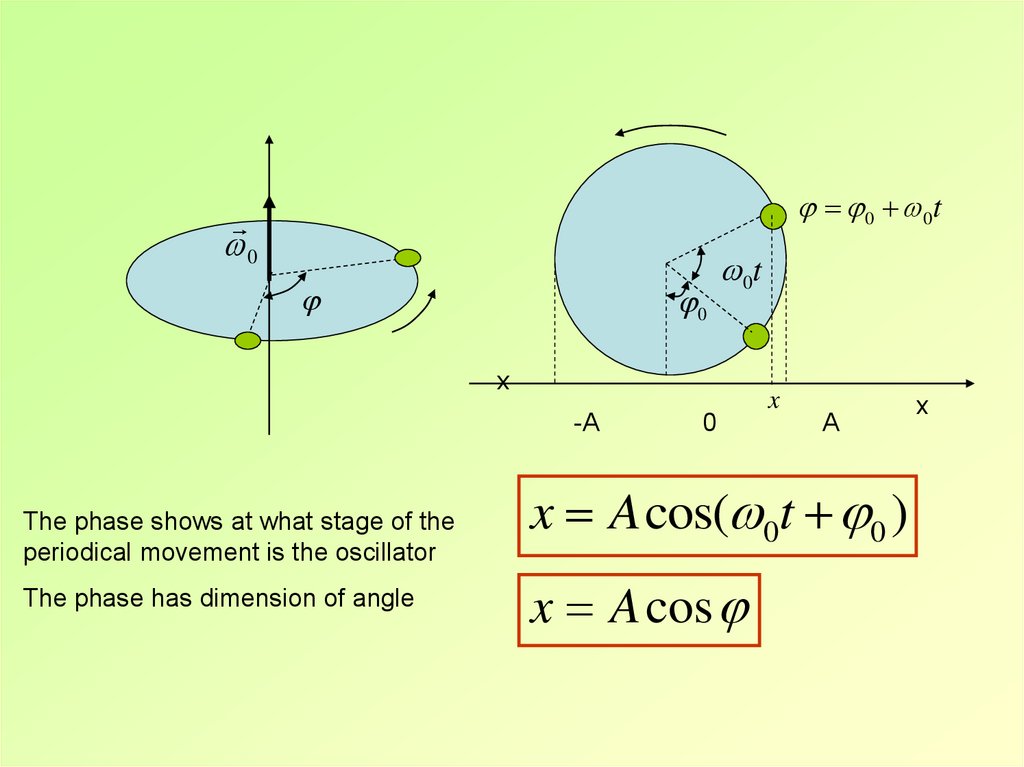
0 0t
0
0
0t
x
-A
The phase shows at what stage of the
periodical movement is the oscillator
The phase has dimension of angle
0
x
A
x A cos( 0t 0 )
x A cos
x

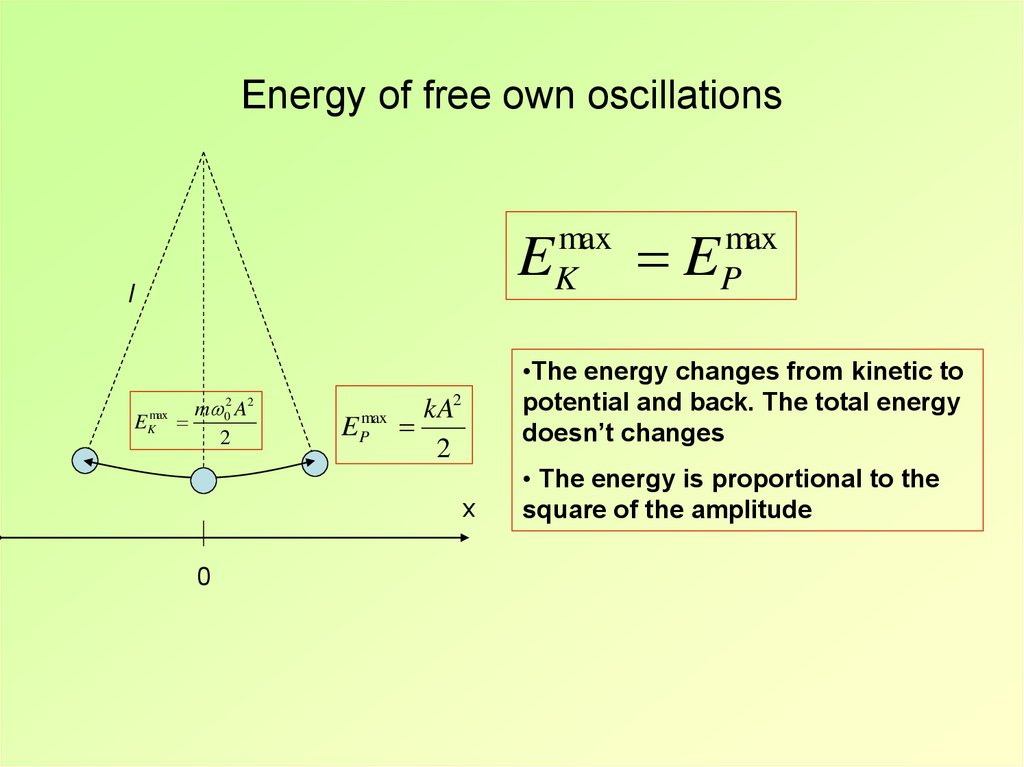
4. Energy of free own oscillations

E
l
E
max
K
m 02 A2
2
E
max
P
E
max
P
•The energy changes from kinetic to
potential and back. The total energy
doesn’t changes
kA2
2
x
0
max
K
• The energy is proportional to the
square of the amplitude

5.

E Ek U
mV 2
kx 2
Ek
; U
2
2
k
k 2m
m
mV 2 m 2 x
V 2 2 x2
E
m(
)
2
2
2
2
x A cos( t 0 )
2
dx
A sin( t 0 )
dt
V 2 A2 2 sin 2 ( t 0 )
V
A2 2 sin 2 ( t 0 ) 2 A2 cos 2 ( t 0 )
E m(
)
2
2
mA2 2
mA2 2
2
2
[(sin ( t 0 ) cos ( t 0 )]
2
2
The sum of kinetic and
potential energy of the
oscillations is constant.

6.

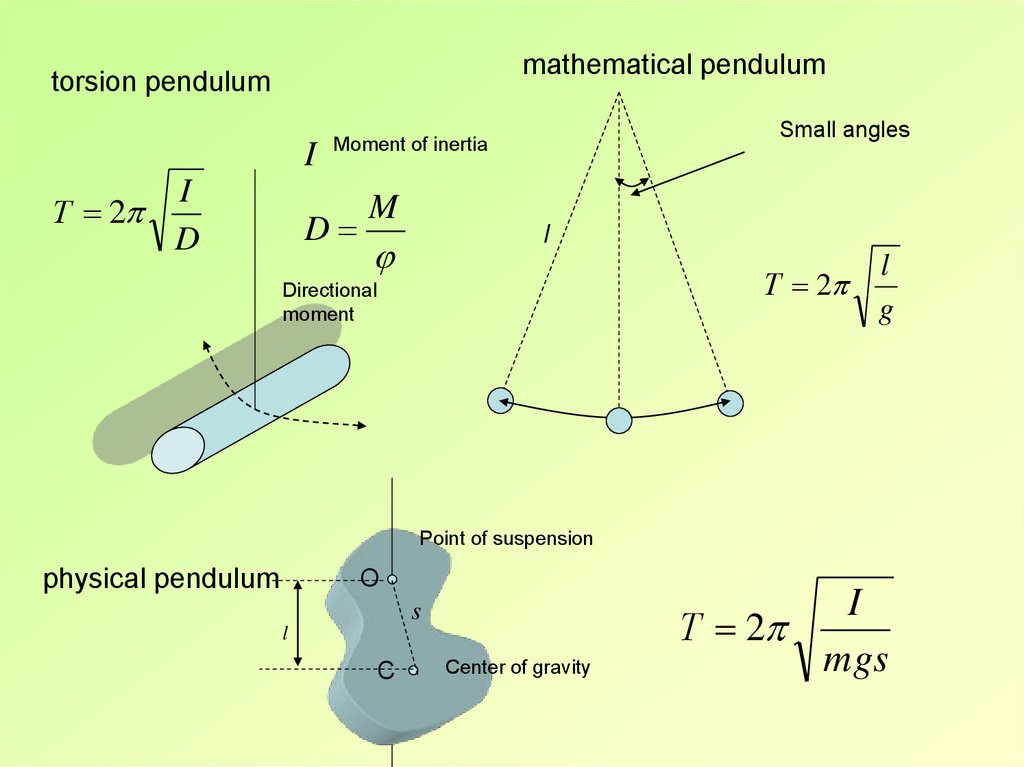
mathematical pendulum
torsion pendulum
I
I
Т 2
D
Small angles
Moment of inertia
D
M
l
Т 2
Directional
moment
l
g
Point of suspension
О
physical pendulum
s
l
C
Center of gravity
I
Т 2
mgs

7.

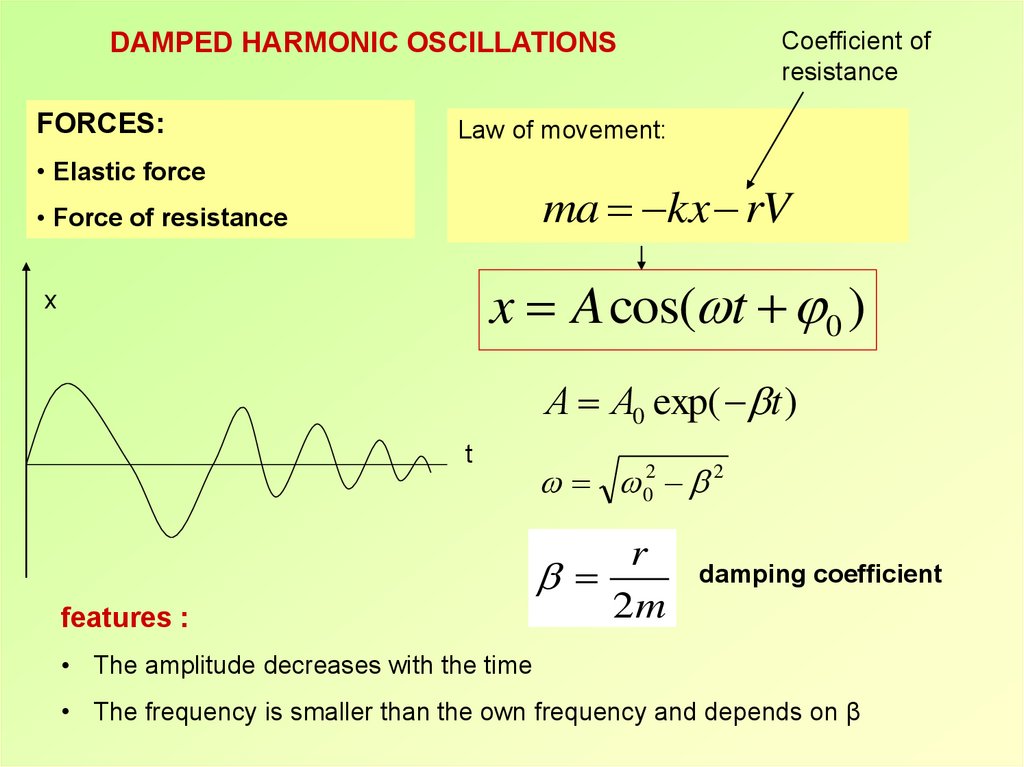
Coefficient of
resistance
DAMPED HARMONIC OSCILLATIONS
FORCES:
Law of movement:
• Elastic force
ma kx rV
• Force of resistance
x A cos( t 0 )
x
А А0 exp( t )
t
features :
02 2
r
2m
damping coefficient
• The amplitude decreases with the time
• The frequency is smaller than the own frequency and depends on β

8.

Important damping parameters:
r
2m
Т
Damping
coefficient
Logarithmic decrement
of damping
А0е t
ln
ln е T T
( t T )
А0е

9.

FORCED OSCILLATIONS
External periodic force causes the oscillations
F F0 cos( t )
Angular
frequency of the
external force
where:
2
2 . f
T
f
- frequency of the external force
Т
- period of the external force
Law of motion:
x A cos( t )

10.

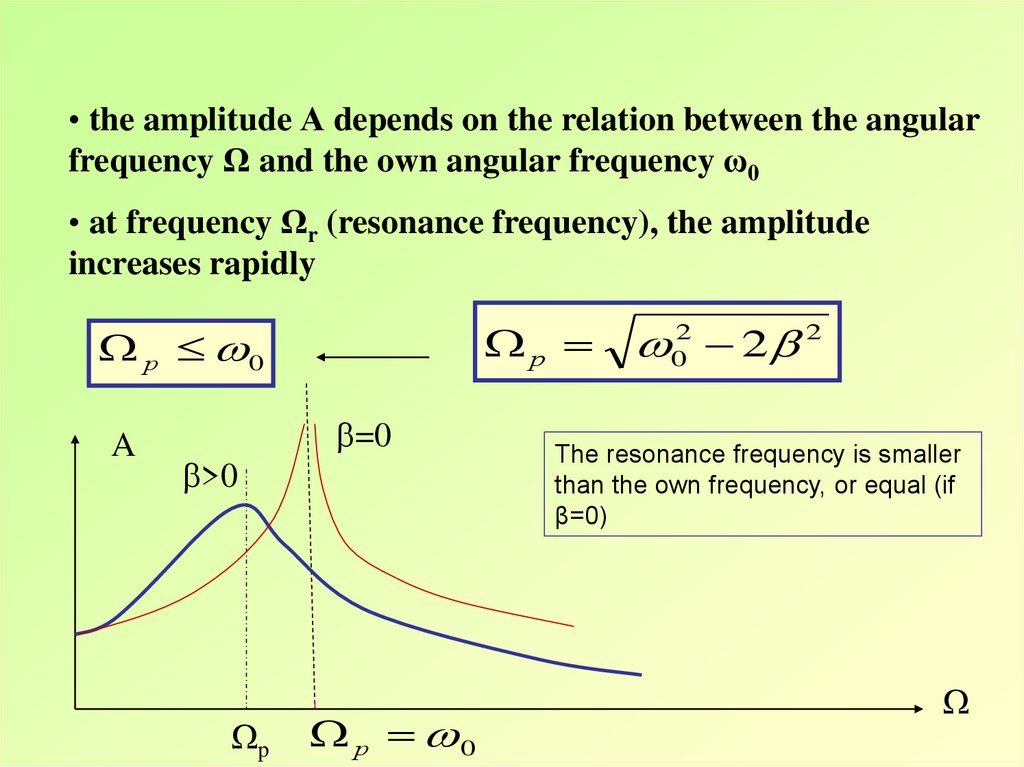
• the amplitude А depends on the relation between the angular
frequency Ω and the own angular frequency ω0
• at frequency Ωr (resonance frequency), the amplitude
increases rapidly
р
р 0
A
>0
p
=0
р 0
02 2 2
The resonance frequency is smaller
than the own frequency, or equal (if
β=0)

11.

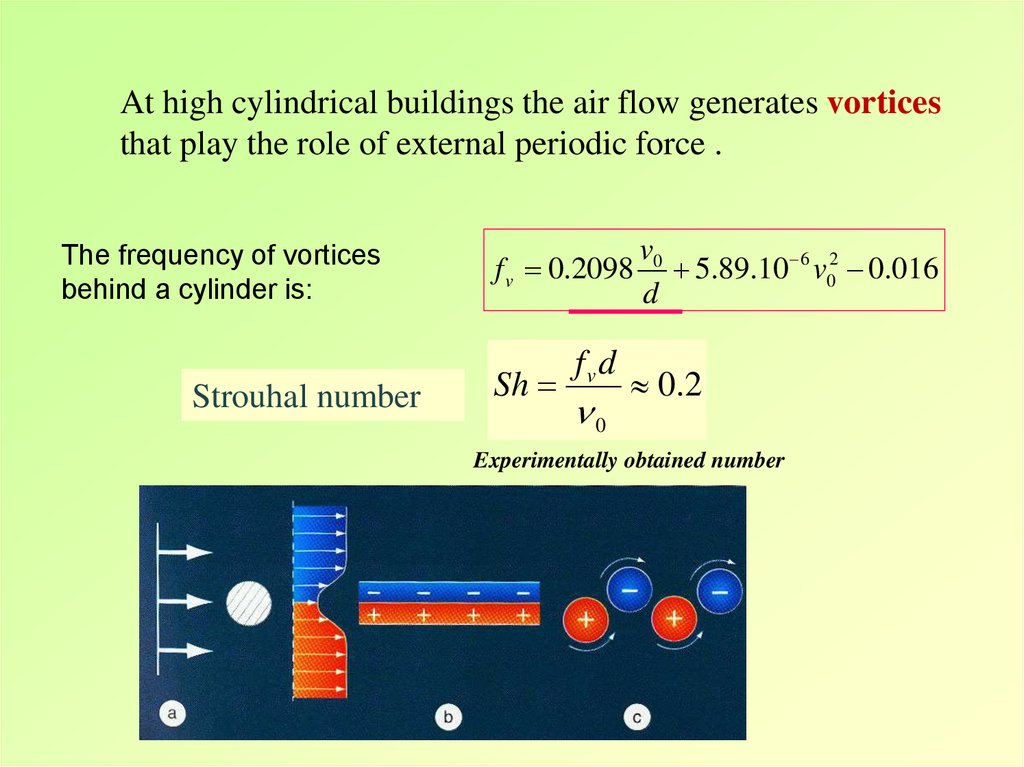
At high cylindrical buildings the air flow generates vortices
that play the role of external periodic force .
The frequency of vortices
behind a cylinder is:
Strouhal number
v0
f v 0.2098 5.89.10 6 v02 0.016
d
Sh
fvd
0
0 .2
Experimentally obtained number

12.

At certain velocity of the wind the frequency of generation
of the vortexes may coincide with the resonance frequency
The destruction of the bridge of Takoma river