Similar presentations:
Secondary structures
1.
PROTEIN PHYSICSLECTURES 9-10
Secondary structures
2.
coil→
r1
L
L
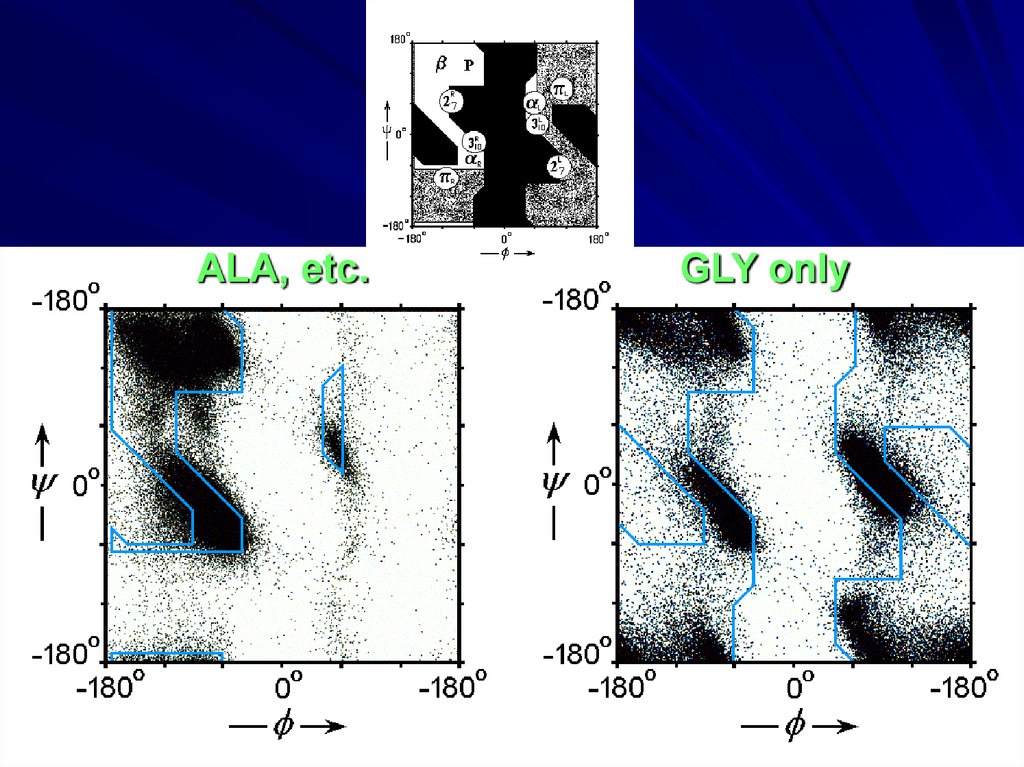
r
<h2> = (Mr)•r = LM•r
1+cos
________
=
L
1– cos
|h| ~ M1/2
V ~ M3/2
3.
Random coil:Werner Kuhn (1899 - 1963)
-helices and -sheets:
Linus Carl Pauling (1901-94)
— Nobel Prizes: 1954, 62
Robert Brainard Corey
(1897 –1971)
Herman Russell Branson
(1914 –1995)
4.
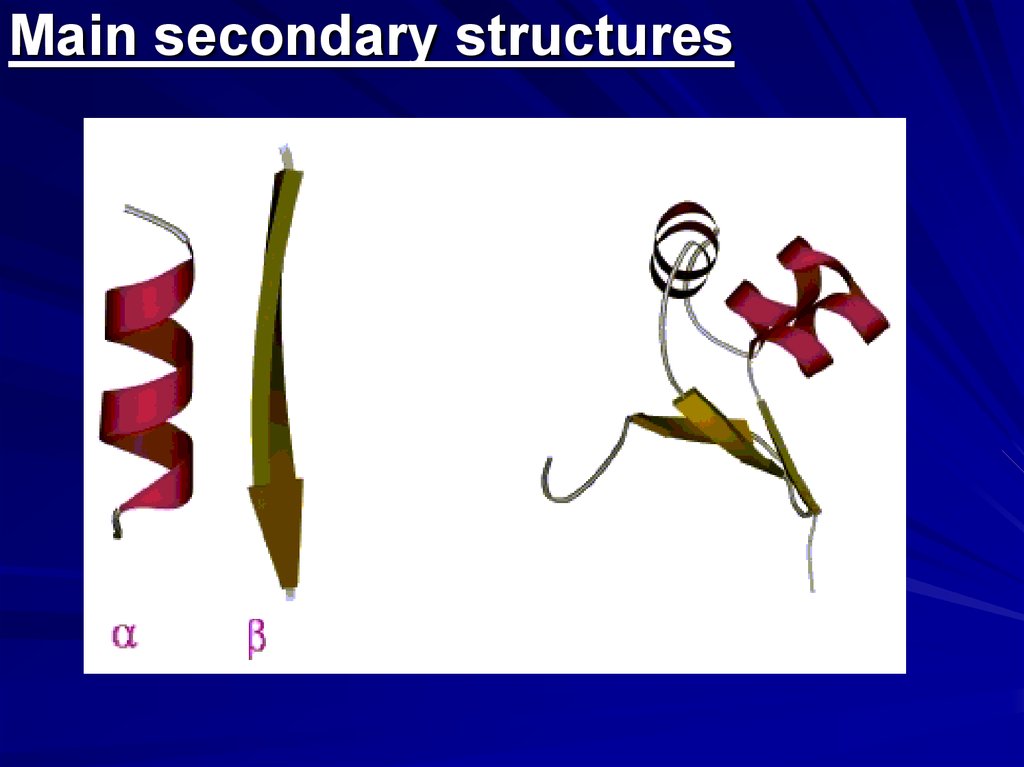
Main secondary structures5.
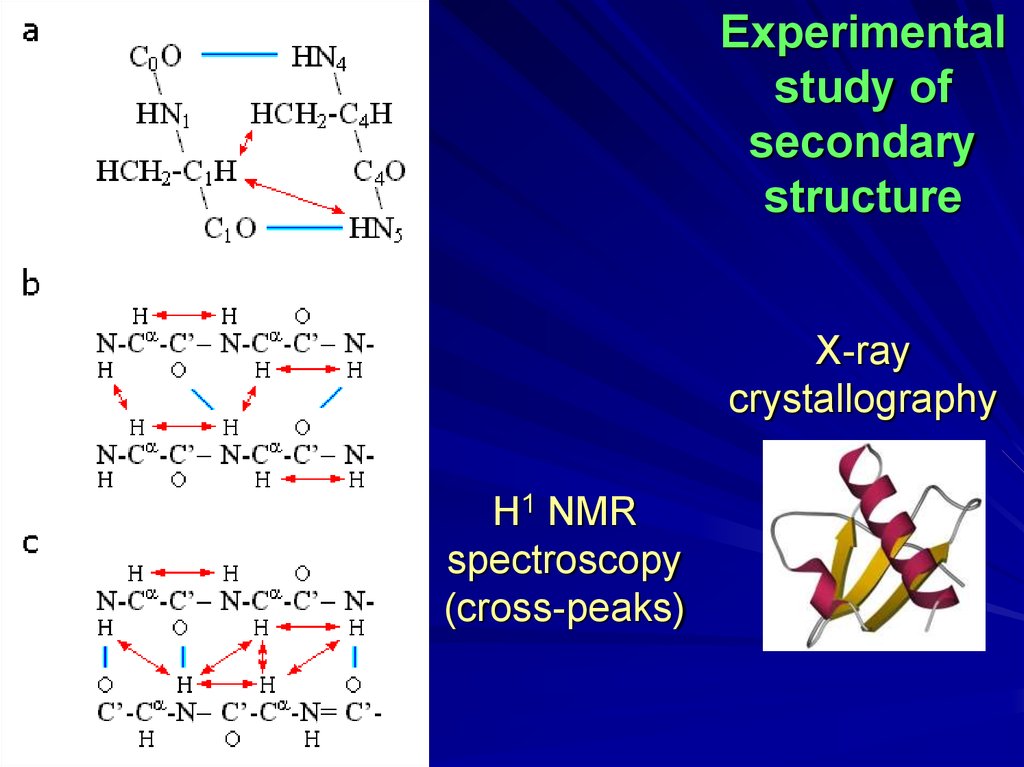
Experimentalstudy of
secondary
structure
X-ray
crystallography
H1 NMR
spectroscopy
(cross-peaks)
6.
Experimental study of secondary structureFar UV CD spectra
(peptide groups)
IR spectra
(“amid I”, C=O bond)
7.
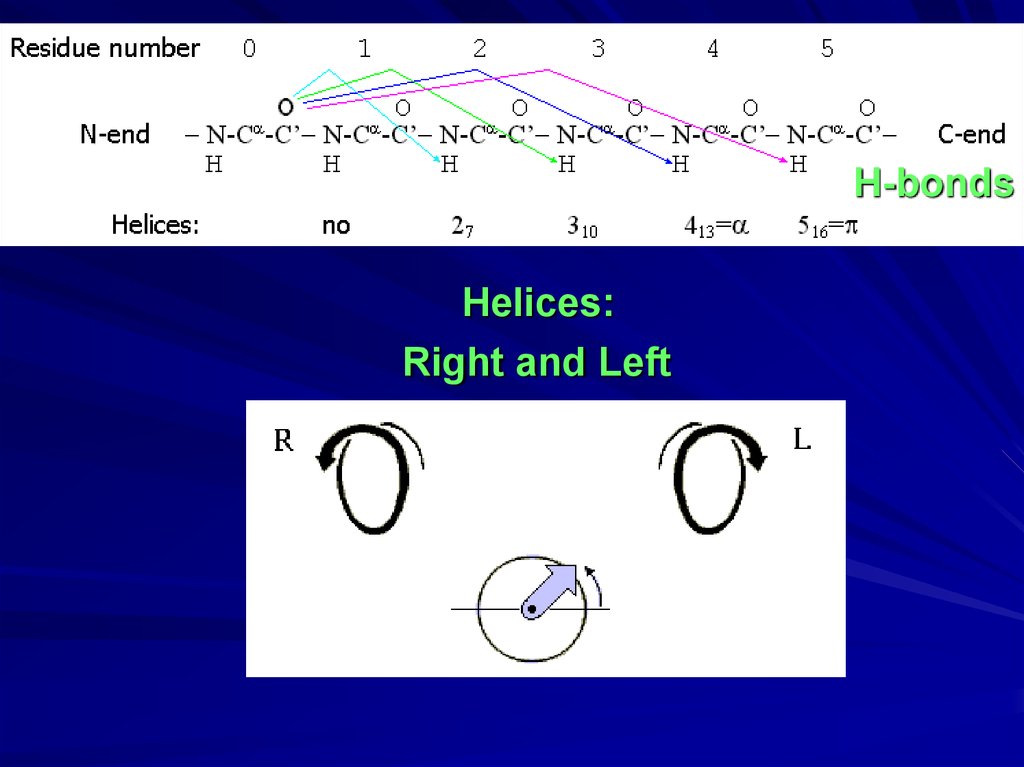
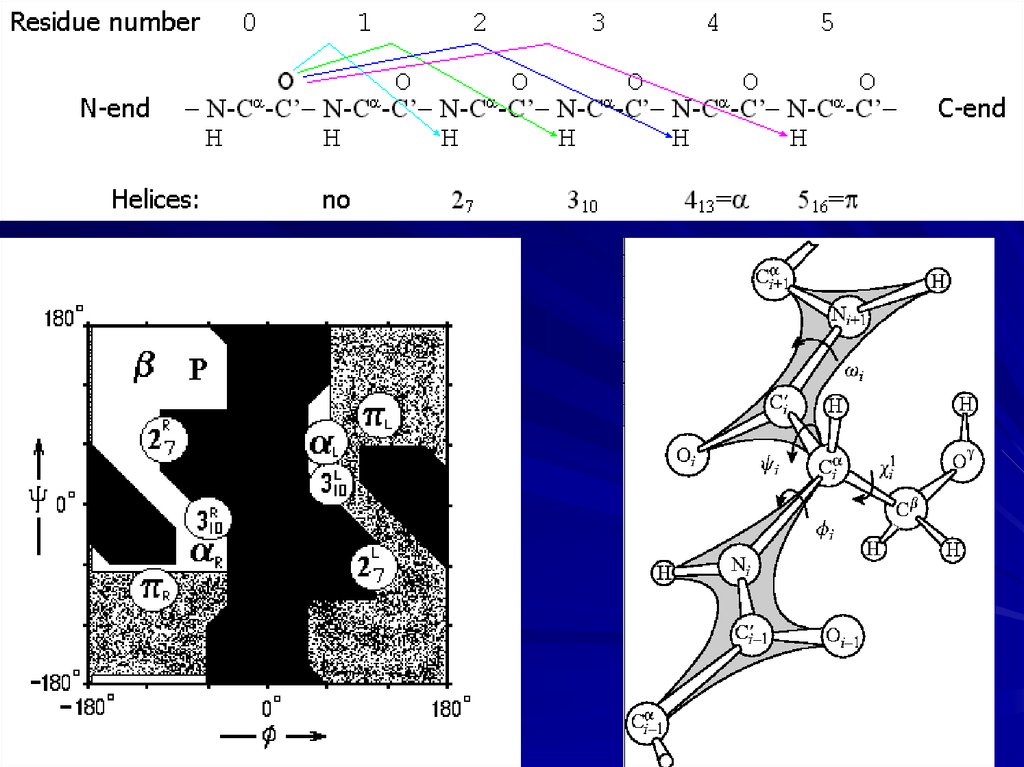
H-bondsHelices:
Right and Left
8.
Right-helix
Right
310-helix
9.
10.
ALA, etc.GLY only
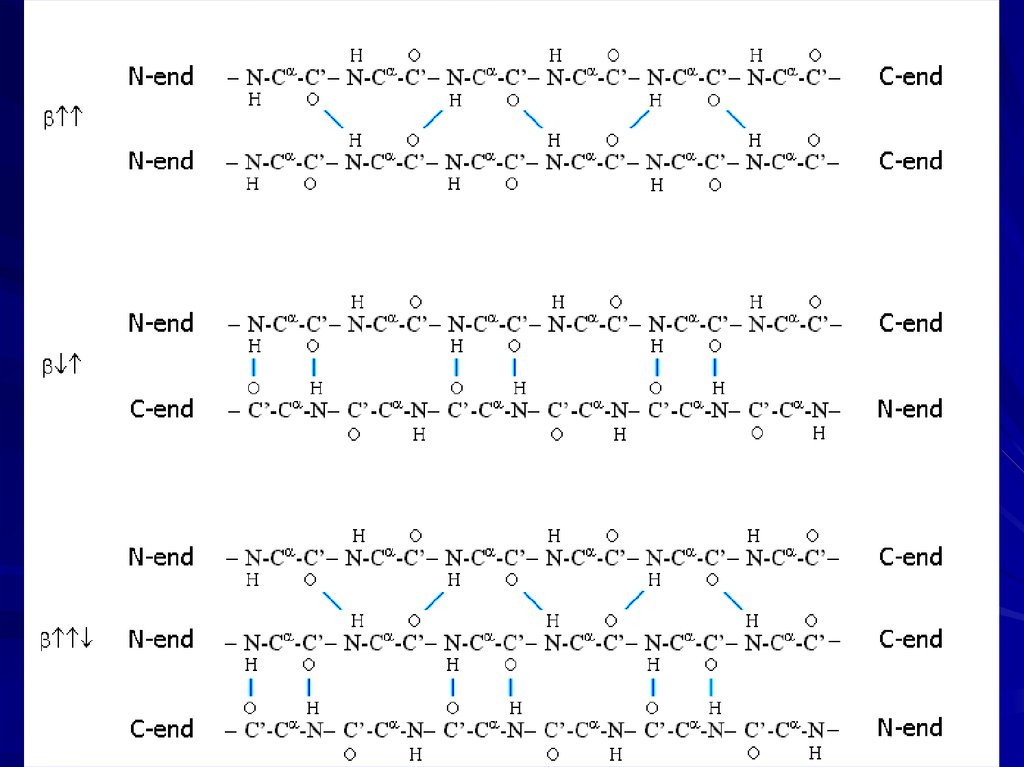
11.
12.
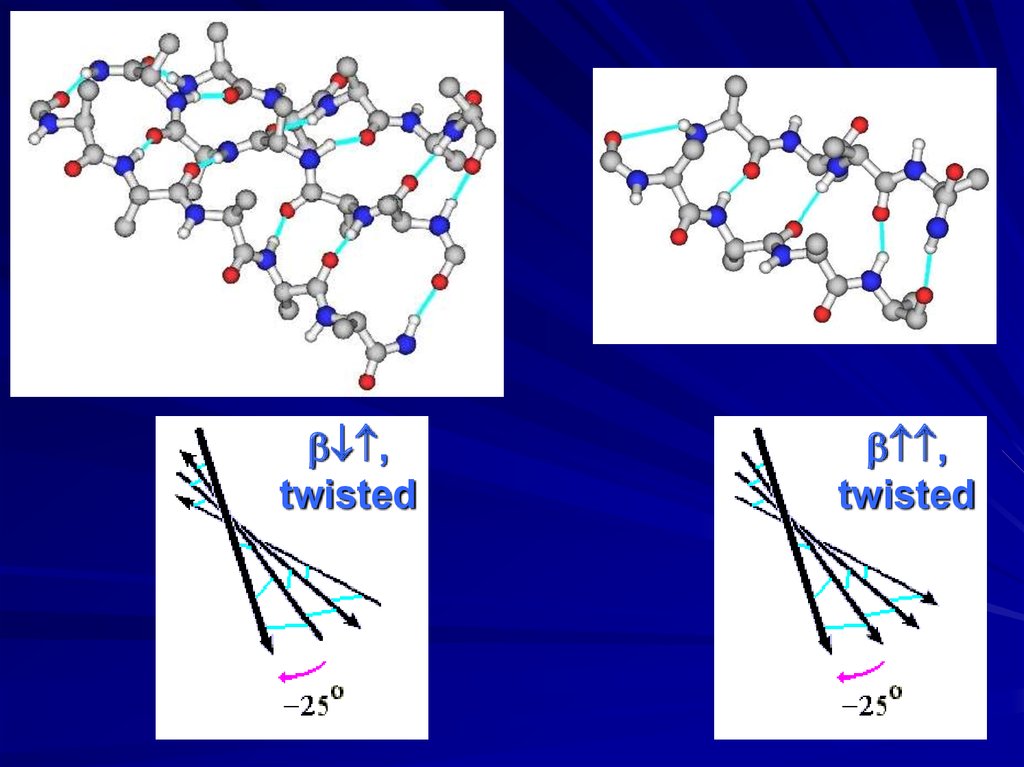
,twisted
,
twisted
13.
Mirror-asymmetricamino acids –
mirror-asymmetric
twist of -sheets
14.
-turns-bulge
15.
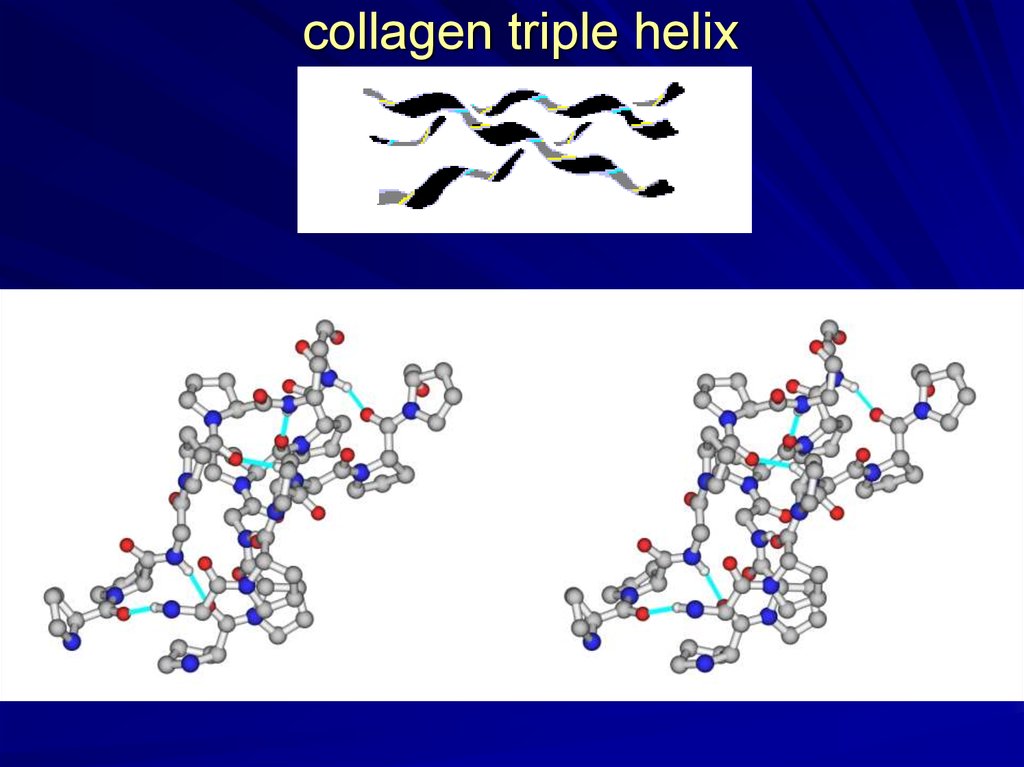
collagen triple helix16.
Secondary structure transitionsSeparation of potential energy
in classic (non-quantum) mechanics:
E = ECOORD + EKIN;
S = SCOORD + SKIN
EKIN=Σmv2/2 - does not depend on coordinates
We may consider
only potential energy, etc.:
E ECOORD
M MCOORD
S(E) SCOORD(ECOORD )
F(E) FCOORD , etc.
17.
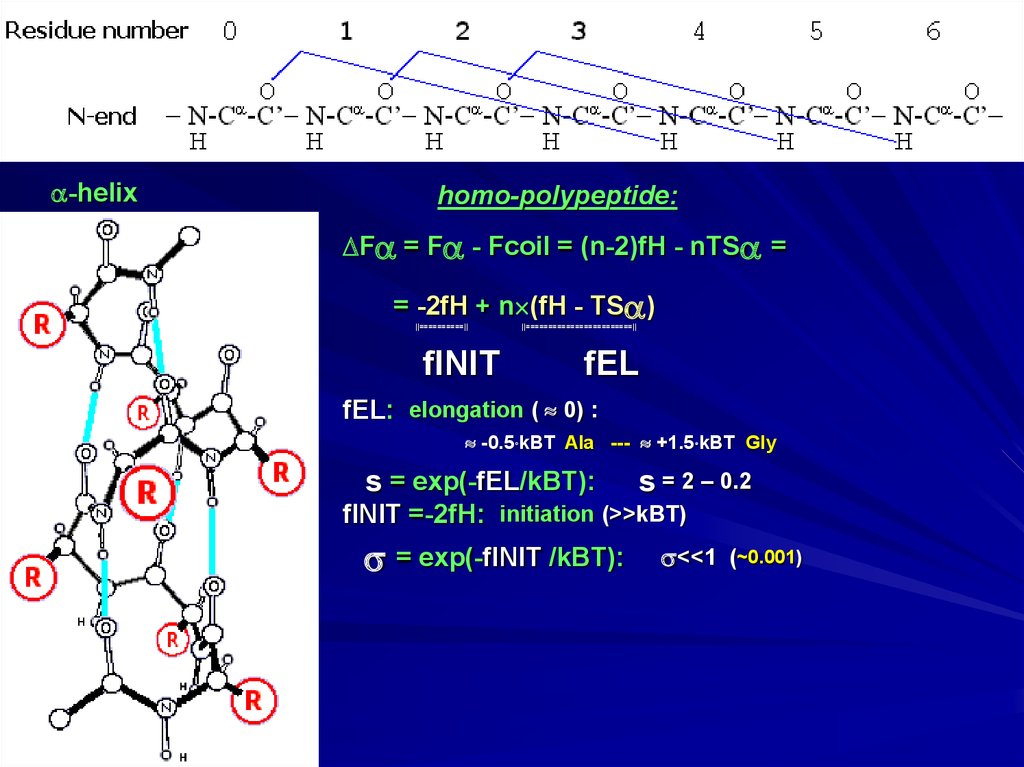
-helixhomo-polypeptide:
F = F - Fcoil = (n-2)fH - nTS =
= -2fH + n (fH - TS )
||==========||
||========================||
fINIT
fEL
fEL: elongation ( 0) :
-0.5 kBT Ala --- +1.5 kBT Gly
s = exp(-fEL/kBT):
s = 2 – 0.2
fINIT =-2fH: initiation (>>kBT)
= exp(-fINIT/kBT):
<<1 (~0.001)
18.
-helixhomo-polypeptide:
F = F - Fcoil = (n-2)fH - nTS =
= -2fH + n (fH - TS )
||==========||
fINIT
||========================||
fEL
fEL: elongation ( 0) :
-0.5 kBT Ala --- +1.5 kBT Gly
s = exp(-fEL/kBT):
s = 2 – 0.2
fINIT =-2fH: initiation (>>kBT)
= exp(-fINIT /kBT):
<<1 (~0.001)
19.
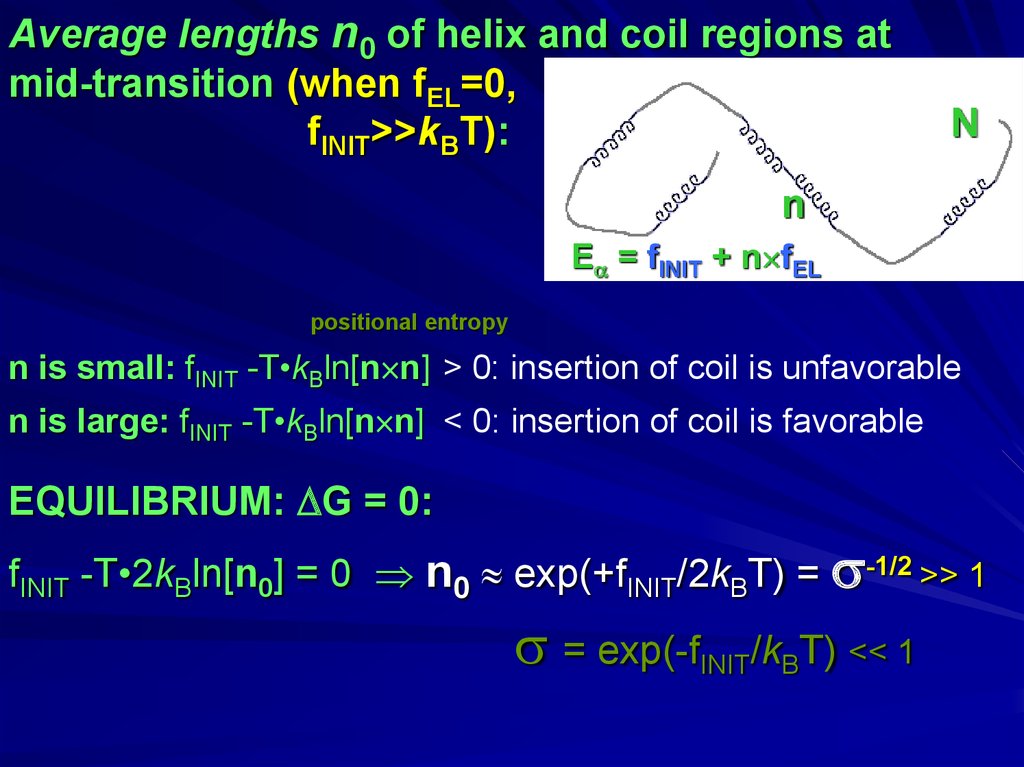
Average lengths n0 of helix and coil regions atmid-transition (when fEL=0,
fINIT>>kBT):
N
n
E = fINIT + n fEL
positional entropy
n is small: fINIT -T•kBln[n n] > 0: insertion of coil is unfavorable
n is large: fINIT -T•kBln[n n] < 0: insertion of coil is favorable
EQUILIBRIUM: G = 0:
fINIT -T•2kBln[n0] = 0 n0 exp(+fINIT/2kBT) = -1/2 >> 1
= exp(-fINIT/kBT) << 1
20.
Widthof helix-coil transition
~n0
~n0
When fEL changes:
IF n0 fEL << - kBT, i.e., fEL/kBT << - 1/n0: stable helix
IF n0 fEL >> +kBT; i.e., fEL/kBT >> + 1/n0: unstable helix,
stable coil
Transition width: [ fEL/kBT ] ~ 4/n0 = 4 1/2
n0 -1/2 30
fEL=0 if % =50%
for very long chain
n0: % 0
when chain is
shorter than n0
21.
TIME of coil-helix transitionBarrier for initiation:
n0 = -1/2
~n0
F# = fINIT;
Time to initiate helix in given place:
t1 = exp(+ F#/kBT) = -1= n02
~ 1–10 ns
Time to initiate helix in any of n0 places:
tINIT_H = n0-1 t1 = n0 -1/2 ~100 ns
To extend helix to n0 residues:
t
= n -1/2 ~100 ns
EL_H
0
tHELIX ~ 200 ns
/
22.
TIME of coil – stable -hairpin transitionfTURN
Barrier for initiation:
F# = fTURN fINIT_ ;
1
Time to initiate -hairpin
n
with turn in the middle of the chain:
t1 exp(+ F#/kBT) = n02 ~ 3000 ns
Time to extend -hairpin to n residues:
tEL_ -HAIRPIN n ~ 100 ns
t -HAIRPIN ~ 3000 ns
/
23.
TIME of coil – -sheet transition (when hairpin is unstable)fTURN
f
fEDGE+f
f < 0
H-phil.:
f = -0.3 – +0.3 kBT;
fEDGE+f > 0
H-phob.: f -1 – -0.5 kBT
F#
f N + fTURN < 0
Nmin = fTURN/(-f )
F# = fTURN +2Nmin(fEDGE+f ) + fTURN = 2 fTURN fEDGE /(-f )
24.
TIME of coil – -sheet transitionF# = 2 fTURN fEDGE /(-f )
when (-f ) 0
Time to initiate -sheet folding:
f < 0
t1 = exp(+ F#/kBT)
!!
fEDGE >-f
when (-f ) 0
Fopt(M#) = 2 fTURN fEDGE /(-f ) - fTURN
fTURN
f
fEDGE+f
F#
25. The End
26.
Average lengths n0 of helix and coil regions atmid-transition (when fEL=0):
# of ends: ; region’s n N/
n
: /2 helices, 1+ /2 coils
E = fINIT + n fEL
N
n
when fEL=0: E = E( +2) - E( ) = fINIT
S( )/kB = ln[N•…•(N- +1) / •…•1];
S/kB = [S( +2) - S( )]/kB 2ln[N/ ] =2ln(n) (when N>> )
EQUILIBRIUM: G = E-T S=0:
fINIT -T•2kBln[n0] = 0 n0 exp(+fINIT/2kBT) = -1/2
(when
<<1)
















 physics
physics








