Геометричні перетворення

1. Геометричні перетворення

Презентацію створив:
Бойко Ростислав

2. Історична довідка

Теорія геометричних перетворень виникла у зв’язку з пізнанням
аконів зображення предметів на площині. Спроби правильно
відобразити на плоскому рисунку природні форми предметів
здійснювалися задовго до виникнення писемності – люди малювали
на стінах печер, скелях, посуді різноманітні рослини, тварин тощо.
Тривала практика підказувала митцям, як передати на рисунку
зображуваний предмет - так зароджувалося вчення про відповідності
й перетворення. Раніше за інші були встановлені й вивчені закони
перспективи. Стародавні греки дотримувалися їх уже в V-IVст.до н.е.
В Епоху Відродження з’явилися перші фундаментальні дослідження
з теорії перспективи, зокрема роботи видатних художників Леонардо
да Вінчі і Альбрехта Дюрера. Розробником математичних основ теорії
проективних перетворень став французький інженер і архітектор
Жерар Дезарг

3.

Завдяки теорії перспективи вдалося досягнути достатньої наочності
зображень, однак технічний прогрес вимагав точного відтворення
об’єктів із дотриманням розмірів. Багато талановитих учених доклали
зусиль до створення теорії взаємно однозначних відповідностей на
площині й у просторі. Серед них був, зокрема, французький
математик Мішель Шаль (1793- 1880), який довів фундаментальну
теорему про геометричні перетворення (нині відому як теорема
Шаля). Підсумував наукові пошуки в галузі геометричних перетворень
французький геометр Гаспар Монж (1746-1818), створивши новий
розділ геометрії - нарисну геометрію.
Пізніше на основі розподілу геометричних перетворень на групи
було виділено ще декілька розділів геометрії – афінна, проективна та
інші. Здобутки вчених у вивченні перетворень склали математичну
основу розвитку багатьох галузей сучасної техніки.

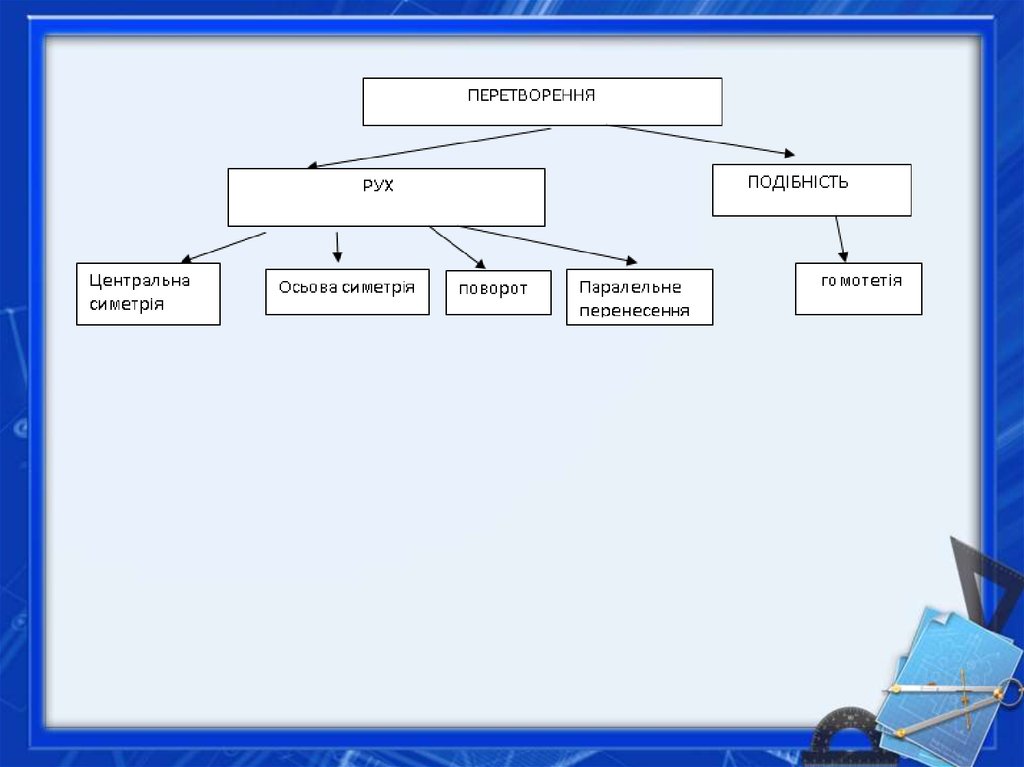
4. Означення

• 1. Перетворенням фігури F у фігуру F1 називається така відповідність,
при якій:
• 1) кожній точці фігури F відповідає єдина точка фігури F1;
• 2) кожній точці фігури F1 відповідає деяка точка фігури F;
• 3) різним точкам фігури F відповідають різні точки фігури F1.
Центральна симетрія
Осьова симетрія

5.

• 2.Переміщенням(або рухом) називається перетворення фігури ,
внаслідок якого зберігаються відстані між точками даної фігури.
• 3.Точки Х і Х1 називаються симетричними відносно точки О, якщо
точка О – середина відрізка ХХ1.
• 4. Точки Х і Х1 називаються симетричними відносно прямої l , якщо ця
пряма перпендикулярна до відрізка ХХ1 і проходить через його
середину.
• 5. Поворотом фігури F навколо точки О на кут F у фігуру F1, унаслідок
якого кожна точка Х фігури F переходить у точку Х1 фігури F1 так, що
ОХ1=ОХ і =

6.

6.Паралельним перенесенням фігури F у напрямі променя ОА на відстань
а називається перетворення фігури F у фігуру F1 , унаслідок якого кожна
точка Х фігури F переходить у точку Х1 фігури F1 так, що промені ХХ1 і ОА
співнапрямлені і ХХ1=а
7.Гомотетією з центром О називається таке перетворення фігури F у фігуру
унаслідок якого кожна така точка Х фігури F переходить у точку Х1 фігури
так що точка Х1 лежить на промені ОХ і ОХ1= kОХ (k- фіксоване додатне
число).
F 1,
F 1,