Геометричні перетворення

1.

2. Переміщення

Працюючи з пластиліном, ми можемо з
однієї фігурки виліпити іншу в результаті
перетворення.
А в геометрії?
Z
Y
Z1
Y1
X точкуXпівкола
1
Кожну
змістили так, що
отримали відрізок. Говорять, що півколо
відобразилося на відрізок.
Відрізок утворився з півкола у
результаті геометричного перетворення.

3. Поняття переміщення

На малюнку перетворення, при якому фігура F відображається на фігуру
F′, особливе. Воно зберігає відстань між відповідними точками фігур.
Будь-які дві точки Х і Y фігури F переходять у точки Х′ і Y′ фігури F′ так,
що ХY = Х′Y′.
Таке перетворення є переміщенням.

4. Переміщення

Перетворення, при якому фігура F
відображається на фігуру F` і зберігає
відстань між відповідними точками
фігур називається переміщенням.
Перетворення називається
переміщенням, якщо воно
зберігає відстань між точками.
05:42

5. До уваги!

Приклад. Деякеперетворення коло переводить у коло (мал. 1).
Чиє цеперетвореняпереміщенням?
Ні, бовоно не зберігаєвідстаньміжвідповіднимиточками: ОХ ≠ О′Х′.
Мал. 1

6. Теорема (властивість переміщення)

При переміщенні
точки, що лежать на
прямій, переходять у
точки, що лежать на
прямій, і зберігається
порядок їх взаємного
розміщення.
Доведення. Нехай три точки А, В, С лежать на
одній прямій.
Тоді одна з них лежить між двома іншими.
Нехай, наприклад, В лежить між А і С.
Тоді АС = АВ+ВС. (1)
Деяке переміщення переводить точки А, В, С у
точки А', В', С'. Оскільки переміщення зберігає
відстані, то АС = А'С', АВ = А'В' і ВС = В'С'. З
цих рівностей і рівності (1) випливає:
А'С'=А'В'+В'С'.
Остання рівність означає, що точки А', В', С'
лежать на одній прямій, а точка В' лежить між
точками А' і С'.

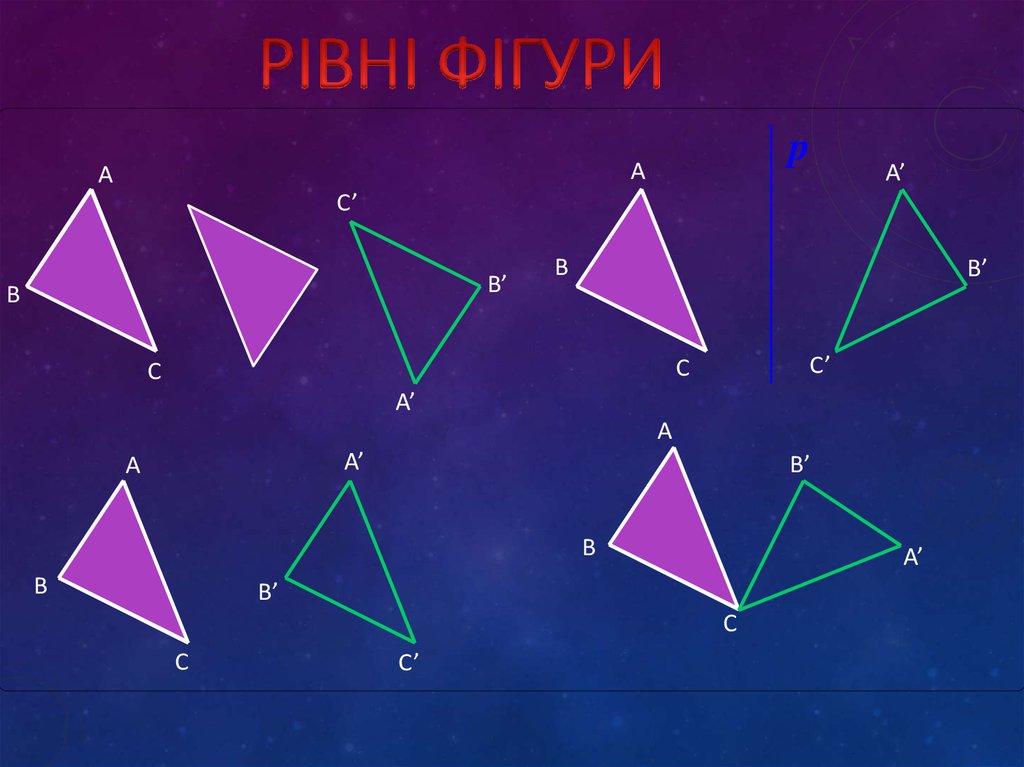
7. Рівні фігури

Узагалі переміщення будь-яку
фігуру переводить у рівну їй
фігуру.
Тому поняття «рівні фігури»
можна визначити за допомогою
поняття «переміщення».
Дві фігури називаються рівними,
якщо вони переводяться
переміщенням одна в одну.

8. Рівні фігури

p
A
A
A’
C’
O
B’
B
B
B’
C’
C
C
A’
A
A’
A
B’
B
B
A’
B’
C
C
C’

9.

Сорока Аліна
Гавриленко Ангеліна
Ільїчова ксенія
Батрак Ельвіра
Чубук Дар’я