Similar presentations:
Перетворення Фiгур. Рух. 9 клас
1.
Урок геометрії в 9 класі2.
3.
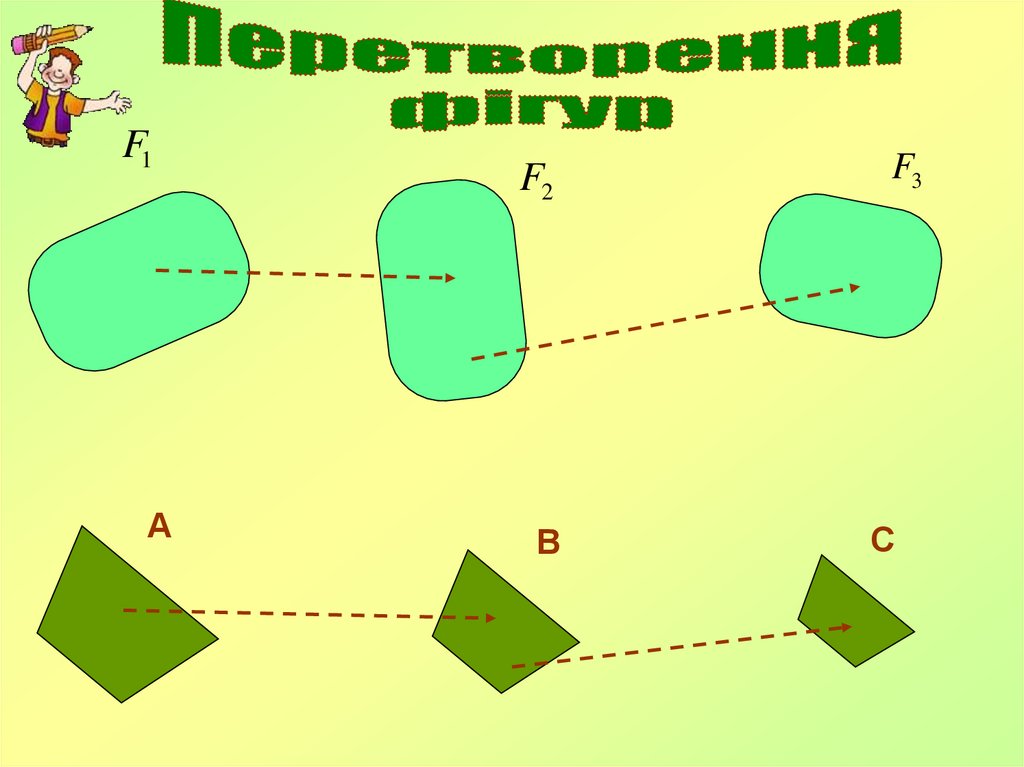
F1А
F2
В
F3
С
4.
ОЗН. Перетворення однієї фігури в їншу, при якомузберігається відстань між точками, називається рухом.
5.
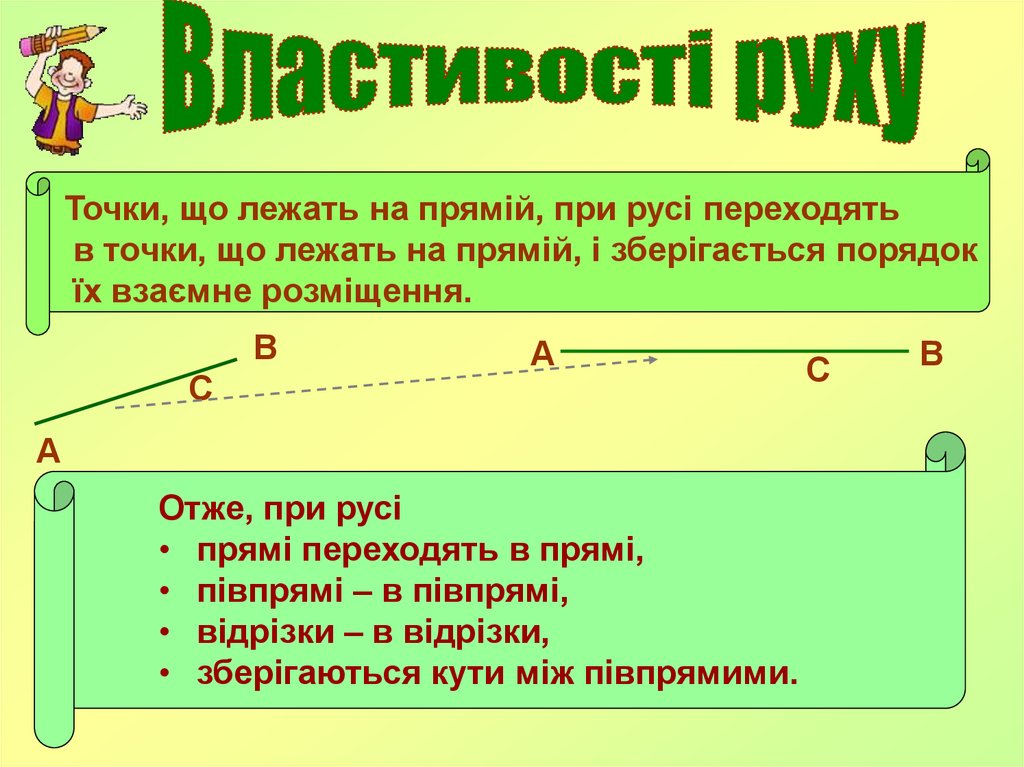
Точки, що лежать на прямій, при русі переходятьв точки, що лежать на прямій, і зберігається порядок
їх взаємне розміщення.
В
С
А
А
Отже, при русі
• прямі переходять в прямі,
• півпрямі – в півпрямі,
• відрізки – в відрізки,
• зберігаються кути між півпрямими.
С
В
6.
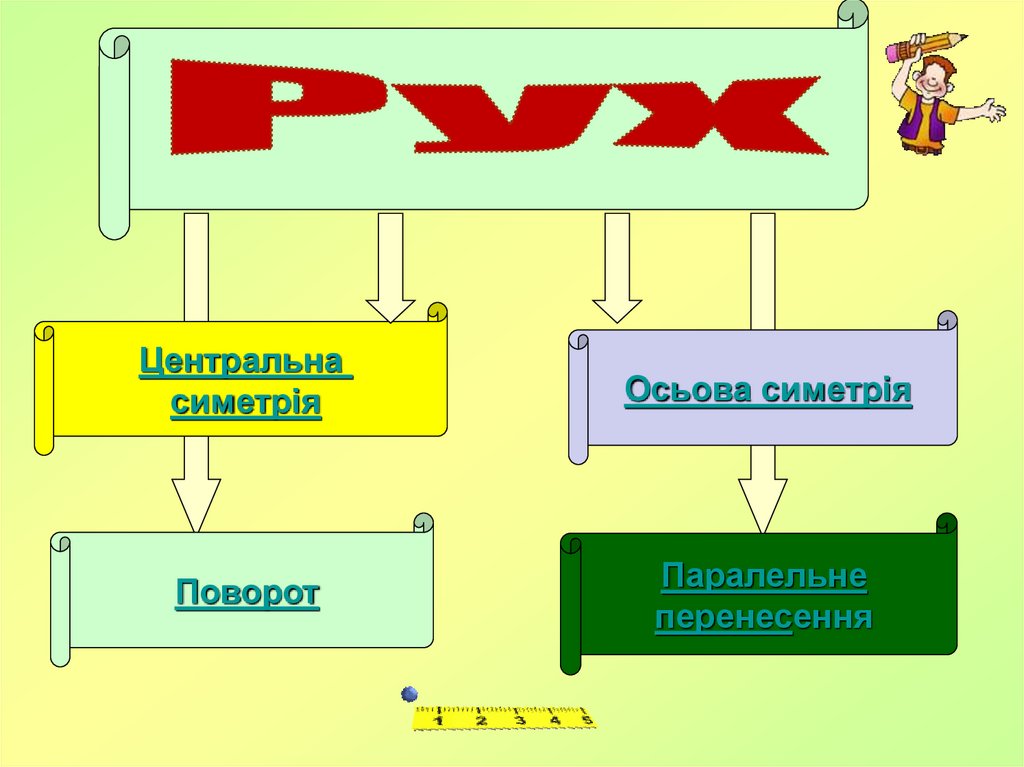
Центральнасиметрія
Осьова симетрія
Поворот
Паралельне
перенесення
7.
АО
В
X
О
Y1
Y
X1
Точка А симетрична точці В відносно
центра симетрії – точки О
8.
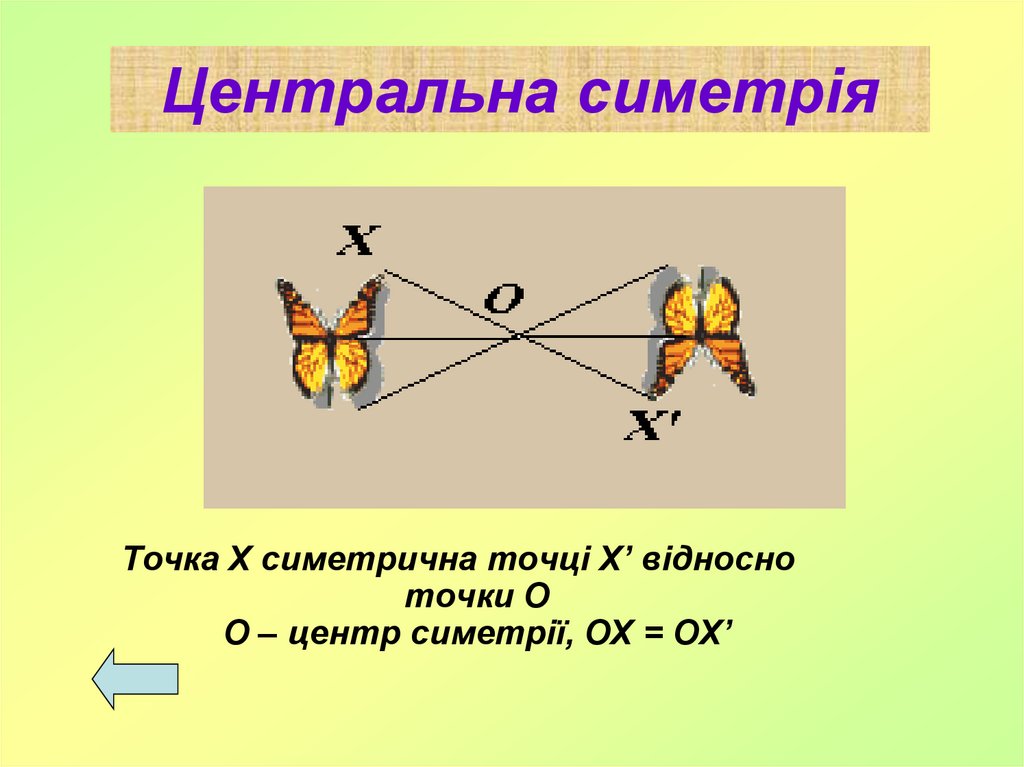
9. Центральна симетрія
Точка Х симетрична точці X’ відносноточки О
О – центр симетрії, ОХ = ОX’
10.
11.
12.
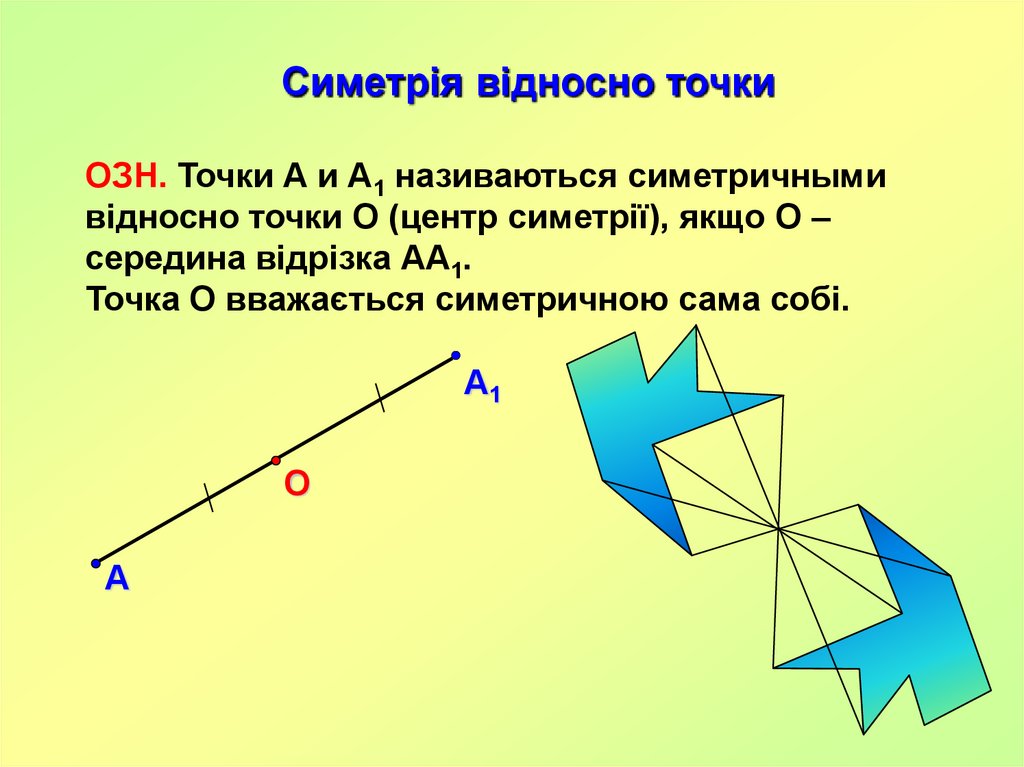
Симетрія відносно точкиОЗН. Точки А и А1 називаються симетричными
відносно точки О (центр симетрії), якщо О –
середина відрізка АА1.
Точка О вважається симетричною сама собі.
А1
О
А
13.
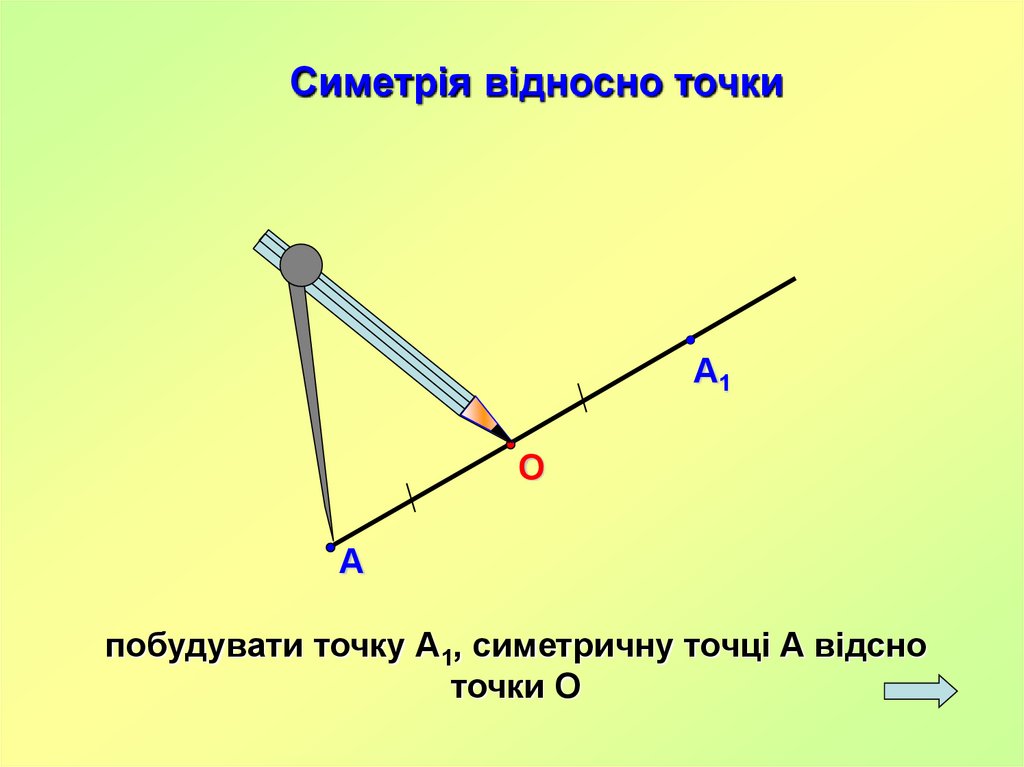
Симетрія відносно точкиА1
О
А
побудувати точку А1, симетричну точці А відсно
точки О
14.
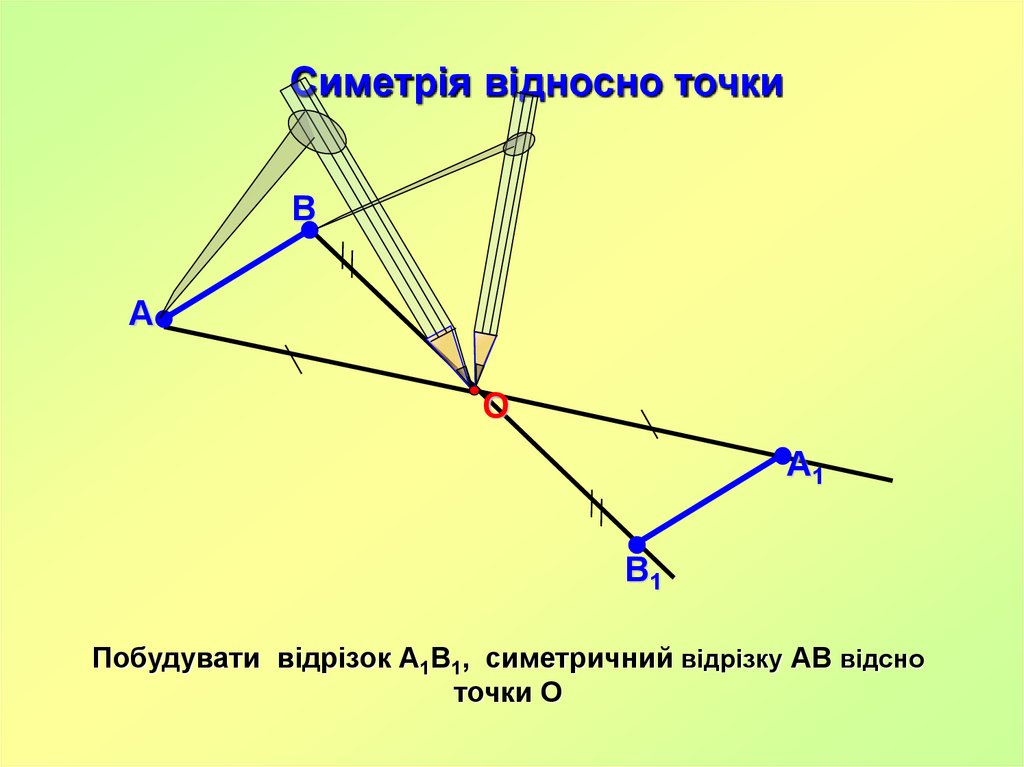
Симетрія відносно точкиВ
А
О
А1
В1
Побудувати відрізок А1В1, симетричний відрізку АВ відсно
точки О
15.
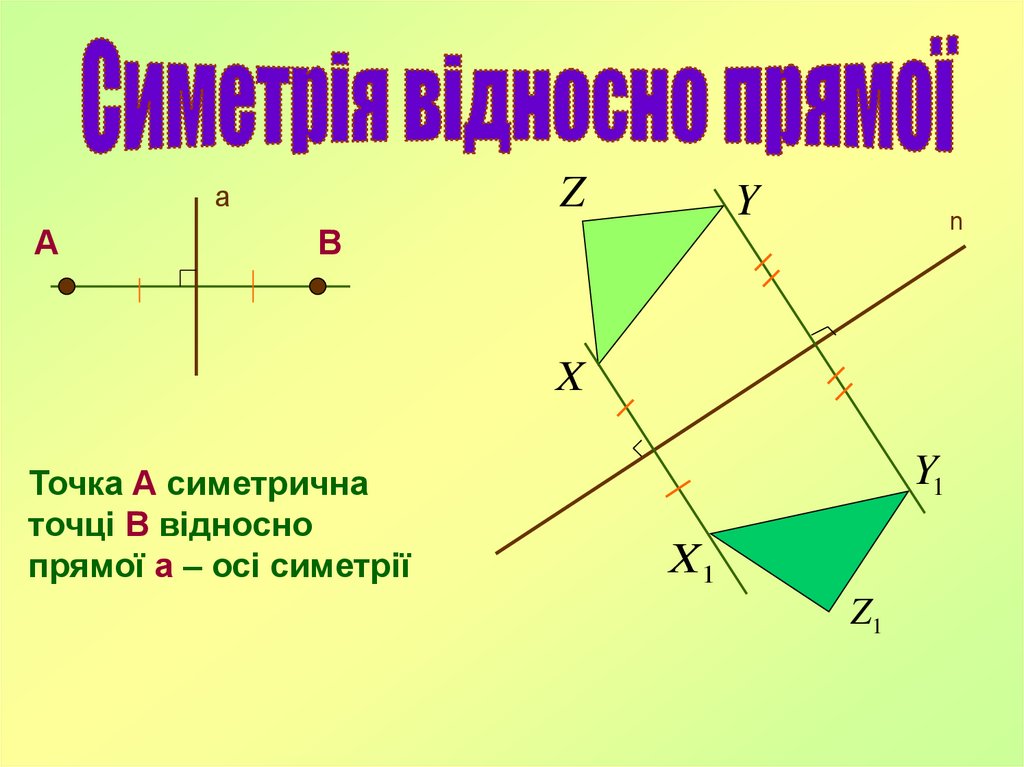
Zа
А
Y
В
n
X
Точка А симетрична
точці В відносно
прямої а – осі симетрії
Y1
X1
Z1
16.
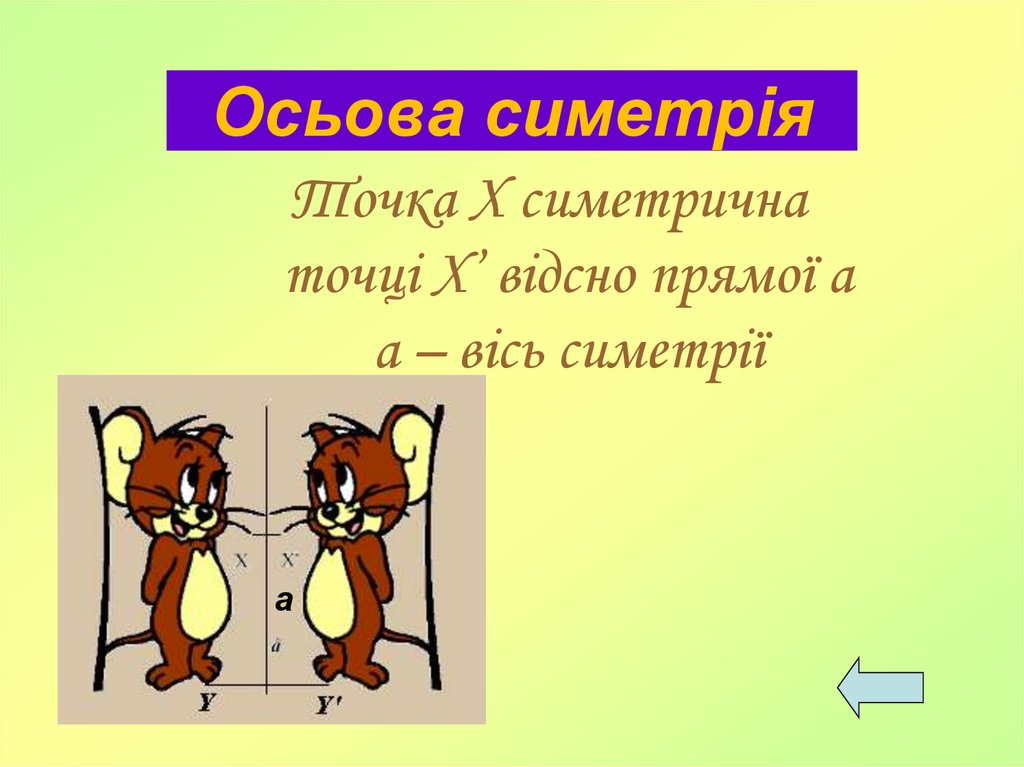
17. Осьова симетрія
Точка Х симетричнаточці X’ відсно прямої а
а – вісь симетрії
a
18.
19.
20.
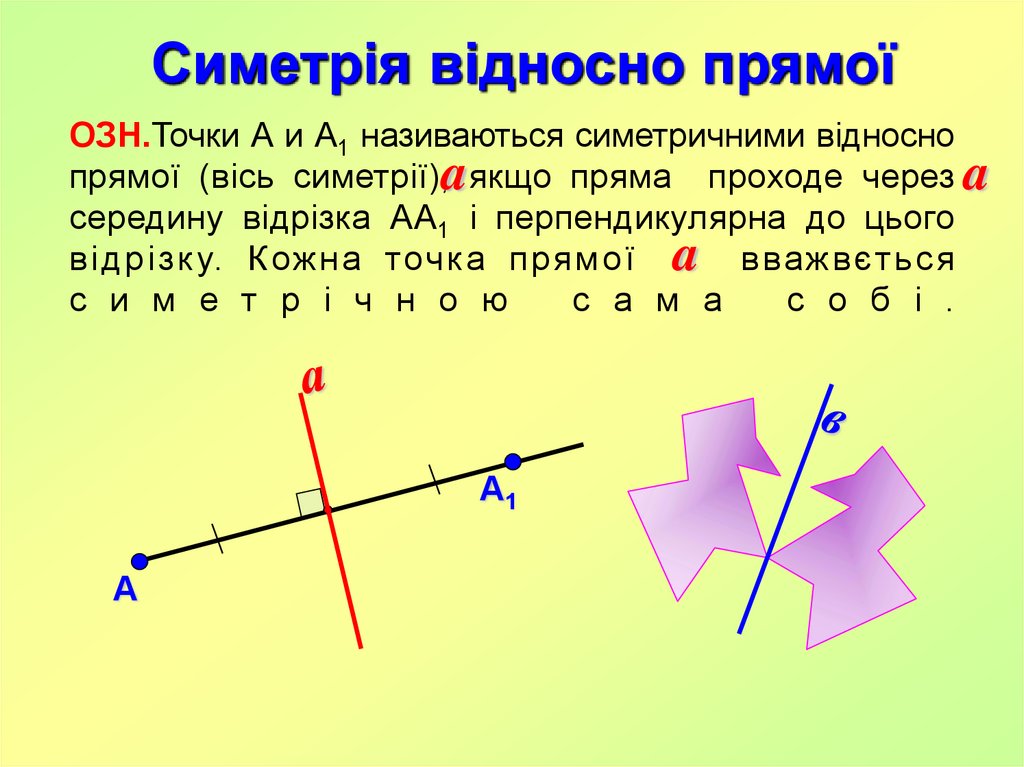
Симетрія відносно прямоїОЗН.Точки А и А1 називаються симетричними відносно
прямої (вісь симетрії),a якщо пряма проходе через a
середину відрізка АА1 і перпендикулярна до цього
від р із к у. К ож на точк а прям о ї a вважвєт ьс я
с и м е т р і ч н о ю
с а м а
с о б і .
А1
А
21.
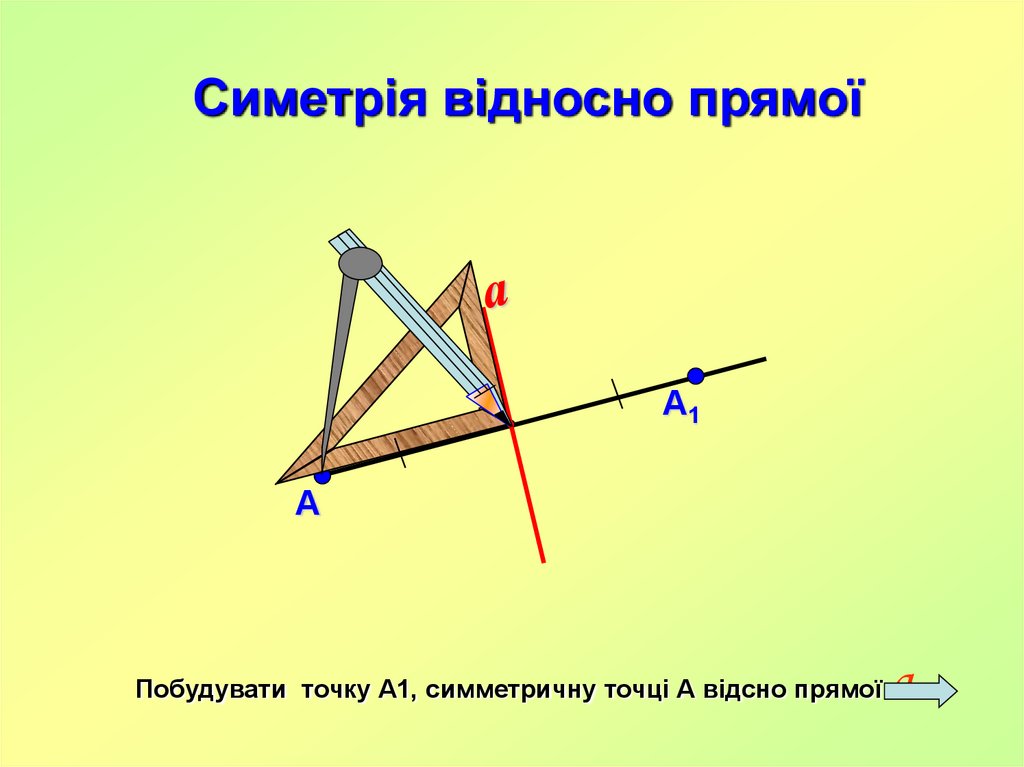
Симетрія відносно прямоїА1
А
Побудувати точку А1, симметричну точці А відсно прямої
а
22.
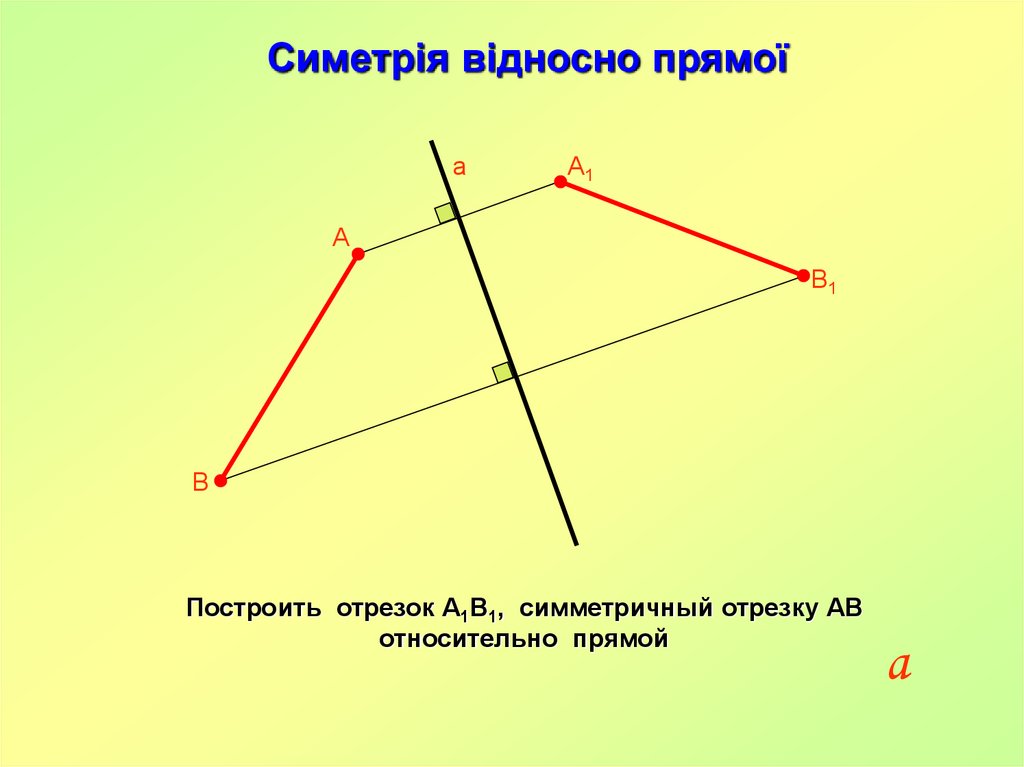
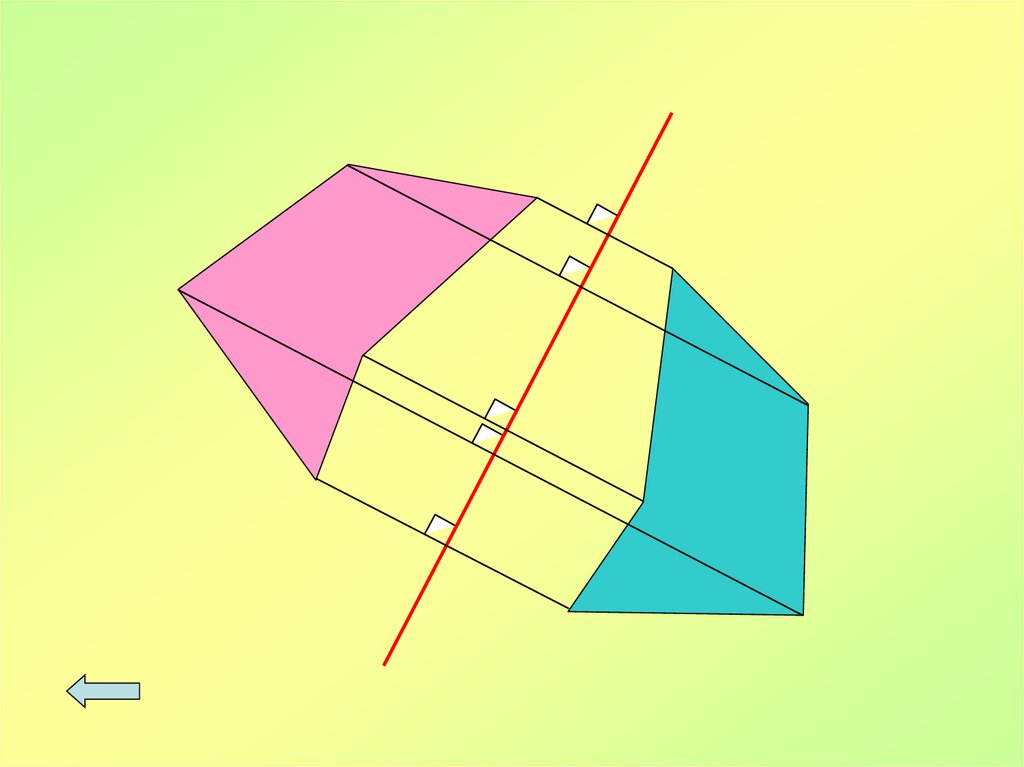
Симетрія відносно прямоїа
А1
А
В1
В
Построить отрезок А1В1, симметричный отрезку АВ
относительно прямой
а
23.
24.
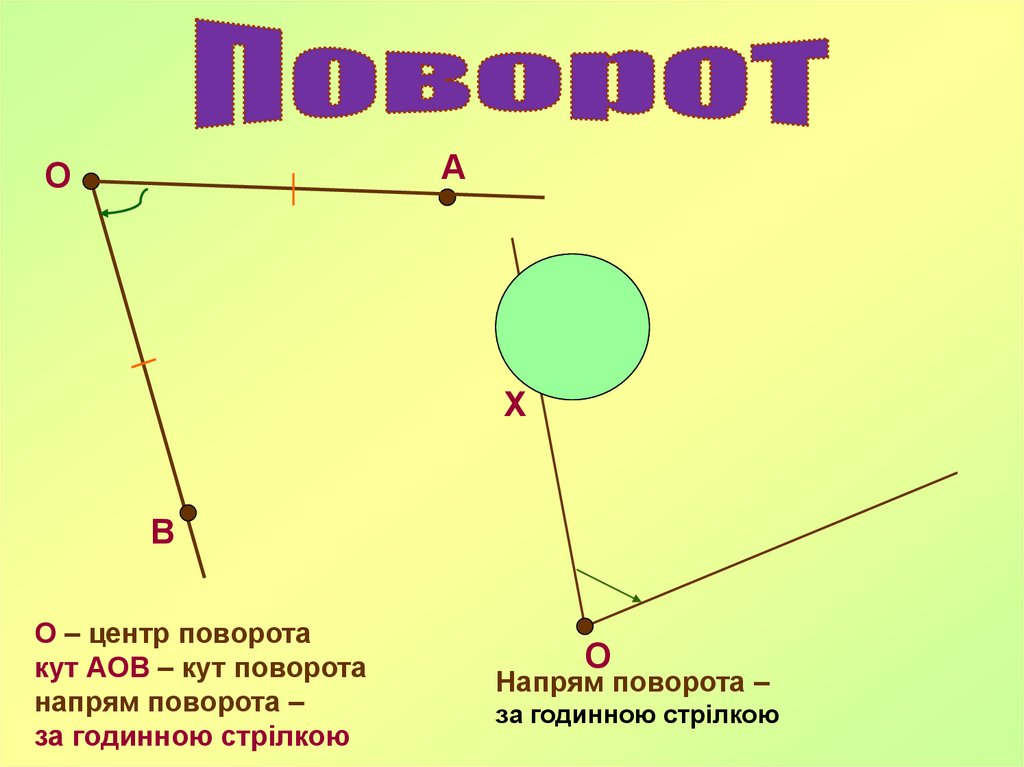
АО
Х
В
О – центр поворота
кут АОВ – кут поворота
напрям поворота –
за годинною стрілкою
О
Напрям поворота –
за годинною стрілкою
25.
26. Поворот
Точка Х переходе в точкуХ’
а – кут поворота
27.
ОЗН. Перетворення фігури F, при якому її довільна точка(х; у) переходить в точку (х+а; у+в) називається
паралельним перенесенням.
Паралельне перенесення задається формулами:
x x a ,
y y b
28.
Приклад. Паралельне перенесення задаєтьсяформулами x x 2,
y y 3
В які точки при цьому
паралельному
перенесенні переходять точки
О(0;0), А(0;4), В(-4;1)?
О О (2; 3)
А А ( 2;1)
В В ( 2; 2)
у
5
4
3
2
1
В
О
А
А
х
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
В
О
29.
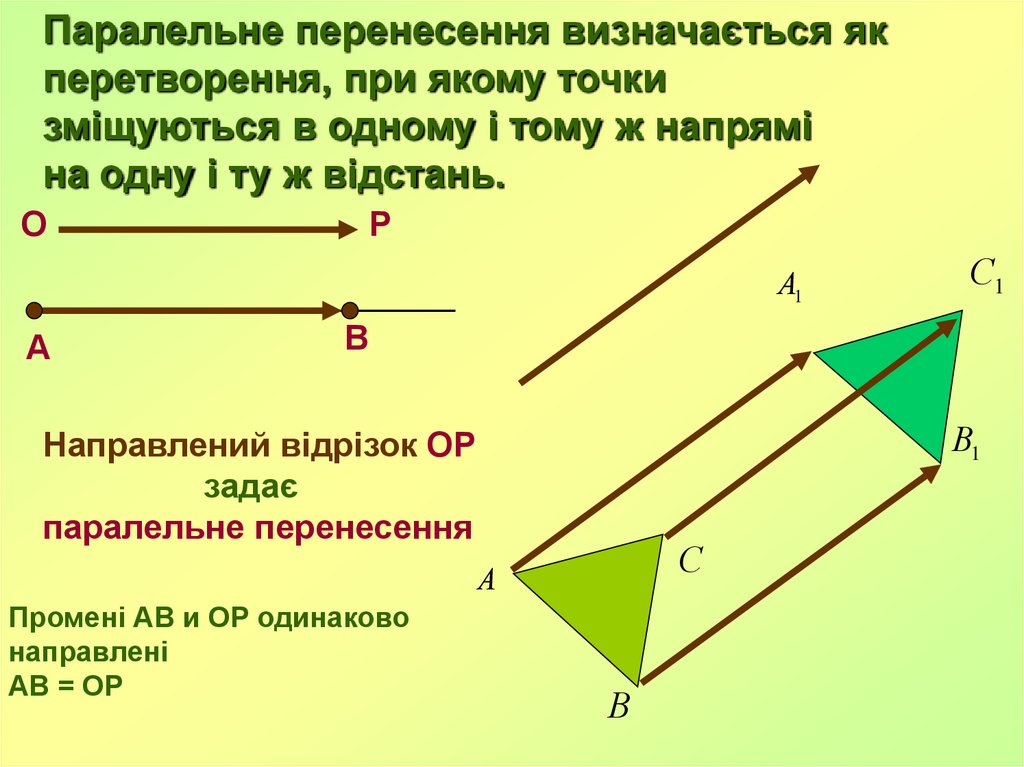
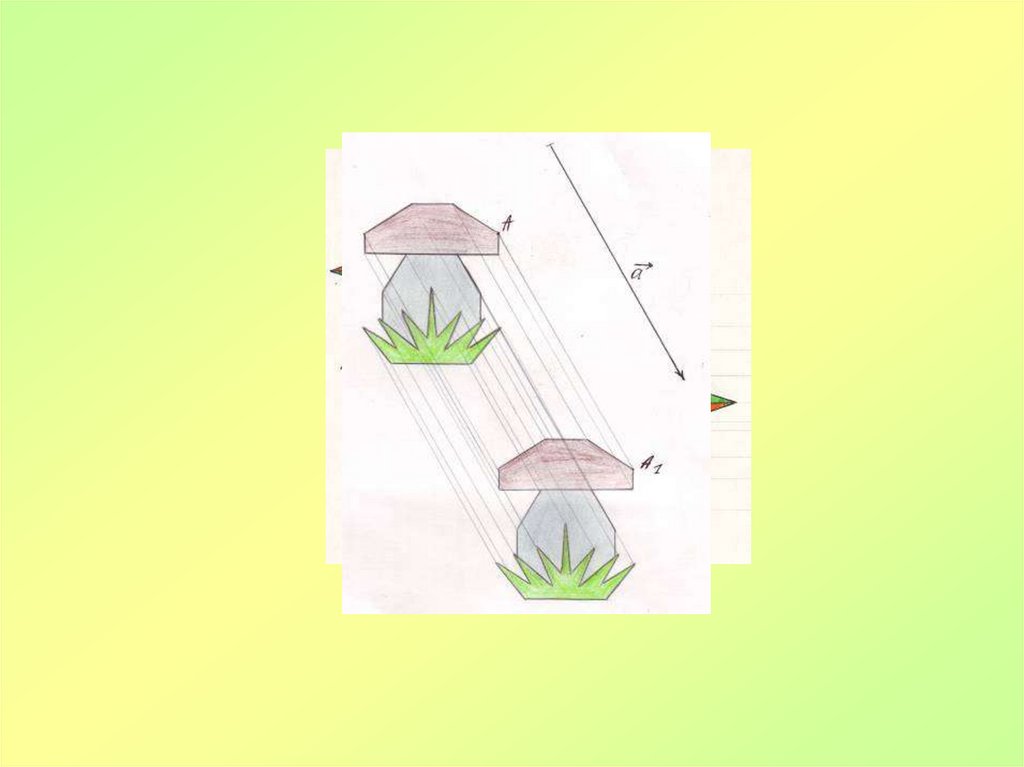
Паралельне перенесення визначається якперетворення, при якому точки
зміщуються в одному і тому ж напрямі
на одну і ту ж відстань.
О
Р
А1
А
С1
В
В1
Направлений відрізок ОР
задає
паралельне перенесення
С
А
Промені АВ и ОР одинаково
направлені
АВ = ОР
В
30.
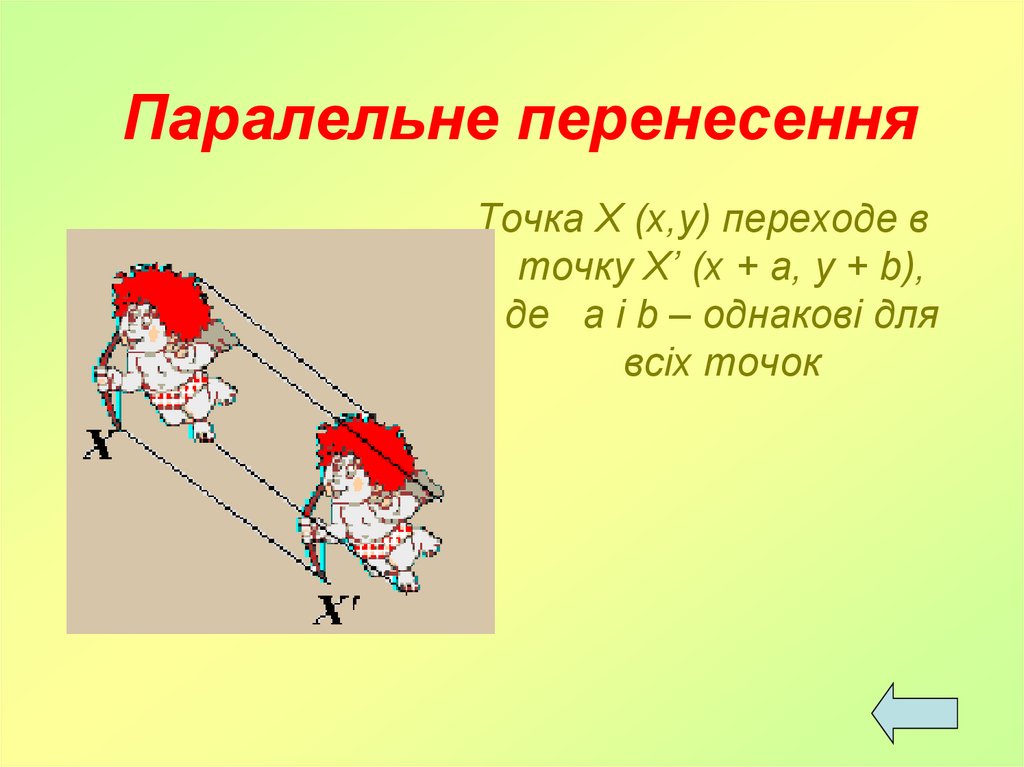
31. Паралельне перенесення
Точка Х (х,у) переходе вточку Х’ (x + a, y + b),
де a і b – однакові для
всіх точок
32.
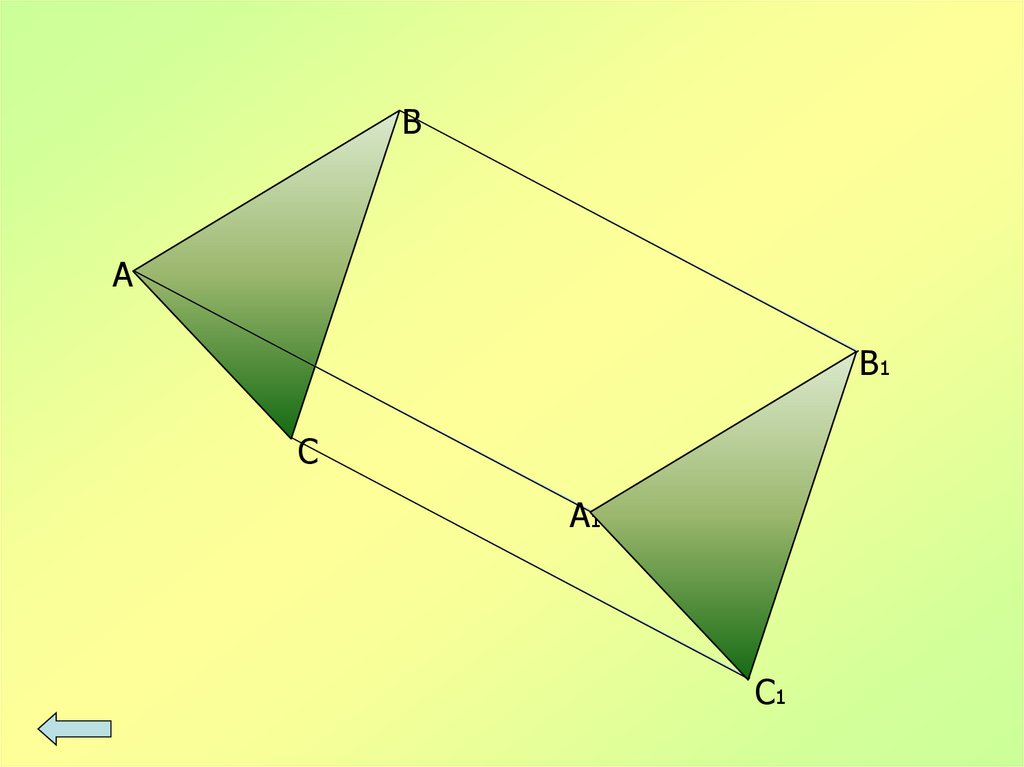
ВА
В1
С
А1
С1









 mathematics
mathematics








