Наиболее эффективный способ отбора корней тригонометрического уравнения

1. ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ Тема: «О наиболее эффективном способе отбора корней тригонометрического уравнения».

IX ЕЖЕГОДНЫЙ ВСЕРОССИЙСКИЙ КОНКУРС ДОСТИЖЕНИЙ ТАЛАНТЛИВОЙ МОЛОДЁЖИ
«НАЦИОНАЛЬНОЕ ДОСТОЯНИЕ РОССИИ»
ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ
Тема: «О наиболее эффективном
способе отбора корней
тригонометрического уравнения».
Подготовила ученица 10 класса МБОУ
« СШ №25» п. Энем Республики Адыгея
Карпенко Виктория.
Руководитель проекта Ведерникова И.А.

2. АКТУАЛЬНОСТЬ

3.

Содержание:
1.Теория
2.
Исследование
Уметь выбирать необходимое;
Цель:
Расширить кругозор
учащихся;
Тема:
Наиболее
эффектив
ный
способ
отбора
корней
тригоном
етрическ
ого
уравнени
я
Делать вывод и использовать
научиться
выбирать
корни
тригономет
рических
уравнений
из
заданного
промежутка
разными
способами;
определить
наиболее
оптимальн
ый метод
отбора
корней с
наименьше
й затратой
времени;
ВВЕДЕНИЕ
полученные сведения
Создать базу данных;
Результат:
Существует ли
такой способ
отбора корней
тригонометрическ
их уравнений,
который с
наименьшей
затратой времени
даст решение.
3.Вывод
4. База заданий
5.Список
литературы
Найден
наиболее
эффективн
ый способ
отбора
корней
тригономе
трического
уравнения

4. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Разложение на
множители
Формулы сокращенного
умножения
Группировка
Основные методы решения
тригонометрических
уравнений
Вынесение за скобки
f(x).р(x)=0
Введение новой
переменной
Однородное ур-ние
первой степени
Деление обеих частей на
cos x
sin x=a
cos x=a,
Однородное ур-ние
второй степени
1. Если есть asin2x, то деление
на cos2x с последующим
введением новой переменной
2. Если нет asin2x, то метод
разложения на множители
tg x=a,
ctg x=a.
Решение квадратного уравнения

5. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

sin x=a ,
Простейшие
тригонометрические
уравнения
cos x=a,
tg x=a,
ctg x=a.

6. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

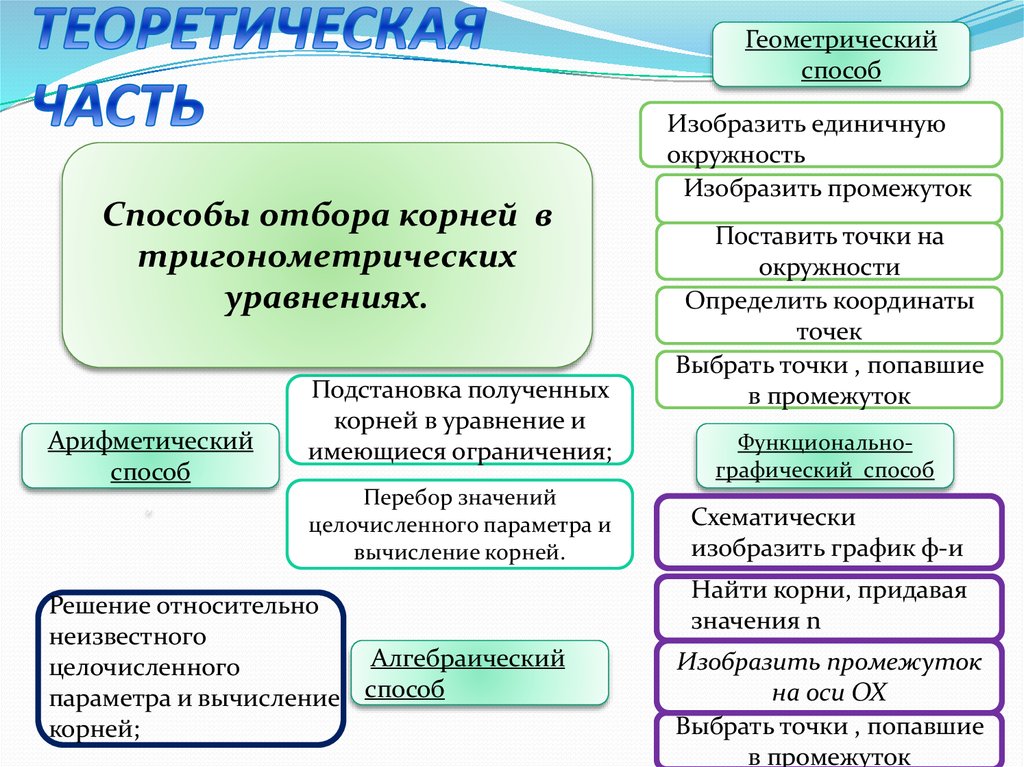
Геометрический
способ
Способы отбора корней в
тригонометрических
уравнениях.
Арифметический
способ
,
Подстановка полученных
корней в уравнение и
имеющиеся ограничения;
Перебор значений
целочисленного параметра и
вычисление корней.
Решение относительно
неизвестного
Алгебраический
целочисленного
параметра и вычисление способ
корней;
Изобразить единичную
окружность
Изобразить промежуток
Поставить точки на
окружности
Определить координаты
точек
Выбрать точки , попавшие
в промежуток
Функциональнографический способ
Схематически
изобразить график ф-и
Найти корни, придавая
значения n
Изобразить промежуток
на оси ОХ
Выбрать точки , попавшие
в промежуток

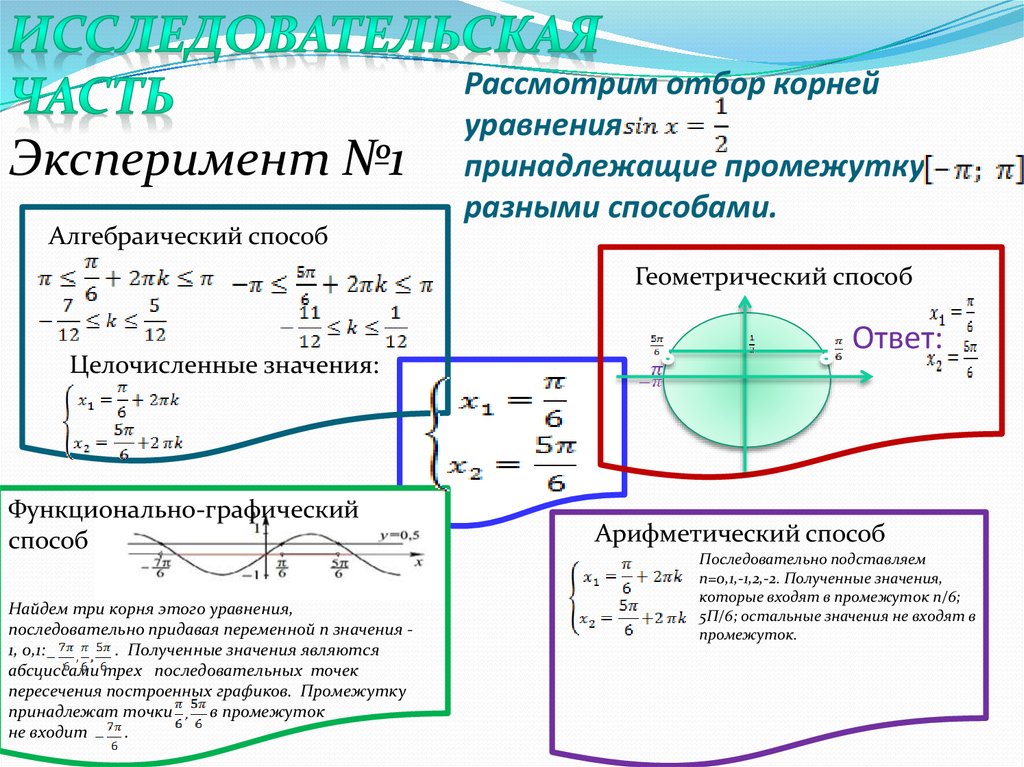
7. Рассмотрим отбор корней уравнения принадлежащие промежутку разными способами.

Эксперимент №1
Алгебраический способ
Рассмотрим отбор корней
уравнения
принадлежащие промежутку
разными способами.
Геометрический способ
Целочисленные значения:
Функционально-графический
способ
Найдем три корня этого уравнения,
последовательно придавая переменной n значения 1, 0,1:
. Полученные значения являются
абсциссами трех последовательных точек
пересечения построенных графиков. Промежутку
принадлежат точки
в промежуток
не входит
.
Ответ:
Арифметический способ
Последовательно подставляем
n=0,1,-1,2,-2. Полученные значения,
которые входят в промежуток п/6;
5П/6; остальные значения не входят в
промежуток.

8.

Решение уравнения с табличным значением
Арифметический
Алгебраический Геометрический Функциональнографический
Затруднение с
перебором
6 минут
решено
решено
решено
5 минут
3 минут
6 минут

9. ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ Эксперимент №2

Эксперимент №2
.
Алгебраический способ
2.Рассмотрим уравнение
с не
табличным значением и найдем
корни на промежутке
аналогичными способами.
Функционально-графический способ
Точки пересечения прямой и синусоиды и есть,
искомые корни уравнения .Промежутку
(принадлежат две точки arcsin
и
Арифметический способ
Последовательно подставляем
n=0,1,-1,2,-2. Полученные значения,
которые входят в промежуток arcsin1\3 и
п-arcsin 1\3 ; остальные значения не входят
в промежуток.
Геометрический способ
Ответ:

10.

Решение уравнения с не табличным значением
Арифметический
Алгебраический Геометрический Функциональнографический
Затруднение в
вычислениях
7 минут
Затруднение в
вычислениях
-
решено
решено
4 минуты
6 минут

11.

2
6
sin
x cos x 5 0
6a a 1 0
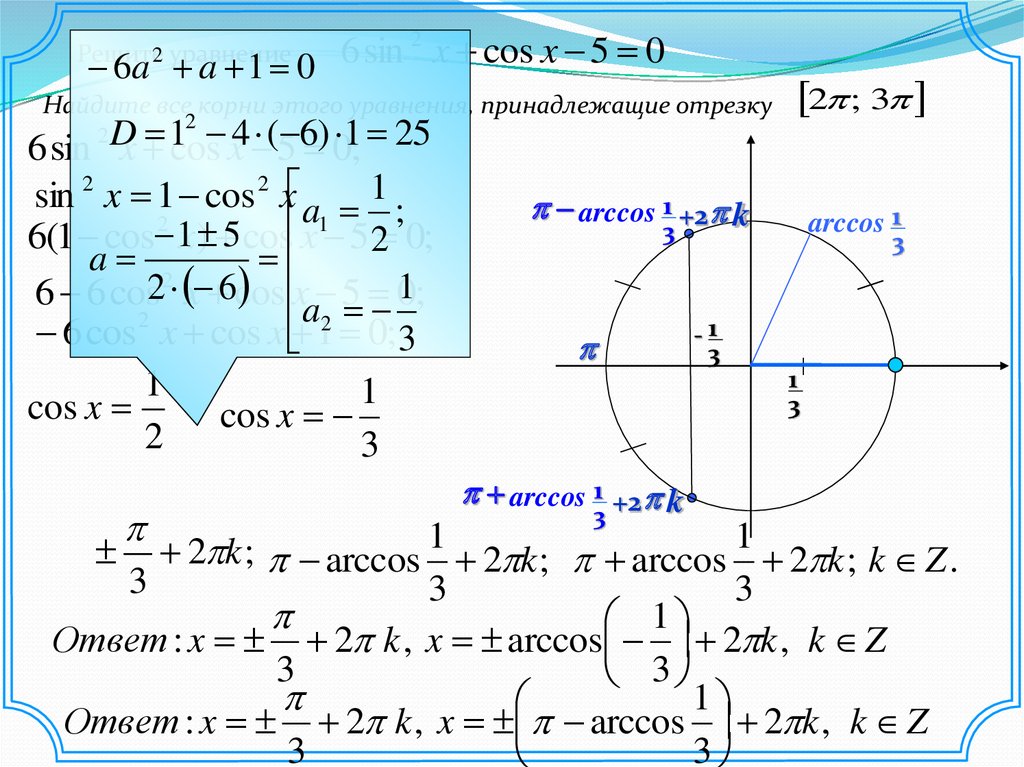
Решите2 уравнение
Найдите все корни этого уравнения, принадлежащие отрезку
1cos x4
(5 6 ) 0 1; 25
6 sin 2Dx
sin 2 x 1 cos 2 x a 1 ;
6(1 cos 2 1x) 5 cos x1 52 0;
a 2
xa 5 01;
6 6 cos2 x 6cos
6 cos 2 x cos x 12 0; 3
1
1
cos x
cos x
2
3
2
2 ; 3
arccos 1 +2 k
arccos 1
3
3
-1
3
1
3
arccos 1 +2 k
3
2 k ; arccos 1 2 k ; arccos 1 2 k ; k Z .
3
3
3
1
Ответ : x 2 k , x arccos 2 k , k Z
3
3
1
Ответ : x 2 k , x arccos 2 k , k Z
3
3

12.

Найдите все корни этого уравнения, принадлежащие отрезку 2 ; 3
1
cos x
3
1
cos x
2
5 7
2 3
3 arccos 1
3
- arccos 1
3
3
+
-1
3
3
2
1 7
Ответ : 3 arccos ;
.
3 3
1
2
3
2
6 7
2
.
3
3 3
3

13. исследовательская часть

14.

15.

Решение уравнения с не табличным значением
1 команда
Алгебраический
+
+
+
+
+
+
+
+
25 минут
2 команда
3 команда
4 команда
Алгебраический Геометрический Геометрический
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
29 минут
+
15 минут
+
17 минут

16.

Цель проекта достигнута
реализованы

17. С помощью нескольких исследований я доказала, что наиболее эффективным и менее затратным по времени является геометрический

способ.

18.

1)diffur.kemsu.ru
2)Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения:
методы решения и отбор корней
3) ЕГЭ 2012. Математика. Типовые тестовые задания под
ред. А.Л. Семенова, И.В. Ященко. – М.: Издательство
«Экзамен», 2012.
4)www.egemathem.ru – единый государственный экзамен
(от А до Я).

19.

Спасибо за внимание!