Решение тригонометрических уравнений. Некоторые способы отбора корней

1. Решение тригонометрических уравнений. Некоторые способы отбора корней

Выполнила:
учитель математики и информатики
Краснослободцева М.П.

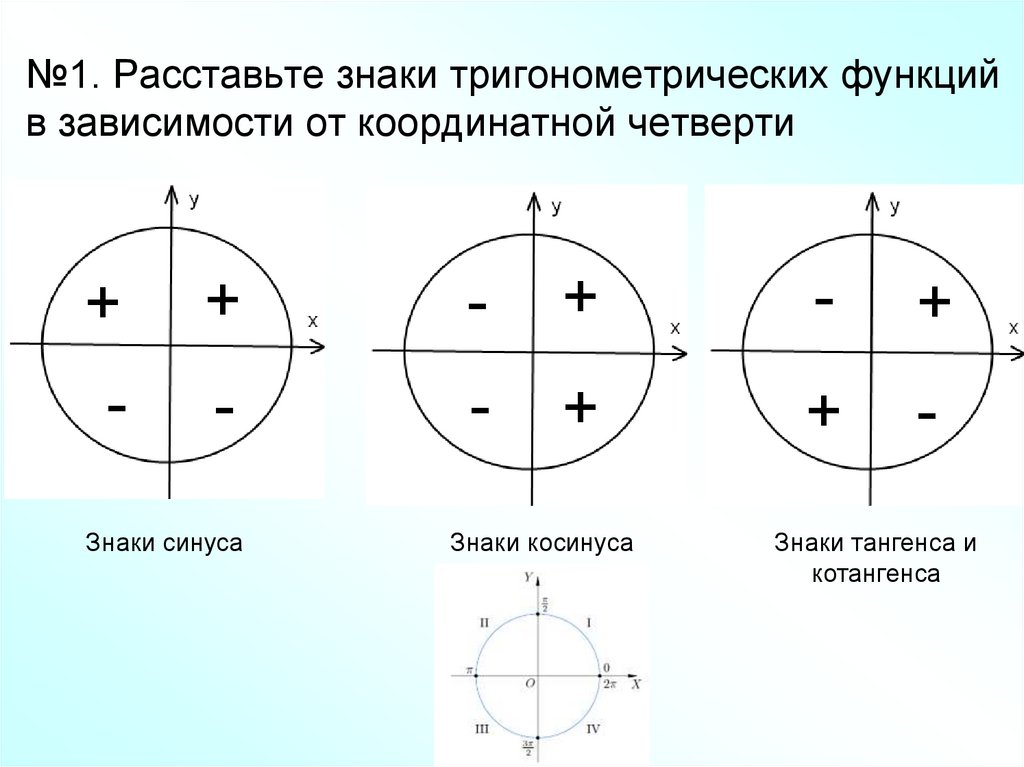
2. №1. Расставьте знаки тригонометрических функций в зависимости от координатной четверти

+
+
-
+
-
+
-
-
-
+
+
-
Знаки синуса
Знаки косинуса
Знаки тангенса и
котангенса

3. №2. Разделите на 2 группы следующие выражения и заполните таблицу:

Функция меняется на
«кофункцию»
Функция не меняется
на «кофункцию»
Выражение
Выражение
Результат
Результат

4.

3
2
cos
2
х
4
sin
х
1 0
а) Решите уравнение
2
2
2
cos 2 x cos x sin x
б) Найдите все корни этого уравнения, принадлежащие отрезку 3 ;
2 cos 2х 4 cos х 1 0
2
2
sin
x
1
cos
2 cos 2 х sin 2 х 4 cos х 1x 0
2 cos 2 х 2 sin 2 x 4 cos х 1 0
2 cos 2 х 2 1 cos 2 х 4 cos х 1 0
По формуле приведения:
«синус» изменится на «косинус»
IVчет.
3
sin x – cos х
2
В IV четв. знак исходной функции
синуса отрицательный
4a 2 4a 3 0
2 cos 2 х 2 2 cos 2 х 4 cos х D
1 042 4 4 ( 3) 64
4 cos 2 х 4 cos х 3 0
Пусть cos x=a, -1≤a≤1
1
2 1
2 2 n
х хarccos
2 n, n Z
3 2
cos х
12
a
4 8 1 8
a
1
2 4
a2
2
а)Ответ : х
1;1
2
2 n, n Z .
3
Т-ца значений

5.

Найдите все корни этого уравнения, принадлежащие отрезку
2
n=-1 x x
2 n
2
3
2 n
3
3 ;
2
3 2n 1
3
2
2
3 2n 1
3
3
11
5
2n
3
3
11
5
n
6
6
n 1,
:
4
x
3
2
3
:2
3 ;
2
2 n
3
3 ;
n=-1
2
3 2n 1 2
3
3
1
1
2 2n
3
3
7
1
:2
2n
3
3
7
1
n
6
6
n 1,
82
3
xx
2 ,
33
:

6.

Отбор корней с помощью графиков
б) Найдите все корни этого уравнения
принадлежащие отрезку 3 ;
,
1
cos x
2
3
- 8
3
5
2
2
y cos x
- 4
3
3
2
y
2
1
x
-1
5 3
15
16
8
.
2 6
6
6
6
3
4
3
9
8
.
3
2 6
6 6
6
3
8
4
б )Ответ : х ; х
.
3
3
Т-ца знач.

7.

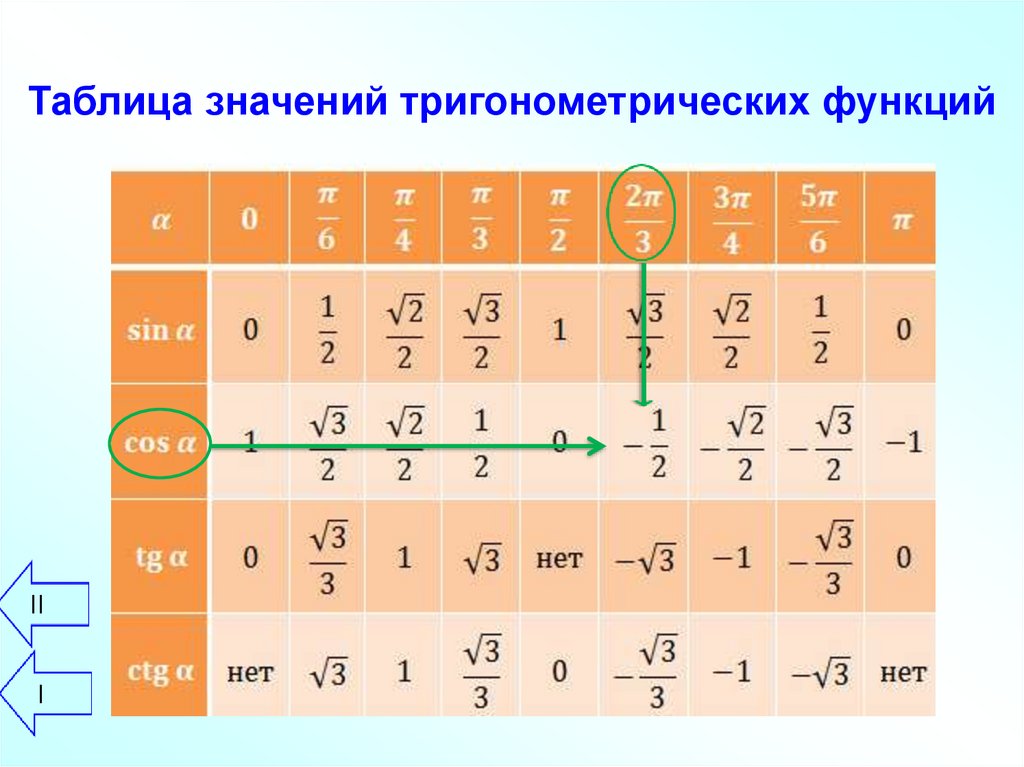
Таблица значений тригонометрических функций
II
I