Отбор корней при решении тригонометрических уравнений

1. Отбор корней при решении тригонометрических уравнений

2.

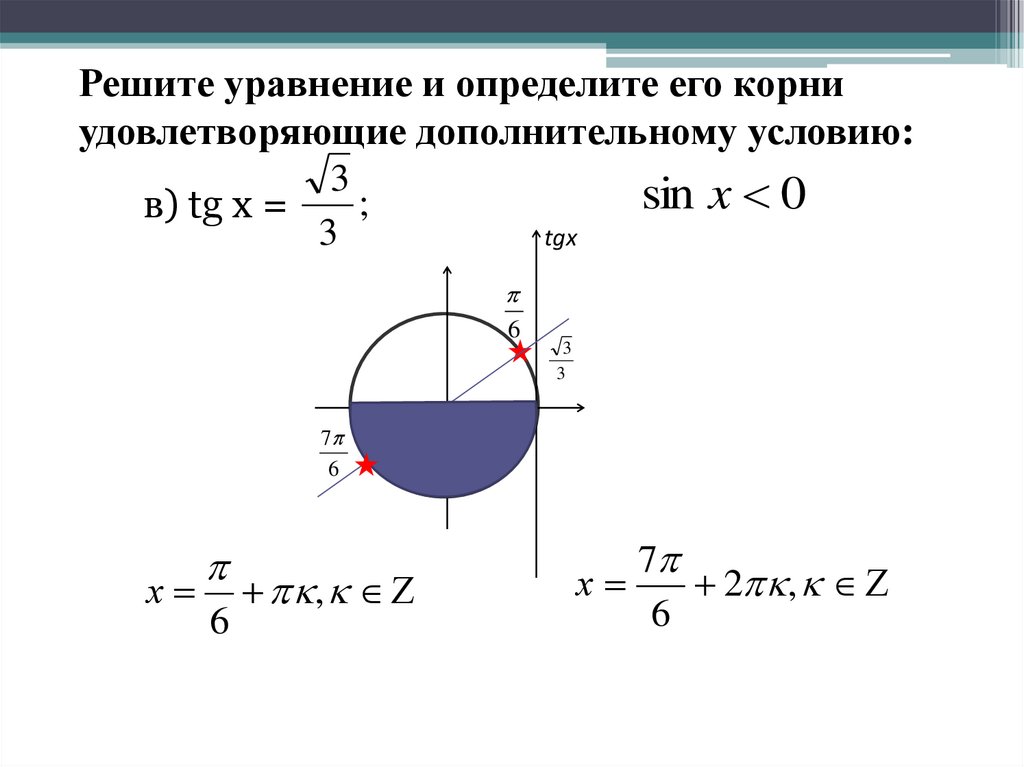
Решите уравнение и определите его корни
удовлетворяющие дополнительному условию:
3 3
x
;
а) cos x = - 1;
3 / 2
2
2
cosx
3 / 2
х 2 ,
х

3.

Решите уравнение и определите его корни
удовлетворяющие дополнительному условию:
cos x 0
б) sin х = 1/2
sinx
5
6
х
2 ,
6
5
х
2 ,
6
6
х
6
2 ,

4.

Решите уравнение и определите его корни
удовлетворяющие дополнительному условию:
3
sin x 0
;
в) tg x =
3
tgx
6
3
3
7
6
х
6
,
7
х
2 ,
6

5.

.
Отбор корней в тригонометрическом уравнении
с помощью числовой окружности
Пример: 1.
а) решите уравнение sin x sin 2x = sin2 x,
5
;
б) определите корни принадлежащие интервалу 2 2
Решение.
sin x sin 2x – sin2 x = 0
sin x 2sinxcosx – sin2 x = 0
2 sin2x cosx – sin2 x = 0
sin2 x (2cosx – 1) = 0
sin2 x = 0 или 2cosx – 1 = 0
sin x = 0
cosx = ½

6.

sin x = 0
x k , k Z
cosx = ½
x
3
5
2
2 k , k Z
3
5
;
2 2
7
3
0
2
0
5
7
;0; ; ; ;2 ;
.
3
3
3
3
2
3
5
3

7.

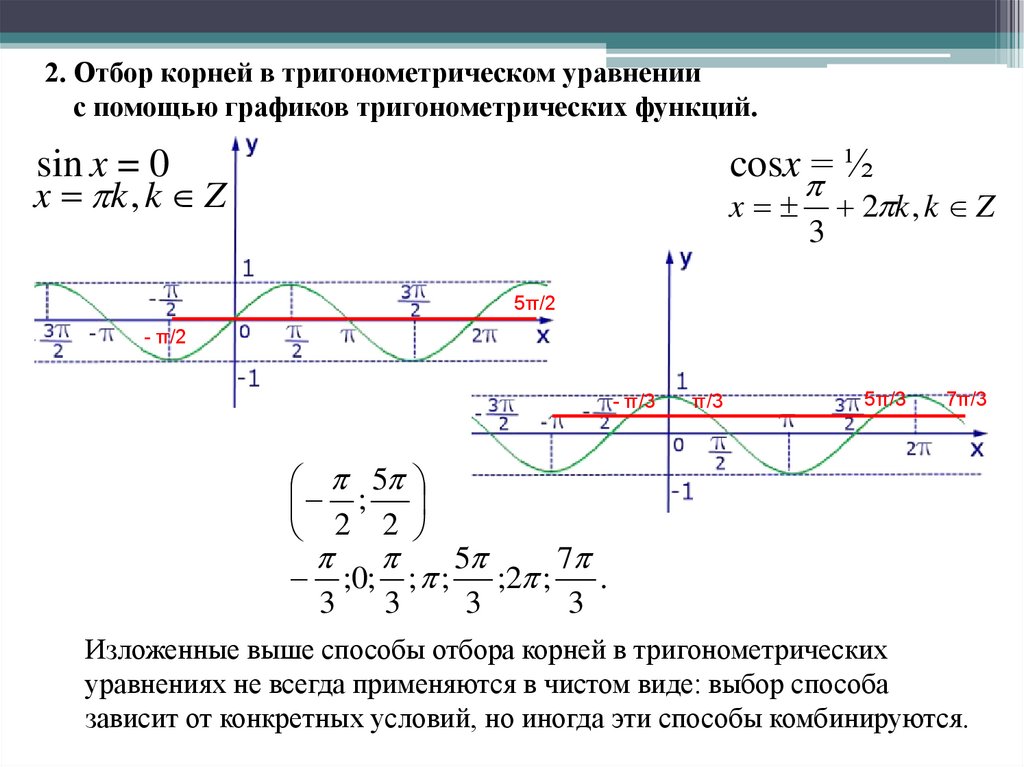
2. Отбор корней в тригонометрическом уравнении
с помощью графиков тригонометрических функций.
cosx = ½
sin x = 0
x k , k Z
x
3
2 k , k Z
5π/2
- π/2
- π/3
π/3
5π/3
7π/3
5
;
2 2
5
7
;0; ; ; ;2 ;
.
3
3
3
3
Изложенные выше способы отбора корней в тригонометрических
уравнениях не всегда применяются в чистом виде: выбор способа
зависит от конкретных условий, но иногда эти способы комбинируются.

8.

Пример 3. Найти все корни уравнения
7
2
10 cos (
2
x) sin(
2
2 x) 3,
которые удовлетворяют условию x [
Решение.
10sin2 x = – cos 2x + 3;
10sin2 x = 2sin2 x – 1 + 3,
8sin2 x = 2;
1
sin 2 x ;
4
1
sin x ;
2
k
x
(
1
)
k , k Z ,
6
x ( 1) m ( ) m, m Z ;
6
y
6
n, n Z ;
2
5
6
6
0
7
6
С помощью числовой окружности получим:
x
2 19
;
].
3 12
x
3
2
6

9.

Выберем с помощью двойного неравенства
корни, удовлетворяющие условию задачи.
Из первой серии: 2 n 19 , n Z ;
3
6
12
8 2 12 n 19 , n Z ;
10 12n 17, n Z .
Следовательно n=0 или n=1, то есть x ,
6
x 7 .
6
2
19
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ;
Из второй серии:
6 12n 21, n Z .
Следовательно n=0 или n=1, то есть x ,
Ответ : {
5 7
;
6 6
;
6
6
x 5 .
6
}.

10.

Работа в парах (по вариантам).
Решите уравнение и определите его корни
принадлежащие интервалу ( - π ; 2π)
1). 6 cos 2 x cos x 1 0
5). sin x cos x 0
2). 3 sin 2 x- sin x 0
6). sin 2 x 2 sin x cos x cos 2 x 2
3). tgx 5ctgx 6
7). sin 2 x 2 sin x cos x 3 cos 2 x
4). 1 cos x cos 2 x 0
8). cos 2 x 3 sin x cos x 0