Similar presentations:
Отбор корней при решении тригонометрических уравнений
1. Отбор корней при решении тригонометрических уравнений
2.
1. Вычислите:а) arcsin(-1) ;
2
3 ;
б) arccos ( )
6
2
(не существует);
в) arcsin 2
г) arctg 3
д) arccos ( )
2
3
;
(не существует);
е) arсctg ( 3 ) arctg
5
3
.
6
3.
2. Решить уравнения:а) cos x = - 1;
х 2 ,
1
б) sin х = ;
2
1
х ( 1) arcsin( ) ,
2
1
k 1
х ( 1) arcsin ,
2
k 1
х ( 1)
2 ,
6
в) cosх = 0;
3
г) tg x =
;
3
k
х
2
х
,
6
,
4. 1. Отбор корней в тригонометрическом уравнении с помощью числовой окружности.
Пример 1. cos x + cos 2x – cos 3x = 1.Решение.
cos x – cos 3x – (1 – cos 2x) = 0,
2sin x sin 2x – 2sin2 x = 0,
2sin x (sin 2x – sin x) = 0,
4 sin x sin
x
3x
cos
0;
2
2
sin x 0,
sin x 0,
2
3x
cos
0;
2
5.
x k , k Zx n, n Z
2
3x
m, m Z ;
2
2
y
3
0
2
0
x k , k Z
x 2 n, n Z
2 m
x
, m Z;
3
3
x
5
3
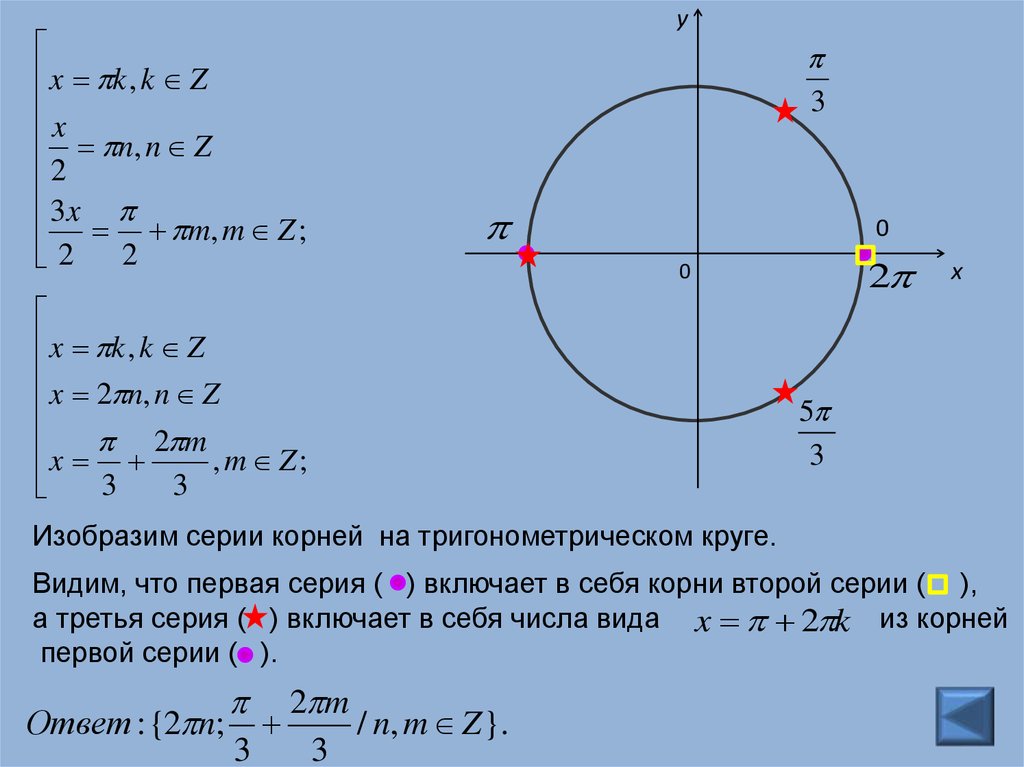
Изобразим серии корней на тригонометрическом круге.
Видим, что первая серия ( ) включает в себя корни второй серии ( ),
а третья серия ( ) включает в себя числа вида x 2 k из корней
первой серии ( ).
Ответ : {2 n;
3
2 m
/ n, m Z }.
3
6.
Пример 2. tg x + tg 2x – tg 3x = 0.Решение.
x
ОДЗ : x
x
2
4
n,
n
,
2
n
, n Z.
6 3
sin x sin 2 x sin 3x
0;
cos x cos 2 x cos 3x
sin x cos 2 x sin 2 x cos x sin 3x
0;
cos x cos 2 x
cos 3x
sin 3x
sin 3x
0;
cos x cos 2 x cos 3x
sin 3 x(cos 3 x cos x cos 2 x)
0;
cos x cos 2 x cos 3x
1
1
sin 3x(cos 3x cos 3x cos x)
2
2
0;
cos x cos 2 x cos 3x
1
1
sin 3x( cos 3x cos x)
2
2
0;
cos x cos 2 x cos 3x
1
sin 3x(cos 3x cos x)
2
0;
cos x cos 2 x cos 3x
1
sin 3x( 2 sin 2 x sin x)
2
0;
cos x cos 2 x cos 3x
sin 3x sin 2 x sin x
0;
cos x cos 2 x cos 3x
7.
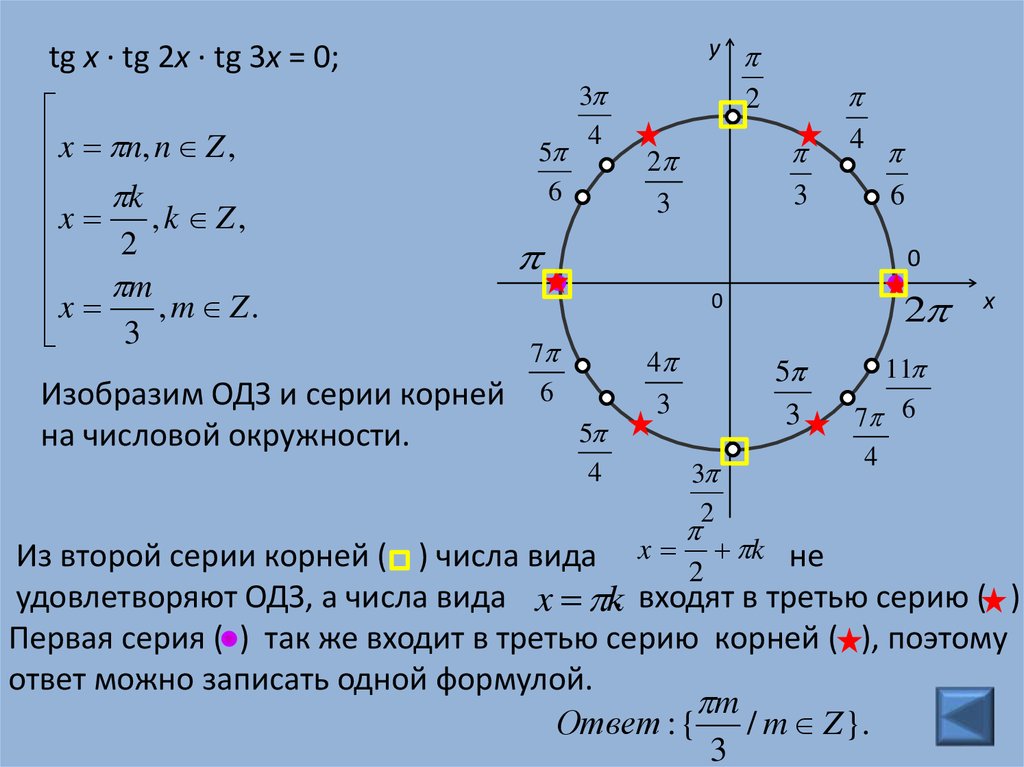
ytg x · tg 2x · tg 3x = 0;
x n, n Z ,
x k , k Z ,
2
m
x
, m Z.
3
Изобразим ОДЗ и серии корней
на числовой окружности.
5
6
3
4
2
3
2
3
4
6
0
2
0
7
6
5
4
4
3
5
3
3
2
x
11
7 6
4
Из второй серии корней ( ) числа вида x 2 k не
удовлетворяют ОДЗ, а числа вида x k. входят в третью серию ( )
Первая серия ( ) так же входит в третью серию корней ( ), поэтому
ответ можно записать одной формулой.
m
Ответ : { / m Z }.
3
8.
2y
cos 3 x
0.
sin 2 x
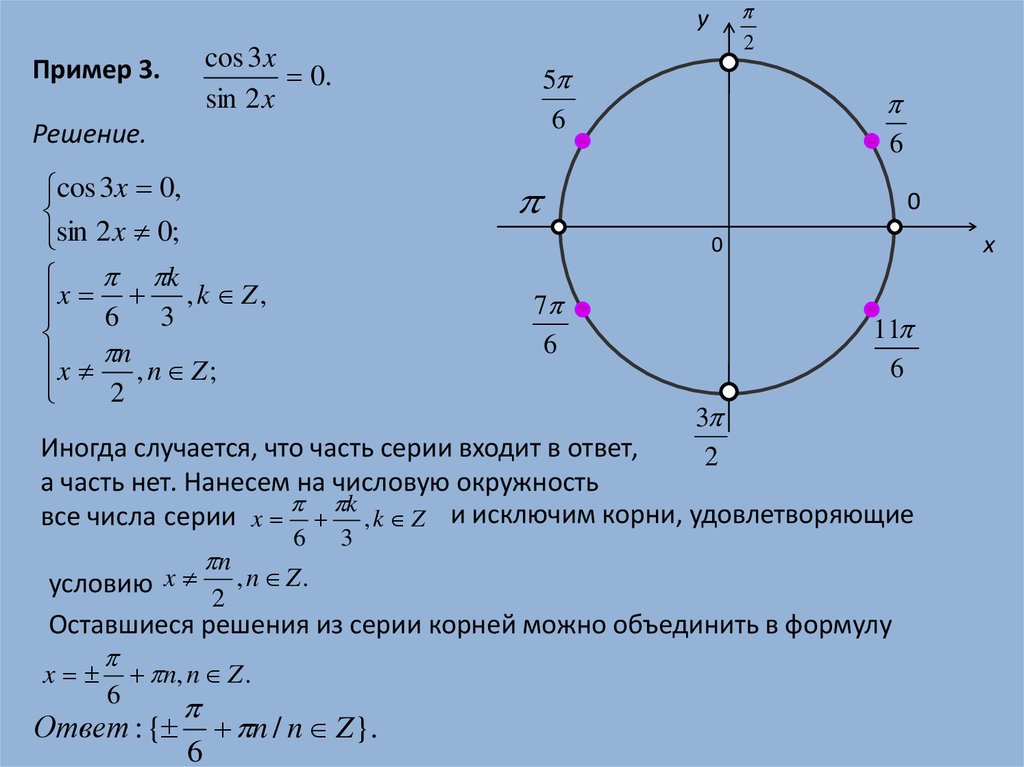
Пример 3.
5
6
Решение.
cos 3x 0,
sin 2 x 0;
6
0
x
0
k
x
,k Z,
6 3
x n , n Z ;
2
7
6
11
6
3
2
Иногда случается, что часть серии входит в ответ,
а часть нет. Нанесем на числовую окружность
все числа серии x k , k Z и исключим корни, удовлетворяющие
условию x
n
2
6
3
, n Z.
Оставшиеся решения из серии корней можно объединить в формулу
x n, n Z .
6
Ответ : {
6
n / n Z }.
9. 2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Пример 1. cos 2 x cos3x
2
4
Решение.
Поскольку наибольшее значение функции y = cos t равно 1, то уравнение
равносильно системе
cos 2 x 1,
3x
cos
1;
4
x k , k Z ,
8 n
x 3 , n Z ;
Решением уравнения является
пересечение серий, то есть нам
надо решить уравнение
k
8 n
;
3
8n
;
3
Получаем
k
k 8t , n 3t , t Z
Итак, x 8 t , t Z .
Ответ : {8 t / t Z }.
10.
Пример 2.x
x
cos sin x 2 sin 2 x cos x sin cos x 2 cos 2 0.
4
4
Решение.
sin( x
4
) cos x 2;
5x
1,
sin
4
cos x 1;
5x
2 n, n Z ,
2
4
x 2 k , k Z ;
2 8 n
x
,n Z,
5
5
x 2 k , k Z ;
5k 1 4n;
5k 1
;
4
k 1
k 1
n k
, где
целое число.
4
4
n
Пусть
k 1
m, тогда
4
k 4m 1, n 5m 1.
x 2 8 m, m Z .
2 8 n
2 k
;
5
5
Итак,
Решением уравнения является
пересечение серий, то есть нам надо
решить уравнение k 1 4n ;
Ответ : {2 8 m / m Z }.
5
11. 3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Пример 1. Найти корни уравнения sin 2x = cos x | cos x |, удовлетворяющиеусловию x [0; 2π].
Решение.
sin 2x = cos x | cos x |;
2sin x· cos x - cos x | cos x |=0;
cos x (2sin x - | cos x |)=0;
cos x 0,
cos x(2 sin x cos x) 0;
cos x 0,
cos x(2 sin x cos x) 0;
12.
cos x 0,x n, n Z ,
2
1
x arctg k , k Z ;
2
cos x 0,
1
x arctg m, m Z .
2
Найдём решение систем
с помощью
числовых окружностей:
cos x ≥ 0
y
cos x < 0
2
y
2
1
2
0
x
0
x
2
1
2
2
1
x 2 n, n Z ,
x arctg 2 m, m Z .
2
1
x arctg 2 k , k Z .
2
3
1
x
,
x
,
x
arctg
Условию x [0;2 ] удовлетворяют числа
2
2
2
1
(для первой системы) и x arctg
(для второй системы).
2
3
1
1
Ответ : { ; ; arctg ; arctg }.
2 2
2
2
13.
Пример 2. Найти все решения уравненияпринадлежащие отрезку [ ;
3
].
2
1 sin 2 x 2 cos 3x 0,
y
Решение.
ОДЗ: cos 3x ≥ 0;
2
2 n 3 x
2
5
6
6
2 n, n Z ;
2 n
2 n
x
, n Z.
6
3
6
3
0
Отметим ОДЗ на тригонометрическом круге:
Отрезку [ ;
2
7
6
x
6
3
2
7 3
3
] принадлежит только один промежуток из ОДЗ, а именно [ ; ].
6 2
2
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos2 3x;
sin 2x = cos 6x;
sin 2x - cos 6x=0;
sin 2 x sin(
2
6 x) 0;
14.
2 cos(4
2 x) sin( 4 x
2 cos( 2 x
4
) sin( 4 x
cos(
2
x
) 0,
4
sin( 4 x ) 0.
4
2
x
n, n Z ,
4
4
4
) 0;
) 0;
2
4 x k , k Z .
4
3 n
x 8 2 ,
x k , k Z .
16 4
Выберем корни,
удовлетворяющие условию задачи.
Из первой серии:
7 3 n 3
6
8
2
2
,n Z;
28 9 12 n 36 , n Z ;
19 12n 27, n Z .
11
Следовательно n=2, то есть x
.
8
Из второй серии:
7 k 3
,n Z;
6 16 4
2
56 3 12 n 72 , n Z ;
53 12n 69, n Z .
Следовательно n=5, то есть x
11 21
Ответ : {
;
}.
8 16
21
.
16
15.
Пример 3. Найти все корни уравнения10 cos 2 (
2
которые удовлетворяют условию x [
Решение.
10sin2 x = – cos 2x + 3;
10sin2 x = 2sin2 x – 1 + 3,
8sin2 x = 2;
1
sin 2 x ;
4
1
sin x ;
2
k
x
(
1
)
k , k Z ,
6
x ( 1) m ( ) m, m Z ;
6
x
6
n, n Z ;
7
2 x) 3,
2
2 19
;
].
3 12
y
2
5
6
6
0
7
6
С помощью числовой окружности получим:
x) sin(
x
3
2
6
16.
Выберем корни, удовлетворяющие условию задачи.Из первой серии: 2 n 19 , n Z ;
3
6
12
8 2 12 n 19 , n Z ;
10 12n 17, n Z .
Следовательно n=0 или n=1, то есть x ,
6
x 7 .
6
2
19
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ;
Из второй серии:
6 12n 21, n Z .
Следовательно n=0 или n=1, то есть
x
,
6
x 5 .
6
Ответ : {
5 7
;
6 6
;
6
}.




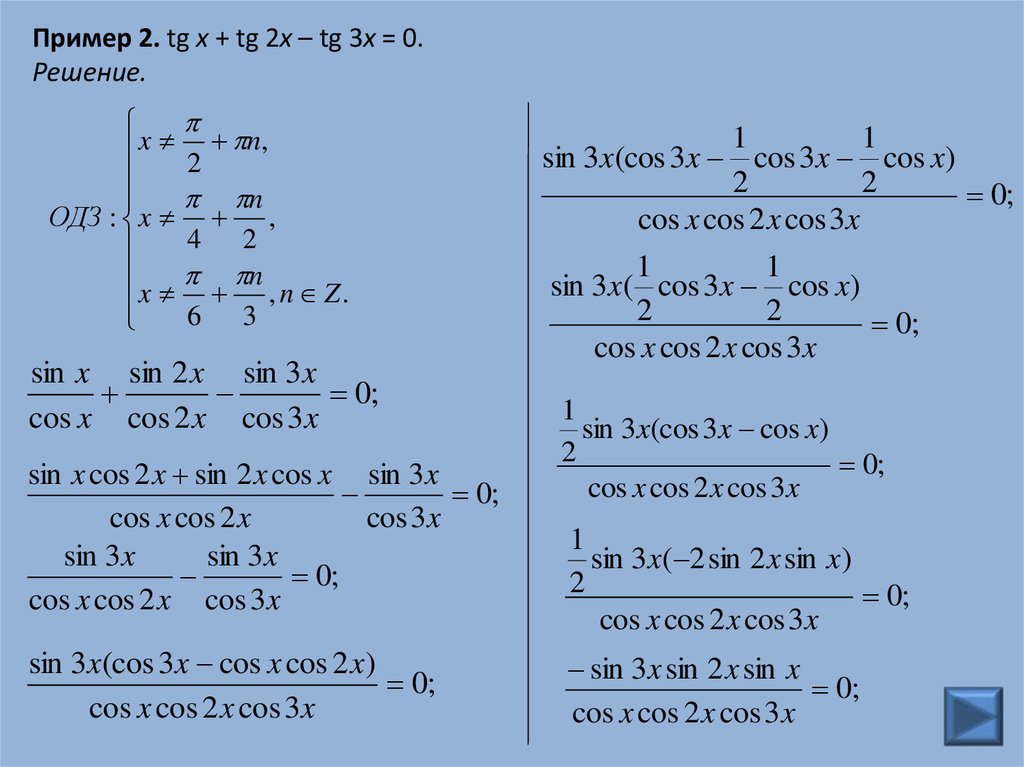








 mathematics
mathematics








