Similar presentations:
Отбор корней при решении тригонометрических уравнений
1. Математический диктант «Простейшие тригонометрические уравнения»
1 вариант2 вариант
В ответе запишите наименьший
положительный корень.
В ответе запишите наибольший
отрицательный корень.
1
cos
(8x 1) 3
6
1
2
В ответе запишите наименьший
положительный корень.
2
( x 5)
tg
3
2
3
(4x 3)
sin
1
( x 9)
2
sin
В ответе запишите наибольший
отрицательный корень.
3
2
8 x
cos
1
6
(4x 1)
1
cos
6
В ответе запишите наибольший
отрицательный корень.
4
6
4
В ответе запишите наименьший
положительный корень.
4
( x 6) 1
В ответе запишите наибольший
отрицательный корень.
3
3
tg
В ответе запишите наименьший
положительный корень.
4
2
2 x 1
sin
3 2
2. Отбор корней при решении тригонометрических уравнений
3. Подстановка корней в имеющиеся ограничения
3Найти корни уравнения cos x
,
2
удовлетворяющие неравенству sin x 0
3
1. Решим уравнение: cos x
2
; x
6
2 k , k Z
2. Проверим для полученных значений х выполнение условия
1
sin x 0 ; sin 2 k sin 0
6
6 2
Первая серия корней является «посторонней»
1
sin 2 k sin 0
2
6
6
Ответ : -
6
2 k , k Z
содержание
4. Перебор значений целочисленного параметра
Найти корни уравнения sin 2 x 0 ,удовлетворяющие неравенству
сosx 0
Наименьший положительный период
для функций у=sin2x, у=cos x
Т 2
Рассмотрим решение уравнения на промежутке
1. Решим уравнение:
sin 2 x 0 ; x
k
2
0 ;2
, k Z
3
х
0
;
;
;
содержатся на помежутке 0;2 .
2. При k=0;1;2;3.;
2
2
3. Отбираем корни уравнения для которых
3
сosx 0 : х 0 ; ;
2
2
4. Исходное уравнение имеет множество решений вида:
х 2 k , k Z и x
k , k Z .
2
Ответ : х 2 k , k Z ; x k , k Z
2
содержание
.
5. Решение неравенства относительно целочисленного параметра
3Решить уравнение cos x
и указать корни
2
принадлежащие отрезку ;0
3
1. Решим уравнение: cos x
; x 2 k , k Z
2
6
2. Подставим корни уравнения в имеющиеся ограничения и
решим уравнение на заданном промежутке:
2 k 0
2 k 0
6
6
1
1
1
2k 0
1 2k 0
6
6
5
1
7
1
2k
2k
6
6
6
6
5
1
k
7
1
k
12
12
12
12
k
0
,
x
Ответ
:
.
k нет целых значений
6
6
содержание
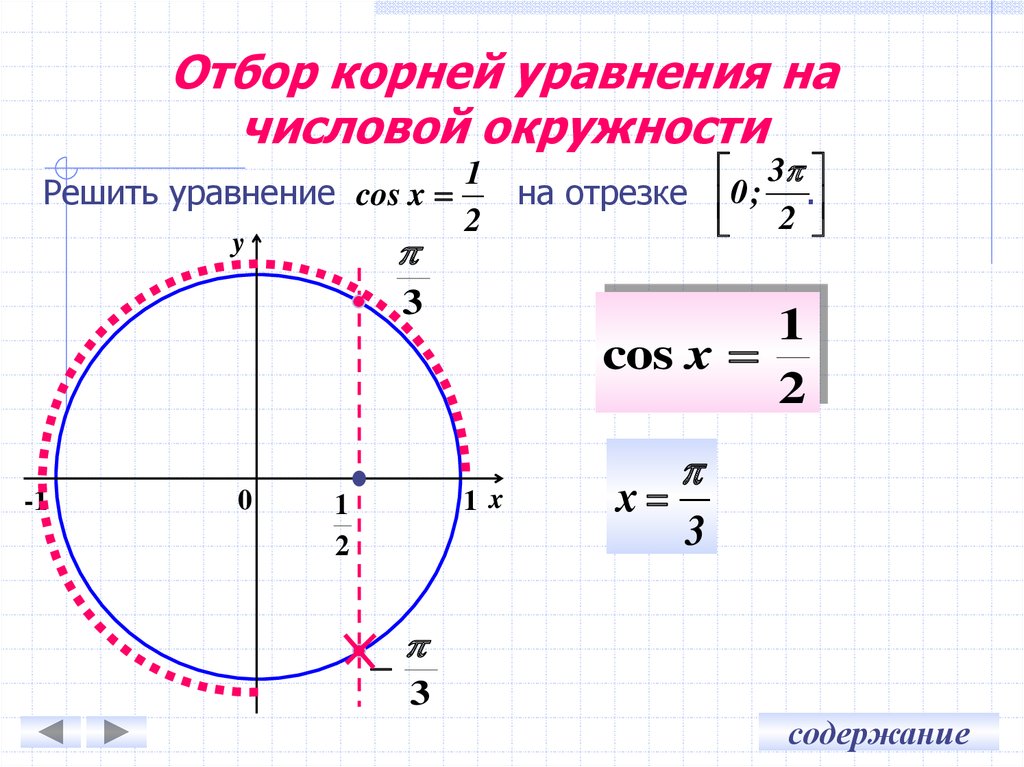
6. Отбор корней уравнения на числовой окружности
1Решить уравнение cos x
2
y
3
-1
0
1
cos x
2
1 x
1
2
3
на отрезке 0 ; .
2
х
3
3
содержание
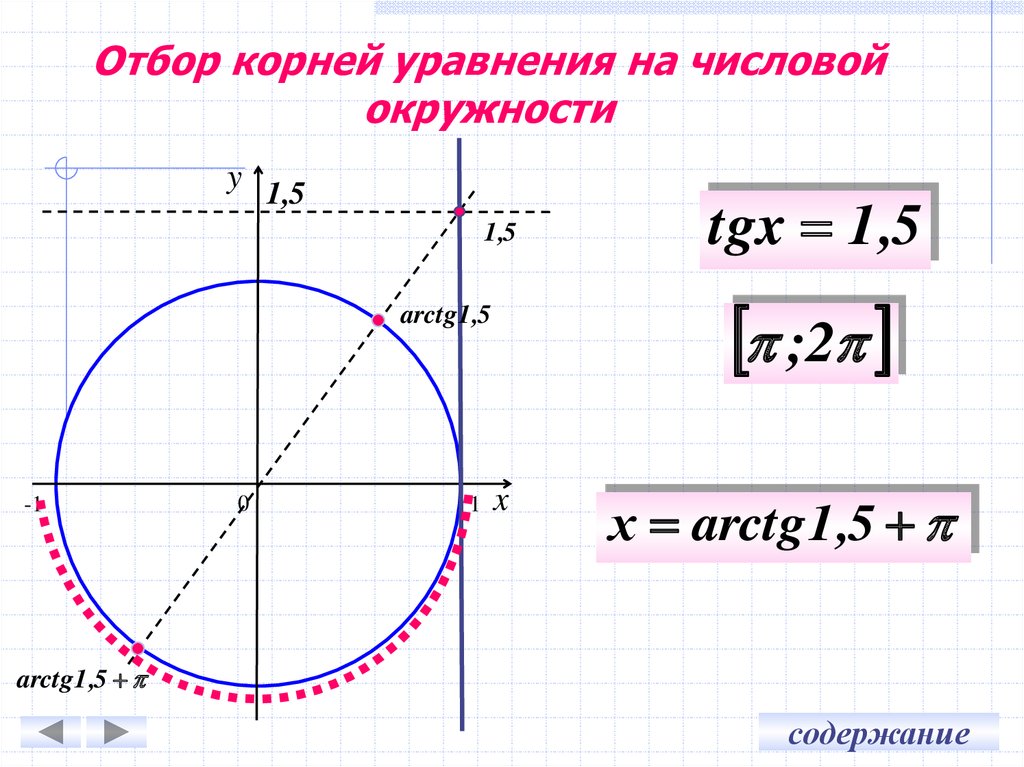
7. Отбор корней уравнения на числовой окружности
y 1,51,5
;2
arctg 1 ,5
-1
0
1
tgx 1 ,5
x
х arctg 1 ,5
arctg1 ,5
содержание
8. Отбор корней уравнения на числовой окружности
1Решить уравнение tgx
3
y
1
3
6
-1
7
6
0
5
на отрезке 0 ; 2 .
1 x
1
tgx
3
х
6
7
х
6
13
х 2
6
6
содержание
9. Отбор корней уравнения на числовой окружности
y5
6
6
1
2
-1
0
1 x
1
sin x
2
3
2 ; 2
5
х
6
содержание







 mathematics
mathematics








