Similar presentations:
Элементарная теория удара
1. Элементарная теория удара
§ 1. Основные понятия теории удара§ 2. Действие ударной силы на материальную
точку
§ 3. Теорема об изменении количества движения
механической системы при ударе
§ 4. Теорема об изменении главного момента
количеств движения при ударе (Теорема
моментов)
§ 5. Прямой центральный удар шара о
неподвижную поверхность
2. § 1. Основные понятия теории удара
Явление, при котором за ничтожномалый промежуток времени скорости
точек тела меняются на конечную
величину, называется ударом
Мгновенной или ударной называют
силу, которая действует в течение
малого промежутка времени, но
достигает таких больших значений, что
её импульс за это время становится
конечной величиной
3.
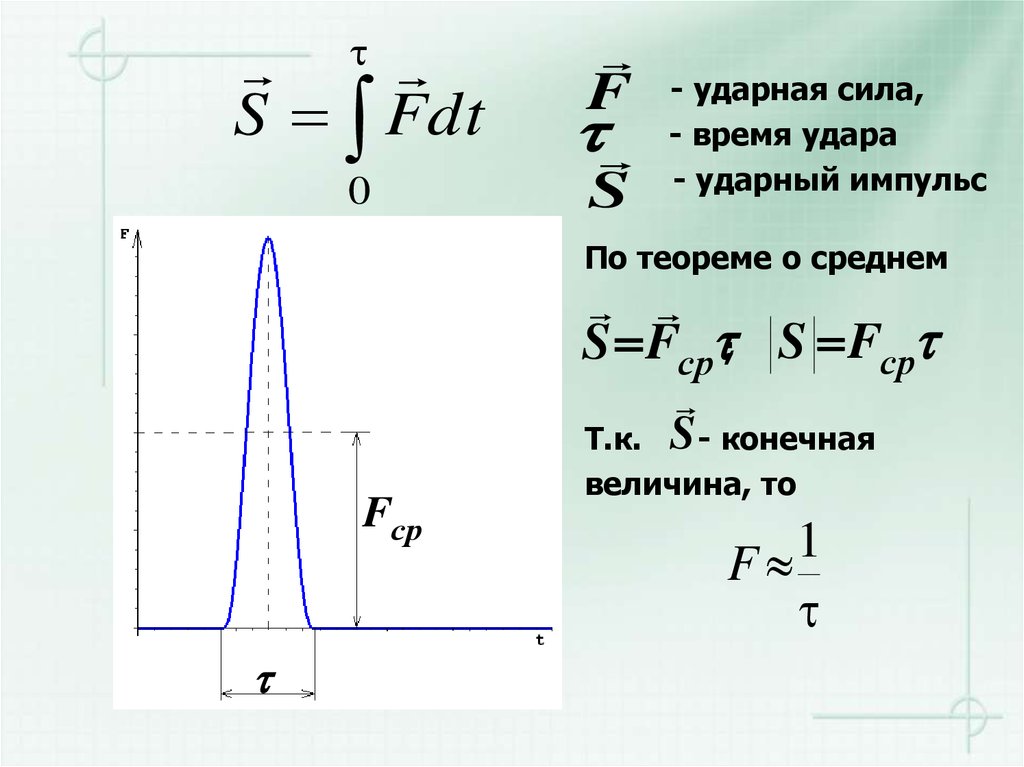
S Fdt0
F
S
- ударная сила,
- время удара
- ударный импульс
По теореме о среднем
S Fср ; S Fср
S - конечная
Fср
Т.к.
величина, то
1
F
4. Пусть соударяются два тела: vA > vB , тела движутся поступательно
AvA
vB
B
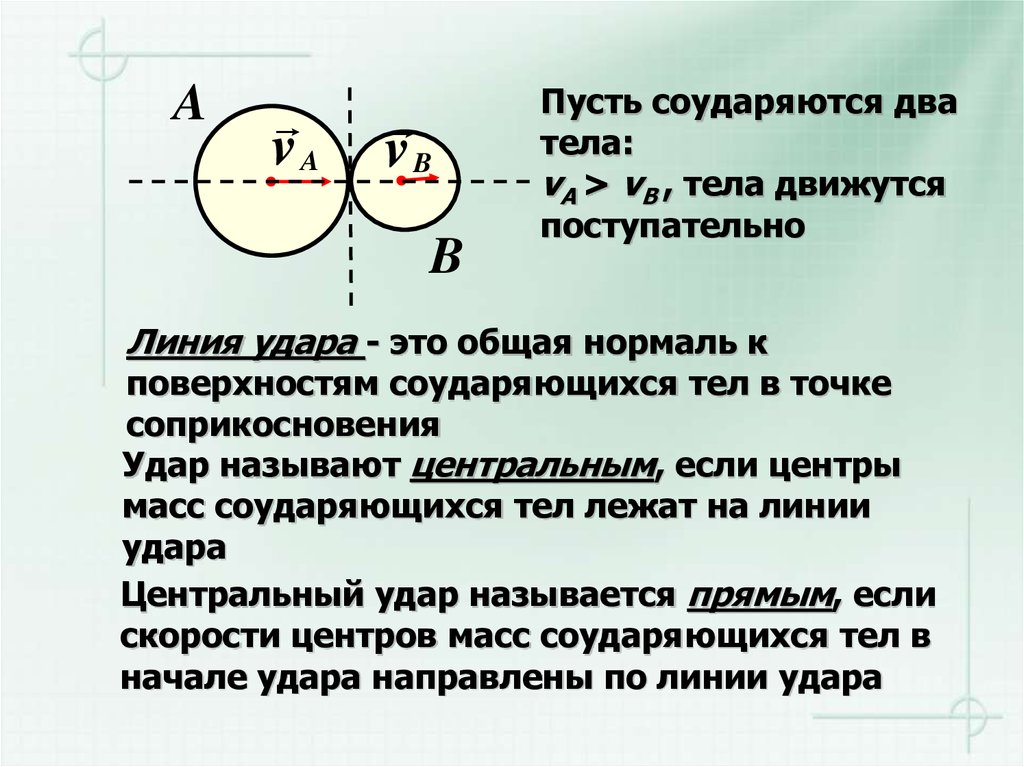
Пусть соударяются два
тела:
vA > vB , тела движутся
поступательно
Линия удара - это общая нормаль к
поверхностям соударяющихся тел в точке
соприкосновения
Удар называют центральным, если центры
масс соударяющихся тел лежат на линии
удара
Центральный удар называется прямым, если
скорости центров масс соударяющихся тел в
начале удара направлены по линии удара
5. Рассмотрим процесс удара. Пусть A, B - абсолютно гладкие тела, удар прямой, центральный. После соприкосновения оба тела
Рассмотрим процесс удара. Пусть A, B абсолютно гладкие тела, удар прямой,центральный. После соприкосновения оба тела
деформируются, vB - увеличивается, vA уменьшается. Процесс деформации
заканчивается, когда vA=vB . Эта часть явления
удара называется фазой деформации.
F
Время этой фазы
F F
F
1
Ударный импульс
S 1 S 1
1
S 1 Fdt
0
- ударный импульс F )
( S1
6. После деформации тела восстанавливают свою форму целиком или частично. Это фаза восстановления.
Время этой фазы . Фаза заканчивается в2
момент отделения тел друг от друга
2
S 2 Fdt
1
1 2 - продолжительность удара.
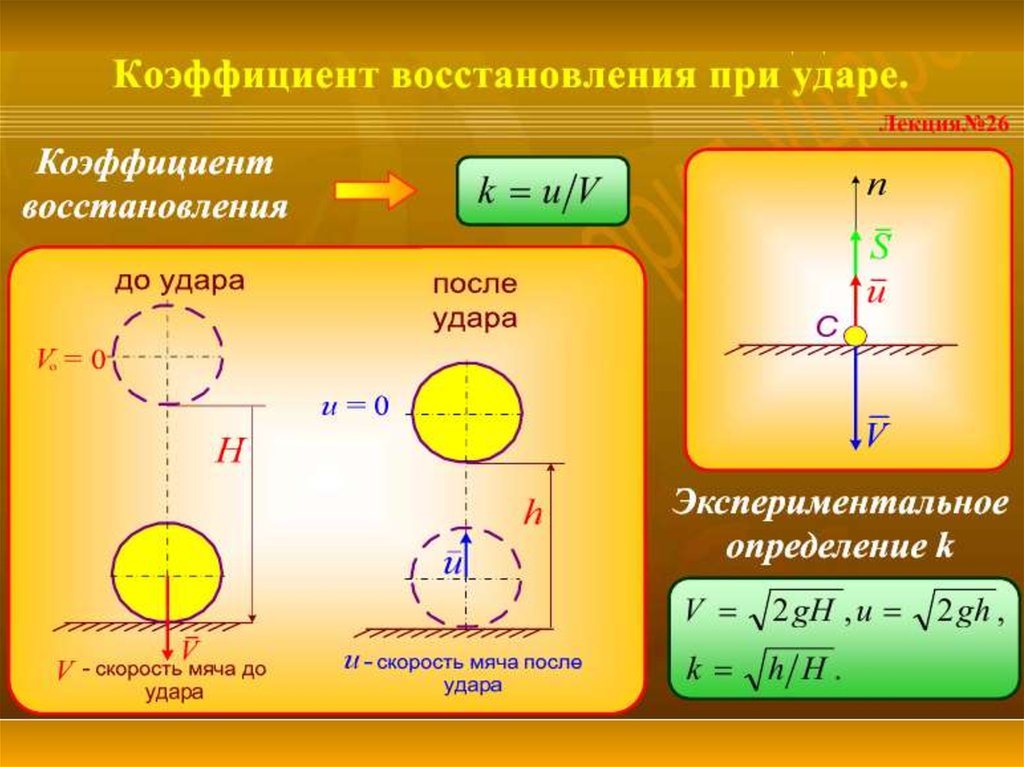
7. Упругость соударяющихся тел оценивается по отношению ударного импульса за фазу восстановления к ударному импульсу за фазу
деформацииS2
k
S1
где k - коэффициент восстановления,
определяется опытным путем:
k 0 S 2 0 - фаза восстановления отсутствует
(абсолютно неупругий удар),
k 1 - абсолютно упругий удар,
0 < k < 1 - упругий удар.
8. § 2. Действие ударной силы на материальную точку
Пусть на точку действует конечная сила Fk и F ударной силы - ,ударная сила. Время действия
v- скорость до удара, u - скорость после удара.
По теореме об изменении количества движения
точки
m u m v Fdt Fk dt
0
0
импульс
S
- ударный
импульс
конечной
силы
ср
S k Fk
по теореме о среднем
малой величиной
можно пренебречь
9. Теорема Изменение количества движения точки за время удара равно ударному импульсу, приложенному к точке.
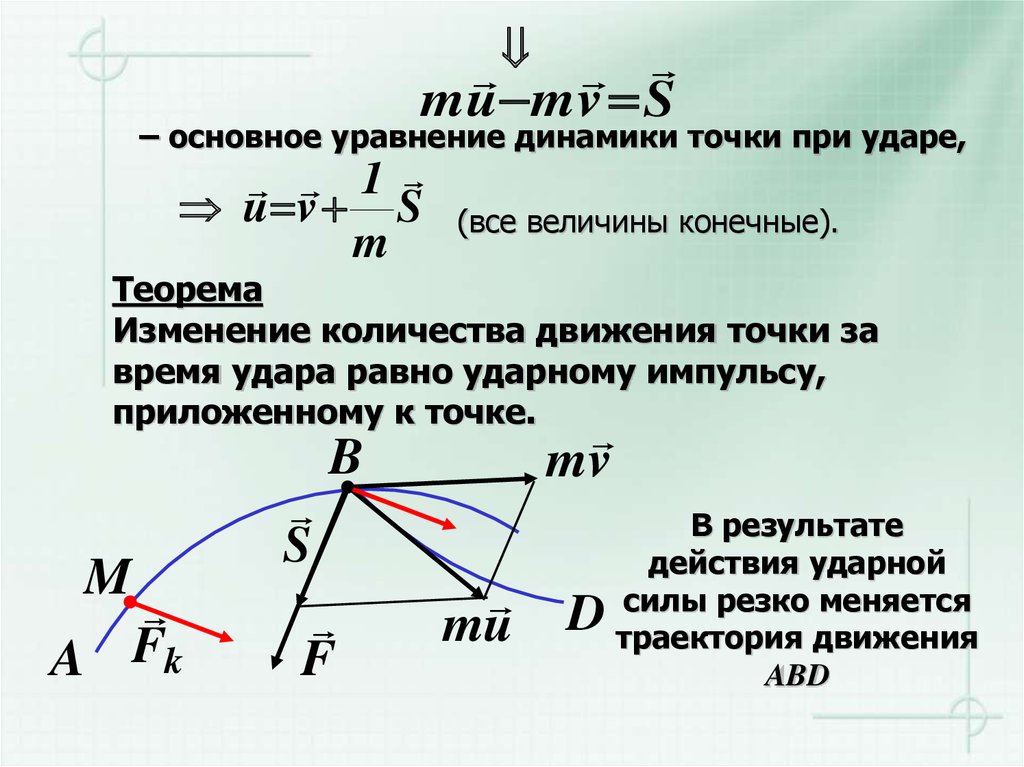
m u m v S– основное уравнение динамики точки при ударе,
1
u v S
m
(все величины конечные).
Теорема
Изменение количества движения точки за
время удара равно ударному импульсу,
приложенному к точке.
M
A Fk
S
mv
B
F
mu
D
В результате
действия ударной
силы резко меняется
траектория движения
ABD
10. Выводы
s vdt - расстояние, пройденное за время удара,0
s v ср s 0
Выводы
1. Действием конечных сил за время удара
можно пренебречь
2. Перемещением точки за время действия
ударных сил можно пренебречь
3. Действие ударных сил на точку выражается
в быстром изменении величины и
направления скорости
11. § 3. Теорема об изменении количества движения механической системы при ударе
Для механической системы, состоящей из nматериальных точек, на которую действуют
как конечные, так и ударные силы,
справедливо
Q Q0 S k
e
k
Теорема
Изменение количества движения
механической системы за время удара равно
сумме всех внешних ударных импульсов,
действующих на систему.
12. В проекциях:
Еслиe
Q x Q0 x S k x
k
e
Q y Q0 y S k y
k
e
Q z Q0 z S k z
e
S k 0
, то
k
Q Q0.
k
Вывод: внутренние ударные импульсы не могут
изменить количество движения системы.
Если Q Muc и Q0 Mv c , то
e
Muc Mv c S k - определяет изменение
k
скорости центра масс при
ударе.
13. § 4. Теорема об изменении главного момента количеств движения при ударе (теорема моментов)
Рассмотрим систему из n материальных точекe - равнодействующая внешних ударных
импульсов,
k
S
i
- равнодействующая внутренних ударных
S k импульсов,
действующих на каждую точку,
i
e
m k uk m k v k S k S k
14. Векторы приложены к точке, которая за время удара не перемещается, тогда, по теореме Вариньона,
e im 0 ( m k uk ) m 0 ( m k v k ) m 0 ( S k ) m 0 ( S k )
Теперь просуммируем
m 0 ( m k uk ) m0 ( m k v k )
e
i
m 0 ( S k ) m 0 ( S k )
e
K 0 2 K 0 1 m0 ( S k )
15. Теорема Изменение за время удара кинетического момента системы относительно какого-либо центра равно сумме моментов
относительнотого же центра всех действующих на систему
внешних ударных импульсов.
В проекциях:
e
K 0 2 x K 0 1 x m 0 x ( S k )
e
K 0 2 y K 0 1 y m0 y ( S k )
e
K 0 2 z K 0 1 z m0 z ( S k )
Вывод: внутренние ударные импульсы не
меняют кинетический момент системы.
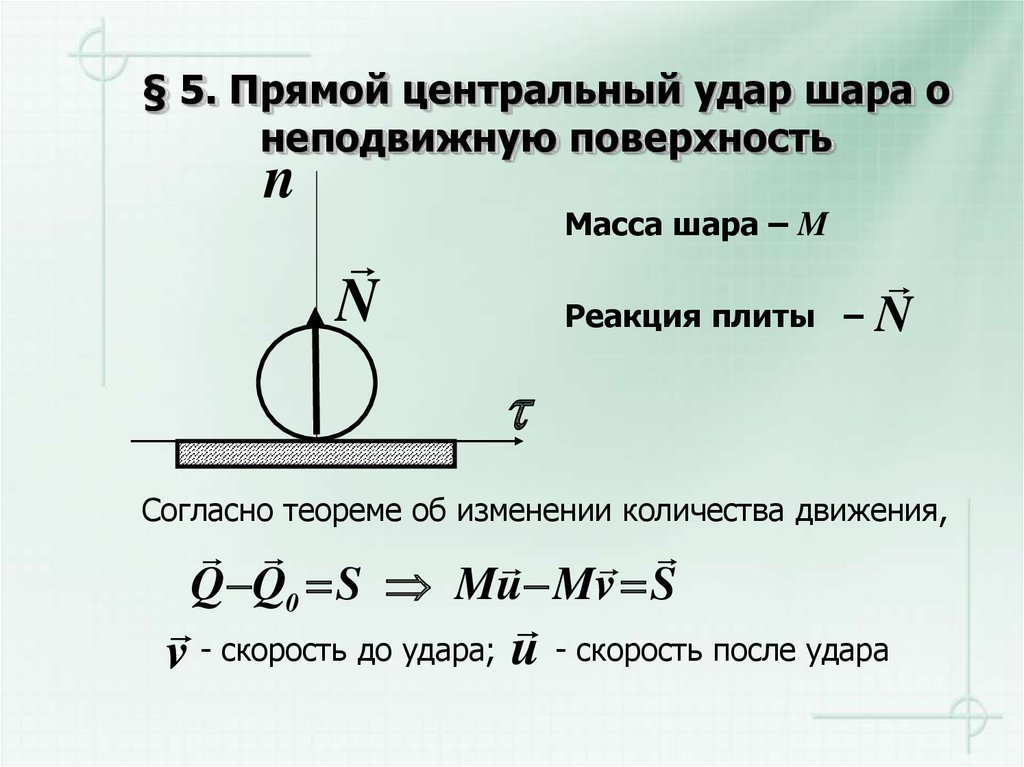
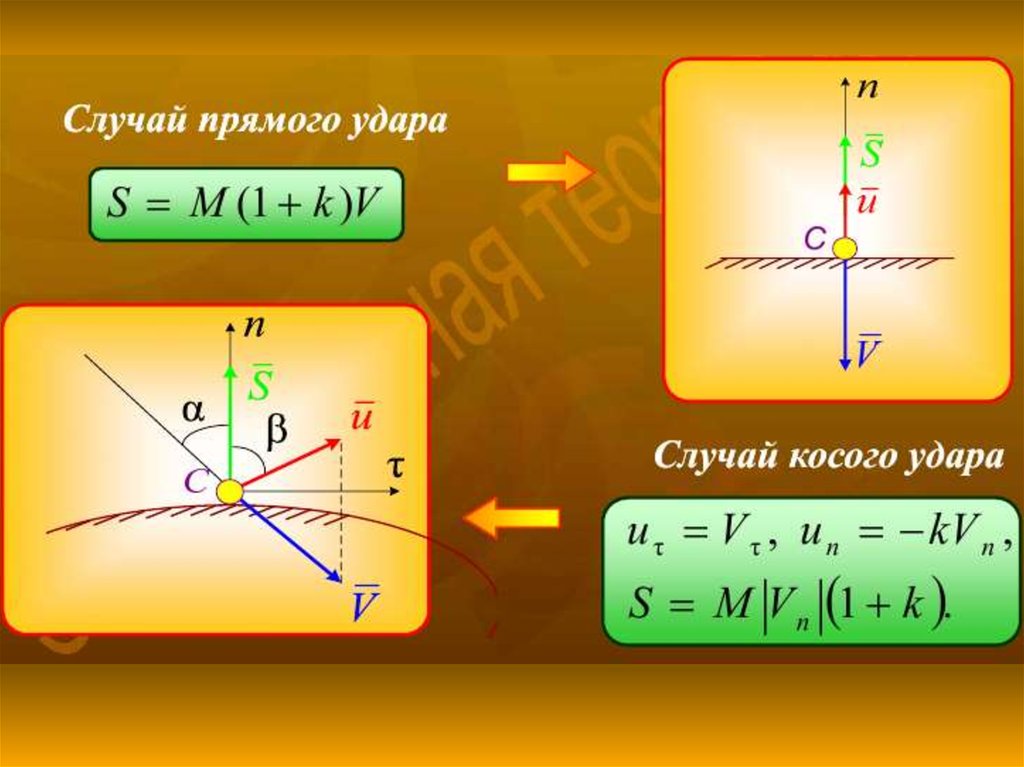
16. § 5. Прямой центральный удар шара о неподвижную поверхность
nМасса шара – M
N
Реакция плиты
–N
Согласно теореме об изменении количества движения,
Q Q0 S Mu Mv S
- скорость до удара; u - скорость после удара
v
17. Проектируем на нормаль:
Т.к. удар прямой иMu Mv S
un u v n v S n S, то
(5 )
0 Mv S 1 ; Mu 0 S 2
S2 u
k
S1 v
Поскольку
Mun Mv n S n
S 1 - ударный импульс за
фазу деформации
S 2 - ударный импульс за
фазу восстановления
S M ( v kv ); S Mv ( k 1 )
v 2 gh
и
u 2 gh1
,то
h1
k
h















 physics
physics








