Тригонометрия. Таблица значений тригонометрических функций

1. Тригонометрия

в двух словах

2. Числовая окружность

Мы хорошо представляем, что такое числовая прямая – это прямая, на которой мы
отмечаем числа.
Что получится, если мы согнём числовую прямую в кольцо?

3.

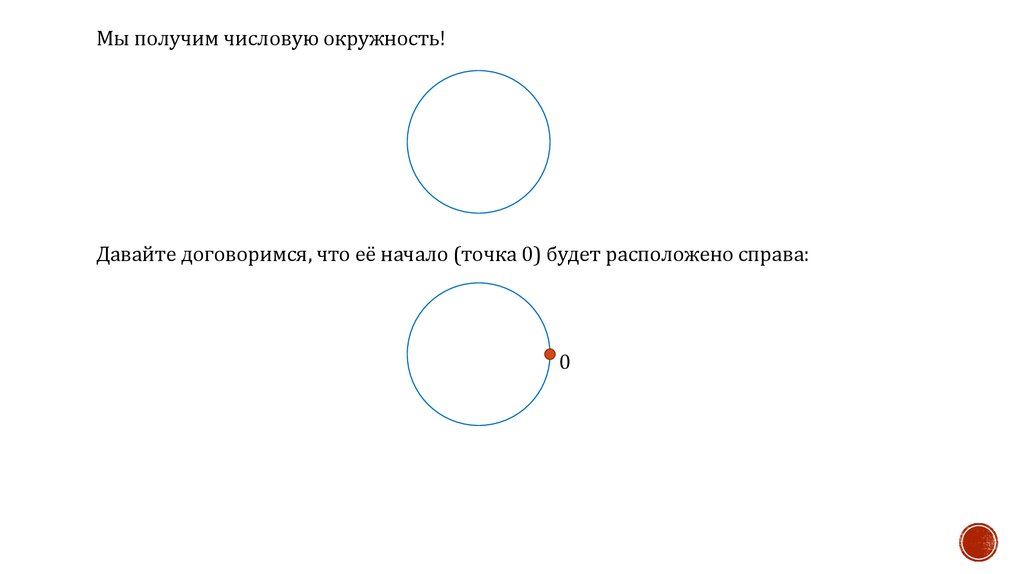
Мы получим числовую окружность!
Давайте договоримся, что её начало (точка 0) будет расположено справа:
0

4. Движение по числовой окружности

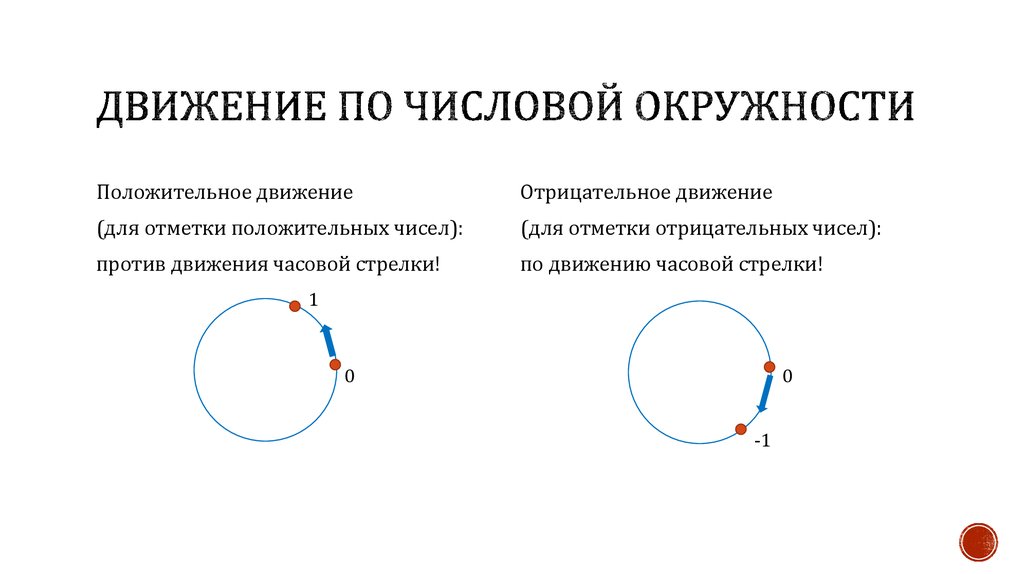
Положительное движение
Отрицательное движение
(для отметки положительных чисел):
(для отметки отрицательных чисел):
против движения часовой стрелки!
по движению часовой стрелки!
1
0
0
0
-1

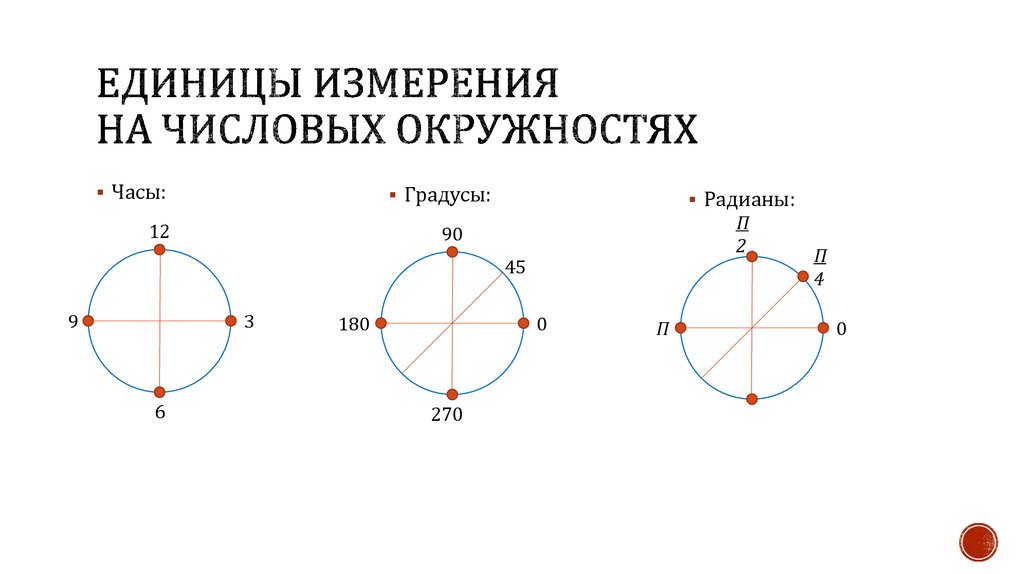
5. Единицы измерения на числовых окружностях

Часы:
Градусы:
12
Радианы:
П
2
90
45
9
3
6
180
0
270
П
П
4
0

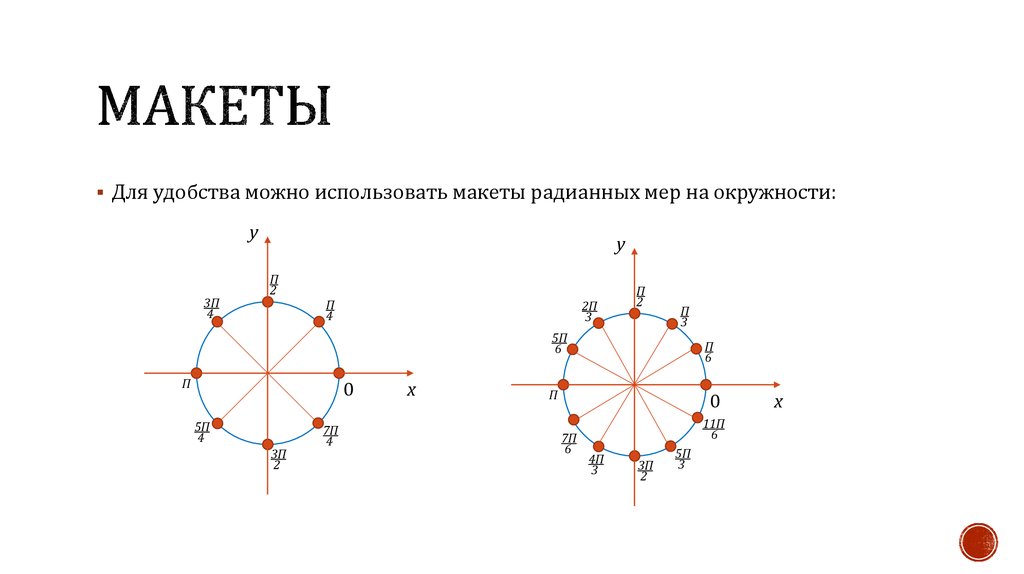
6. Макеты

Для удобства можно использовать макеты радианных мер на окружности:
у
3П
4
у
П
2
П
4
2П
3
П
2
П
3
5П
6
П
0
5П
4
3П
2
7П
4
х
П
6
П
0
7П
6
11П
6
4П
3
3П
2
5П
3
х

7. Что такое синус (sin)?

Поместим числовую окружность на координатную плоскость:
у
Обозначим проекцию точки П/4 на оси 0у.
П
2
М
П
Полученная точка M и есть синус (sin П/4)
П
4
0
х

8. Что такое косинус (cos)?

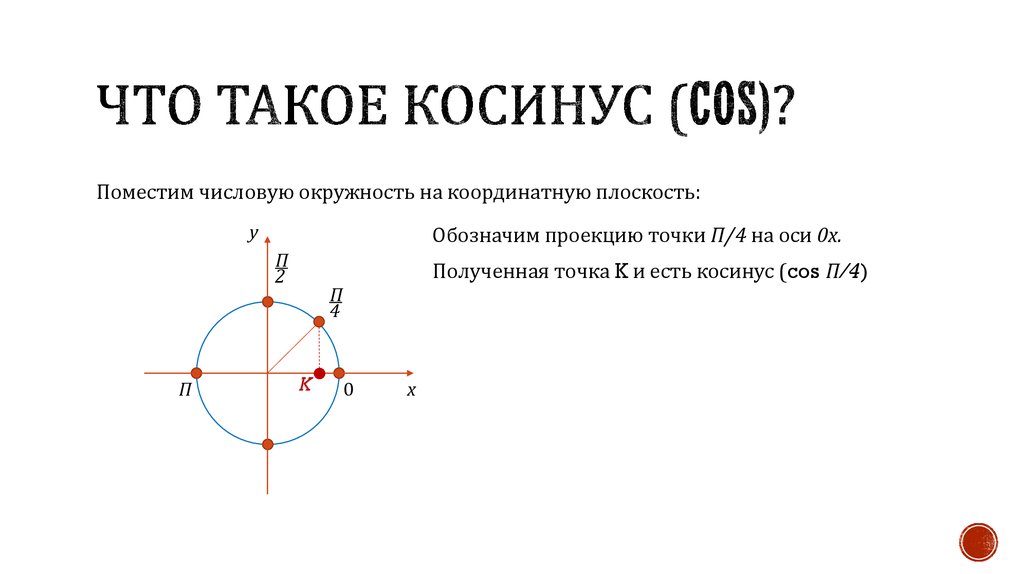
Поместим числовую окружность на координатную плоскость:
у
Обозначим проекцию точки П/4 на оси 0х.
П
2
П
Полученная точка K и есть косинус (cos П/4)
П
4
K
0
х

9. Как найти значение синуса?

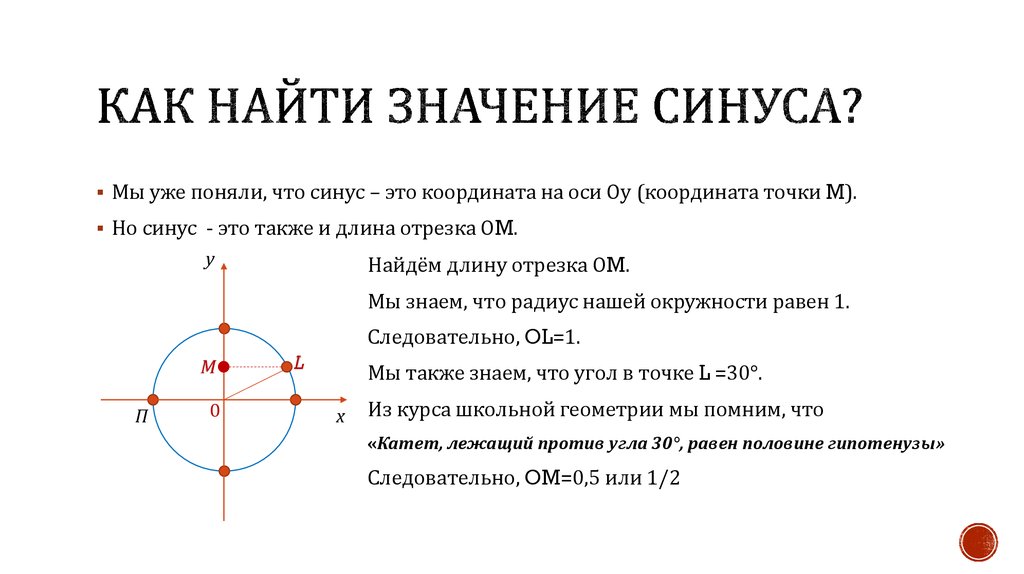
Мы уже поняли, что синус – это координата на оси Оу (координата точки M).
Но синус - это также и длина отрезка ОM.
у
Найдём длину отрезка ОM.
Мы знаем, что радиус нашей окружности равен 1.
Следовательно, OL=1.
М
П
0
L
Мы также знаем, что угол в точке L =30°.
х
Из курса школьной геометрии мы помним, что
«Катет, лежащий против угла 30°, равен половине гипотенузы»
Следовательно, OM=0,5 или 1/2

10. Выполните подобное вычисление 1000 раз и…

…и, с большой долей вероятности, вы станете
сумасшедшим гением в тригонометрии.

11. Принцип «хорошей лени»

К счастью, большинство из нас очень скоро заметит, что производит одни и те же
вычисления много раз. А не проще ли записать уже найденные однажды значения,
например, в таблицу?

12. Таблица значений тригонометрических функций

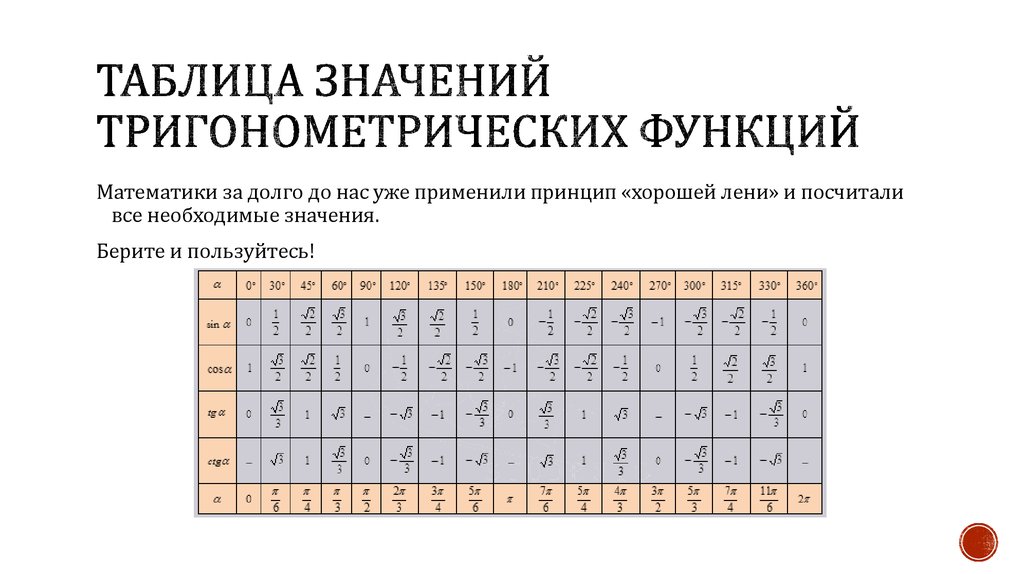
Математики за долго до нас уже применили принцип «хорошей лени» и посчитали
все необходимые значения.
Берите и пользуйтесь!