Симетрія відносно прямої (осьова симетрія)

1.

Симетрія відносно прямої
(осьова симетрія)
0011 0010 1010 1101 0001 0100 1011
l
XO=OX1
X
O
X1
XX1┴ l
1
2
4
Точки X і X1 називаються симетричними
відносно
прямої
l, якщо ця пряма
перпендикулярна до відрізка XX1
і
проходить через його середину

2.

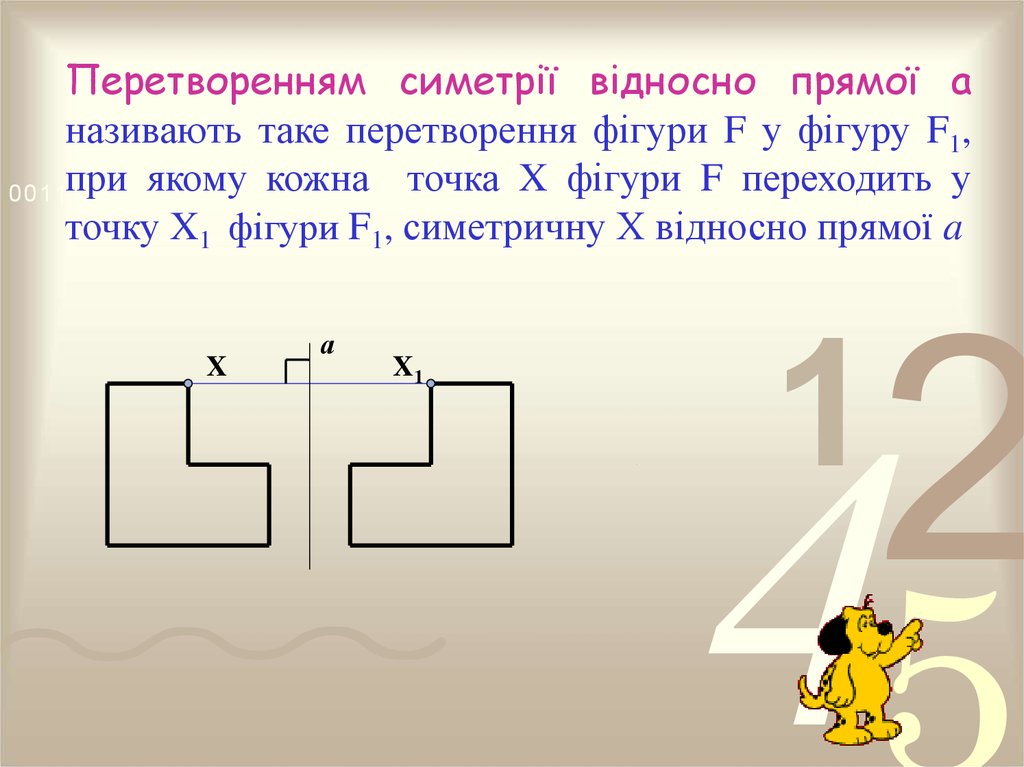
Перетворенням симетрії відносно прямої a
називають таке перетворення фігури F у фігуру F1,
якому
X фігури F переходить у
0011при
0010 1010
1101кожна
0001 0100точка
1011
точку X1 фігури F1, симетричну Х відносно прямої a
X
а
X1
1
2
4

3.

Побудова
0011 0010 1010 1101 0001 0100 1011
1
2
4

4.

Якщо перетворення симетрії відносно прямої l
переводить фігуру F у себе, то така фігура
0011 0010 називається
1010 1101 0001 0100
1011
симетричною
відносно прямої l ,
а сама пряма l - віссю симетрії фігури F
1
2
4

5. Симетрія відносно прямої

0011 0010 1010 1101 0001 0100 1011
В природі і житті
1
2
4

6.

0011 0010 1010 1101 0001 0100 1011
1
2
4

7.

0011 0010 1010 1101 0001 0100 1011
1
2
4

8.

0011 0010 1010 1101 0001 0100 1011
1
2
4