Симетрія відносно точки та симетрія відносно площини

1. Симетрія відносно точки та симетрія відносно площини

2. Завдання уроку:

Поглибити знання про симетрію у просторі та її
властивості
Визначити, чи зустрічається симетрія у
навколишньому світі
Навчитися використовувати властивості симетрії до
розв’язування геометричних задач
Навчитися будувати симетричні фігури

3. Актуалізація опорних знань

“ПРАВДА чи БРЕХНЯ?”

4. Голосуйте картками: зелена – правда, червона - брехня

1) Вісь Oz називається віссю аплікат.
2) Правильний трикутник при переміщенні
може перейти у прямокутний.
3) Якщо точка А(8; 6 ; 3)
В(5; 4 ; 0), а
точка М(-1; 0; -1)
К(- 4; - 2; 2), тоді це
перетворення – паралельне перенесення
4) Якщо паралельне перенесення задано
формулами x' = x – 2, y' = y + 1, z' = z + 2,
тоді М (2; 3; – 4)
К (0; 4; – 2)

5. Вивчення нового матеріалу

6.

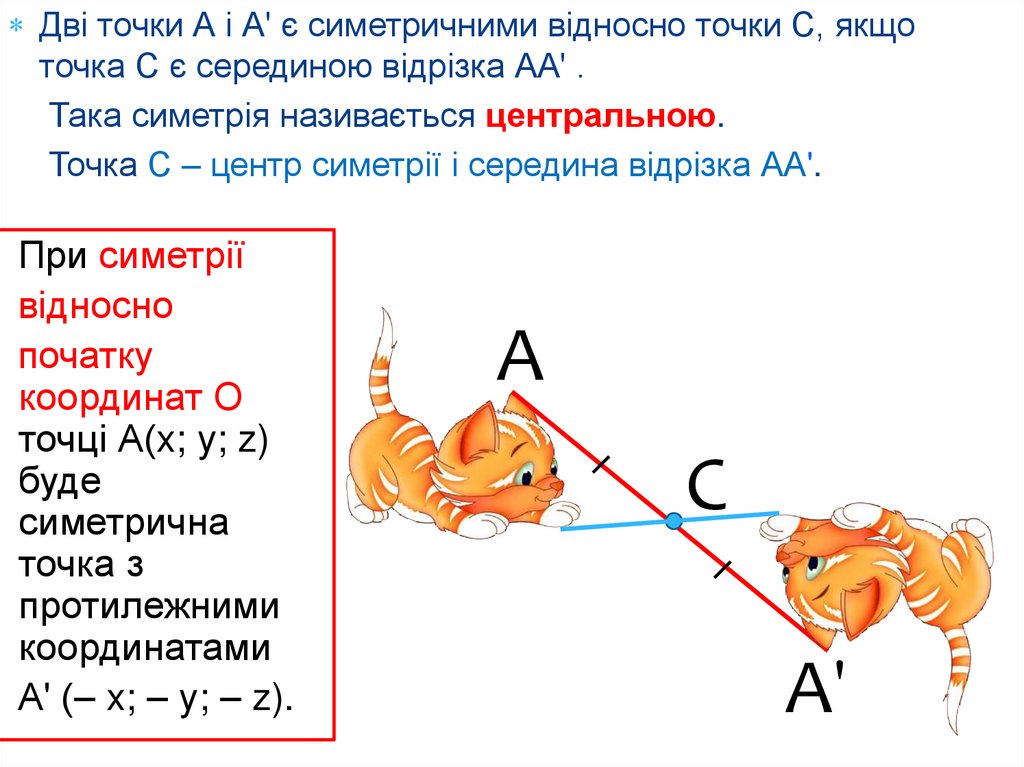
Дві точки А і А' є симетричними відносно точки С, якщо
точка С є серединою відрізка АА' .
Така симетрія називається центральною.
Точка С – центр симетрії і середина відрізка АА'.
При симетрії
відносно
початку
координат О
точці А(x; y; z)
буде
симетрична
точка з
протилежними
координатами
А' (– x; – y; – z).
А
С
А'

7.

Дві точки А і А' є симетричними відносно прямої m, якщо
пряма m є серединним перпендикуляром до відрізка АА' .
Така симетрія називається осьовою.
Пряма m – вісь симетрії.
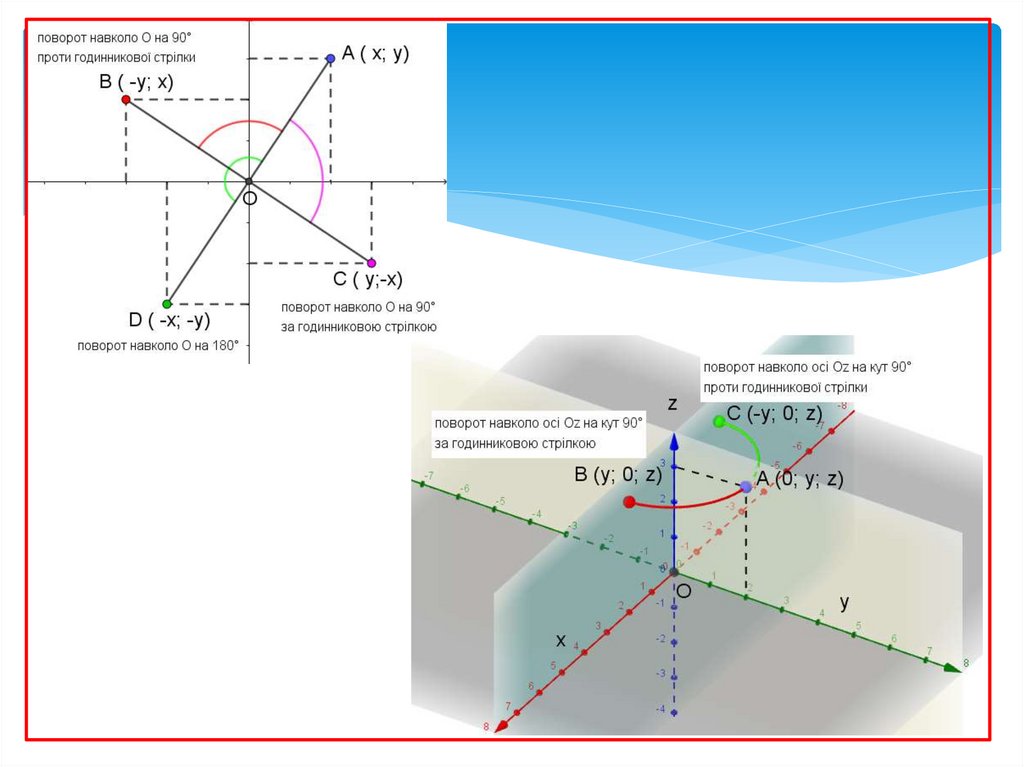
При симетрії відносно координатної осі точці
А(x; y; z) буде симетрична така точка А', у якої
відповідна даній осі координата буде без зміни, а
інші координати
будуть
протилежними
числами.
А
m
А'

8.

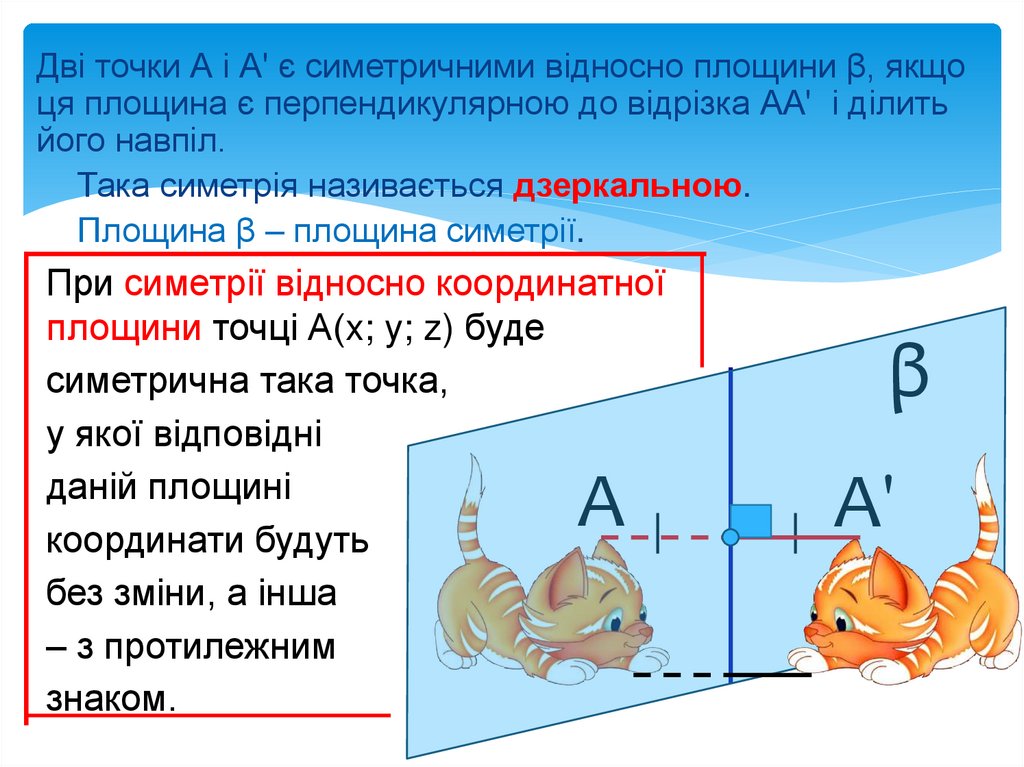
Дві точки А і А' є симетричними відносно площини β, якщо
ця площина є перпендикулярною до відрізка АА' і ділить
його навпіл.
Така симетрія називається дзеркальною.
Площина β – площина симетрії.
При симетрії відносно координатної
площини точці А(x; y; z) буде
симетрична така точка,
у якої відповідні
даній площині
координати будуть
без зміни, а інша
– з протилежним
знаком.
А
β
А'

9.

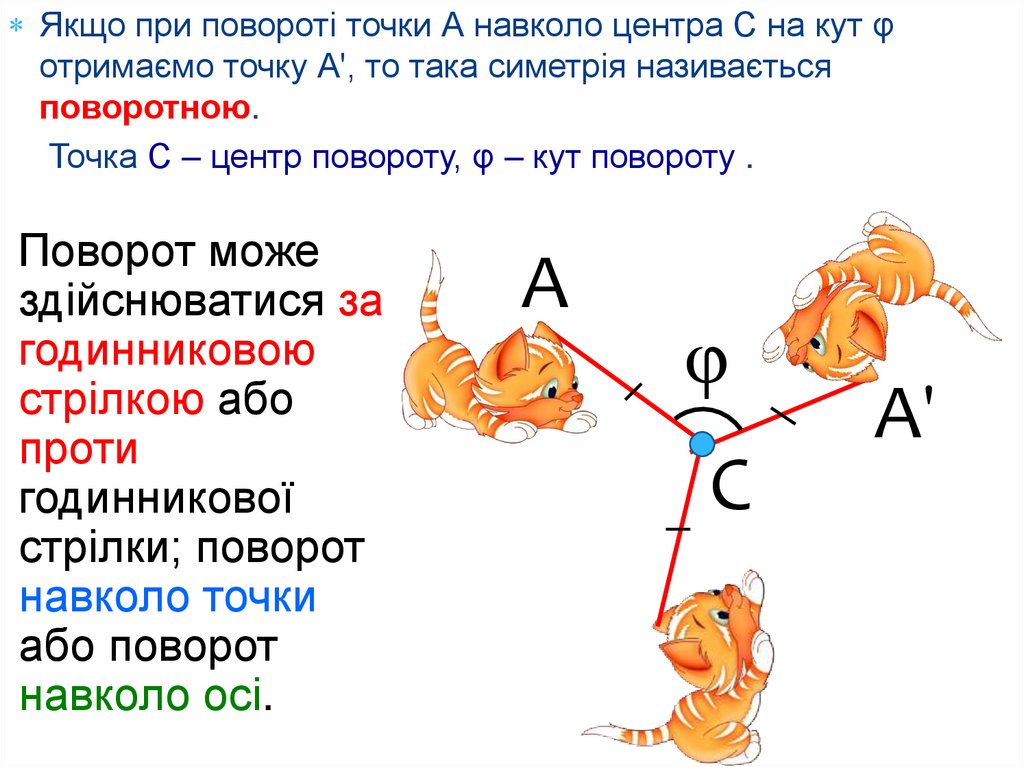
Якщо при повороті точки А навколо центра С на кут φ
отримаємо точку А', то така симетрія називається
поворотною.
Точка С – центр повороту, φ – кут повороту .
Поворот може
здійснюватися за
годинниковою
стрілкою або
проти
годинникової
стрілки; поворот
навколо точки
або поворот
навколо осі.
А
φ
С
А'

10.

11.

Якщо точка А здійснює перенесення вздовж осі, доповнене
обертанням навколо неї на кут 90°, то така симетрія
називається гвинтовою.
Поворот на кут 180° є
центральною симетрією.
Поворот на кут 90° є
осьовою симетрією.
Якщо при повороті фігура
переходить сама у себе,
то це – переносна
симетрія.
Переносна та гвинтова
симетрії є нетрадиційними
видами симетрії .

12. Знання збираються по краплині, як вода в долині

Українське прислів’я

13.

Закріплення нового
матеріалу

14.

Групова робота із
завданнями

15.

№1
Запишіть координати точок, симетричних
точці А (3;– 4; 1) відносно:
1) Початку координат
(– 3; 4; – 1)
2) Площини xy ( 3;– 4; – 1)
3) Площини xz ( 3; 4; 1)
4) Осі Oz
(– 3; 4; 1)

16.

№2
Точки А (5;– 3; 4) та В (– 3; 1; – 2) симетричні
відносно точки С. Які її координати?
Розв’язання:
За означенням центральної симетрії точка
С – середина відрізка АВ. Тоді:
5 ( 3 )
xc =
= 1;
2
4 ( 2 )
zc =
=
1;
2
Відповідь: С ( 1;– 1; 1)
3 1
уc =
= –1;
2

17.

№3
Точки E (– 3; 8; 7) та F симетричні відносно
площини ху. Знайдіть довжину відрізка EF.
Розв’язання:
За властивістю дзеркальної симетрії
будуть такі координати точки F :
(– 3; 8; –7).
Тоді за формулою довжини відрізка
маємо:
2
2
2
EF = ( 3 ( 3 )) ( 8 8 ) ( 7 7 ) =
= 196 14
Відповідь: EF = 14.