Similar presentations:
Симетрія у просторі та її властивості (10 клас)
1. Симетрія у просторі та її властивості
Урок геометріїу 10 класі
Кругляківської ЗОШ
І-ІІІ ступенів
Кальченко Вікторія Іванівна
2.
Перевірка домашньогозавдання
3.
№1Паралельне перенесення задано формулою:
х' = х – 4; y ' = y + 2; z ' = z – 6.
1) У яку точку перейде М(4; – 2; 7)?
Розв’язання : М ' (4 – 4; – 2 + 2; 7 – 6),
( 0; 0; 1).
2) Яка точка переходить у точку N ' (– 2; 0; – 1)?
Розв’язання: – 2 = x – 4; x = 2,
0 = y + 2; y = – 2,
– 1 = z – 6; z = 5.
N ( 2; – 2 ; 5).
4.
№2При паралельному перенесенні точка
М ( 2; – 3; 7) переходить у точку К (– 3; –5; 0).
Складіть формули паралельного перенесення.
Розв’язання : – 3 = 2 + а; а = – 5 ,
– 5 = – 3 + b; b = – 2,
0 = 7 + c; c = – 7 .
х' = х – 5; y ' = y – 2; z ' = z – 7.
5.
№3Точка А (– 3; 1; – 6)
А' (2; 3; – 9),
точка В (4; – 6; 3)
В' (9; – 4; 6).
Чи існує таке паралельне перенесення?
Розв’язання :
для точок А і А' маємо:
a = 5;
b = 2;
c = – 3.
для точок B і B' маємо:
a = 5;
b = 2;
c = 3.
Відповідні коефіцієнти с різні, отже це не є
паралельним перенесенням.
6. Завдання уроку:
7. Завдання уроку:
Поглибити знання про симетрію упросторі та її властивості
Визначити, чи зустрічається симетрія у
навколишньому світі
Навчитися використовувати
властивості симетрії до розв’язування
геометричних задач
Навчитися будувати симетричні фігури
8. Актуалізація опорних знань
“ПРАВДА чи БРЕХНЯ?”9. Голосуйте картками: зелена – правда, червона - брехня
1) Вісь Oz називається віссю аплікат.2) Правильний трикутник при переміщенні
може перейти у прямокутний.
3) Якщо точка А(8; 6 ; 3)
В(5; 4 ; 0), а
точка М(-1; 0; -1)
К(- 4; - 2; 2), тоді це
перетворення – паралельне перенесення
4) Якщо паралельне перенесення задано
формулами x' = x – 2, y' = y + 1, z' = z + 2,
тоді М (2; 3; – 4)
К (0; 4; – 2)
10. Вивчення нового матеріалу
11.
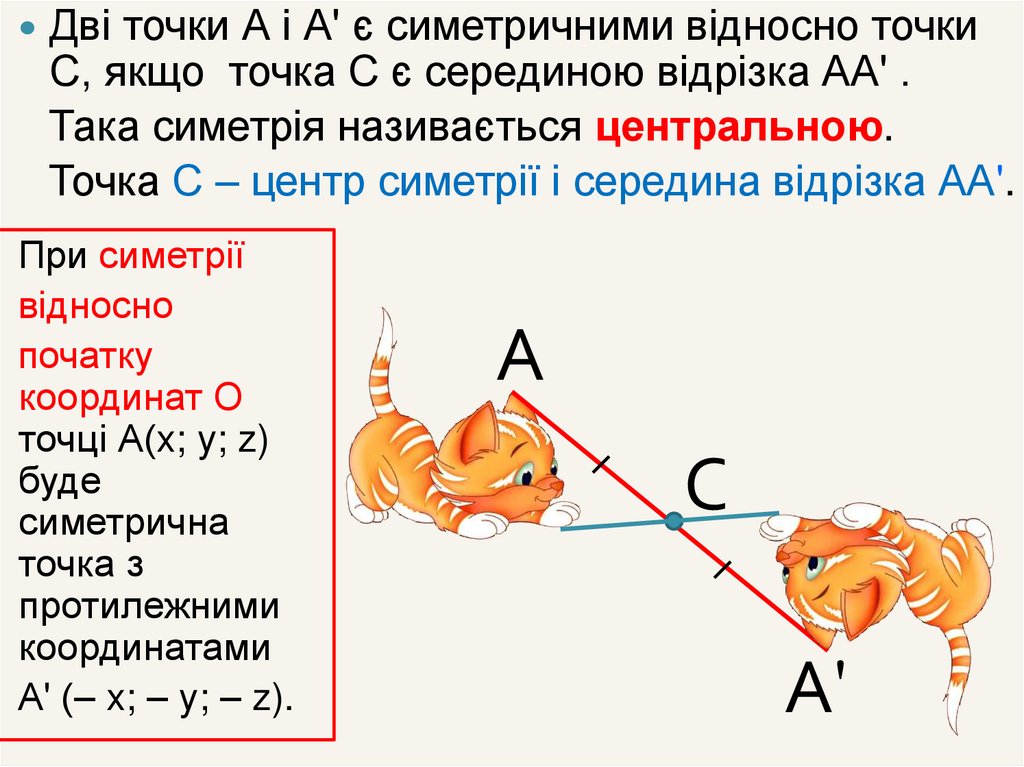
Дві точки А і А' є симетричними відносно точкиС, якщо точка С є серединою відрізка АА' .
Така симетрія називається центральною.
Точка С – центр симетрії і середина відрізка АА'.
При симетрії
відносно
початку
координат О
точці А(x; y; z)
буде
симетрична
точка з
протилежними
координатами
А' (– x; – y; – z).
А
С
А'
12.
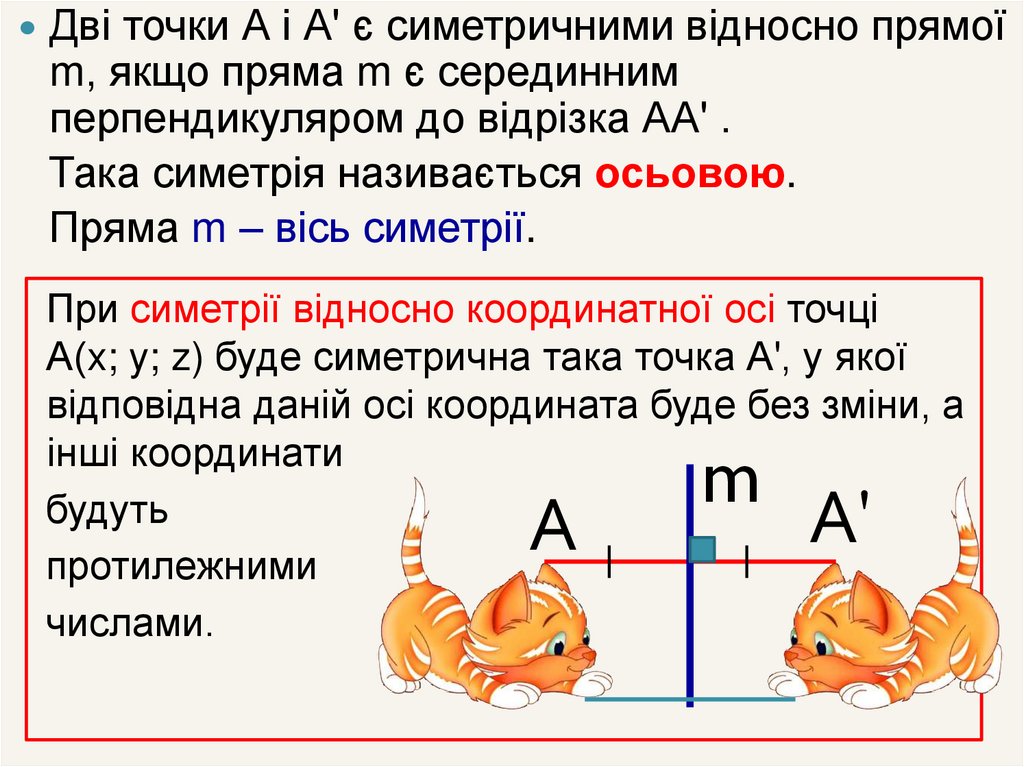
Дві точки А і А' є симетричними відносно прямоїm, якщо пряма m є серединним
перпендикуляром до відрізка АА' .
Така симетрія називається осьовою.
Пряма m – вісь симетрії.
При симетрії відносно координатної осі точці
А(x; y; z) буде симетрична така точка А', у якої
відповідна даній осі координата буде без зміни, а
інші координати
будуть
протилежними
числами.
А
m
А'
13.
Дві точки А і А' є симетричними відносно площини β,якщо ця площина є перпендикулярною до відрізка
АА' і ділить його навпіл.
Така симетрія називається дзеркальною.
Площина β – площина симетрії.
При симетрії відносно координатної
площини точці А(x; y; z) буде
симетрична така точка,
у якої відповідні
даній площині
координати будуть
без зміни, а інша
– з протилежним
знаком.
А
β
А'
14.
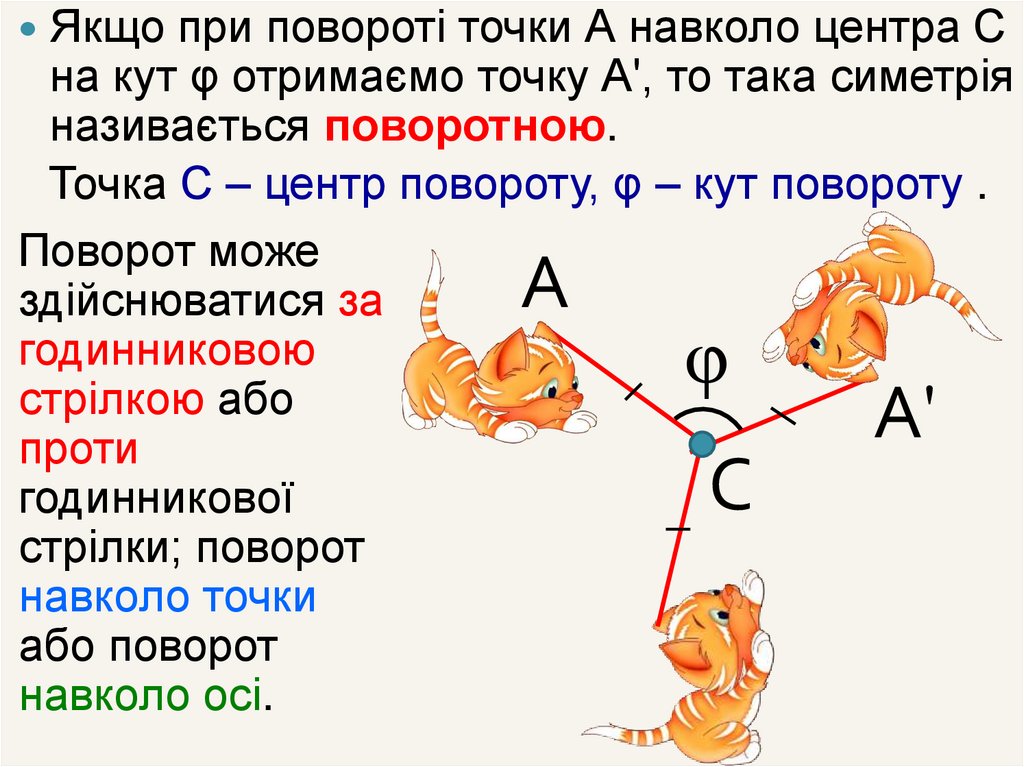
Якщо при повороті точки А навколо центра Сна кут φ отримаємо точку А', то така симетрія
називається поворотною.
Точка С – центр повороту, φ – кут повороту .
Поворот може
здійснюватися за
годинниковою
стрілкою або
проти
годинникової
стрілки; поворот
навколо точки
або поворот
навколо осі.
А
φ
С
А'
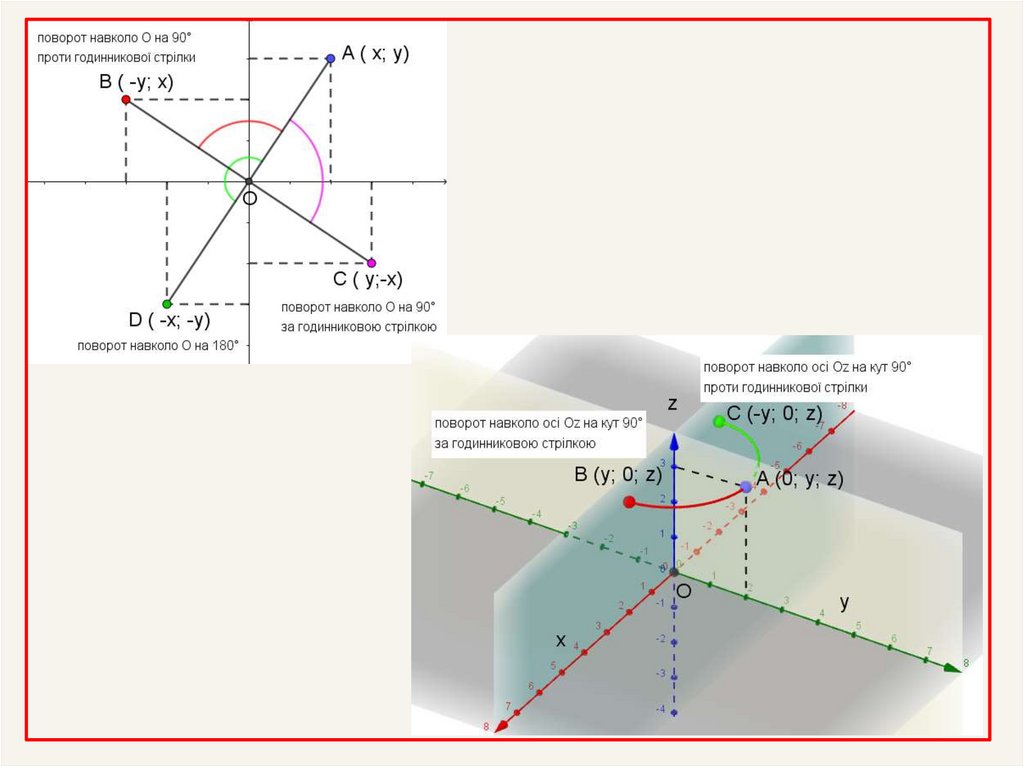
15.
16.
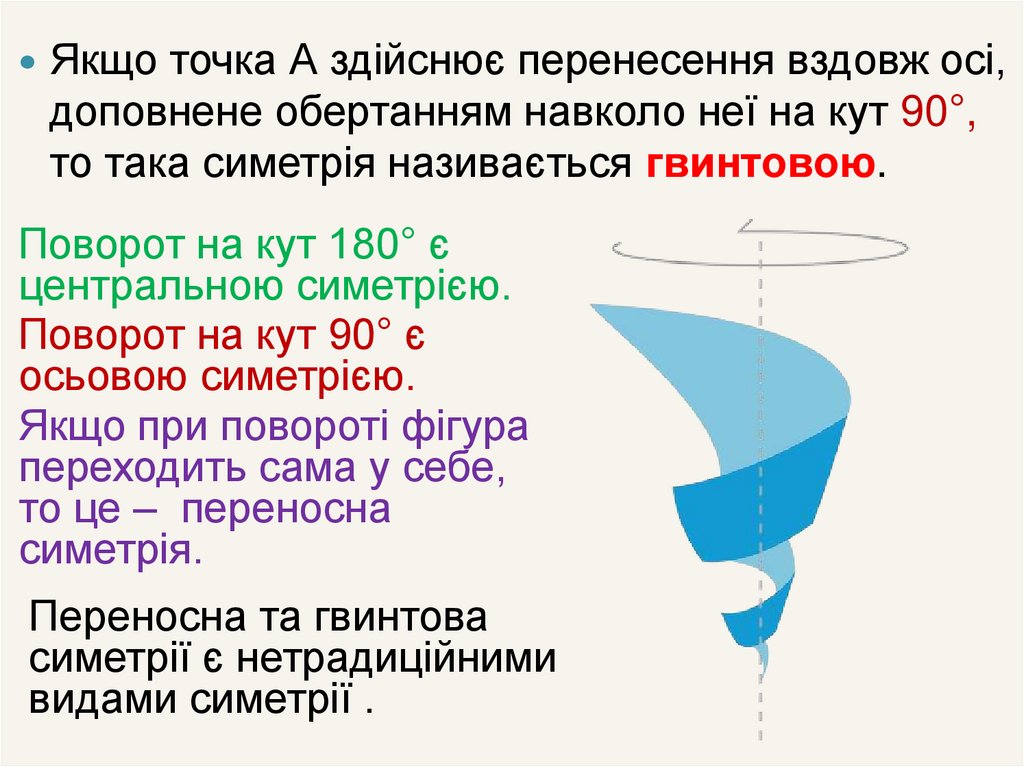
Якщо точка А здійснює перенесення вздовж осі,доповнене обертанням навколо неї на кут 90°,
то така симетрія називається гвинтовою.
Поворот на кут 180° є
центральною симетрією.
Поворот на кут 90° є
осьовою симетрією.
Якщо при повороті фігура
переходить сама у себе,
то це – переносна
симетрія.
Переносна та гвинтова
симетрії є нетрадиційними
видами симетрії .
17. Проект учнів 10 класу “Симетрія у навколишньому світі”
18. Симетрія у математиці
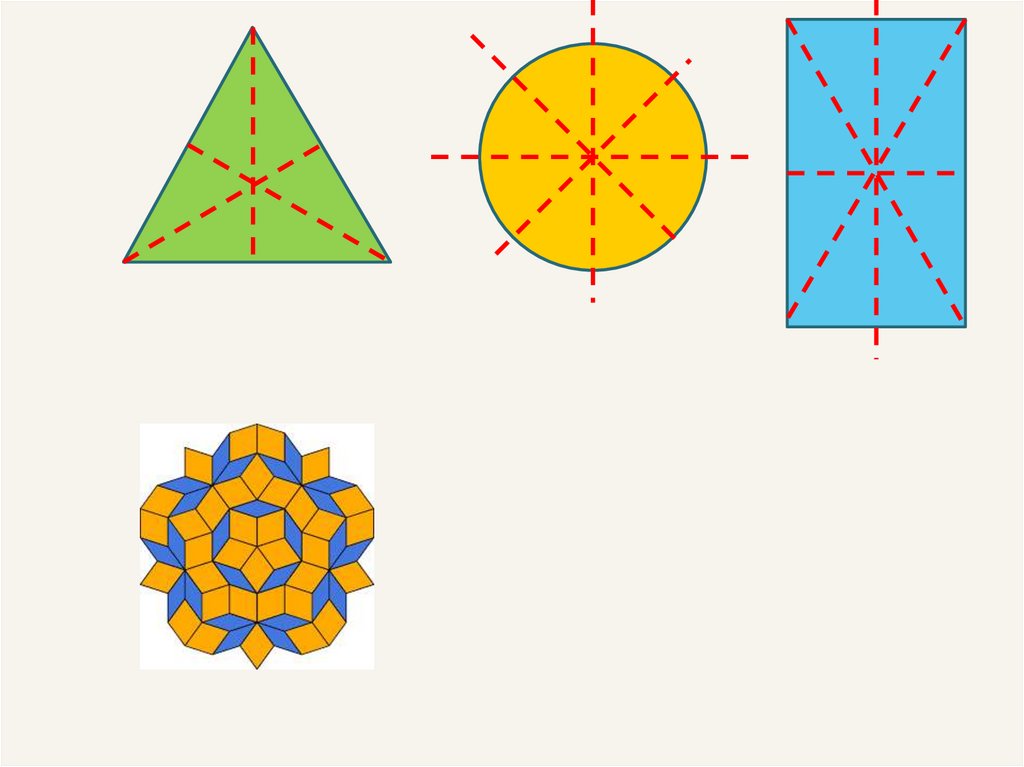
19.
У математиці багато фігур і цифр мають осьову(горизонтальну чи вертикальну) або дзеркальну
симетрію.
20.
21.
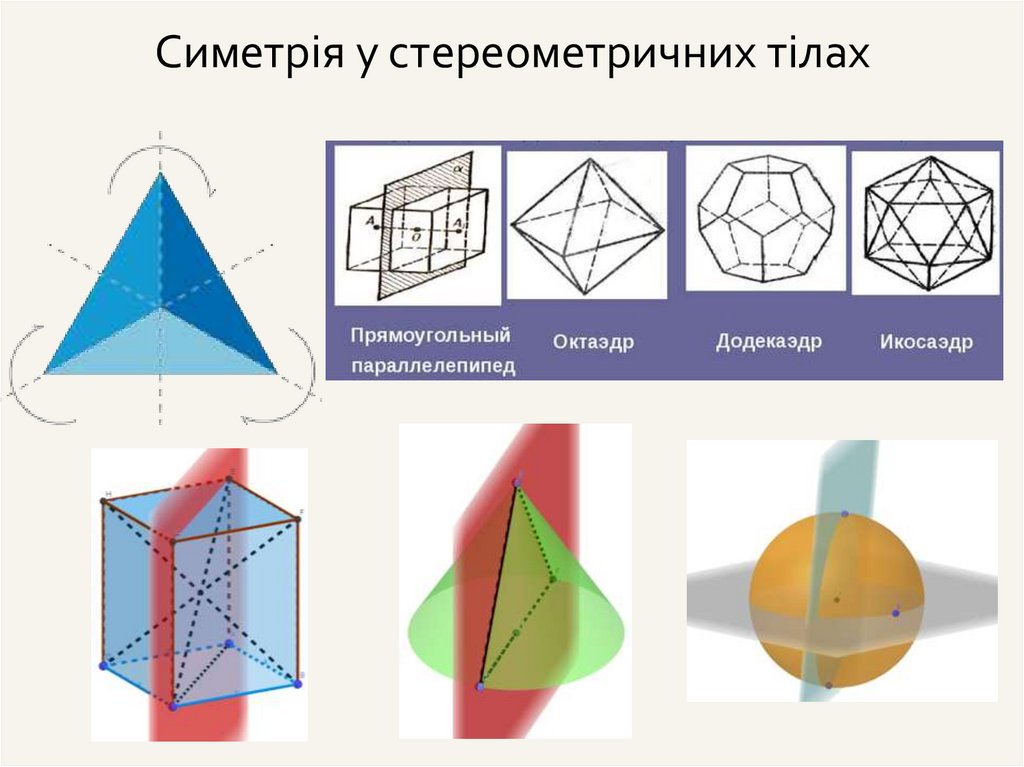
Симетрія у стереометричних тілах22.
23.
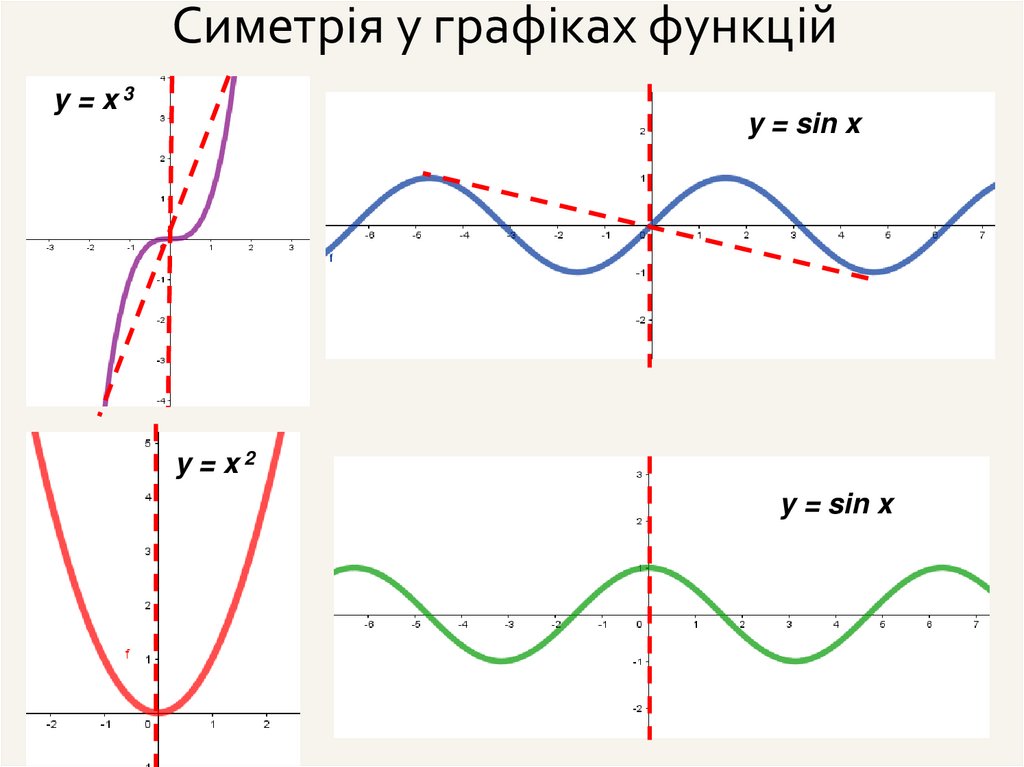
Симетрія у графіках функційy = x3
y = sin x
y = x2
y = sin x
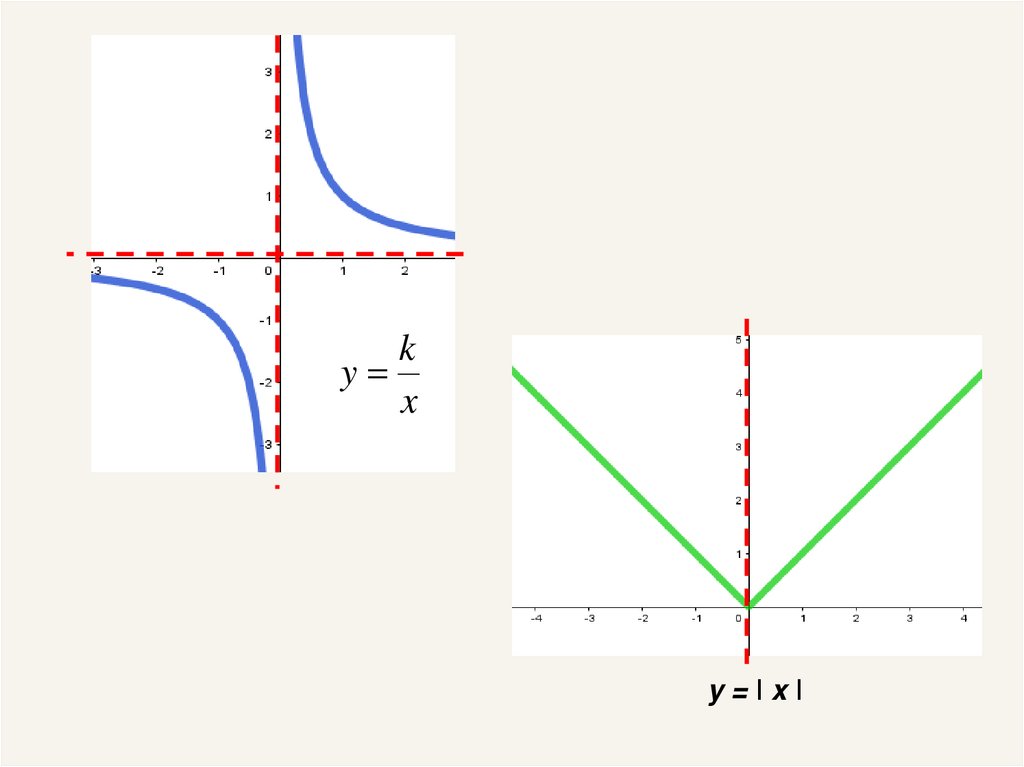
24.
ky
x
y=ǀxǀ
25. Симетрія у біології
26.
У живій і неживій природі симетрія зустрічається дуже часто.Це зумовлено способом існування – несиметричні комахи і
птахи не змогли б літати, листочки у рослинах затіняли б одне
одного.
Центральна
і
поворотна
симетрії
Медуза
Аденовірус
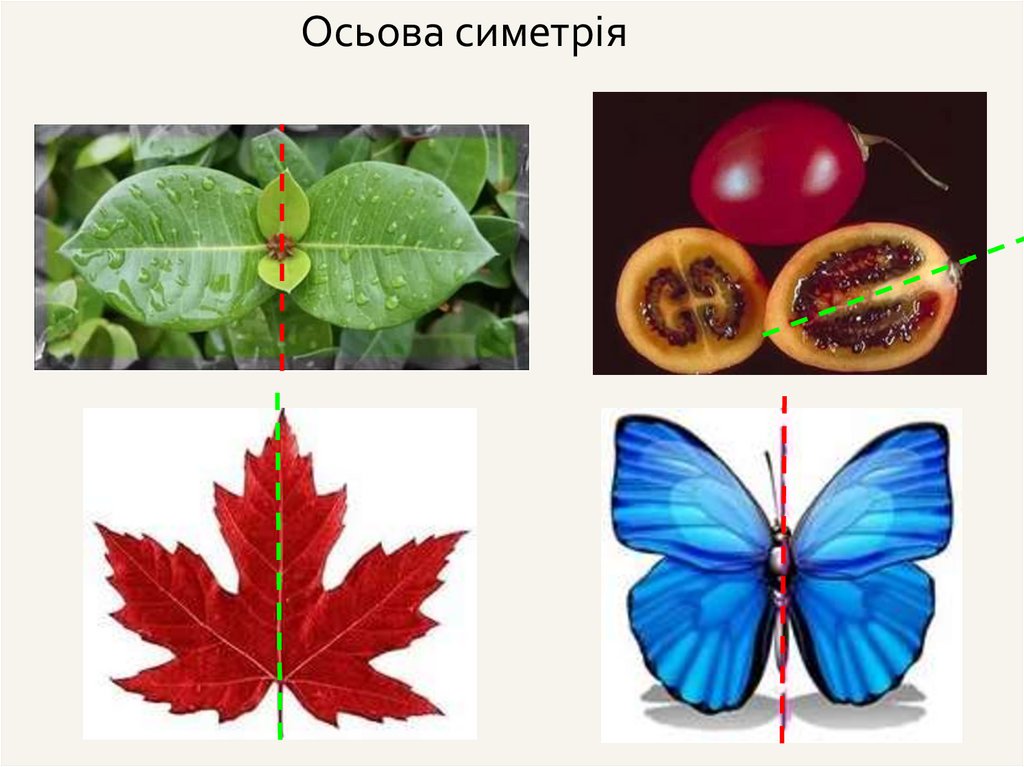
27.
Осьова симетрія28.
Дзеркальнасиметрія
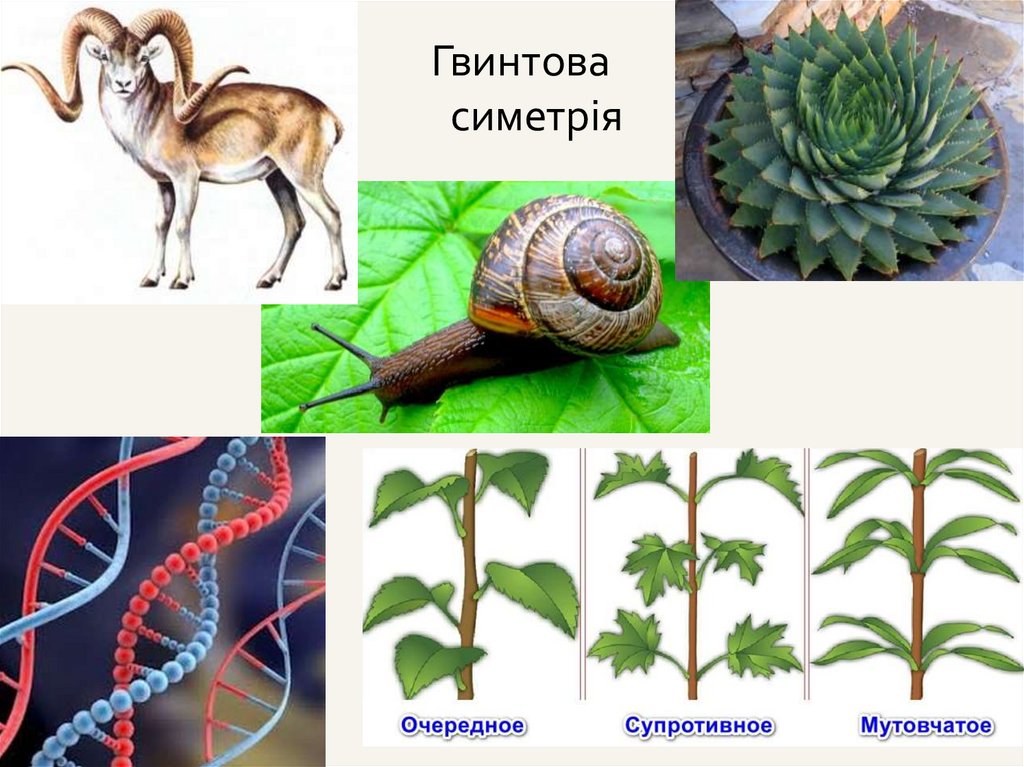
29.
Гвинтовасиметрія
30.
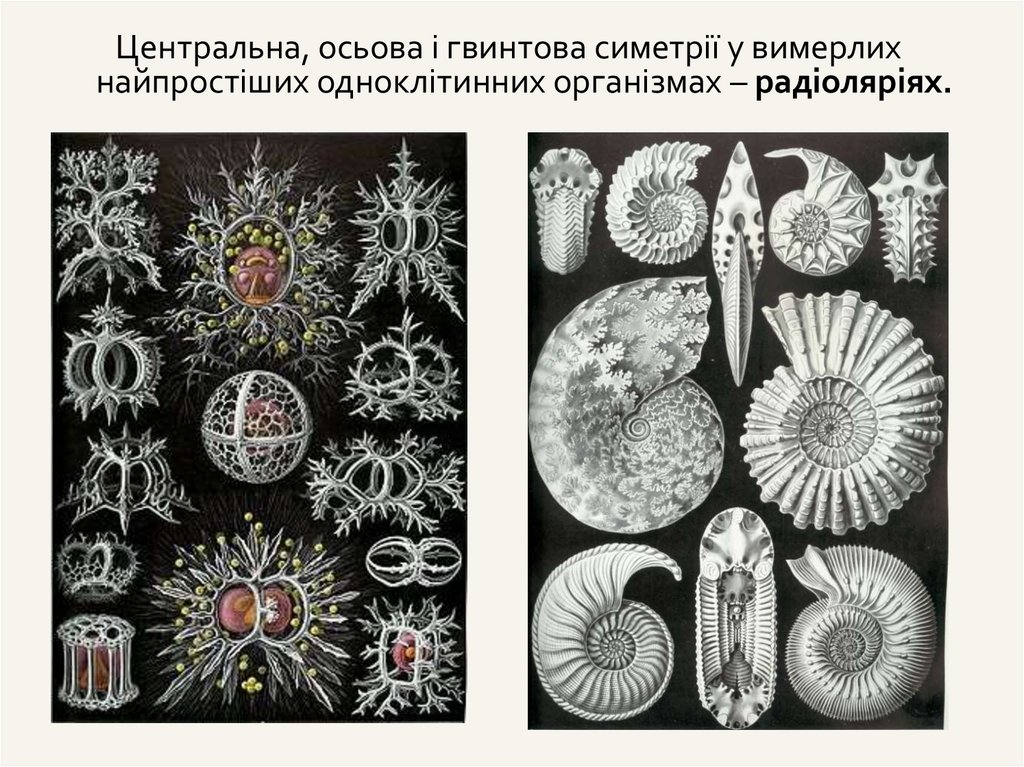
Центральна, осьова і гвинтова симетрії у вимерлихнайпростіших одноклітинних організмах – радіоляріях.
31.
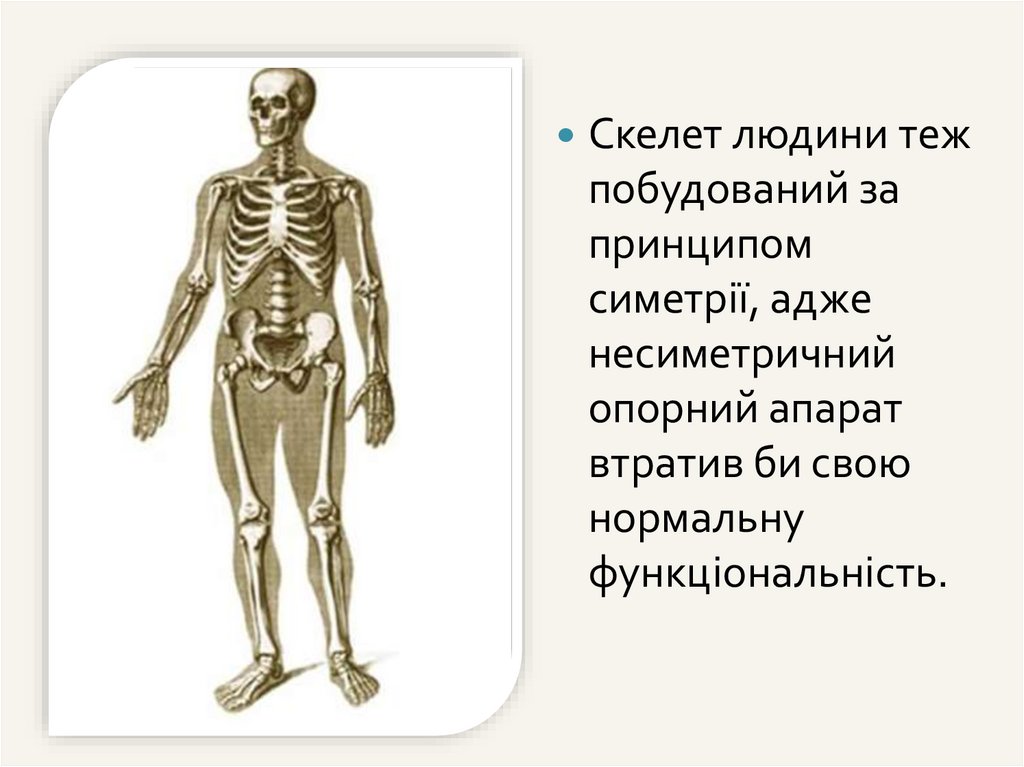
Скелет людини тежпобудований за
принципом
симетрії, адже
несиметричний
опорний апарат
втратив би свою
нормальну
функціональність.
32. Симетрія у хімії
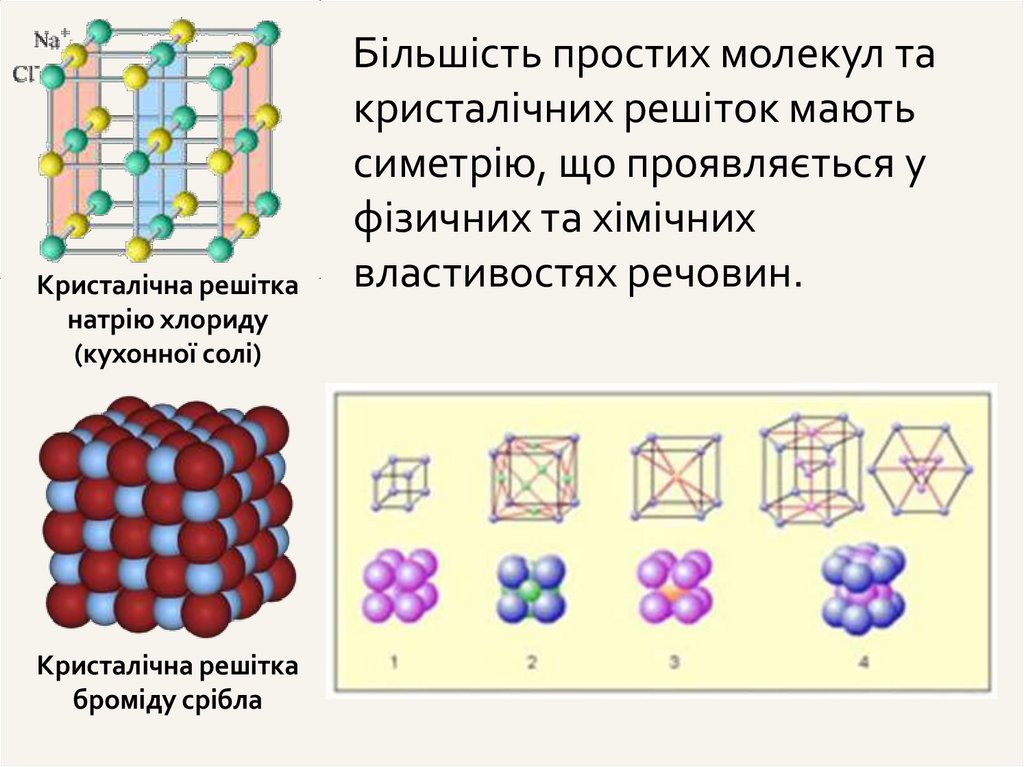
33.
Кристалічна решітканатрію хлориду
(кухонної солі)
Кристалічна решітка
броміду срібла
Більшість простих молекул та
кристалічних решіток мають
симетрію, що проявляється у
фізичних та хімічних
властивостях речовин.
34.
Симетрія многогранників яскраво проявляється уструктурі мінералів
35.
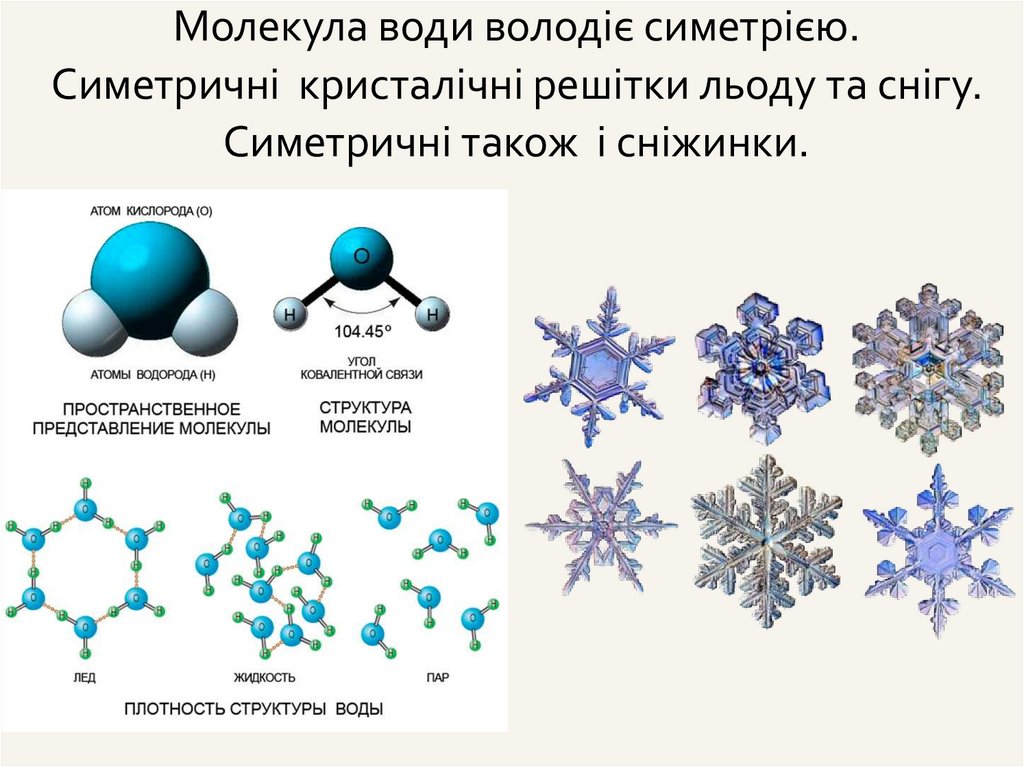
Молекула води володіє симетрією.Симетричні кристалічні решітки льоду та снігу.
Симетричні також і сніжинки.
36. Симетрія у фізиці і техніці
37.
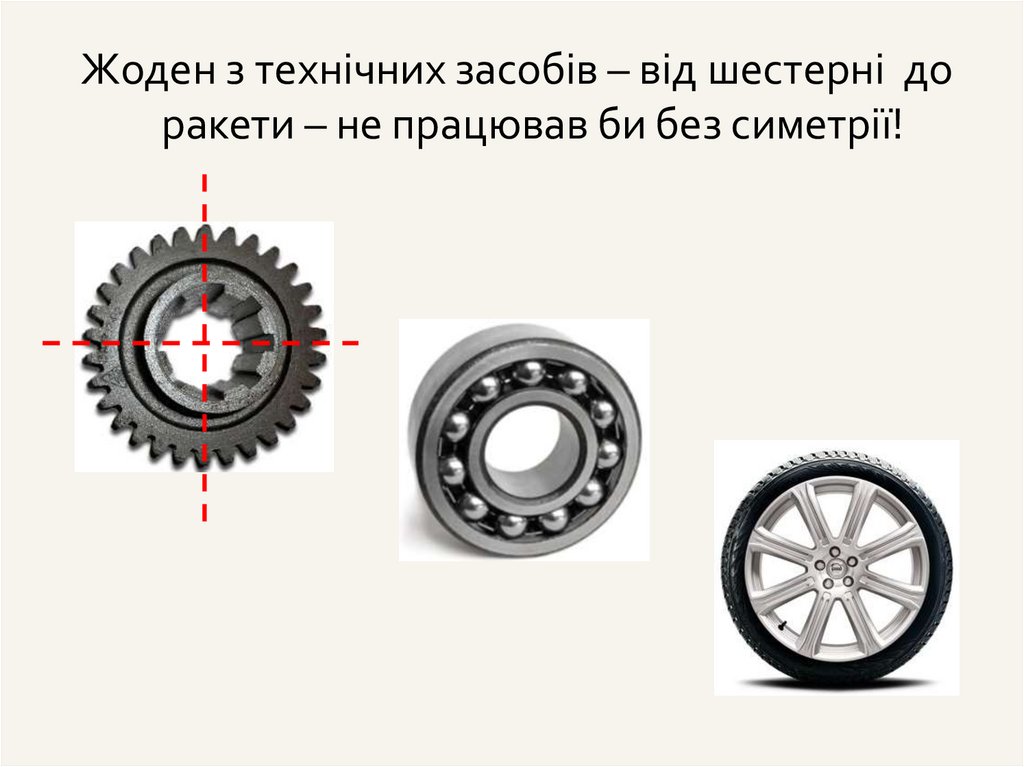
Жоден з технічних засобів – від шестерні доракети – не працював би без симетрії!
38.
39.
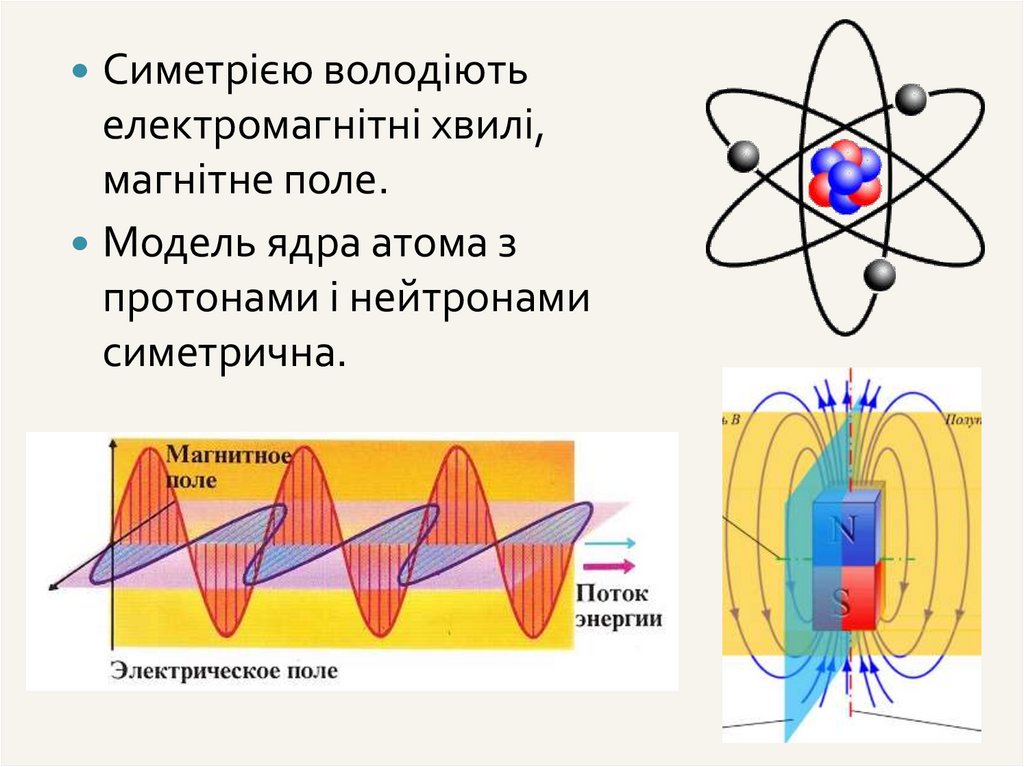
Симетрією володіютьелектромагнітні хвилі,
магнітне поле.
Модель ядра атома з
протонами і нейтронами
симетрична.
40.
Галактика Молочний шляхНайстаріша галактика А1689В11.
Їй 2,6 млдр.років
Галактики і квазари мають
симетричну будову.
Магнітне поле Землі теж
симетричне відносно полюсів.
Квазари
41. Симетрія в архітектурі
42.
Вибираючи симетричніформи, архітектори
прагнули досягти
природної гармонії ,
як ознаки стійкості та
рівноваги.
Тадж-Махал, Індія
Пантеон
Собор Паризької Богоматері
43.
Храм Лотоса в ІндіїБашти
Петронаса
у Малайзії
Ейфелева вежа у Парижі,
Франція
44.
Прикладвикористання
симетрії у
садовопарковому
мистецтві –
топіарії.
45.
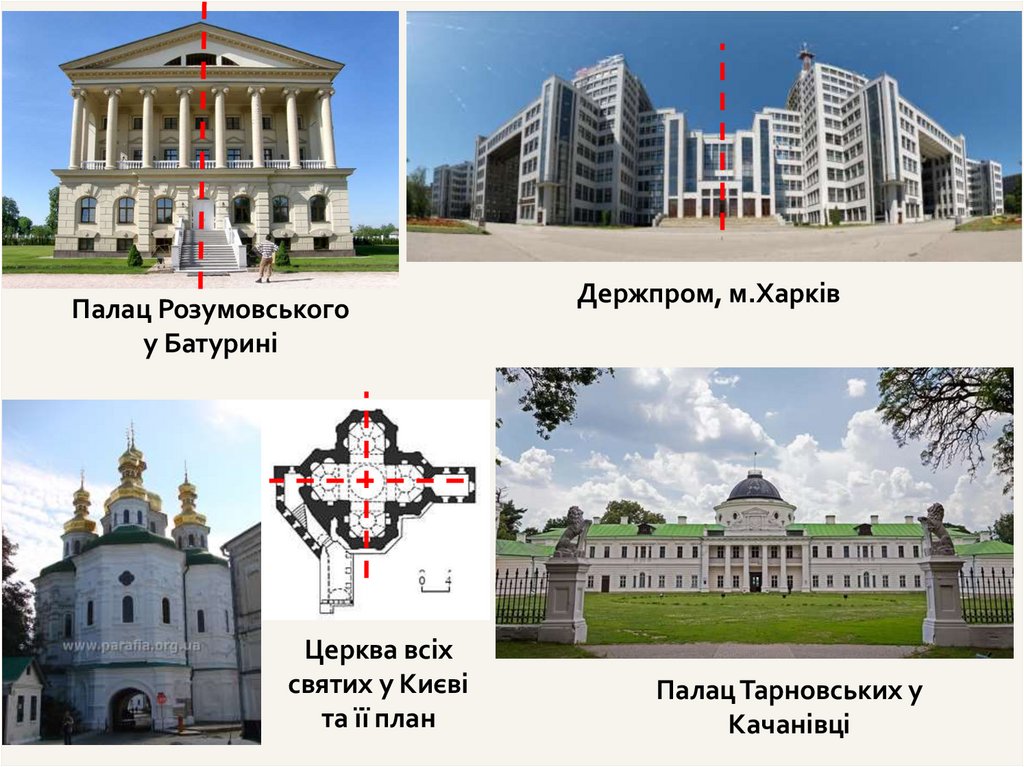
Палац Розумовськогоу Батурині
Церква всіх
святих у Києві
та її план
Держпром, м.Харків
Палац Тарновських у
Качанівці
46.
47.
48. Симетрія у мистецтві і побуті
49.
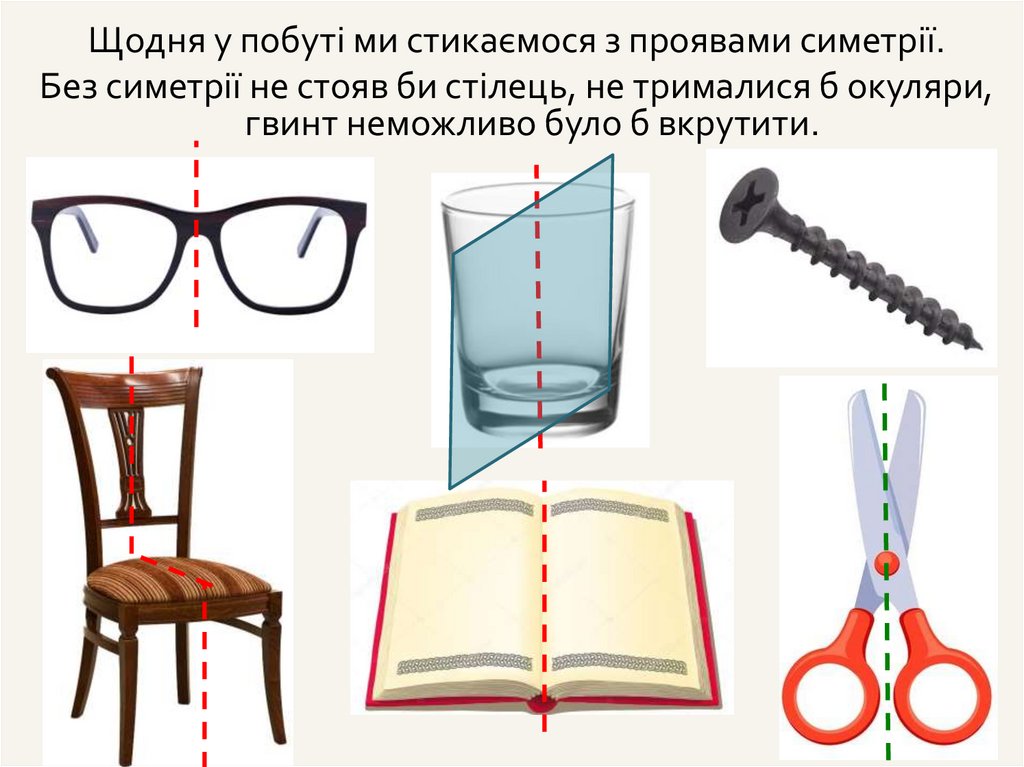
Щодня у побуті ми стикаємося з проявами симетрії.Без симетрії не стояв би стілець, не трималися б окуляри,
гвинт неможливо було б вкрутити.
50.
Килими, мереживо,витинанки, розписи на
стінах та декоративному
посуді, прикраси – це теж
прояв досконалості через
симетрію.
51.
52.
Симетрія в українській вишивці53. Симетрія в філології
54.
Симетрія літер55.
Амбіграма (від лат. ambi— «подвійний», і грец.
gramma — «буква») —
каліграфічний візерунок,
що дозволяє поєднати
два різні прочитання з
одного і того ж набору
ліній.
56.
57.
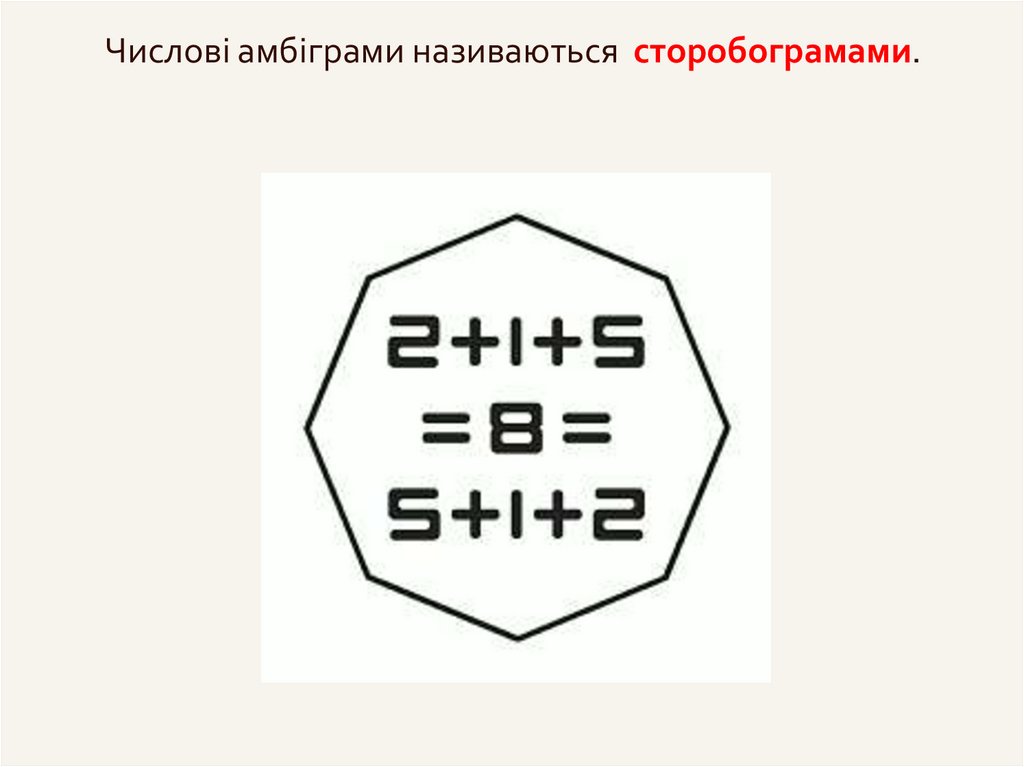
Числові амбіграми називаються сторобограмами.58.
Літературним праобразом амбіграм можна вважатипаліндроми — слова або фрази, які читаються однаково
як зліва направо, так і справа наліво.
59. Симетрія у історії
60.
Пізнавальну силу симетрії оцінилифілософи Стародавньої Греції,
використовуючи її в своїх теоріях.
Так, наприкфілософськихлад,
Анаксимандр з Мілета, який жив у
першій половині VI ст. до н. е.,
використовував симетрію в своїй
космологічної теорії, де в центрі світу
помістив Землю - головне, на його
думку, тіло світу. Вона повинна була
мати досконалу, симетричну форму,
форму циліндра, а на периферії
обертаються величезні вогняні
кільця, закриті повітряними хмарами і
дірками, які і здаються нам зірками.
Земля розташована точно в центрі, і
тут симетрія має сенс рівноваги.
61.
Емпедокл вважав Всесвітсферою - втіленням гармонії і
спокою. Сферос - величезний
однорідний шар, породження
двох протилежних стихій Любові і ворожнечі. Перша
стихія з'єднує, друга - роз'єднує.
Їх гармонія - симетрія призводить до стійкого,
циклічного рівноваги світу Сферос. Переважання однієї чи
іншої стихією - асиметрія призводить до циклічного ходу
світового процесу.
62.
Ідею симетрії використовувалиЛевкіпп і Демокріт. За їх вченням,
світ складається з порожнечі і атомів,
з яких побудовані всі тіла і душі.
Таким чином, стародавнє мистецтво
використовувало просторову
симетрію.
Гармонія (симетрія) складається з
протилежностей. В просторової
симетрії протилежності явно видно.
Наприклад, права і ліва кисті рук
людини. Таких протилежностей
стародавні вчені нарахували десять
пар, наприклад, парне - непарне,
пряме - криве, праве - ліве і т.д.
Левкіпп
Демокріт
63.
Леонардо да Вінчі не оминув своєю увагою і симетрію. Вінрозглянув рівновагу кулі, що має опору в центрі ваги: дві
симетричні половини кулі врівноважують одна одну, і куля не
падає.
Як художник він головну увагу приділяв вивченню законів
перспективи і пропорцій, за допомогою яких виявляються
художні достоїнства творів мистецтва.
64.
У науку симетрія увійшла в 30-хрр. XIX ст. в зв'язку з відкриттям
Гесселем 32 кристалографічних
класів і появою теорії груп як
області чистої математики.
Кристали наділені найбільшою
величиною симетрії з усіх
реальних об'єктів, вони блищать
своєю симетрією. Кристали - це
симетричні тіла, структура яких
визначається періодичним
повторенням в трьох вимірах
елементарного атомного мотиву.
65.
Е. Галуа запропонувавкласифікувати алгебраїчні
рівняння за їх групами симетрії.
66.
Ф. Клейн запропонував взятиідею симетрії як єдиного
принципу при побудові різних
геометрій.
Клейн розвинув свою концепцію
у фізиці і механіці.
Програма Клейна як завдання
пошуку різних форм симетрії
виходить за рамки не тільки
геометрії, але і всієї математики в
цілому, перетворюється в
проблему пошуку єдиного
принципу для всього
природознавства.
67. Знання збираються по краплині, як вода в долині
Українське прислів’я68.
Закріплення новогоматеріалу
69.
Групова робота іззавданнями
70.
№1Запишіть координати точок, симетричних
точці А (3;– 4; 1) відносно:
1) Початку координат
(– 3; 4; – 1)
2) Площини xy ( 3;– 4; – 1)
3) Площини xz ( 3; 4; 1)
4) Осі Oz
(– 3; 4; 1)
71.
№2Точки А (5;– 3; 4) та В (– 3; 1; – 2) симетричні
відносно точки С. Які її координати?
Розв’язання:
За означенням центральної симетрії точка
С – середина відрізка АВ. Тоді:
5 ( 3 )
xc =
= 1;
2
4 ( 2 )
zc =
=
1;
2
Відповідь: С ( 1;– 1; 1)
3 1
уc =
= –1;
2
72.
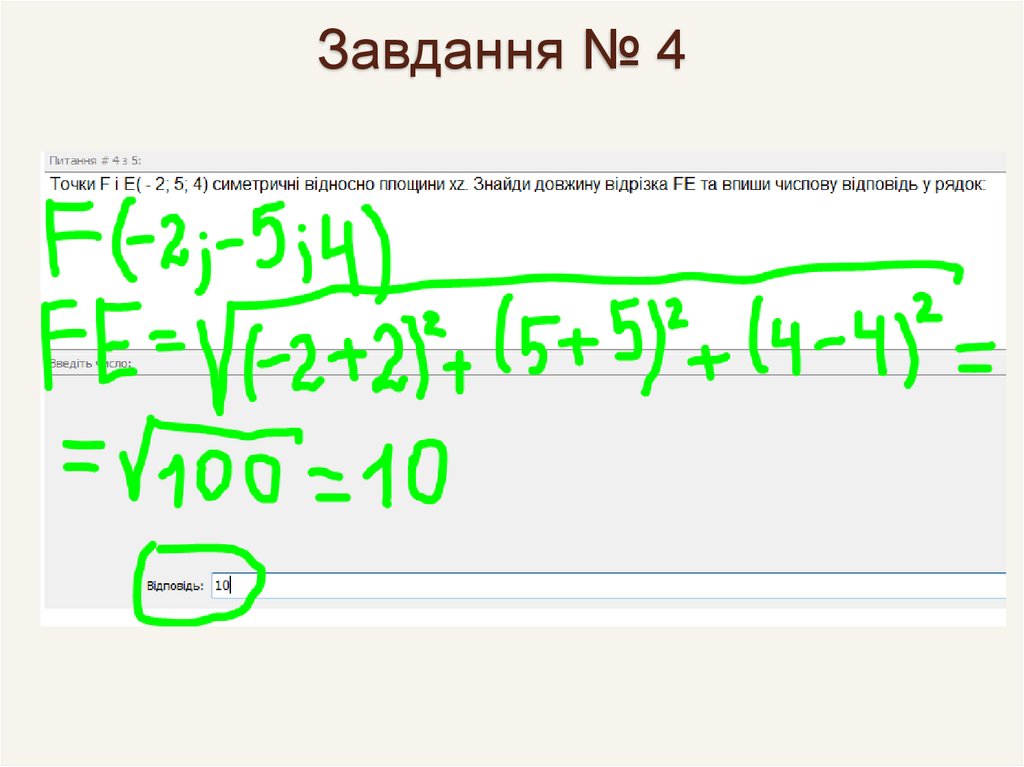
№3Точки E (– 3; 8; 7) та F симетричні відносно
площини ху. Знайдіть довжину відрізка EF.
Розв’язання:
За властивістю дзеркальної симетрії
будуть такі координати точки F :
(– 3; 8; –7).
Тоді за формулою довжини відрізка
маємо:
2
2
2
EF = ( 3 ( 3 )) ( 8 8 ) ( 7 7 ) =
= 196 14
Відповідь: EF = 14.
73.
Роботау динамічному середовищі
74.
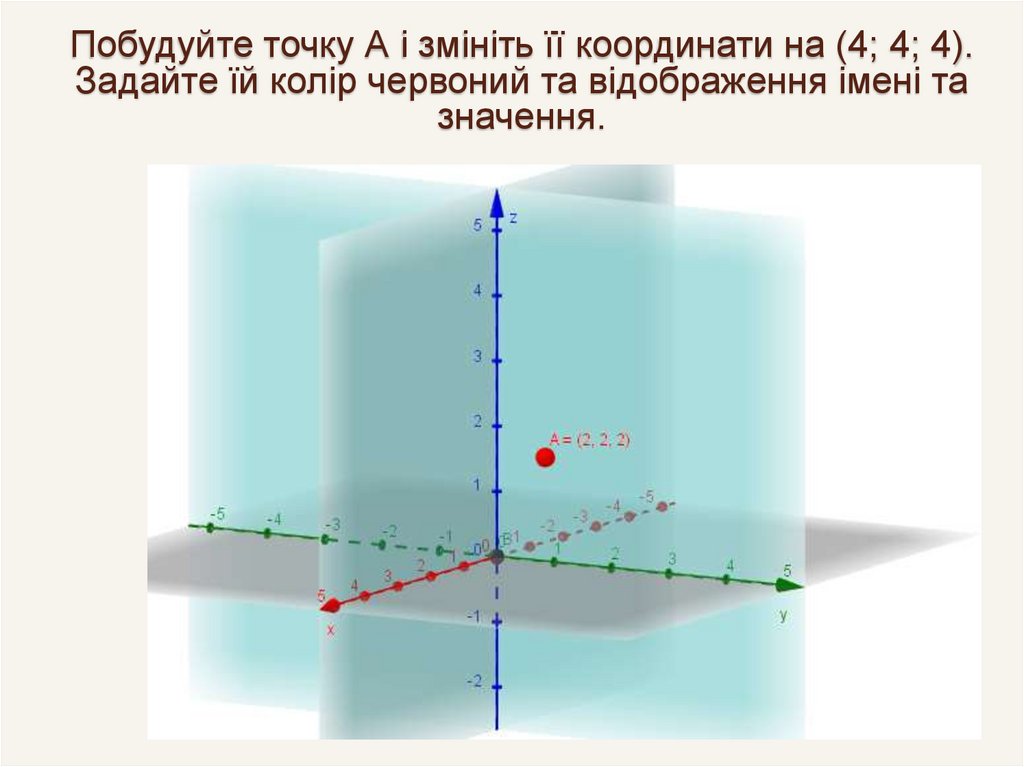
Побудуйте точку А і змініть її координати на (4; 4; 4).Задайте їй колір червоний та відображення імені та
значення.
75.
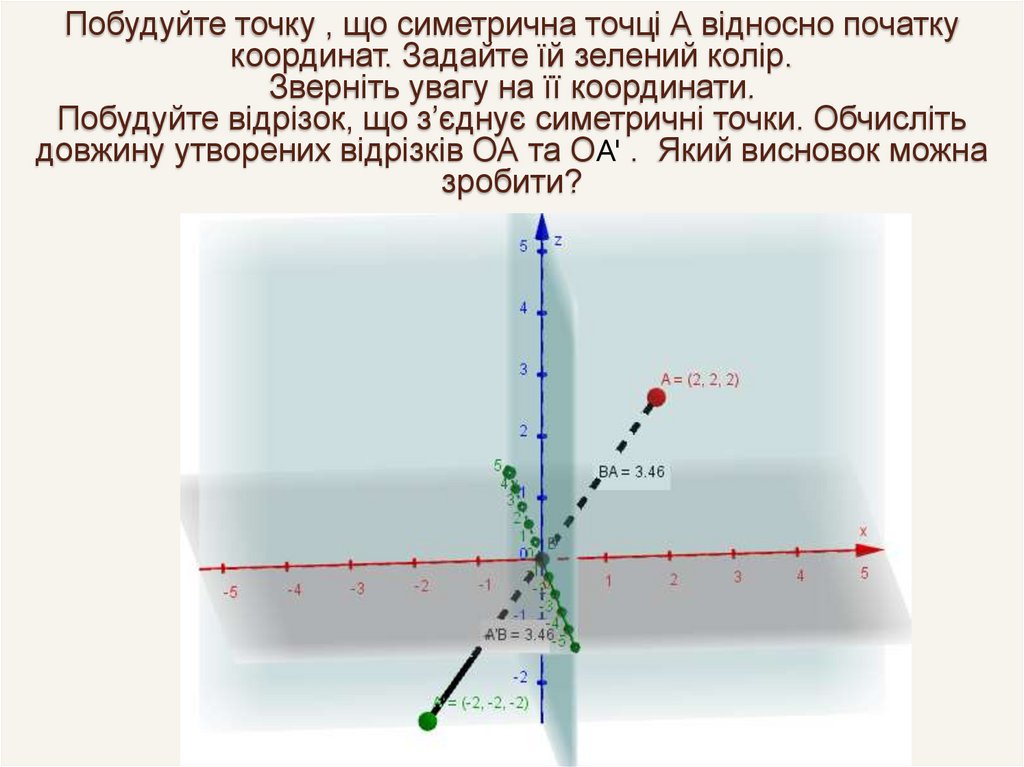
Побудуйте точку , що симетрична точці А відносно початкукоординат. Задайте їй зелений колір.
Зверніть увагу на її координати.
Побудуйте відрізок, що з’єднує симетричні точки. Обчисліть
довжину утворених відрізків ОА та ОА' . Який висновок можна
зробити?
76.
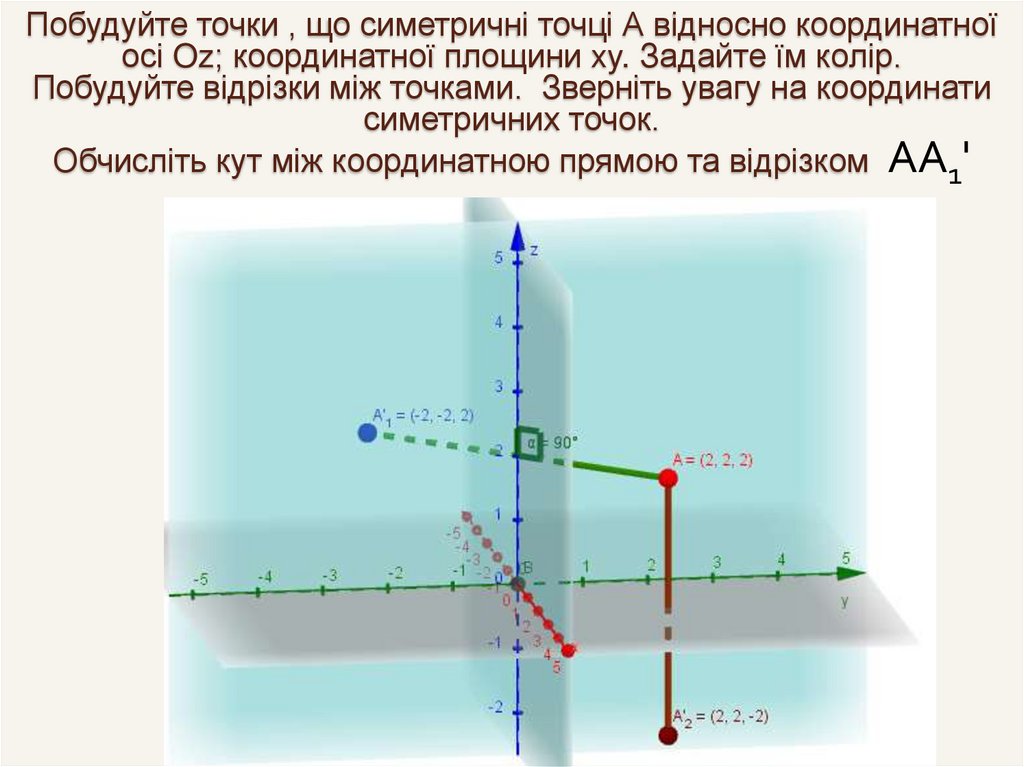
Побудуйте точки , що симетричні точці А відносно координатноїосі Oz; координатної площини xy. Задайте їм колір.
Побудуйте відрізки між точками. Зверніть увагу на координати
симетричних точок.
Обчисліть кут між координатною прямою та відрізком АА1'
77.
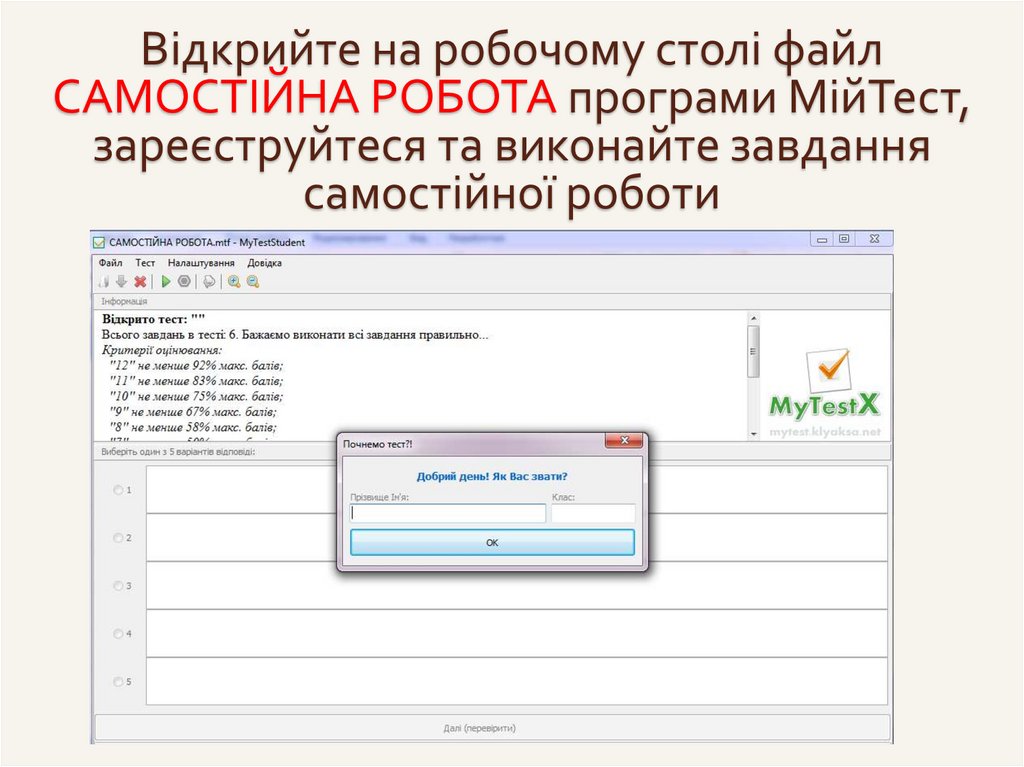
Самостійна робота78.
Відкрийте на робочому столі файлСАМОСТІЙНА РОБОТА програми МійТест,
зареєструйтеся та виконайте завдання
самостійної роботи
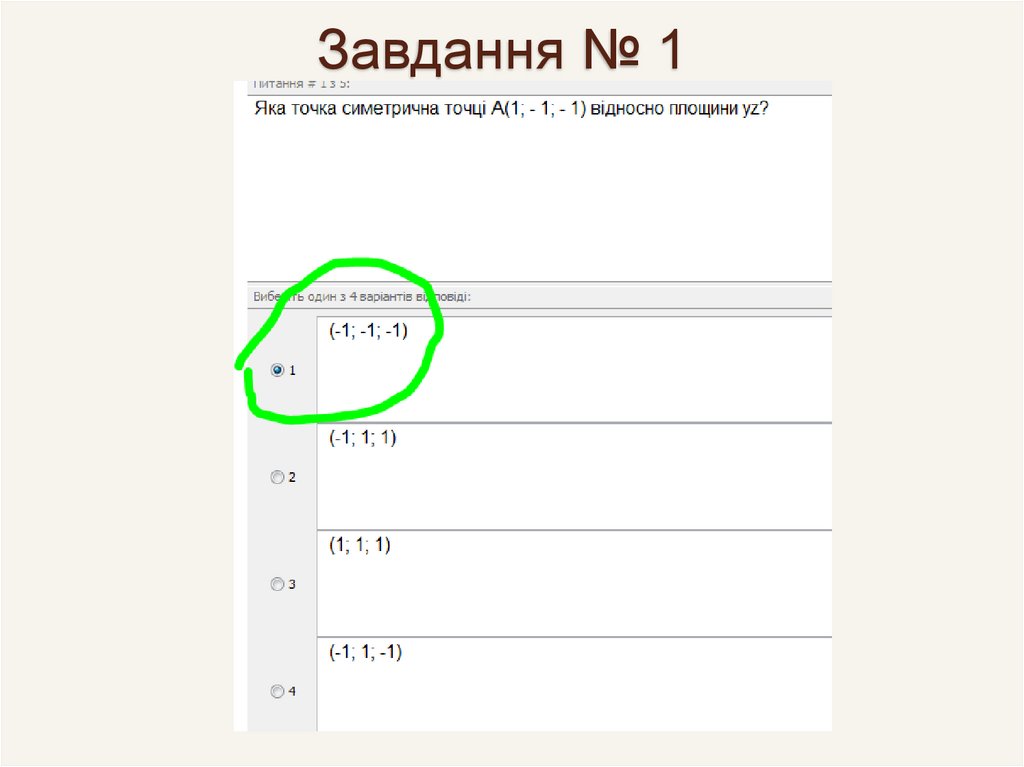
79. Завдання № 1
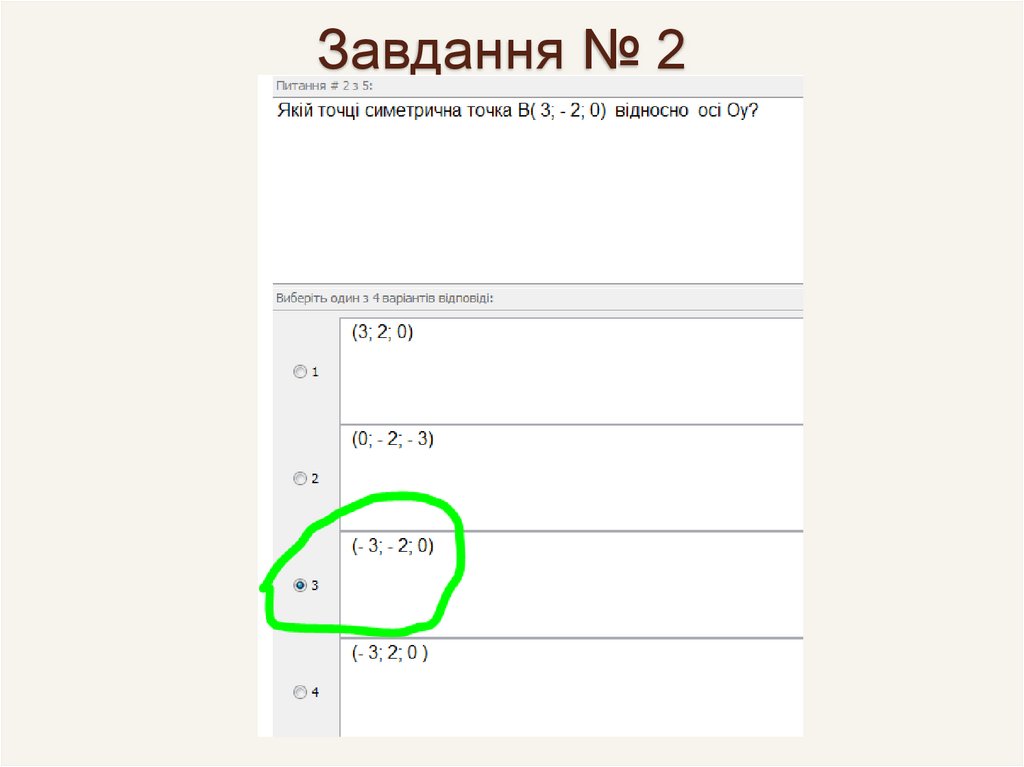
80. Завдання № 2
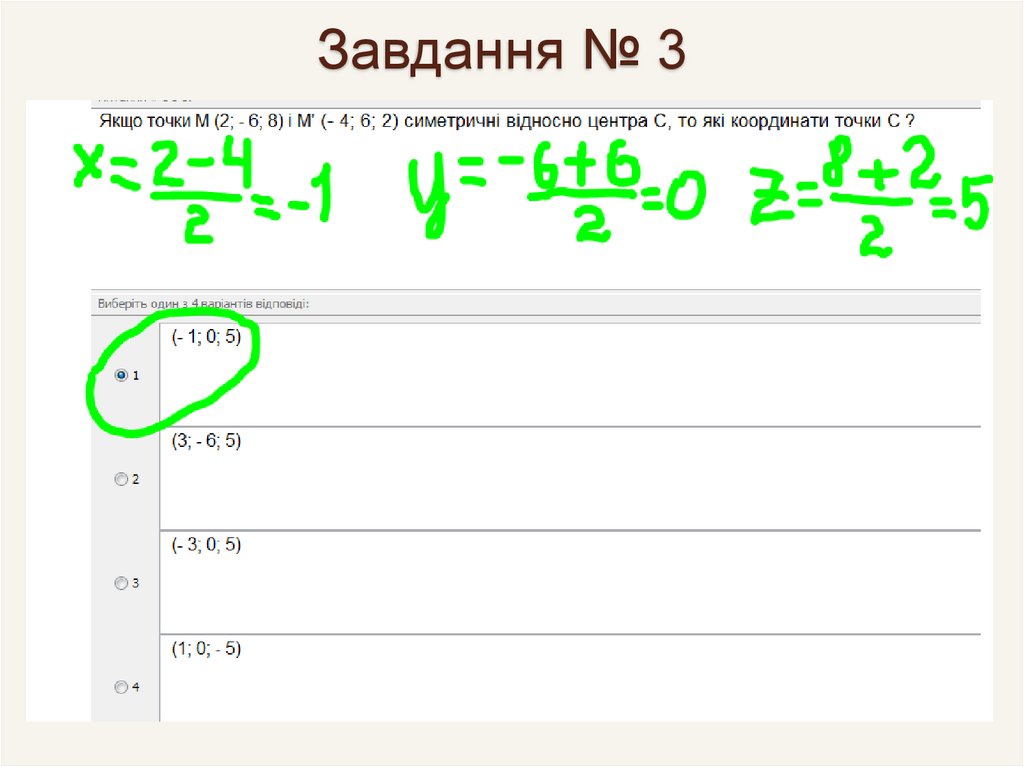
81. Завдання № 3
82. Завдання № 4
83. Завдання № 5
84.
Домашнє завданняБлог вчителя математики Кальченко
Вікторії Іванівни
https://sites.google.com/site/kalchenkovi78/
Домашнє завдання 10 клас Симетрія.docx
85.
Підсумки уроку86.
Визначення досягнутих завданьПоглибити знання про симетрію у просторі та її
властивості
Визначити, чи зустрічається симетрія у
навколишньому світі
Навчитися використовувати властивості
симетрії до розв’язування геометричних задач
Навчитися будувати симетричні фігури
Вияснити, чи міг би наш світ існувати без
симетрії повноцінно?
87.
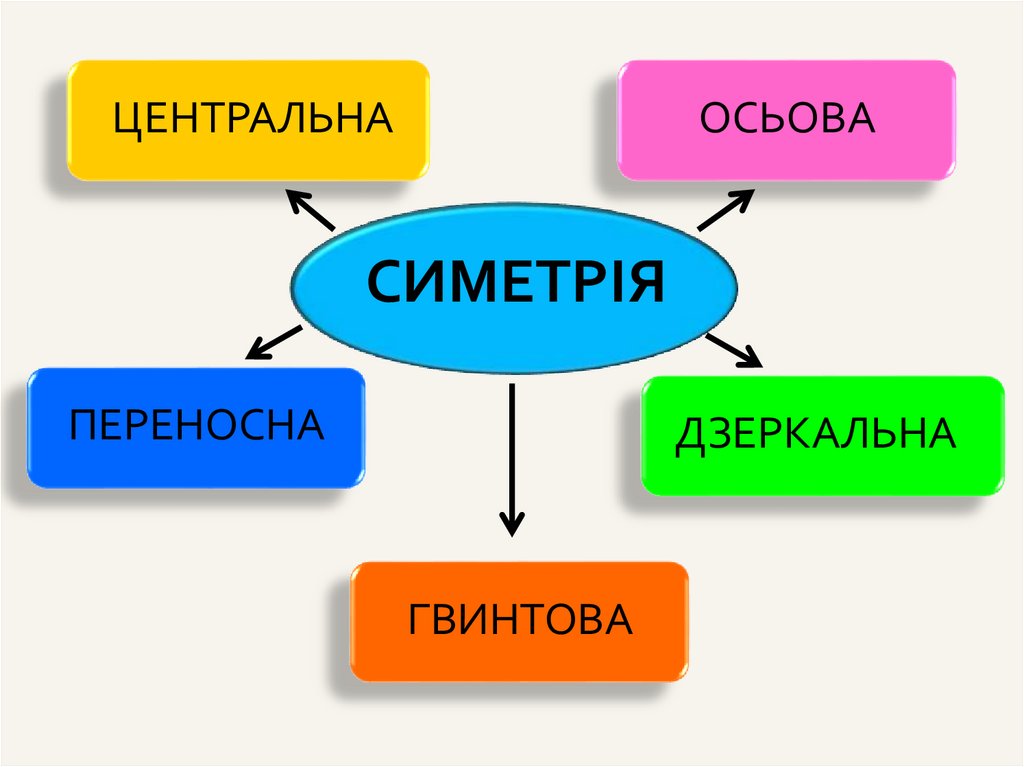
ЦЕНТРАЛЬНАОСЬОВА
СИМЕТРІЯ
ПЕРЕНОСНА
ДЗЕРКАЛЬНА
ГВИНТОВА
88.
Рефлексія89.
Встановіть цеглинку відповідного кольору у піраміду нату висоту, на якій тепер знаходяться ваші знання.
Зелену – задоволений, Червону – не задоволений
90.
Урок закінчено!Бажаю успіху у здобутті
нових знань!




























































 mathematics
mathematics








