Similar presentations:
Знакопостоянные ряды
1.
Знакопостоянные рядыМатематический анализ.
Дифференциальные и разностные уравнения
Раздел 2. Ряды.
Микротема 3-1 Знакопостоянные ряды
к.ф.-м.н. Шуклина Анна Фаридовна
ЧелГУ, ИИТ
2016
Шуклина А.Ф.
Микротема 3-1
2.
Знакопостоянные рядыПосле изучения данной микротемы вы должны:
знать понятие числового ряда;
знать понятия частичной суммы ряда;
уметь применять необходимый признак сходимости числовых рядов;
уметь применять признаки Даламбера, Коши и сравнения.
Шуклина А.Ф.
Микротема 3-1
3.
Знакопостоянные рядыПризнаки сходимости
Определение
Пусть задана последовательность действительных чисел un , n = 1, 2, . . ., составим
новую последовательность Sn , n = 1, 2, . . .
S1 = u1
S2 = u1 + u2
...
Sn = u1 + u2 + . . . + un .
Сумма вида u1 + u2 + . . . + un + . . . называется числовым рядом с общим членом
un и обозначается
∞
X
un ,
(1)
n=1
элементы un – члены ряда, а последовательность {Sn } – последовательность
частичных сумм ряда, Sn – n-я частичная сумма ряда.
Шуклина А.Ф.
Микротема 3-1
4.
Знакопостоянные рядыПризнаки сходимости
Определение
Если последовательность частичных сумм ряда (1) сходится, то он называется
сходящимся рядом, а если расходится – расходящимся.
Определение
Если (1) сходится, то lim Sn = S называют суммой ряда.
n→∞
Определение
Суммой рядов
∞
P
n=1
an и
∞
P
bn называется ряд вида
n=1
∞
P
(an + bn ), т.е. члены нового
n=1
ряда образованы как суммы соответствующих членов данных рядов .
Шуклина А.Ф.
Микротема 3-1
5.
Знакопостоянные рядыПризнаки сходимости
Свойства сходящихся рядов
∞
∞
P
P
1 Если
an – сходится, то ряд
C · an сходится и
n=1
n=1
∞
X
C · an = C ·
n=1
2
Если
∞
P
n=1
an и
∞
P
bn сходятся, то
n=1
∞
X
an
n=1
∞
P
(an + bn ) сходится и
n=1
∞
X
(an + bn ) =
n=1
Шуклина А.Ф.
∞
X
n=1
an +
∞
X
n=1
Микротема 3-1
bn
6.
Знакопостоянные рядыПризнаки сходимости
Доказательство.
Свойство 1.
∞
P
an сходится. Составим n−ю частичную сумму ряда
По условию ряд
n=1
An = a1 + a2 + . . . + an . Тогда lim An = A.
n→∞
∞
P
Составим n−ю частичную сумму ряда
C · an
n=1
Sn = ca1 + ca2 + . . . + can = c(a1 + a2 + . . . + an ) = cAn .
Тогда
lim Sn = lim cAn = c · lim An = c · A.
n→∞
Получили, что для ряда
∞
P
n→∞
n→∞
C · an существует конечный предел последовательности
n=1
его частичных сумм, следовательно ряд
∞
P
C · an сходится.
n=1
Шуклина А.Ф.
Микротема 3-1
7.
Знакопостоянные рядыПризнаки сходимости
Доказательство.
Свойство 2.
∞
∞
P
P
По условию ряды
an и
bn сходятся. Составим n−е частичные суммы рядов
n=1
n=1
An = a1 + a2 + . . . + an и Bn = b1 + b2 + . . . + bn . Тогда lim An = A и lim Bn = B.
n→∞
n→∞
∞
P
Составим n−ю частичную сумму ряда
(an + bn )
n=1
Sn = (a1 + b1 ) + (a2 + b2 ) + . . . + (an + bn ) =
= (a1 + a2 + . . . + an ) + (b1 + b2 + . . . + bn ) = An + Bn .
Тогда
lim Sn = lim (An + Bn ) = lim An + lim Bn = A + B.
n→∞
Получили, что для ряда
n→∞
∞
P
n→∞
n→∞
(an + bn ) существует конечный предел
n=1
последовательности его частичных сумм, следовательно ряд сходится.
Шуклина А.Ф.
Микротема 3-1
8.
Знакопостоянные рядыПример 1.a Найти сумму ряда
∞
P
n=1
Признаки сходимости
1
n(n+1) .
1
1
1
= −
n(n + 1)
n n+1
Sn =
1 1 1 1
1
1
− + − + ··· + −
1 2 2 3
n n+1
1
Sn = 1 −
n+1
1
lim 1 −
=1
n→∞
n+1
Шуклина А.Ф.
Микротема 3-1
9.
Знакопостоянные рядыПризнаки сходимости
Пример 1.b
∞
X
1
4k
k=0
Sn = 1 +
Sn =
1
1
1
+
+ ··· + n
4 42
4
1(1 −
a1 (1 − q n )
=
1−q
1−
S=
Шуклина А.Ф.
1
4n )
1
4
4
3
Микротема 3-1
10.
Знакопостоянные ряды∞
P
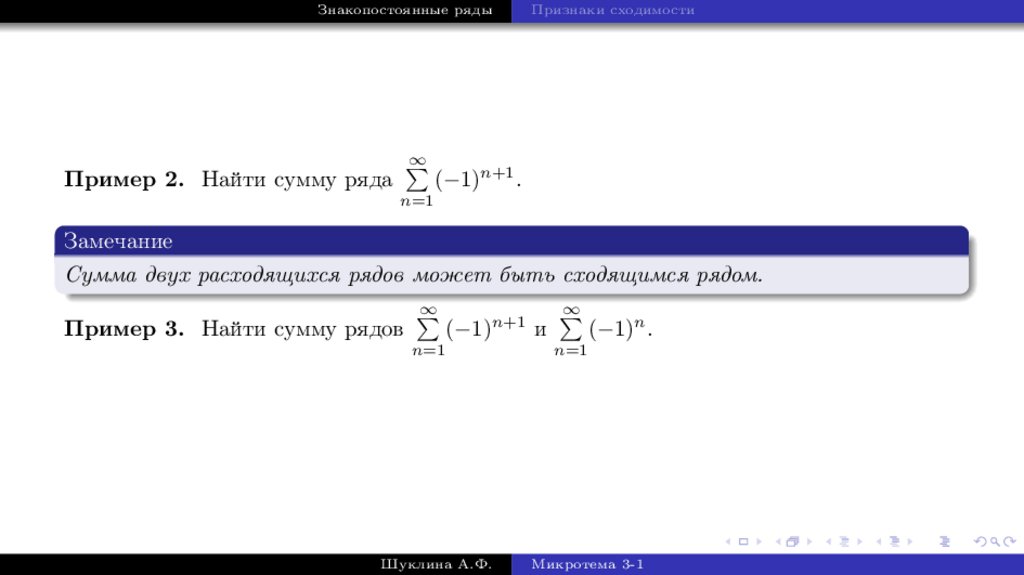
Пример 2. Найти сумму ряда
Признаки сходимости
(−1)n+1 .
n=1
Замечание
Сумма двух расходящихся рядов может быть сходящимся рядом.
Пример 3. Найти сумму рядов
∞
P
(−1)n+1 и
n=1
Шуклина А.Ф.
∞
P
(−1)n .
n=1
Микротема 3-1
11.
Знакопостоянные рядыПризнаки сходимости
Теорема
(Необходимое условие сходимости) Если ряд (1) сходится, то его общий член
стремится к нулю
lim un = 0.
n→∞
Замечание
Обратное неверно, то есть существуют ряды, для которых lim un = 0, но ряд
n→∞
расходится.
Следствие
Если предел общего члена ряда отличен от нуля или не существует, то ряд
расходится.
Шуклина А.Ф.
Микротема 3-1
(2)
12.
Знакопостоянные рядыПризнаки сходимости
Пример 1. Проверить необходимое условие и найти сумму ряда
∞
P
n=1
Пример 2. Проверить необходимое условие для следующих рядов
∞
X
n=1
n2
+1
2n2
n
∞
X
n
n+1
n=1
∞
X
3n
n2n
n=1
Шуклина А.Ф.
Микротема 3-1
√1 .
n
13.
Знакопостоянные рядыПризнаки сходимости
Теорема
Первый признак сравнения. Пусть дан ряд
∞
P
bn (3) и un ≤ bn , ∀n ∈ N. Тогда
n=1
1) если (3) сходится, то (1) сходится;
2) если (1) расходится, то (3) расходится.
Теорема
Второй признак сравнения. Если un ∼ bn , т.е. lim ubnn = k, то (1) и (3)
n→∞
сходятся или расходятся одновременно.
Гармонический ряд
∞
X
1
α
n
n=1
α>1
α≤1
Шуклина А.Ф.
⇒ ряд сходится,
⇒ ряд расходится.
Микротема 3-1
(4)
14.
Знакопостоянные рядыПризнаки сходимости
Теорема
Признак Даламбера Пусть дан ряд
∞
P
un . Тогда если существует число
n=1
q = lim
n→∞
un+1
un
(5)
и q > 1, то (1) расходится,
q < 1, то (1) сходится,
q = 1 – ? (вопрос остается открытым, данный признак нельзя применять к
исследованию данного ряда)
NB! Если общий член ряда содержит факториал, то рекомендуется применять для
исследования ряда на сходимость именно признак Даламбера.
Шуклина А.Ф.
Микротема 3-1
15.
Знакопостоянные рядыПризнаки сходимости
Теорема
Признак Коши (радикальный) Пусть дан ряд
число
√
q = lim n un
∞
P
un . Тогда если существует
n=1
n→∞
и q > 1, то (1) расходится,
q < 1, то (1) сходится,
q = 1 – ? (вопрос остается открытым, данный признак нельзя применять к
исследованию данного ряда)
Шуклина А.Ф.
Микротема 3-1
(6)
16.
Знакопостоянные рядыПризнаки сходимости
Пример 1. Исследовать на сходимость следующие ряды
a)
∞
∞
X
X
16
16
∼
2
n + 1 n=1 n2
n=1
Вывод: сходится по второму признаку сравнения, т.к. эквивалентен сходящемуся
обобщенному гармоническому ряду.
Шуклина А.Ф.
Микротема 3-1
17.
Знакопостоянные рядыПризнаки сходимости
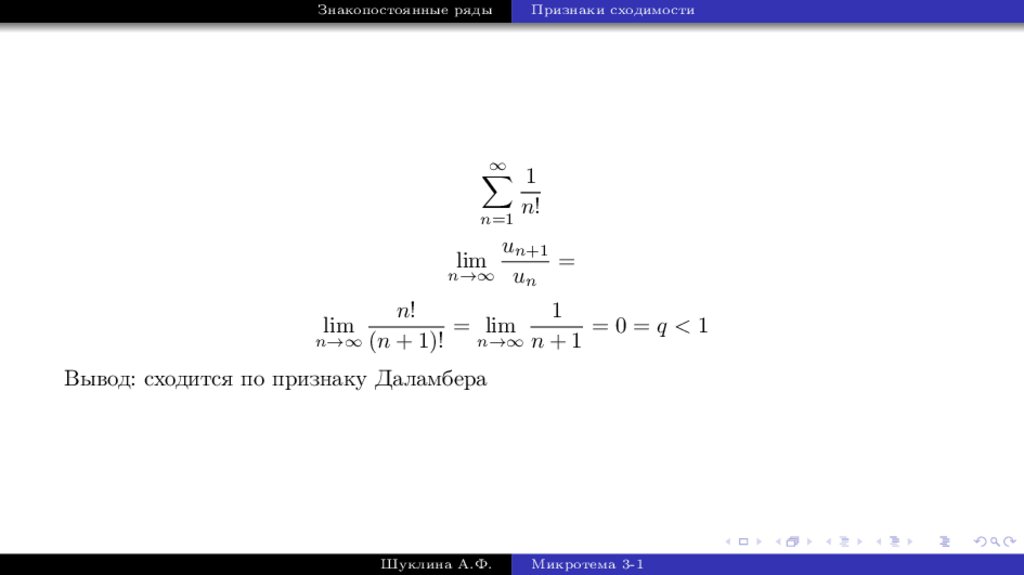
∞
X
1
n!
n=1
lim
n→∞
lim
n→∞
un+1
=
un
n!
1
= lim
=0=q<1
(n + 1)! n→∞ n + 1
Вывод: сходится по признаку Даламбера
Шуклина А.Ф.
Микротема 3-1
18.
Знакопостоянные рядыПризнаки сходимости
∞
X
1
n
n
n=1
√
n
lim
n→∞
r
un = lim
= lim
n→∞
n→∞
n
1
=
nn
1
=0=q<1
nn
Вывод: сходится по признаку Коши
Шуклина А.Ф.
Микротема 3-1
19.
Знакопостоянные рядыПризнаки сходимости
При рассмотрении данной микротемы мы изучили:
понятие числового ряда;
понятие частичной суммы ряда;
необходимый признак сходимости числовых рядов;
признаки Даламбера, Коши и сравнения.
Шуклина А.Ф.
Микротема 3-1
20.
Знакопостоянные рядыПризнаки сходимости
Список рекомендуемой литературы
Ильин В.А., Позняк Э.Г. Основы математического анализа. Т1, Т2. М.:
Физматлит, 2005
Кудрявцев Л.Д. Математический анализ. Т1, Т2. М.: Высшая школа, 2003.
Кузнецов Л.А. Сборник заданий по высшей математике. М.: Высшая школа,
2005.
На самостоятельное изучение: Л.В. Апарина Числовые и функциональные
ряды. - Спб.: 2012 г. Параграфы 2-6.
Шуклина А.Ф.
Микротема 3-1
21.
Знакопостоянные рядыПризнаки сходимости
Спасибо за внимание!
Шуклина А.Ф.
Микротема 3-1
















 mathematics
mathematics








