Similar presentations:
Числовые ряды
1. Тема: Ряды
§1. Числовые ряды2. 1.1. Понятие числового ряда
Пусть a1 , a2 , ..., an , ... – числоваяпоследовательность.
Выражение вида
a1 a2 a3
an
an
n 1
называется числовым рядом,
числа a1 , a2 , ..., an , ... – члены
ряда,
a n – n-й или общий член ряда.
(1)
3.
Ряд (1) считается заданным, еслиизвестен общий член ряда, выраженный
как функция его номера n:
an f ( n).
Сумма конечного числа
членов ряда (1)
Sn a1 a2
n первых
an
называется n-й частичной суммой. Таким
образом, S1 a1 , S2 a1 a2 ,...,
Sn a1 a2
an .
4.
Если для последовательности частичныхсумм ряда (1) существует конечный предел
lim Sn S ,
n
то ряд (1) называется сходящимся,
а число –
S – суммой данного ряда (S an ).
n 1
lim S n не существует или равен
Если
n
бесконечности, то ряд (1) называется
расходящимся. Такой ряд суммы не имеет.
5. Пример
1. Ряд 0+0+0+...+0+... сходится, его суммаS=0.
2. Ряд 1+1+1+...+1+... расходится, так как
предел
lim S lim n .
n
n
n
3. Ряд 1-1+1-1+... расходится, так как
последовательность частичных сумм
S1 1, S 2 0, S3 1,... предела не
имеет.
6. Свойства рядов
• 1. Если к ряду (1) прибавить или отброситьконечное число его членов, то полученный
ряд и ряд (1) сходятся или расходятся
одновременно.
• 2. Если ряд (1) сходится и его сумма равна S,
а λ – некоторое число, то ряд
a
n 1
n
a1 a2
an
сходится и его сумма равна λS.
7.
• 3. Если рядыa
n 1
и
n
b
n 1
n
сходятся и их суммы соответственно равны
S1 и S 2
n
то сходится ряд
(an bn )
i 1
и его сумма равна
n
(a
i 1
n
bn ) S1 S2 .
8. Замечания
1. Из свойства 3 вытекает, что сумма(разность) сходящегося и расходящегося
рядов есть расходящийся ряд.
2. Сумма (разность) двух расходящихся
рядов может быть как сходящимся, так и
расходящимся рядом.
9.
Рядan 1 an 2
a
k n 1
k
называется n-м остатком ряда (1). Он
получается из ряда (1) отбрасыванием n
первых его членов.
Ряд
(1)
получается
из
остатка
добавлением конечного числа членов.
Поэтому согласно свойству 1, ряд (1) и его
остаток одновременно сходятся или
расходятся.
10.
Из свойства 1 также следует , что еслиряд (1) сходится, то его остаток
rn S Sn an 1 an 2
стремится к нулю при n :
lim rn 0.
n
11. Необходимый признак сходимости ряда
Если рядa
n 1
n
сходится, то общий член ряда a n стремится
к нулю при n , т.е.
lim an 0.
n
12. Достаточный признак расходимости ряда
Еслиlim an 0
n
или не существует, то ряд
расходится.
a
n
n 1
13. Пример
Исследовать сходимость рядаn 1
1.
;
n 1 2 n 1
2
n
2. 3
.
n 1 n 2
Решение. 1. Найдем предел общего члена
ряда:
1
1
n 1
1
n
lim
lim
0
n 2n 1
n
2
2 1
n
14.
2.2
1
n
n
lim 3
lim
0.
n n 2
n
1 2 3
n
15. §2. Достаточные признаки сходимости рядов с положительными членами
16.
Первый признак сравненияЕсли для членов рядов
a
n 1
n
(2)
b (3)
n 1
n
справедливо неравенство 0 an bn
для всех n n0 N , то
• из сходимости ряда (3) следует сходимость
ряда (2);
• из расходимости ряда
(2) следует
расходимость ряда (3).
17. Второй признак сравнения
Пустьa
n 1
и
n
b
n 1
n
– ряды с положительными членами, причем
существует конечный и отличный от нуля
предел
an
lim A 0.
n b
n
Тогда ряды
bn
an ,
n 1
n 1
сходятся или расходятся одновременно.
18. Ряды, используемые при применении признаков сравнения
1.Гармонический ряд –
1 1
1
1
2 3
n 1 n
расходящийся ряд.
1
n
19.
2. Ряд, составленный из членов геометрической прогрессии,a aq aq
2
aq
n 1
,
a 0,
• при
q 1
сходится и его сумма равна
a
S
,
1 q
• при
q 1
расходится.
20.
Обобщенный гармонический ряд1
1
1
1 p p
p
2
3
n 1 n
p 0,
при
при
p 1 сходится,
0 p 1
расходится.
1
p
n
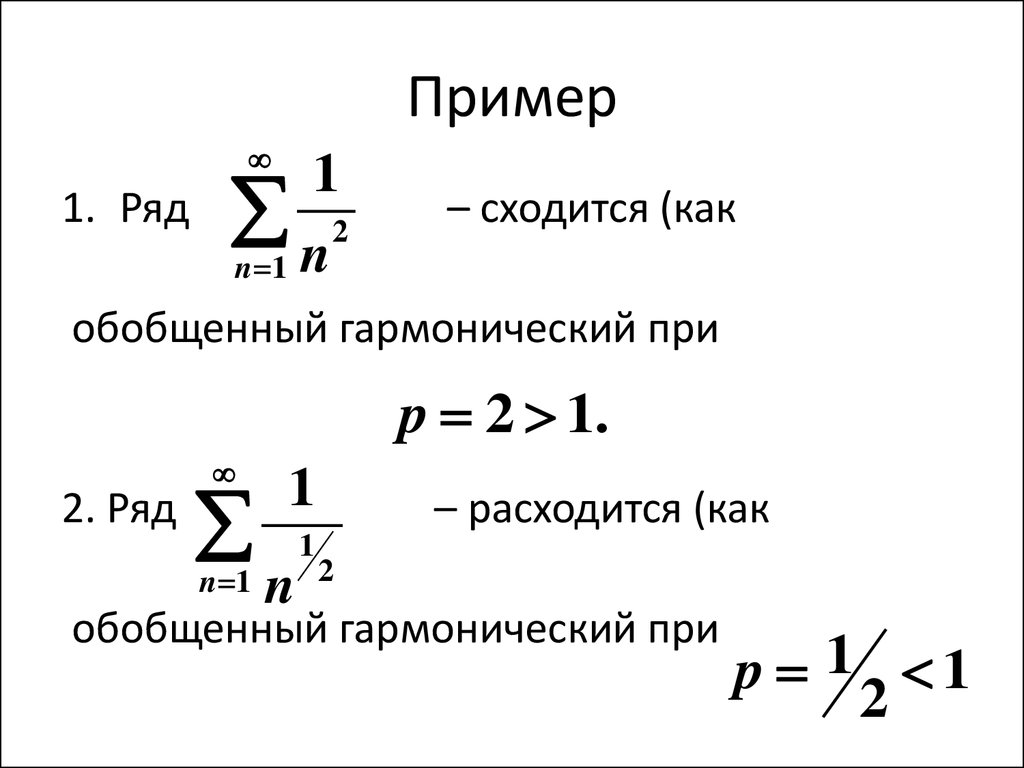
21. Пример
11. Ряд 2
n 1 n
– сходится (как
обобщенный гармонический при
p 2 1.
2. Ряд
n 1
1
1
n
– расходится (как
2
обобщенный гармонический при
p 1 1
2
22. Признак Даламбера
Пустьa
n 1
– ряд с положительными
n
членами, и существует конечный предел
an 1
lim
l.
n a
n
Тогда, если
если же
l 1 , то данный ряд сходится;
l 1
, то – расходится.
23.
Еслиl 1
то ряд может сходиться или расходиться.
Ряд требуется исследовать с помощью других
признаков сходимости.
24. Вспомогательные сведения
0! 11! 1
n! 1 2 3 n
(n 1)! 1 2 3 n (n 1) n! (n 1)
25. Пример
1. Записать общий член ряда, 2 первых членаряда и (n+1 )-й член ряда.
n
4
3
n 1 n
Решение. Формула общего члена ряда:
n
4
an 3
n
26.
Подставляя в формулу общего члена рядавместо n значения 1, 2, n+1, получим
1
4
a1 3 4
1
2
4
a2 3 2
2
n 1
4
an 1
3
( n 1)
27.
2. Используя признак Даламбера исследоватьряд на сходимость. n
2
n 1 n !
n
Решение.
2
общий член ряда: an
n!
(n+1)-й член ряда:
n 1
2
an 1
(n 1)!
28.
Найдемn 1
an 1
2 n!
2 2 n!
lim
lim
lim
n
n
n a
n ( n 1)! 2
n n !( n 1) 2
n
n
2
lim
0 1
n n 1
По признаку Даламбера ряд сходится.
29. §3. ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ
30. 3.1. Знакочередующиеся ряды
Ряд видаa1 a2 a3 a4
( 1)
n 1
n 1
an
( 1)
n 1
an
(4)
где an 0
для всех n N , называется
знакочередующимся.
31. Признак Лейбница
Пусть дан знакочередующийся ряд (4). Есливыполнены два условия
1) последовательность абсолютных величин
членов ряда монотонно убывает:
a1 a2 a3
an
;
2) общий член ряда стремится к нулю при
n : lim an 0,
n
то ряд сходится. При этом сумма ряда
удовлетворяет неравенствам 0 S a1 . (5)
32. Замечания
1. Ряды вида (4), для которых выполняютсяусловия теоремы Лейбница, называются
лейбницевскими (или рядами Лейбница).
2. Соотношение (5) позволяет получить
простую и удобную оценку ошибки,
которую мы допускаем, заменяя сумму S
данного ряда его частичной суммой S n .
33.
Отброшенный ряд (остаток) представляетсобой также знакочередующийся ряд
( 1)
n 1
( a n 1 an 2
)
сумма которого по модулю меньше первого
члена этого ряда, т. е.
S n an 1 .
Поэтому ошибка меньше модуля первого из
отброшенных членов.
34. Абсолютная сходимость
Знакочередующийся ряд называется
абсолютно
сходящимся,
если
ряд,
составленный из модулей его членов,
сходится. В этом случае сходится и сам
знакочередующийся ряд.
• Знакочередующийся
ряд
называется
условно сходящимся, если ряд из модулей
его
членов
расходится,
а
сам
знакочередующийся ряд сходится.
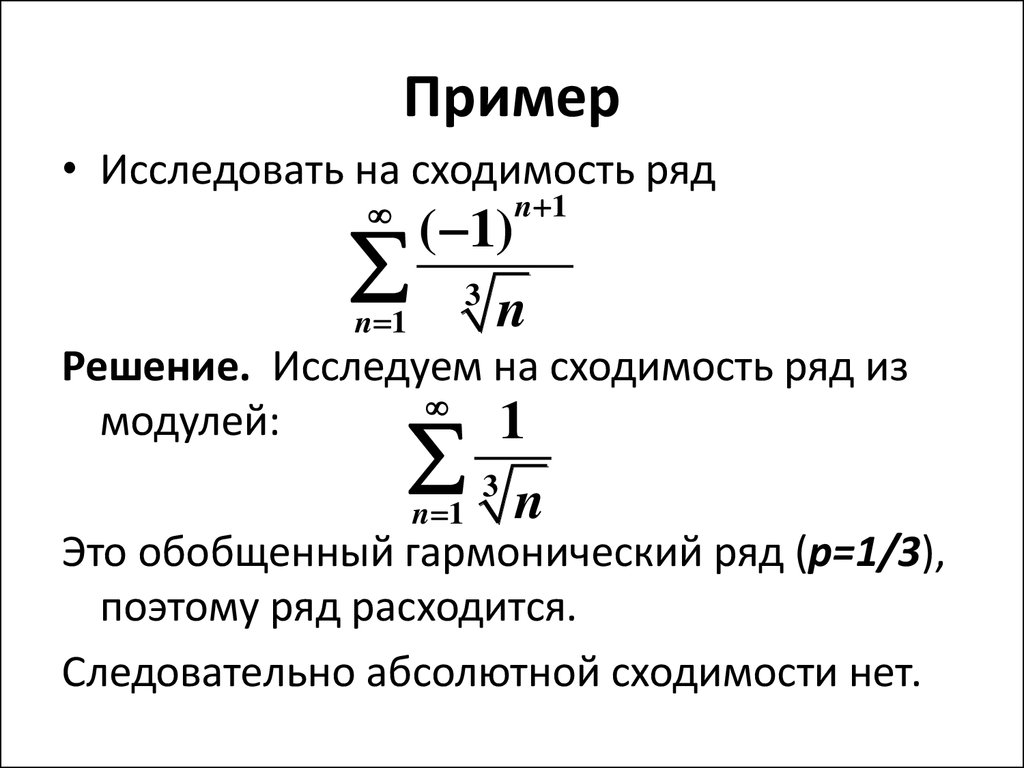
35. Пример
• Исследовать на сходимость рядn 1
( 1)
3
n
n 1
Решение. Исследуем на сходимость ряд из
модулей:
1
n 1
3
n
Это обобщенный гармонический ряд (p=1/3),
поэтому ряд расходится.
Следовательно абсолютной сходимости нет.
36.
Выясним, сходится ли он условно.Используем признак Лейбница:
1) последовательность абсолютных величин
членов ряда монотонно убывает:
1
1
1 3 3
2
3
1
3
n
;
2) общий член ряда стремится к нулю:
1
lim 3 0,
n
n
37.
Таким образом, рядn 1
сходится условно.
1
3
n













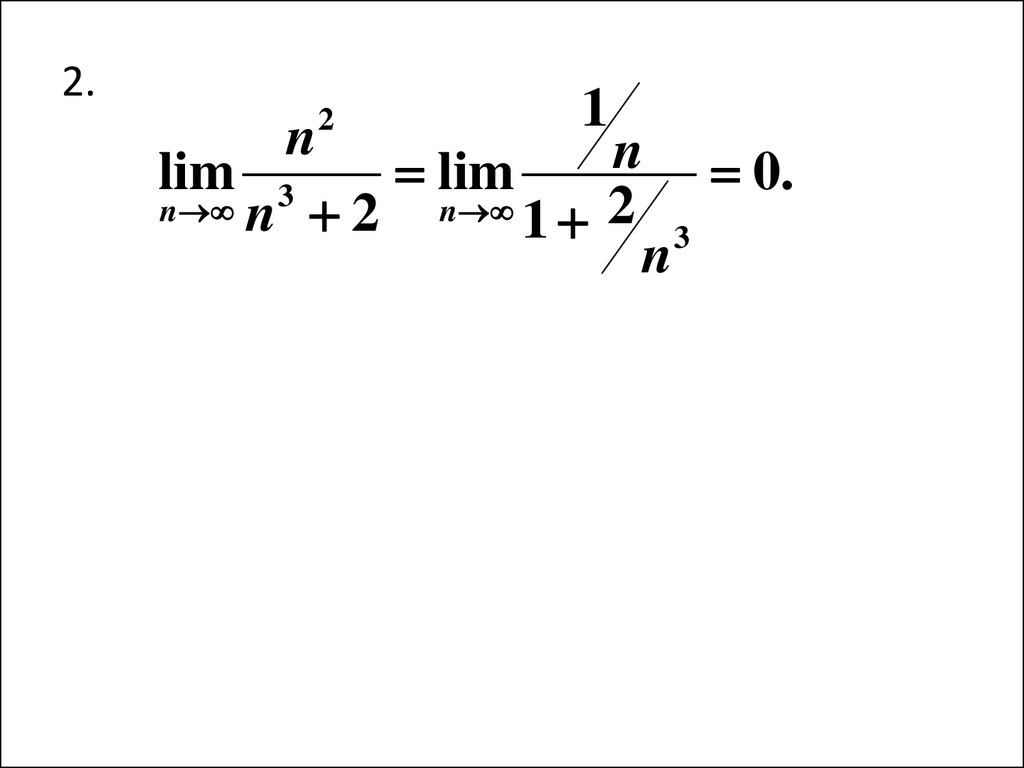





















 mathematics
mathematics








