Similar presentations:
Мультиколлинеарность. Понятие, признаки, методы устранения
1.
Мультиколлинеарность: понятие,признаки, методы устранения
2. Мультиколлинеарность
Слайд №1Мультиколлинеарность
Мультиколлинеарность – совместная, или множественная,
взаимозависимость объясняющих переменных. Выделяют:
1.
Полную мультиколлинеарность - если существует
функциональная
линейная
зависимость
между
объясняющими переменными, определяется нарушением
одного из требований КЛММР, а именно, требования к
рангу матрицы Х .
2.
Реальная (или частичная) мультиколлинеарность
возникает в случаях существования достаточно тесных
линейных статистических связей между объясняющими
переменными.
3. Полная мультиколлинеарность и ее последствия
XTXСлайд №2
Полная мультиколлинеарность и ее
последствия
Когда между объясняющими переменными существует функциональная
зависимость
(полная
мультиколлинеарность),
то
матрица
объясняющих переменных (матрица Х) вырождена, так как ранг
матрицы Х меньше к+1, что в свою очередь, приводит к вырожденности
,а это значит не существует обратная к этой матрице, и следовательно
невозможно оценить коэффициенты методом наименьших квадратов.
Полную мультиколлинеарность несложно избежать уже на предварительной
стадии анализа и отбора множества объясняющих переменных, например в
матрице X T X , определяя ее ранг (например, методом элементарных
преобразований) выявить, какие строки линейно зависят от других строк.
Выявив эти строки, из модели линейной регрессии исключаются
соответствующие этим строкам объясняющие переменные. Таким образом,
строится регрессионную модель меньшей размерности, а по оставшимся
объясняющим переменным матрица X T X будет невырожденна.
4. Реальная (частичная) мультиколлинеарность
Слайд №3Реальная (частичная) мультиколлинеарность
При сильной статистической связи объясняющих
переменных (реальной мультиколлинеарности) матрица
X X
становится плохо (слабой) обусловленной – ее
определитель близок к нулю. При этом элементы матрицы
(X X )
вычисляются
с
большой
погрешностью,
следовательно, и оценки, полученные МНК, тоже
определены с погрешностью. Это, как правило, влечет за
собой и увеличение дисперсии оценок коэффициентов в
регрессионной модели, следовательно, и процедуры
проверки существенности параметров, которые будут
давать смещенные результаты. Такое смещение означает,
что в ряде случаев наш вывод, согласно которому
некоторые оценки незначительно отличаются от нуля, будет
ложным.
T
T
1
5. Внешние признаки реальной мультиколлинеарности
Слайд №4неоправданно большие с экономической точки зрения
значения оценок коэффициентов уравнения регрессии;
небольшие изменения исходных статистических данных
приводит
к
существенному
изменению
оценок
коэффициентов модели, вплоть до изменения их знаков;
неправильные с экономической точки зрения знаки
отдельных коэффициентов регрессии;
среди коэффициентов уравнения регрессии много (может
быть все) незначимы, а модель значима;
стандартные отклонения велики на столько, что сравнимы
или даже превосходят сами коэффициенты;
доверительные интервалы для коэффициентов уравнения
регрессии содержат внутри себя точку ноль.
6. Формальные признаки мультиколлинеарности
Слайд №5Формальные признаки мультиколлинеарности
среди значимых коэффициентов парной или частной
корреляции объясняющих переменных есть такие, которые по
абсолютной величине достаточно велики (превышают 0,750,8);
достаточно высокие значение множественного коэффициента
корреляции (детерминации) одной из объясняющих
переменных на другие ;
необходимым условием плохой обусловленности является
малость определителя матрицы
. Если значение
оказывается близким к нулю, то свидетельствует о наличии
мультиколлинеарности.
достаточным
условием
плохой
обусловленности
(мультиколлинеарности) является большое значение числа
обусловленности.
M
max i
min i
i 1, n , где
i - собственное число матрицы X T X
7.
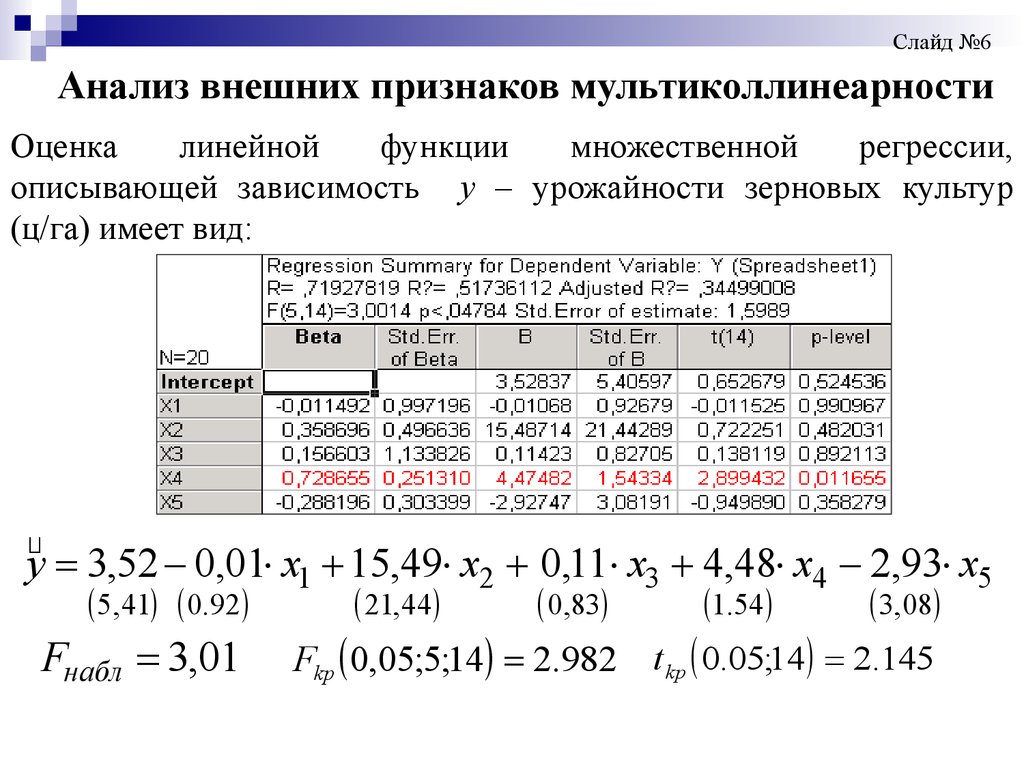
Слайд №6Анализ внешних признаков мультиколлинеарности
Оценка
линейной
функции
множественной
регрессии,
описывающей зависимость y – урожайности зерновых культур
(ц/га) имеет вид:
y 3,52 0,01 x1 15,49 x2 0,11 x3 4,48 x4 2,93 x5
5, 41 0.92
Fнабл 3,01
21, 44
0,83
1.54
3,08
Fkp 0,05;5;14 2.982 t kp 0.05;14 2.145
8.
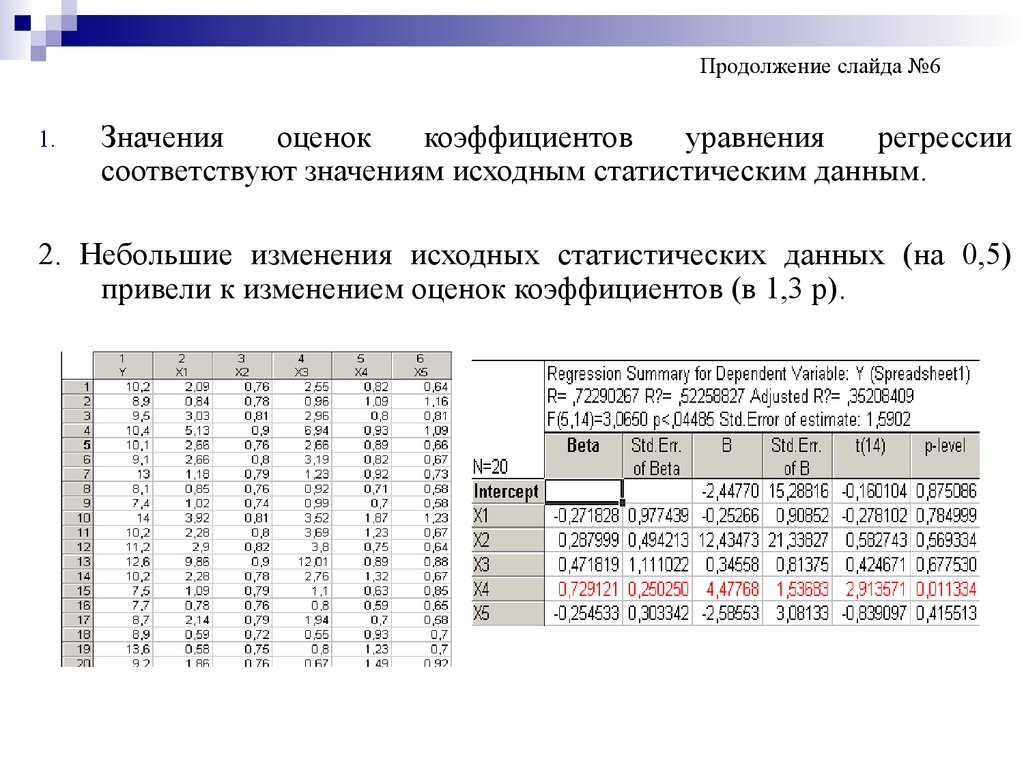
Продолжение слайда №61.
Значения
оценок
коэффициентов
уравнения
регрессии
соответствуют значениям исходным статистическим данным.
2. Небольшие изменения исходных статистических данных (на 0,5)
привели к изменением оценок коэффициентов (в 1,3 р).
9.
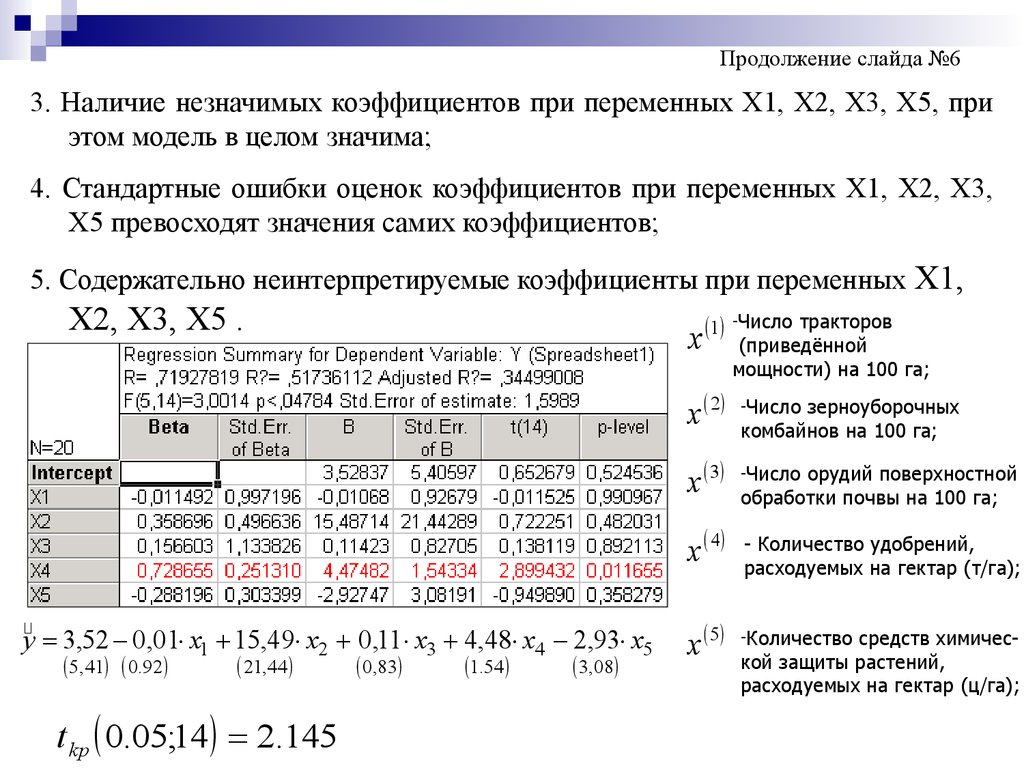
Продолжение слайда №63. Наличие незначимых коэффициентов при переменных Х1, Х2, Х3, Х5, при
этом модель в целом значима;
4. Стандартные ошибки оценок коэффициентов при переменных Х1, Х2, Х3,
Х5 превосходят значения самих коэффициентов;
5. Содержательно неинтерпретируемые коэффициенты при переменных Х1,
Х2, Х3, Х5 .
1 -Число тракторов
x
x 2
-Число
x 3
-Число
x 4
y 3,52 0,01 x1 15,49 x2 0,11 x3 4,48 x4 2,93 x5
5, 41 0.92
21, 44
t kp 0.05;14 2.145
0,83
1.54
3,08
(приведённой
мощности) на 100 га;
x 5
зерноуборочных
комбайнов на 100 га;
орудий поверхностной
обработки почвы на 100 га;
- Количество удобрений,
расходуемых на гектар (т/га);
-Количество
средств химической защиты растений,
расходуемых на гектар (ц/га);
10.
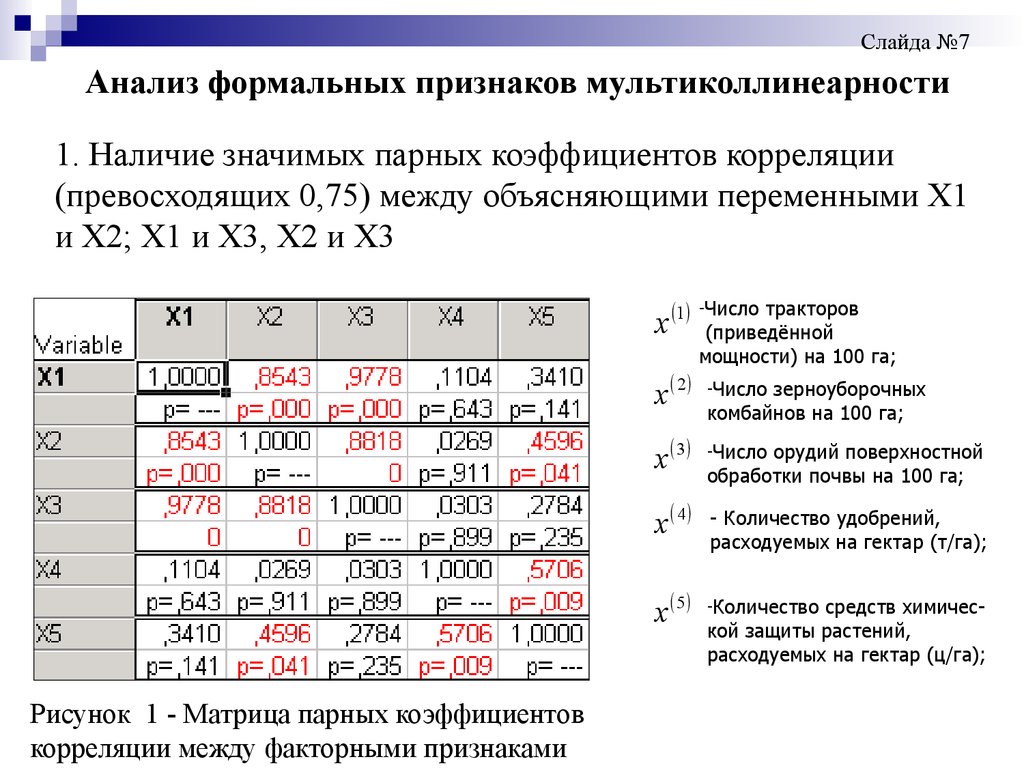
Слайда №7Анализ формальных признаков мультиколлинеарности
1. Наличие значимых парных коэффициентов корреляции
(превосходящих 0,75) между объясняющими переменными Х1
и Х2; Х1 и Х3, Х2 и Х3
x 1
x 2
x 3
x 4
x 5
Рисунок 1 - Матрица парных коэффициентов
корреляции между факторными признаками
-Число
тракторов
(приведённой
мощности) на 100 га;
-Число
зерноуборочных
комбайнов на 100 га;
-Число
орудий поверхностной
обработки почвы на 100 га;
- Количество удобрений,
расходуемых на гектар (т/га);
-Количество
средств химической защиты растений,
расходуемых на гектар (ц/га);
11.
Продолжение слайда №72. Наличие высоких коэффициентов детерминации R x2j / x1 .. x j 1 , x j 1 ,.., xk
R
2
x1 / x2 , x3 , x4 , x5
0,97
Rx22 / x1 , x3 , x4 , x5 0,86
2
Rx3 / x1 , x2 , x4 , x5
2
Rx4 / x1 , x2 , x3 , x5
Rx25 / x1 , x2 , x3 , x4
0,98
0,45
0,62
x
1
-Число
тракторов
(приведённой
мощности) на 100 га;
x 2
-Число
x 3
-Число
x 4
x 5
зерноуборочных
комбайнов на 100 га;
орудий поверхностной
обработки почвы на 100 га;
- Количество удобрений,
расходуемых на гектар (т/га);
-Количество
средств химической защиты растений,
расходуемых на гектар (ц/га);
12.
Продолжение слайда №7T
3. Малость определителя матрицы X X
4. Большое значение числа обусловленности матрицы
max | j |
402,318
4
cond X X
7
,
752
10
min | j | 5,19 10 3
T
XTX
13. Методы устранения мультиколлинеарности
Слайда №8Методы устранения мультиколлинеарности
1. . Метод пошаговой регрессии :
- с включением переменных
- с исключением переменных
2. Метод «ридж-регрессии
3. Метод главных компонент
14. Метод пошаговой регрессии
Слайд №9Метод пошаговой регрессии
Метод пошаговой регрессии с включением переменных
Решается задача: для заданного значения l ( l 1, k 1 ) путем
перебора возможных комбинаций из l объясняющих переменных,
отобранных из исходного набора x1 , x2 ,...xê , определить такие
x i l , x i l ,..., x i l , для которых коэффициент
переменные
0
1
детерминации с
максимальным.
0
2
0
l
результирующим
Rˆ 2
y/
ilo ( l )
i10 ( l )
x
,.., x
показателем
max
1 i1 , i 2 ,..i l k
Rˆ 2
i
y
i
y / x 1 ,.., x l
был
бы
15.
Продолжение слайда №9На первом шаге процедуры ( l 1 ) определяется одна (первая)
i1 1
x
объясняющая переменная
, которую можно назвать наиболее
информативной, при условии, что в регрессионную модель Y по X
включена только одна из набора объясняющих переменных.
На втором шаге реализация критерия максимальности
коэффициента
детерминации
определит
уже
наиболее
i 1 i 2
информативную пару переменных x , x , при этом одна из них
определена на предыдущем (первом) шаге. Эта пара будет иметь
наиболее тесную статистическую связь с результирующим
показателем Y .
На третьем шаге ( l 3 ) будет отобрана наиболее
информативная тройка объясняющих переменных и т.д.
1
2
16.
Продолжение слайда №9На каждом шаге определяются несмещенная
коэффициента детерминации
*2
2
n 1
.
R l 1 1 R l
оценка
n l 1
и оценка нижней доверительной границы
2
Rmin
l R* 2 l 2
2
Rmin
l
2
2l n l 1
1
R
l
2
n 1 n 1
для
R2 l
.
Правило отбора объясняющих переменных: предполагается
выбирать в качестве оптимального числа l0 объясняющих
переменных регрессионной модели значение l , при котором
2
величина Rmin
l достигает своего максимума.
17. Метод пошаговой регрессии с исключением переменных
Продолжение слайда №9Метод пошаговой регрессии с
исключением переменных
На первом шаге строится уравнение регрессии на все
k факторных признаков и, если среди его коэффициентов
есть незначимые, то на втором шаге строятся уравнения
регрессии на k 1 признаков, среди которых выбирается то,
которому
соответствует
наибольший
выборочный
коэффициент детерминации. Если и в этой модели есть
незначимые коэффициенты, то процедура повторяется для
k 2 переменных и т. д.
18.
Продолжение слайда №9Пример реализации метода пошаговой регрессии
Шаг 1. Выбираем первую переменную, включаемую в модель:
R y2 / x1 0.185
R y2 / x5 0.11
R y2 / x3 0.163
R y2 / x 2 0.139
R y2 / x 4 0.333
2
2
max R y / xi R y / x 4 0,333
i 1,5
Поправленный на несмещённость коэффициент детерминации:
*2
R y / x 4 0.296
Нижняя граница доверительного интервала
2
1 0.204
Rmin
19.
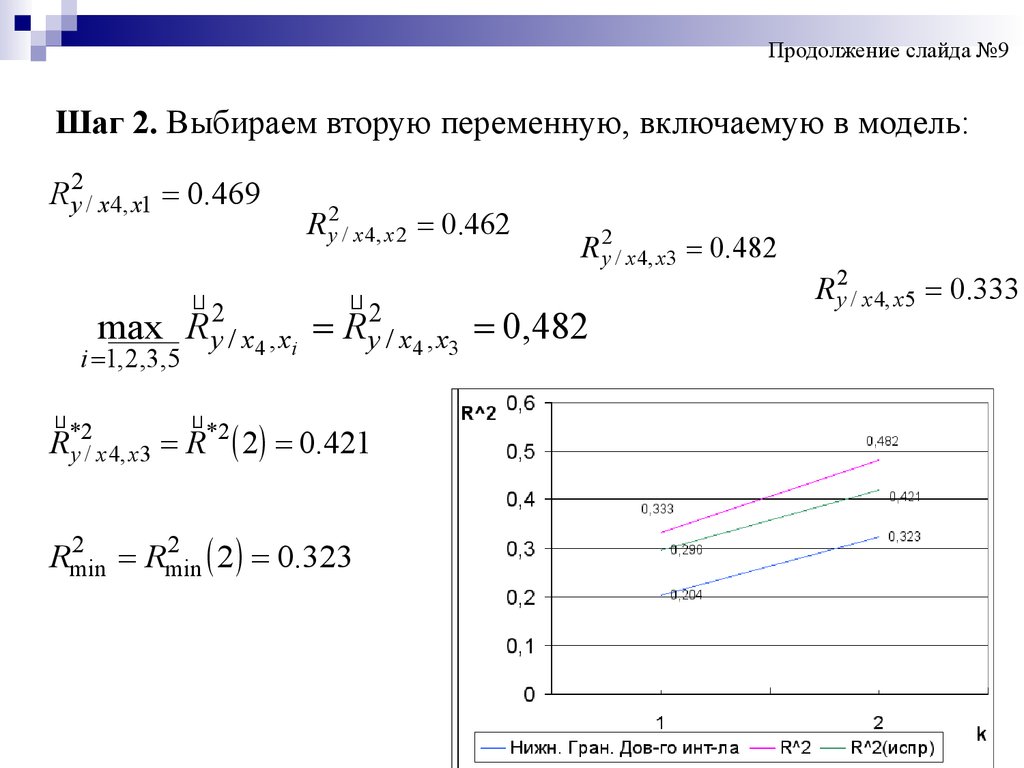
Продолжение слайда №9Шаг 2. Выбираем вторую переменную, включаемую в модель:
R y2 / x 4, x1 0.469
R y2 / x 4, x 2 0.462
R y2 / x 4, x 3 0.482
2
2
max R y / x4 , xi R y / x4 , x3 0,482
i 1, 2,3,5
*2
*2
R y / x 4, x3 R 2 0.421
2
2
2 0.323
Rmin
Rmin
R y2 / x 4, x 5 0.333
20.
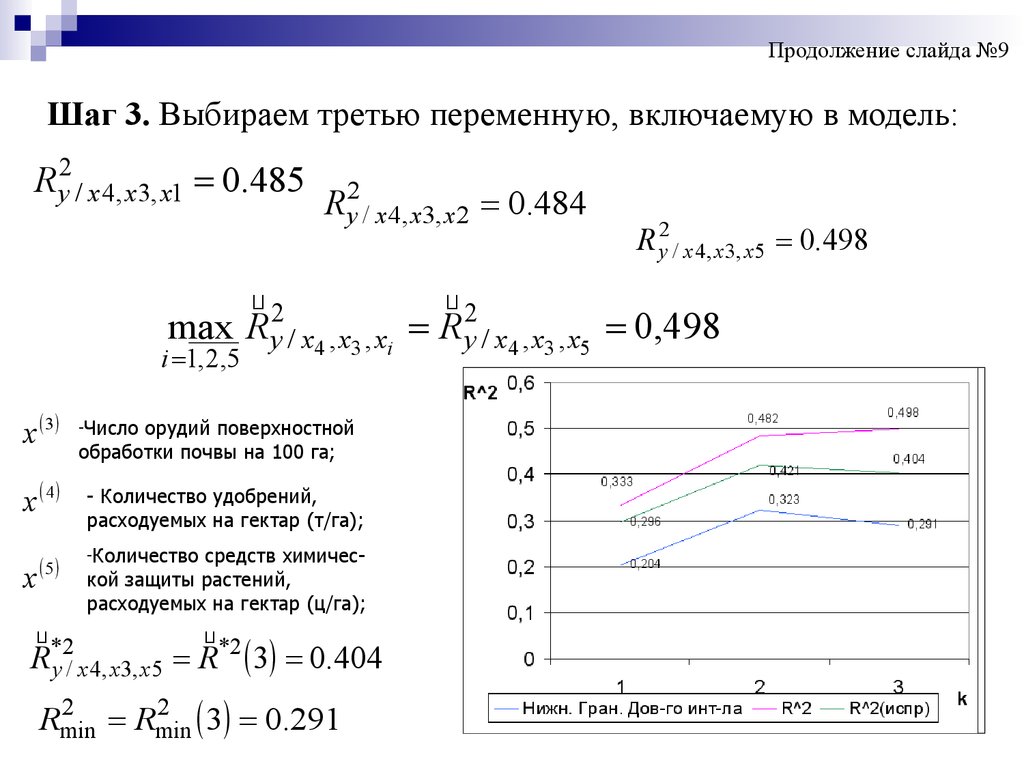
Продолжение слайда №9Шаг 3. Выбираем третью переменную, включаемую в модель:
R y2 / x 4, x3, x1 0.485
R y2 / x 4, x3, x 2 0.484
R y2 / x 4, x3, x 5 0.498
2
2
max R y / x4 , x3 , xi R y / x4 , x3 , x5 0,498
i 1, 2,5
x 3
x 4
x
5
-Число
орудий поверхностной
обработки почвы на 100 га;
- Количество удобрений,
расходуемых на гектар (т/га);
-Количество
средств химической защиты растений,
расходуемых на гектар (ц/га);
*2
*2
R y / x 4, x3, x5 R 3 0.404
2
2
3 0.291
Rmin
Rmin
21.
Продолжение слайда №92
2
3 Rmin
2
Rmin
k0 2 - существенные объясняющие переменные x3, x4:
y 7,29 0,28 x3 3,47 x4
0,66 0,18
x 3
x 4
-Число
орудий поверхностной
обработки почвы на 100 га;
- Количество удобрений,
расходуемых на гектар (т/га);
1,07
Y – Урожайность зерновых
культур (ц/га);
22. Метод ридж-регрессии
Слайд №10Метод ридж-регрессии
Устранение мультиколлинеарности путем построения
смещенных оценок (ридж-регрессия или «гребневая регрессия»).
b ( X T X E p 1 ) 1 X T Y
Добавление к диагональным элементам матрицы ( X T X )
«гребня» ( - некоторое положительное число, 0,1 0,4 , E p 1 единичная матрица ( p 1 ) порядка) с одной стороны, делает
получаемые при этом оценки смещенными, а с другой,- превращает
матрицу
из «плохо обусловленной» в «хорошо
XTX
обусловленную».
















 mathematics
mathematics economics
economics








