Динамика жидких частиц в поле скорости точечного триполя

1. ДИНАМИКА ЖИДКИХ ЧАСТИЦ В ПОЛЕ СКОРОСТИ ТОЧЕЧНОГО ТРИПОЛЯ

Саямов С.М. (3 курс 2 группа)

2. Постановка задачи

wi
dxi
dH
,
dt
dy i
1
H
4
wi
3
w w
i j
1
( x, y )
4
i
j
dy i dH
,
dt
dxi
i 1, 2, 3
ln(( xi x j ) 2 ( y i y j ) 2 )
3
2
2
w
ln((
x
x
)
(
y
y
)
)
i
i
i
i 1
(xi, yi) – координаты i-го вихря, (x, y) - координаты пассивной частицы
wi – завихренность i-го вихря
Ψ – функция тока

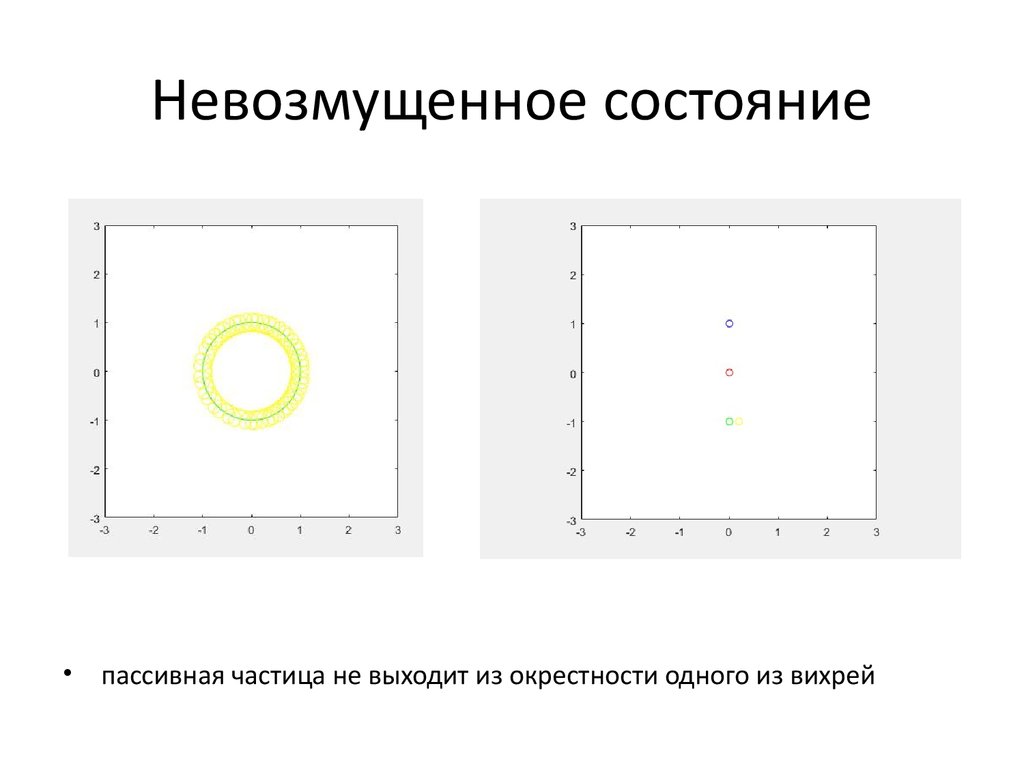
3. Невозмущенное состояние

пассивная частица не выходит из окрестности одного из вихрей

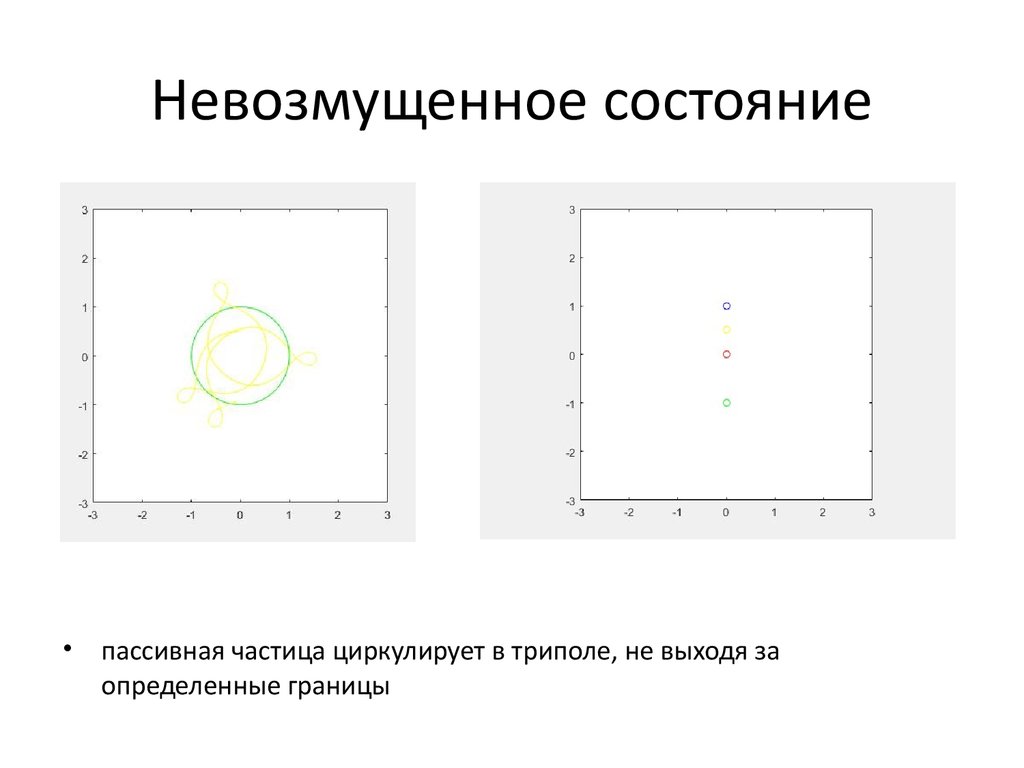
4. Невозмущенное состояние

пассивная частица циркулирует в триполе, не выходя за
определенные границы

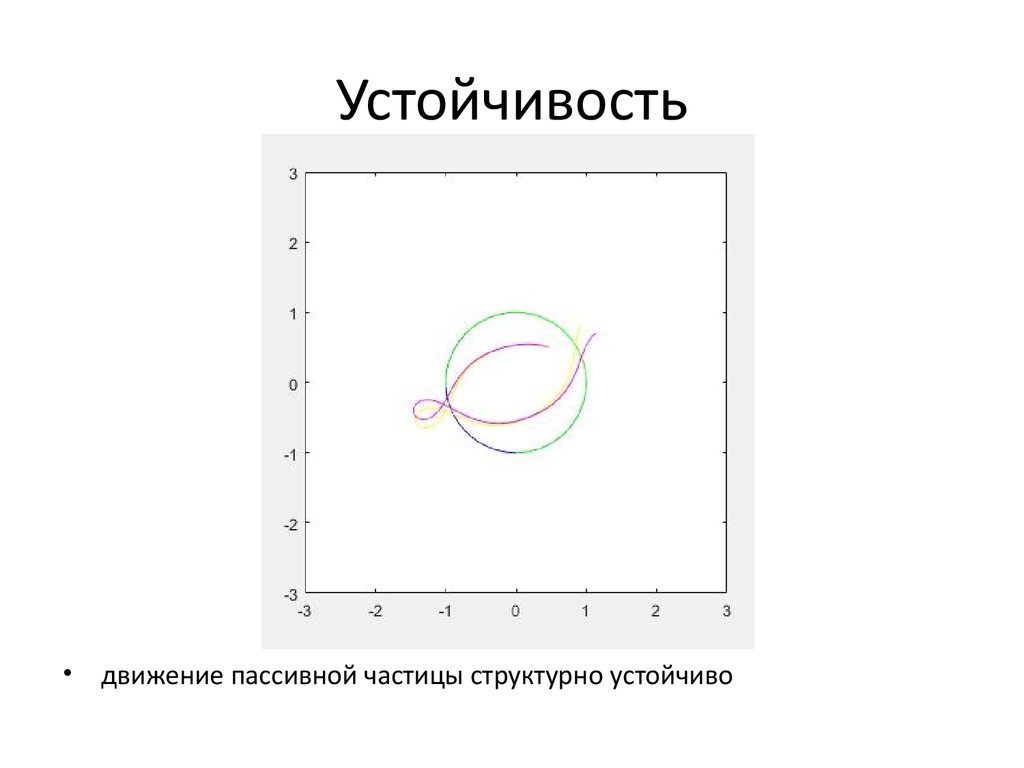
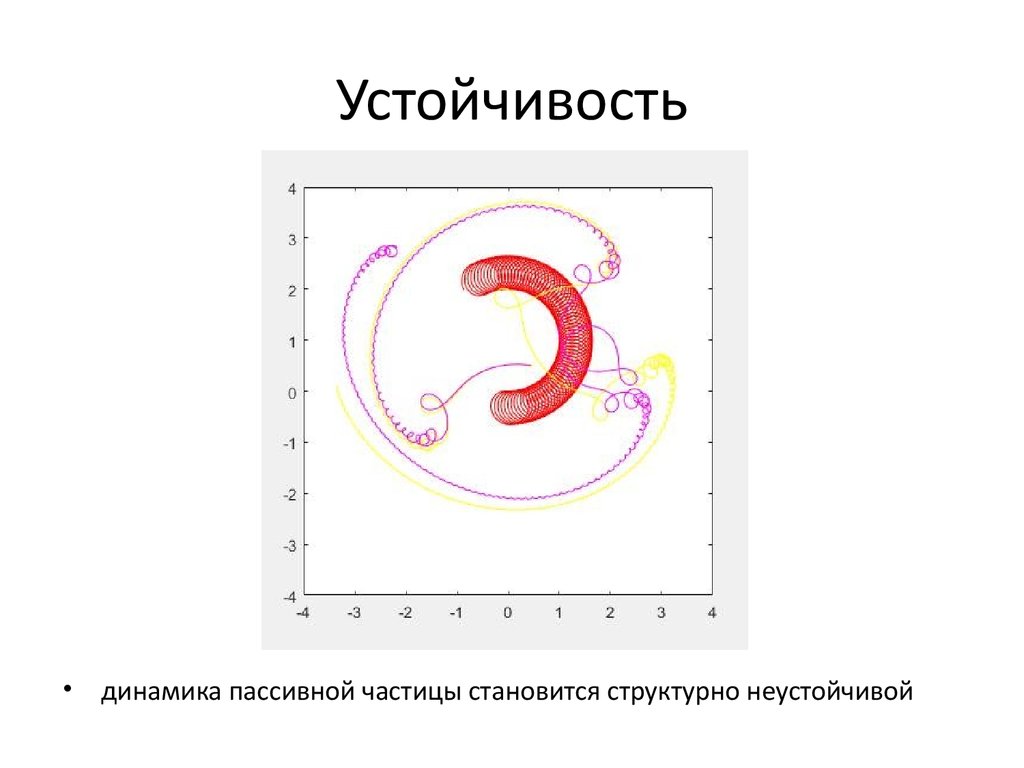
5. Устойчивость

движение пассивной частицы структурно устойчиво

6. Простейшие возмущения

увеличена завихренность одного из спутников

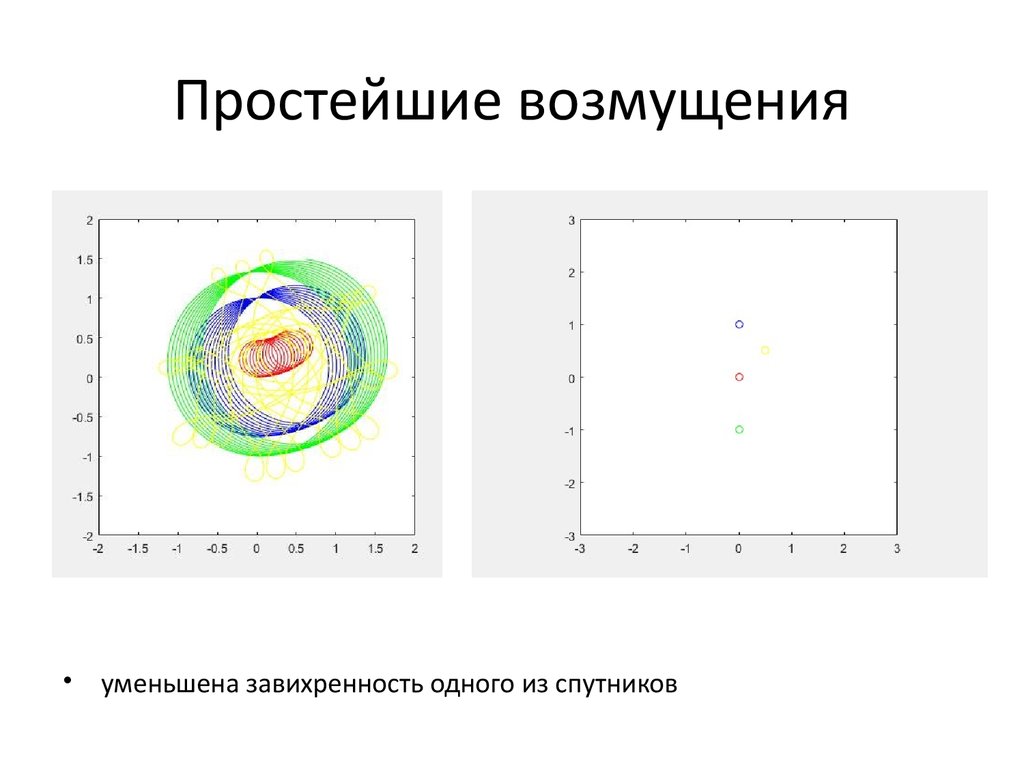
7. Простейшие возмущения

уменьшена завихренность одного из спутников

8. Устойчивость

динамика пассивной частицы становится структурно неустойчивой

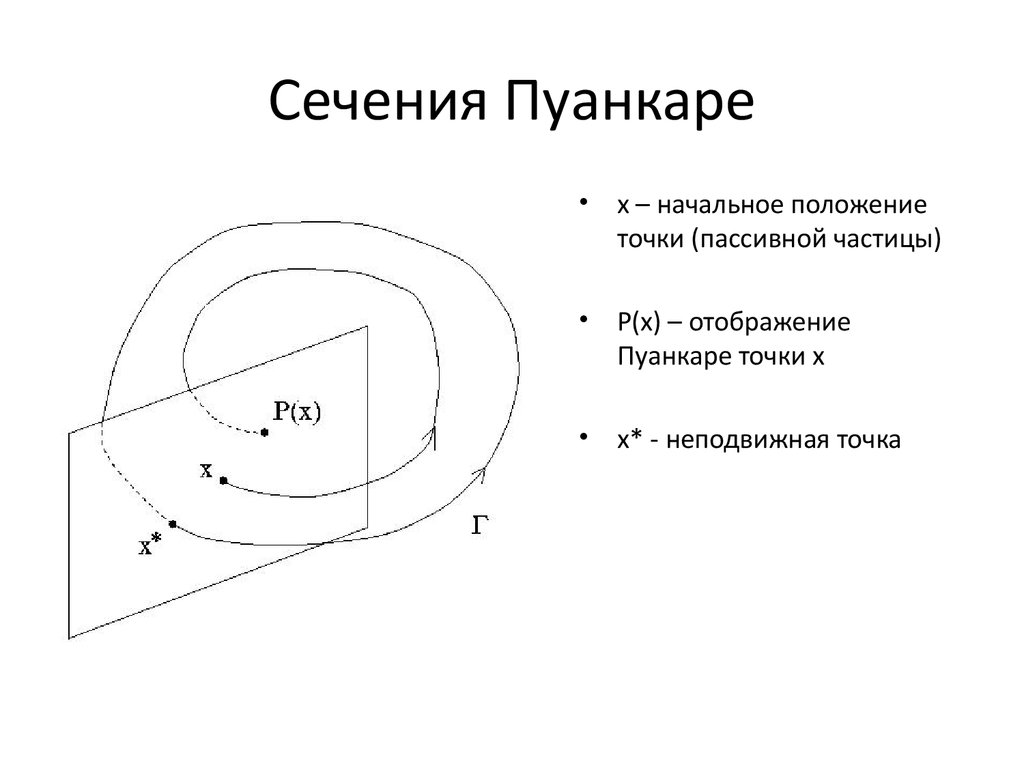
9. Сечения Пуанкаре

x – начальное положение
точки (пассивной частицы)
P(x) – отображение
Пуанкаре точки x
x* - неподвижная точка

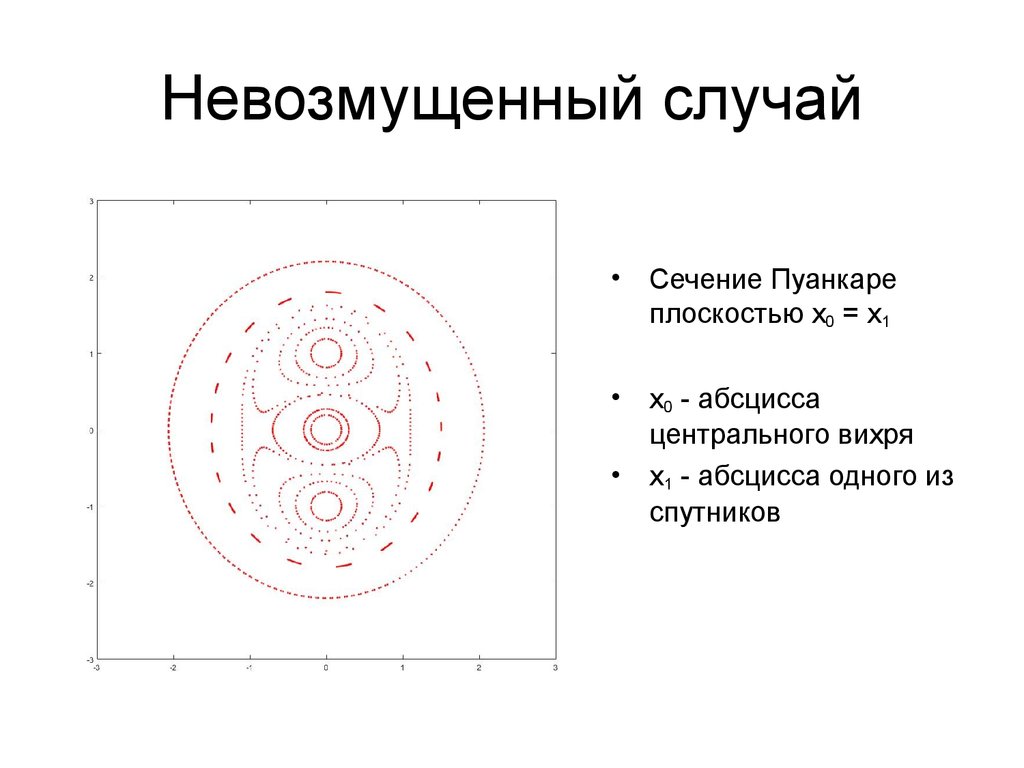
10. Невозмущенный случай

Сечение Пуанкаре
плоскостью x0 = x1
x0 - абсцисса
центрального вихря
x1 - абсцисса одного из
спутников

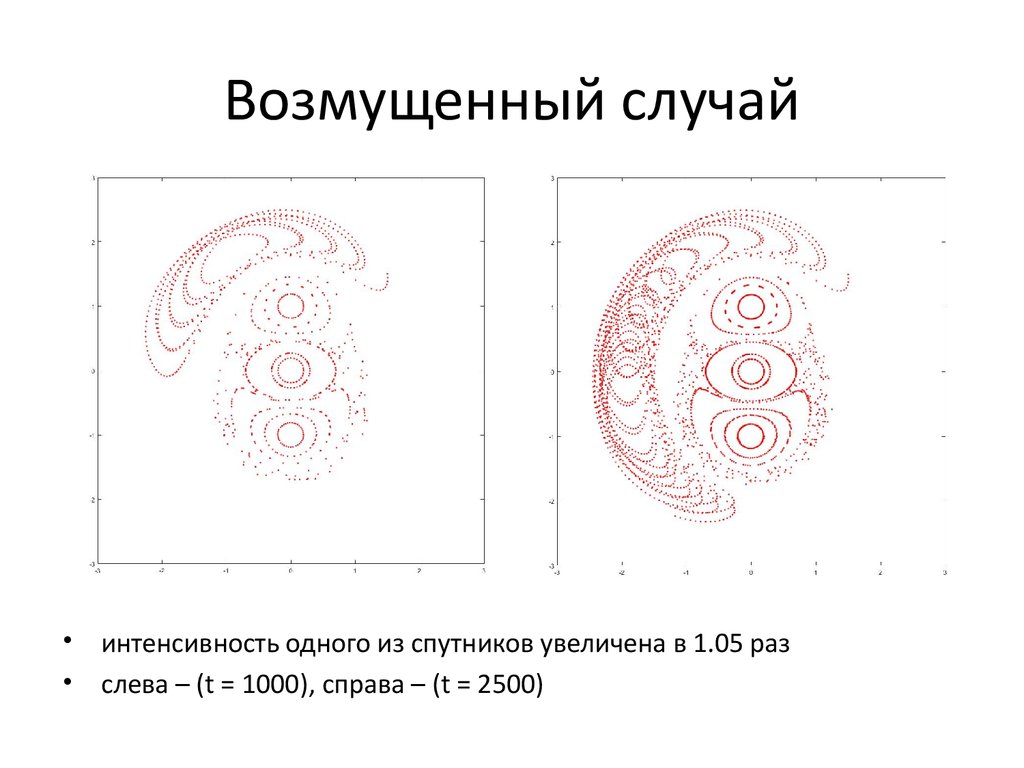
11. Возмущенный случай

интенсивность одного из спутников увеличена в 1.05 раз
слева – (t = 1000), справа – (t = 2500)

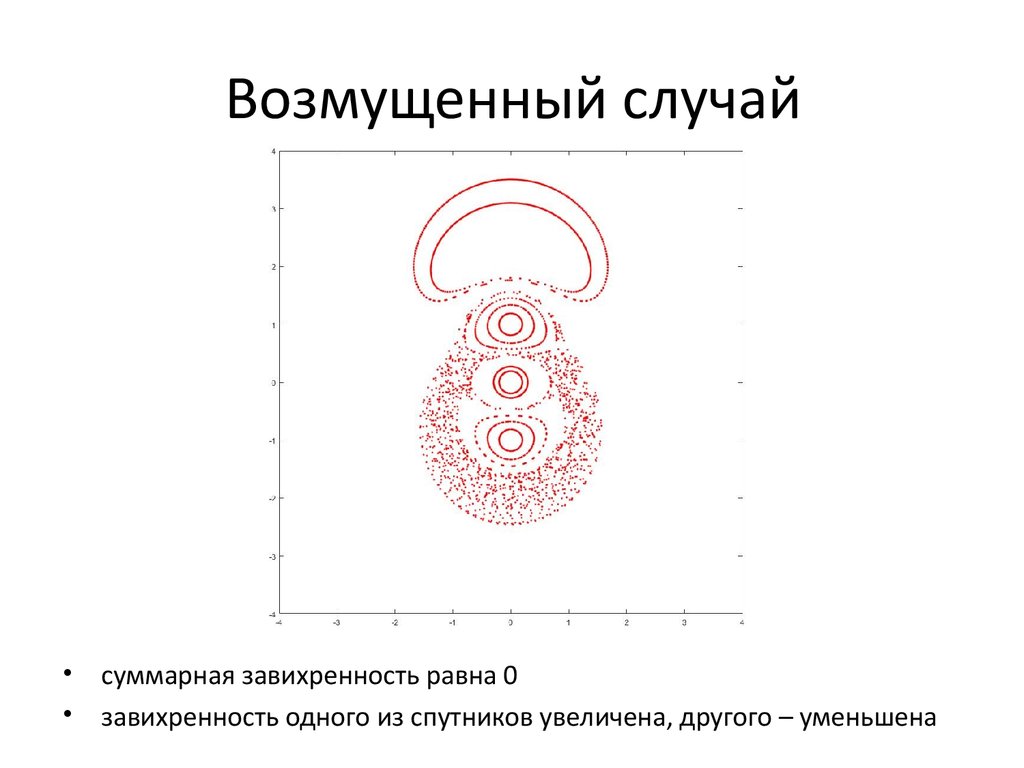
12. Возмущенный случай

суммарная завихренность равна 0
завихренность одного из спутников увеличена, другого – уменьшена