Пересечения прямой и плоскости, когда плоскость проецирующая

1. Раздел № 3 Солодухин Е.А.

1

2.

ОБЯЗАТЕЛЬНО
• Рассмотреть частный случай
ПЕРЕСЕЧЕНИЯ ПРЯМОЙ И
ПЛОСКОСТИ, когда плоскость
проецирующая

3. Плоскость

3

4.

Плоскость это один из видов поверхности
– плоская поверхность.

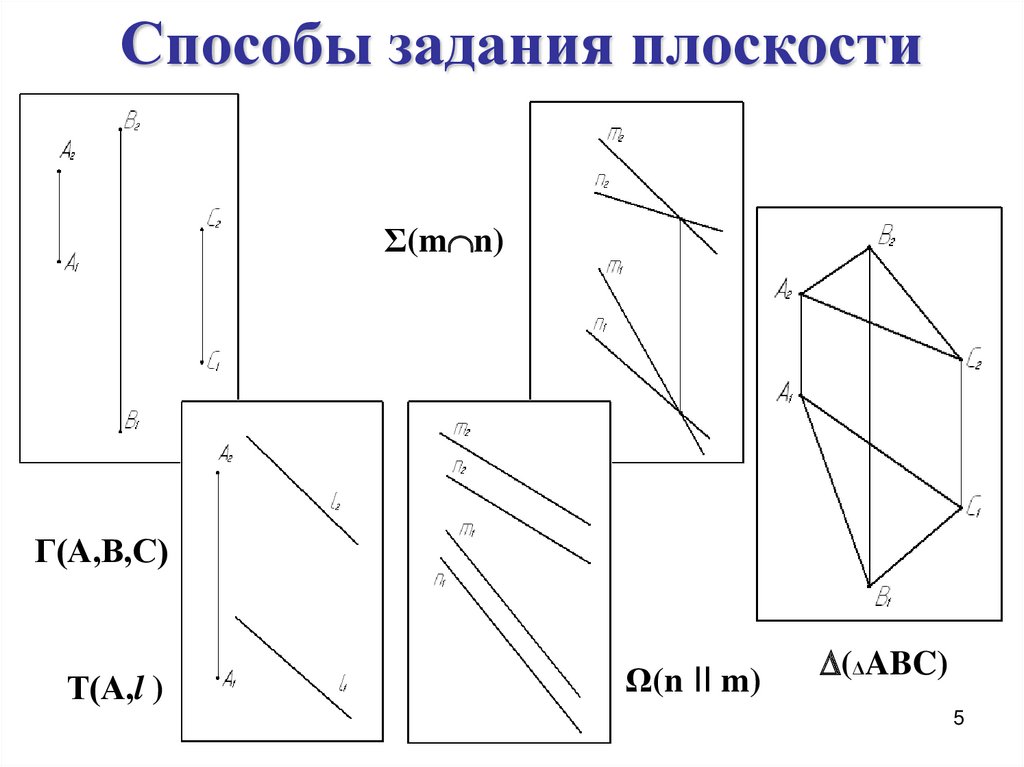
5. Способы задания плоскости

Σ(m n)
Г(А,В,С)
Т(А,l )
Ω(n II m)
(ΔABC)
5

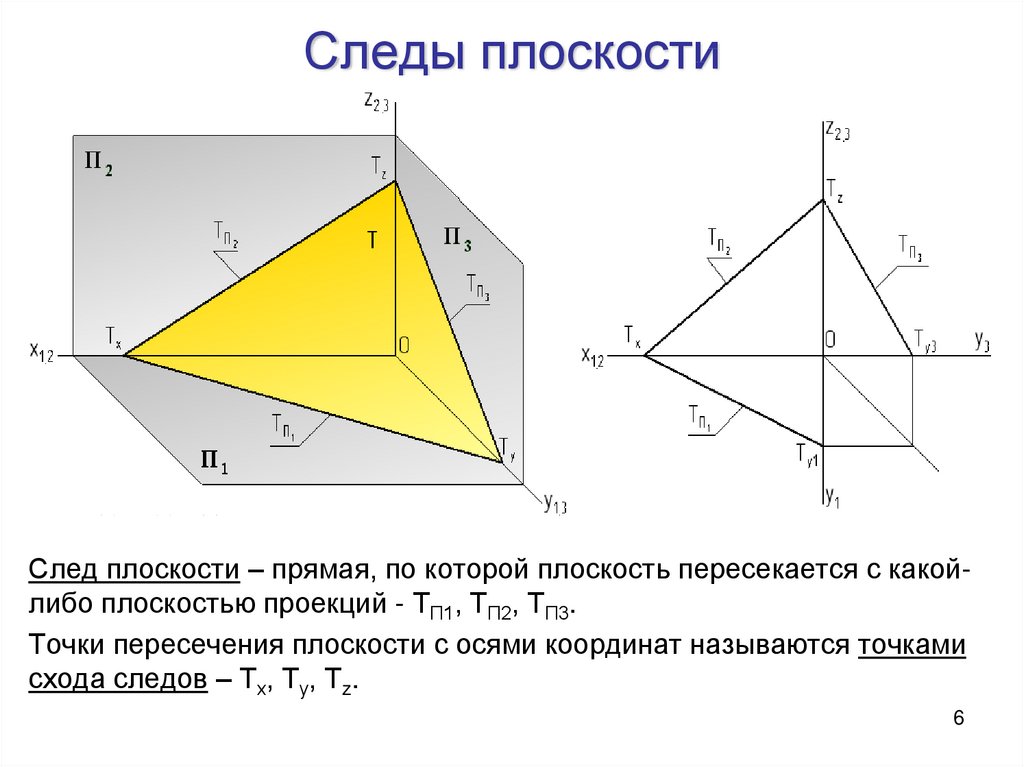
6. Следы плоскости

След плоскости – прямая, по которой плоскость пересекается с какойлибо плоскостью проекций - ТП1, ТП2, ТП3.
Точки пересечения плоскости с осями координат называются точками
схода следов – Тх, Ту, Тz.
6

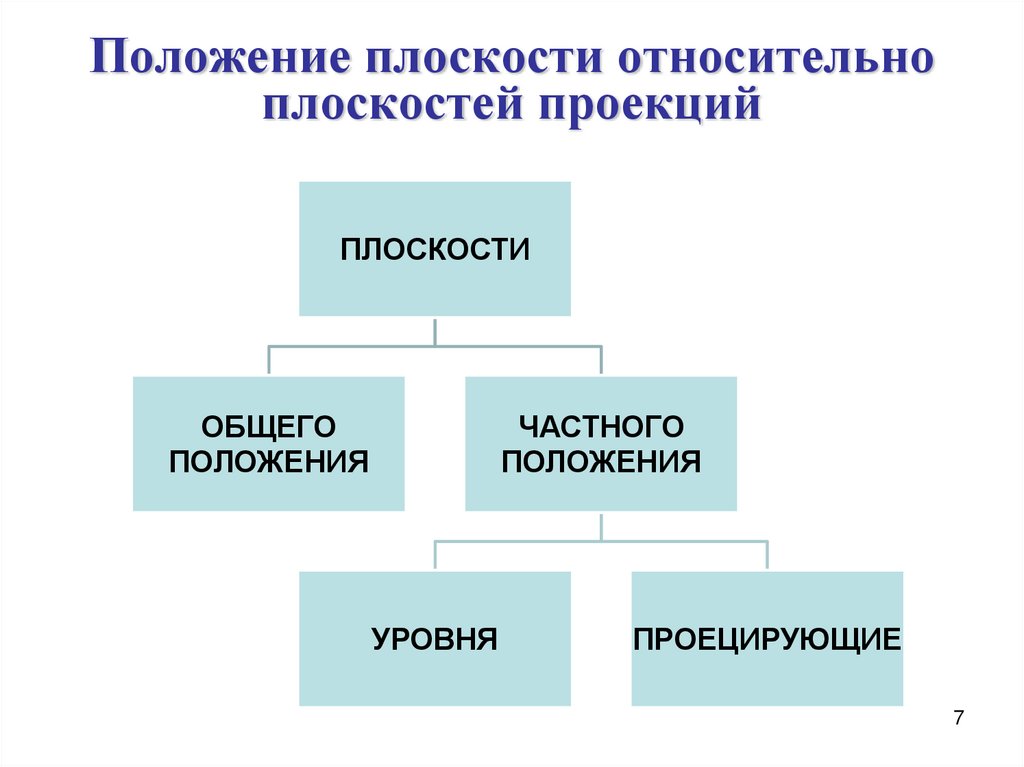
7. Положение плоскости относительно плоскостей проекций

ПЛОСКОСТИ
ОБЩЕГО
ПОЛОЖЕНИЯ
ЧАСТНОГО
ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩИЕ
7

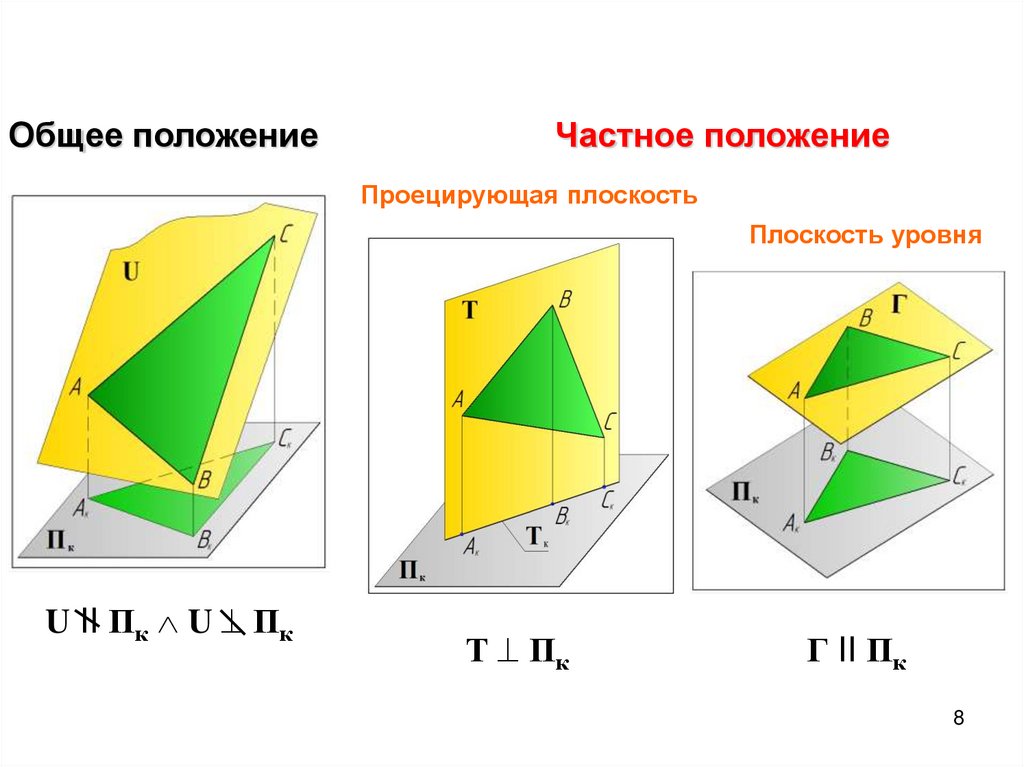
8.

Общее положение
Частное положение
Проецирующая плоскость
Плоскость уровня
U II Пк U Пк
Т Пк
Г II Пк
8

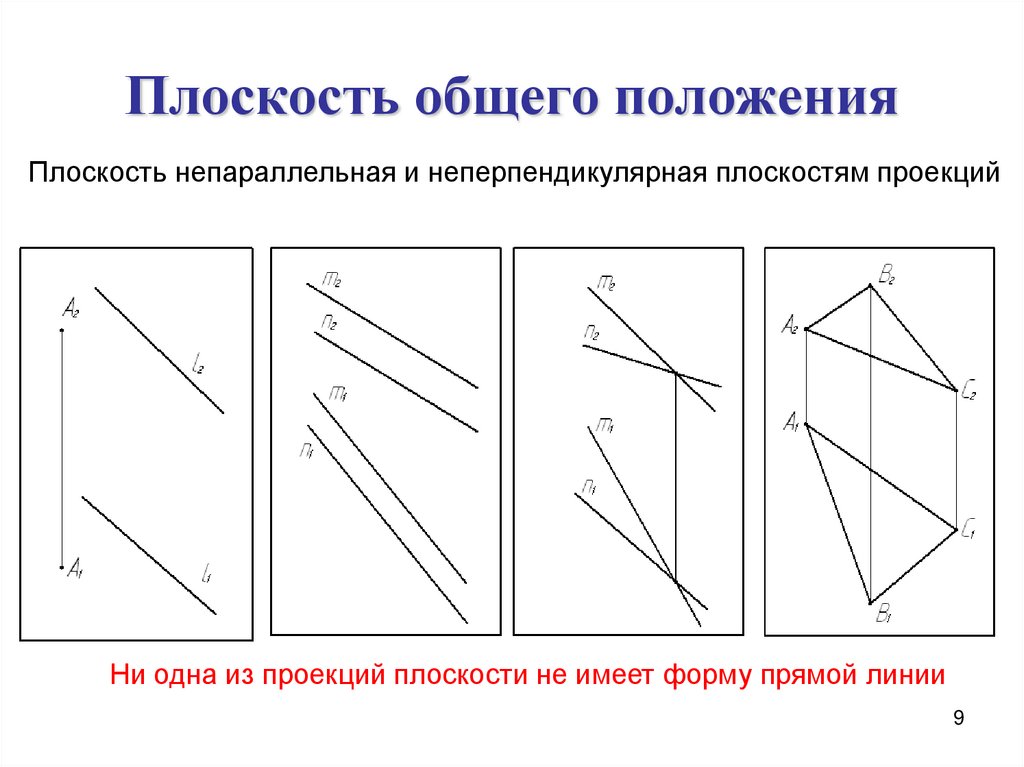
9. Плоскость общего положения

Плоскость непараллельная и неперпендикулярная плоскостям проекций
Ни одна из проекций плоскости не имеет форму прямой линии
9

10. Плоскости частного положения

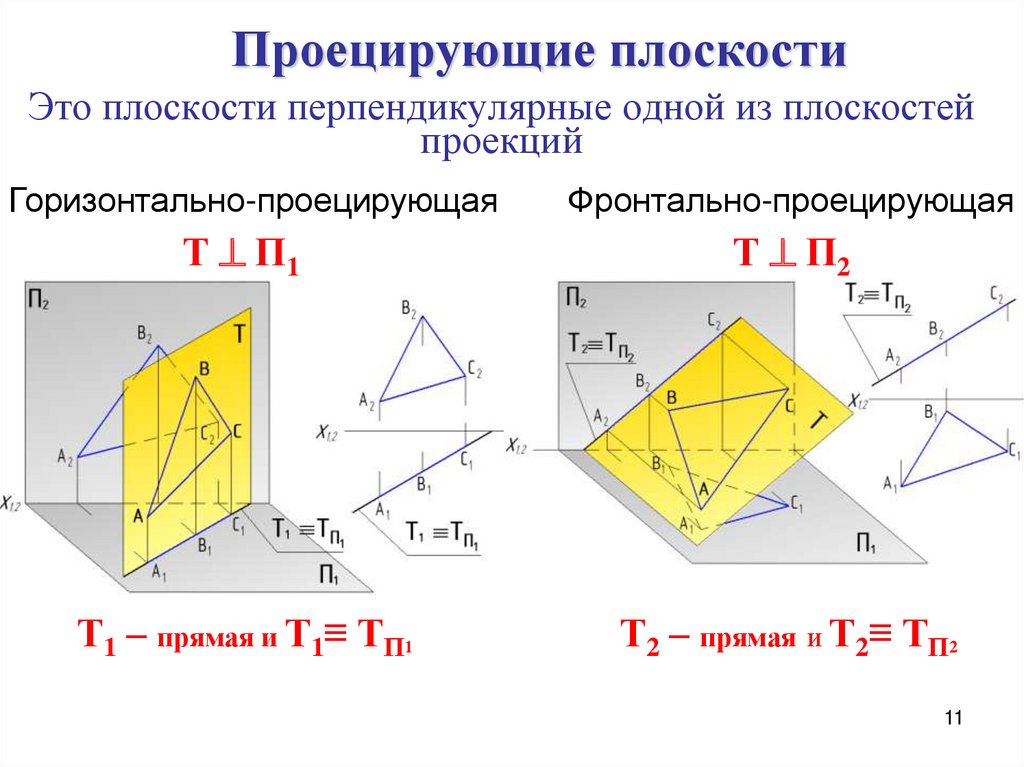
11. Это плоскости перпендикулярные одной из плоскостей проекций

Проецирующие плоскости
Это плоскости перпендикулярные одной из плоскостей
проекций
Горизонтально-проецирующая
Фронтально-проецирующая
Т П1
Т П2
Т1 – прямая и Т1≡ ТП1
Т2 – прямая и Т2≡ ТП2
11

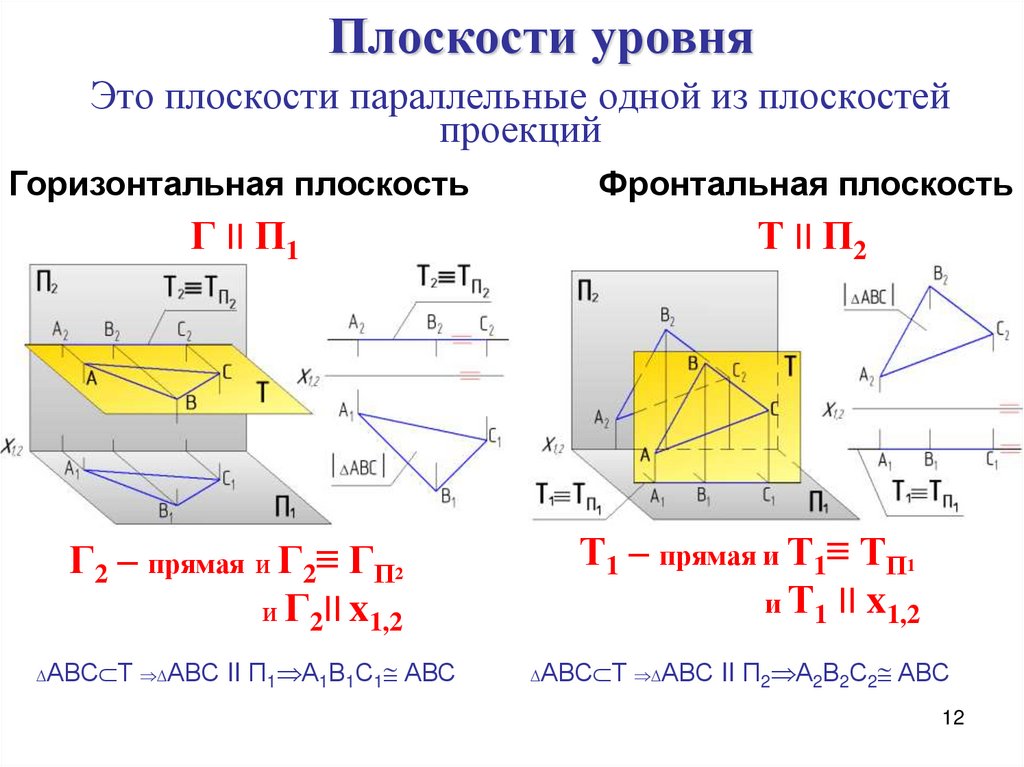
12. Это плоскости параллельные одной из плоскостей проекций

Плоскости уровня
Это плоскости параллельные одной из плоскостей
проекций
Горизонтальная плоскость
Фронтальная плоскость
Г II П1
Т II П2
Г2 – прямая и Г2≡ ГП2
и Г2II x1,2
АВС Т АВС
II П1 А1В1С1 АВС
Т1 – прямая и Т1≡ ТП1
и Т1 II x1,2
АВС Т АВС
II П2 А2В2С2 АВС
12

13.

Вывод:
У плоскости частного положения одна из
проекций обязательно имеет форму прямой
линии.
13

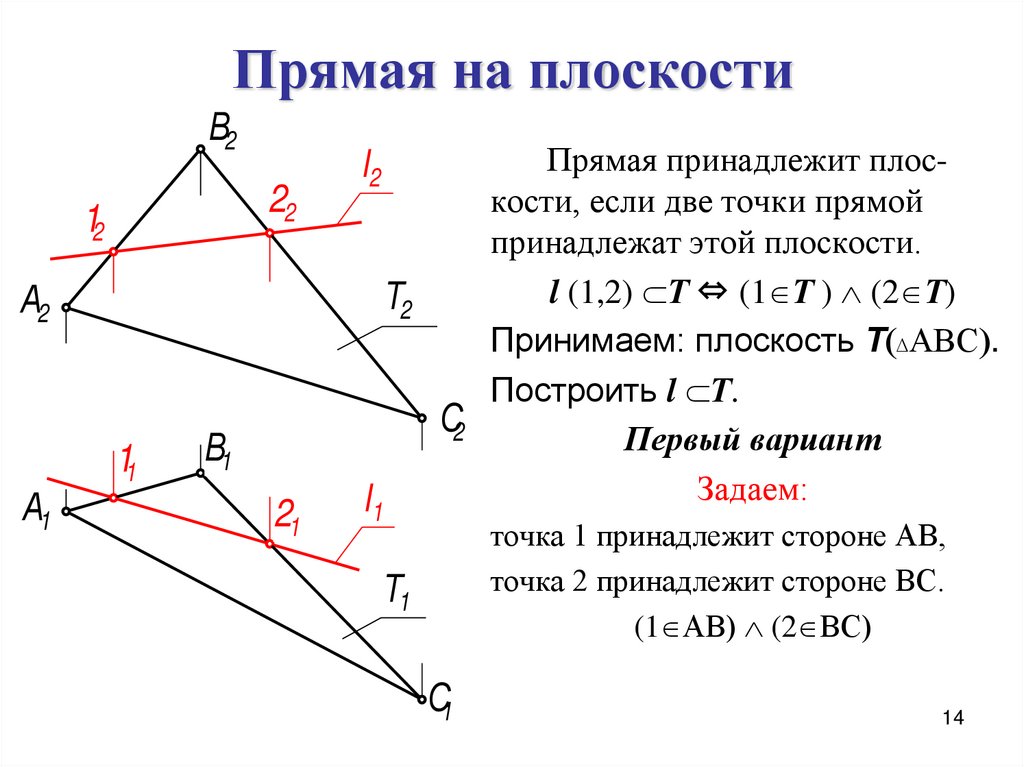
14. Прямая на плоскости

В2
22
12
l2
Т2
А2
А1
11
В1
21
l1
Прямая принадлежит плоскости, если две точки прямой
принадлежат этой плоскости.
l (1,2) Т ⇔ (1 Т ) (2 Т)
Принимаем: плоскость Т АВС .
Построить l Т.
С2
Первый вариант
Задаем:
точка 1 принадлежит стороне АВ,
точка 2 принадлежит стороне ВС.
(1 АВ) (2 ВС)
Т1
С1
14

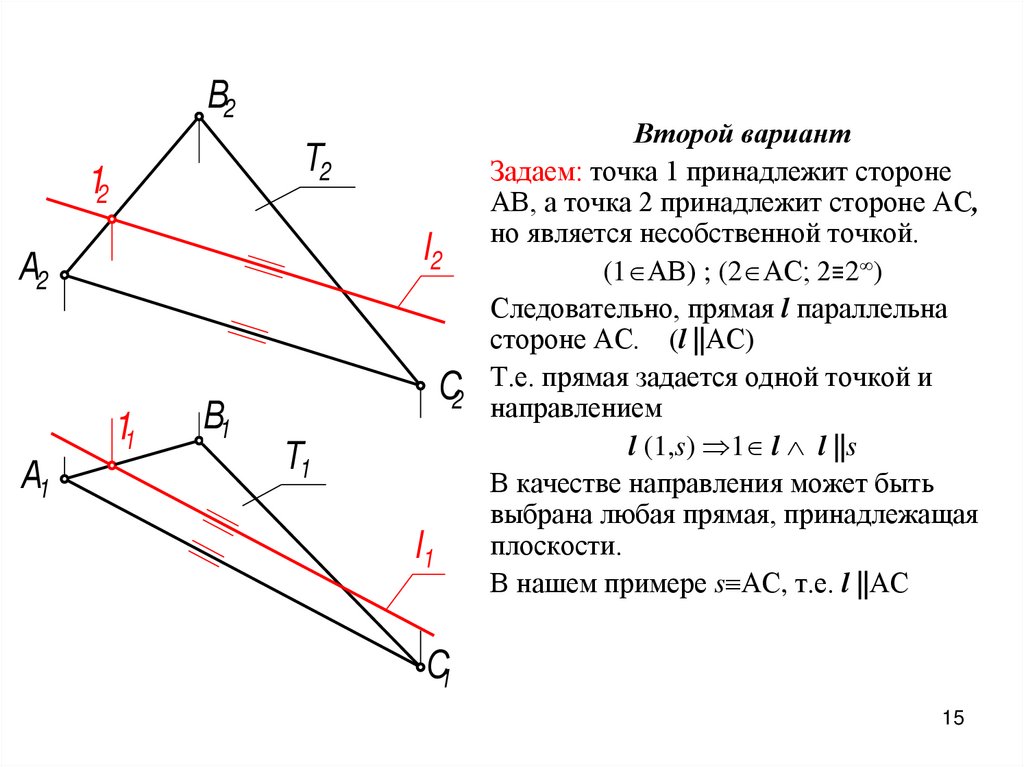
15.

В2
Т2
12
А2
А1
11
В1
Т1
Второй вариант
Задаем: точка 1 принадлежит стороне
АВ, а точка 2 принадлежит стороне АС,
l2 но является несобственной точкой.
(1 АВ) ; (2 АС; 2≡2∞)
Следовательно, прямая l параллельна
стороне АС. (l ||АС)
прямая задается одной точкой и
С2 Т.е.
направлением
l (1,s) 1 l l ||s
В качестве направления может быть
выбрана любая прямая, принадлежащая
l1 плоскости.
В нашем примере s АС, т.е. l ||АС
С1
15

16. Главные линии плоскости

К главным линиям плоскости относятся
прямые уровня - горизонталь, фронталь,
профильная прямая, и линии наибольшего
наклона плоскости.
16

17. Прямые уровня плоскости

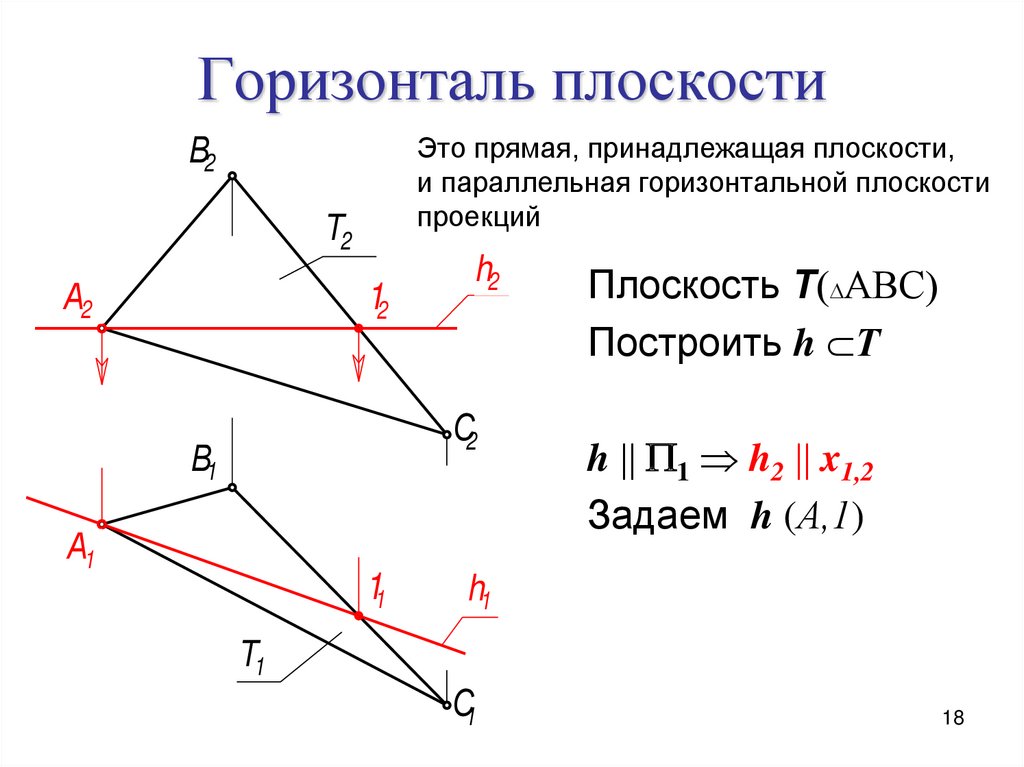
17

18. Горизонталь плоскости

В2
Это прямая, принадлежащая плоскости,
и параллельная горизонтальной плоскости
проекций
Т2
А2
12
h2
С2
В1
А1
11
Плоскость Т АВС
Построить h Т
h 1 h2 x1,2
Задаем h (А,1)
h1
Т1
С1
18

19. Фронталь плоскости

В2
12
Это прямая, принадлежащая плоскости,
и параллельная фронтальной плоскости
проекций
f2
А2
Плоскость Т АВС
Построить f Т
Т2
В1
А1
С2
f 2 f1 x1,2
Задаем f (А,1)
11
f1
Т1
С1
19

20. Линии наибольшего наклона плоскости

Данные линии применяются для определения величины угла наклона плоскости к
какой-либо плоскости проекций.
В частности, линия наибольшего наклона
плоскости, используемая для определения
угла наклона к горизонтальной плоскости
проекций, получила название линии
наибольшего ската плоскости.
20

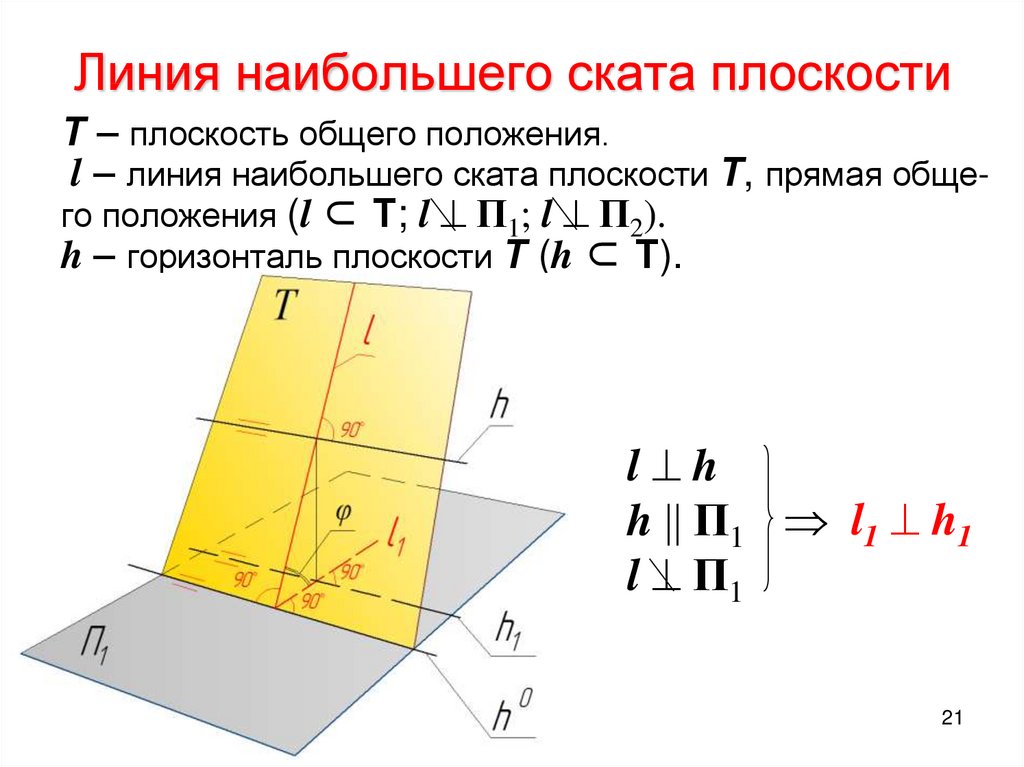
21. Линия наибольшего ската плоскости

Т – плоскость общего положения.
l – линия наибольшего ската плоскости Т, прямая общего положения (l ⊂ Т; l П1; l П2).
h – горизонталь плоскости Т (h ⊂ Т).
l h
h П1 l1 h1
l П1
21

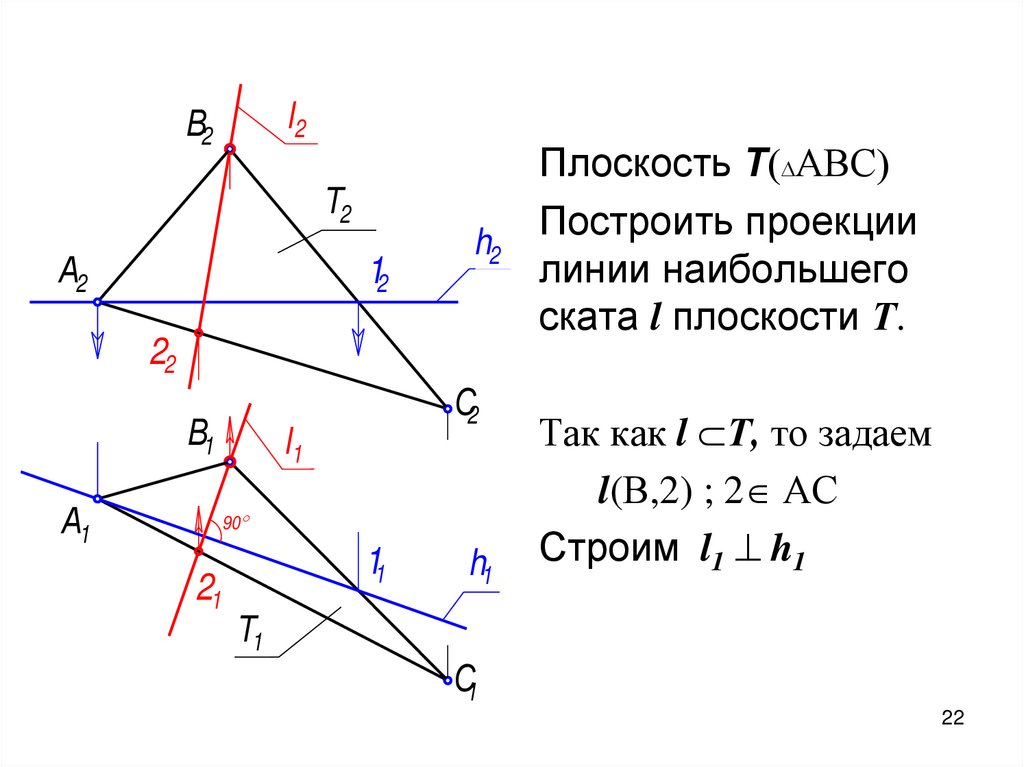
22.

l2
В2
Т2
А2
12
h2
22
В1
А1
С2
l1
90
21
11
h1
Плоскость Т АВС
Построить проекции
линии наибольшего
ската l плоскости Т.
Так как l Т, то задаем
l(В,2) ; 2 АС
Строим l1 h1
Т1
С1
22

23. Точка на плоскости

23

24.

Точка принадлежит плоскости,
если она принадлежит прямой,
принадлежащей этой плоскости
А Ф А l,l Ф
24

25.

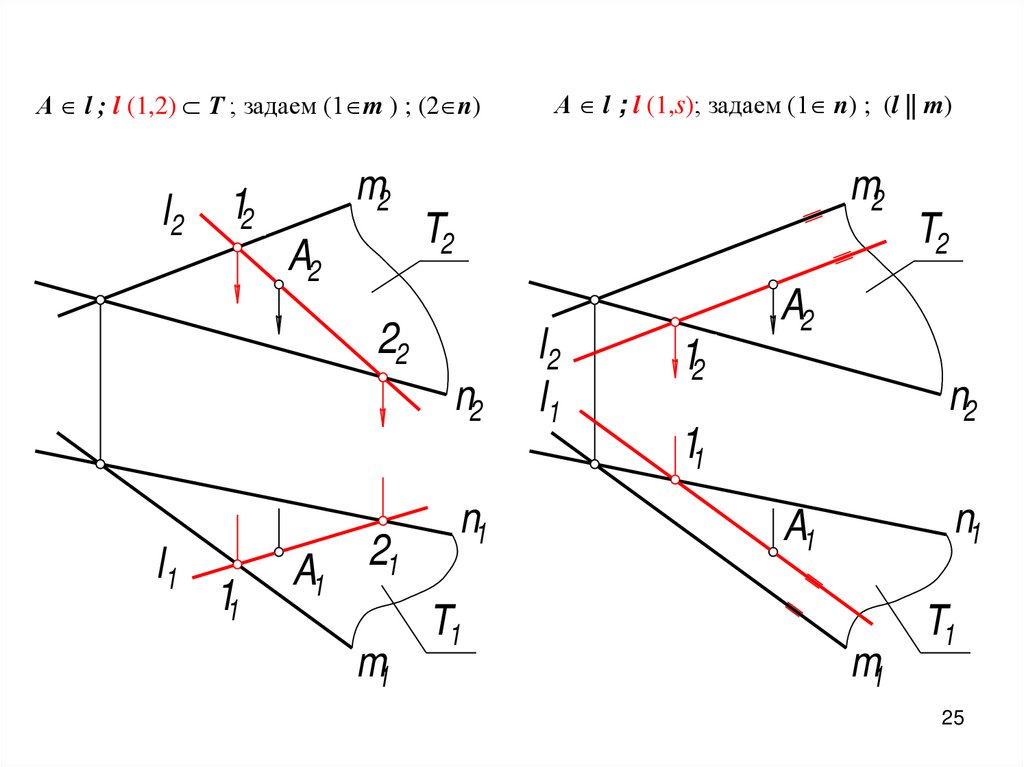
А l ; l (1,2) Т ; задаем (1 m ) ; (2 n)
l2
m2
12
A2
m2
Т2
22
n2
l1
11
A1
21
m1
А l ; l (1,s); задаем (1 n) ; (l || m)
n1
Т1
l2
l1
Т2
A2
12
n2
11
n1
A1
m1
Т1
25

26. Взаимное положение двух плоскостей

26

27. Параллельные плоскости

27

28.

T2T2
a2a2
d2d2
b2b2
T1T1
a1a1
P1P1
c1c1
b1b1
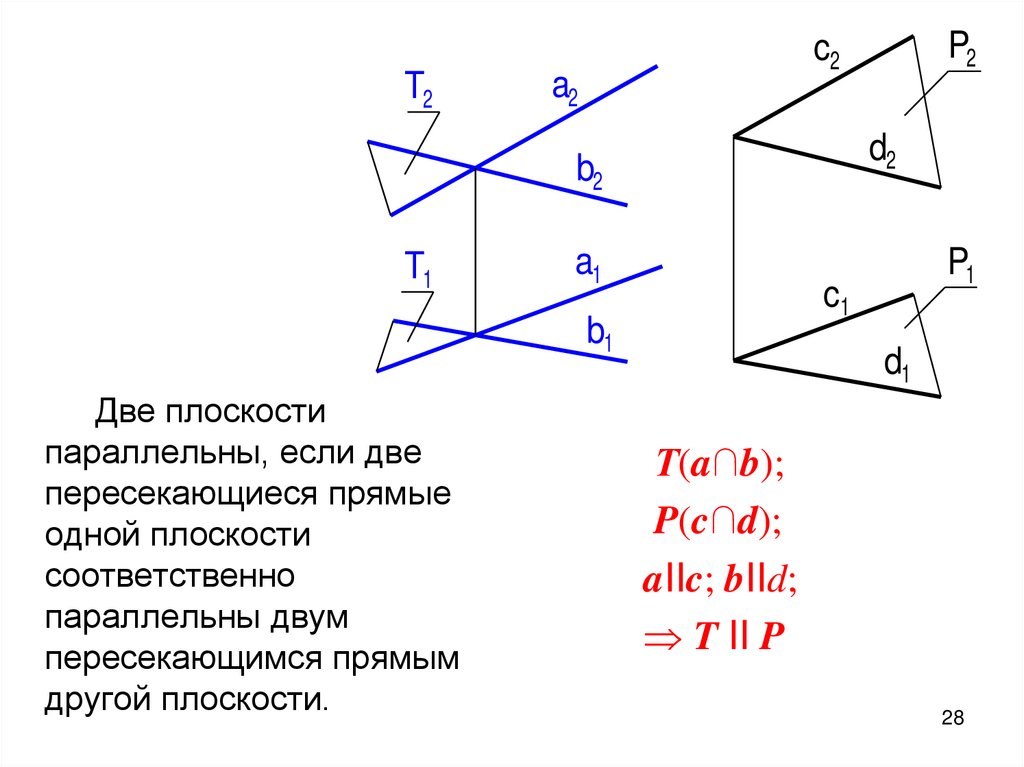
Две плоскости
параллельны, если две
пересекающиеся прямые
одной плоскости
соответственно
параллельны двум
пересекающимся прямым
другой плоскости.
P2P2
c2c2
d1d1
Т(a∩b);
P(c∩d);
aIIc; bIId;
T II P
28

29. Пересекающиеся плоскости

29

30.

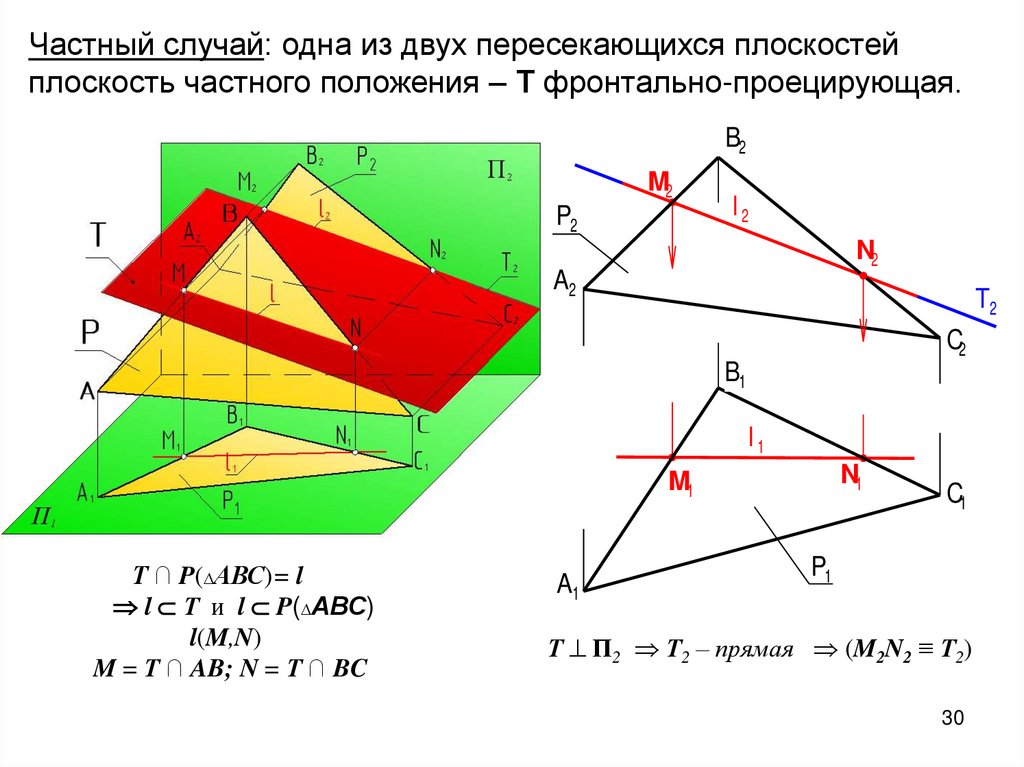
Частный случай: одна из двух пересекающихся плоскостей
плоскость частного положения – Т фронтально-проецирующая.
B2
M2
P2
l2
N2
A2
T2
C2
B1
l1
N1
M1
Т ∩ P(∆АВС)= l
l Т и l P(∆АВС)
l(M,N)
M = Т ∩ AB; N = Т ∩ BC
A1
C1
P1
Т П2 Т2 – прямая (M2N2 ≡ Т2)
30

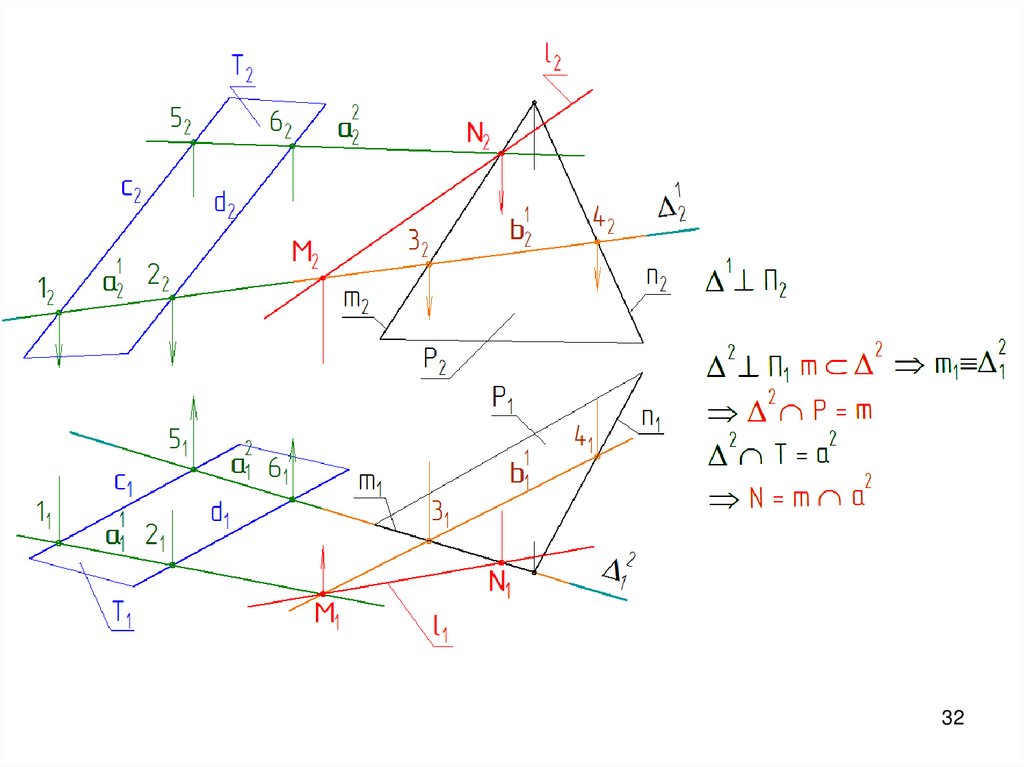
31.

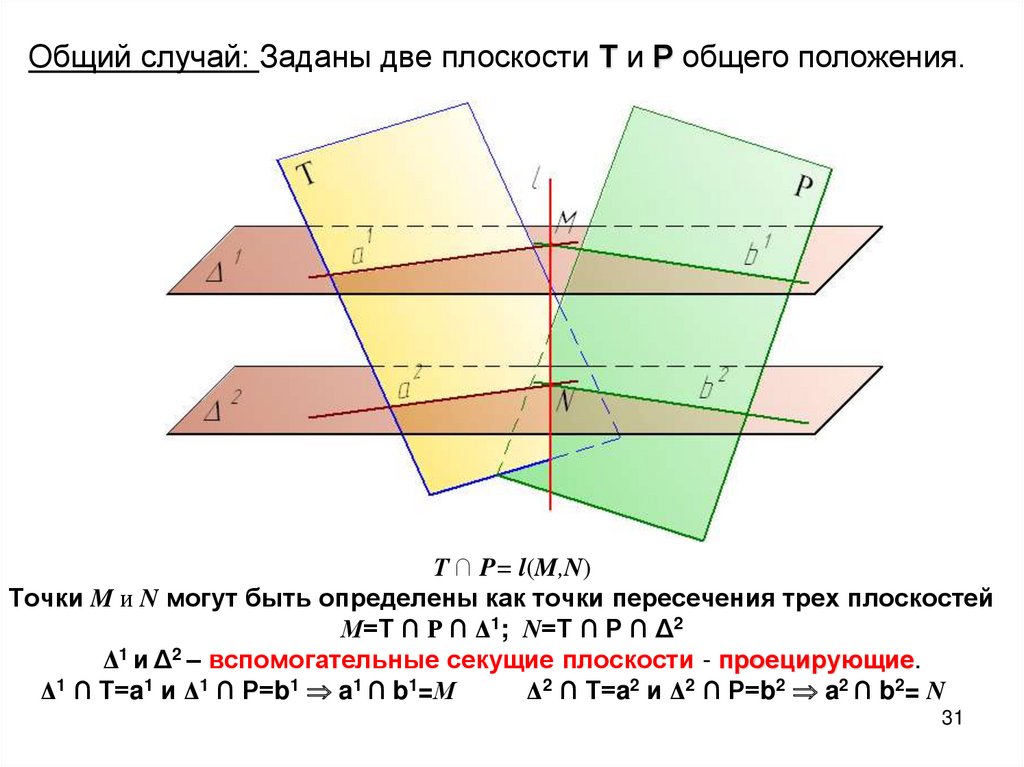
Общий случай: Заданы две плоскости Т и Р общего положения.
Т ∩ P= l(M,N)
Точки M и N могут быть определены как точки пересечения трех плоскостей
М=Т ∩ Р ∩ Δ1; N=Т ∩ Р ∩ Δ2
Δ1 и Δ2 – вспомогательные секущие плоскости - проецирующие.
Δ1 ∩ Т=a1 и Δ1 ∩ Р=b1 a1 ∩ b1=М
Δ2 ∩ Т=a2 и Δ2 ∩ Р=b2 a2 ∩ b2= N
31

32.

32

33. Взаимное положение прямой линии и плоскости

33

34.

Прямая по отношению к плоскости
может занимать следующие положения:
• Принадлежать;
• Быть параллельной;
• Пересекать;
• Быть перпендикулярной.
34

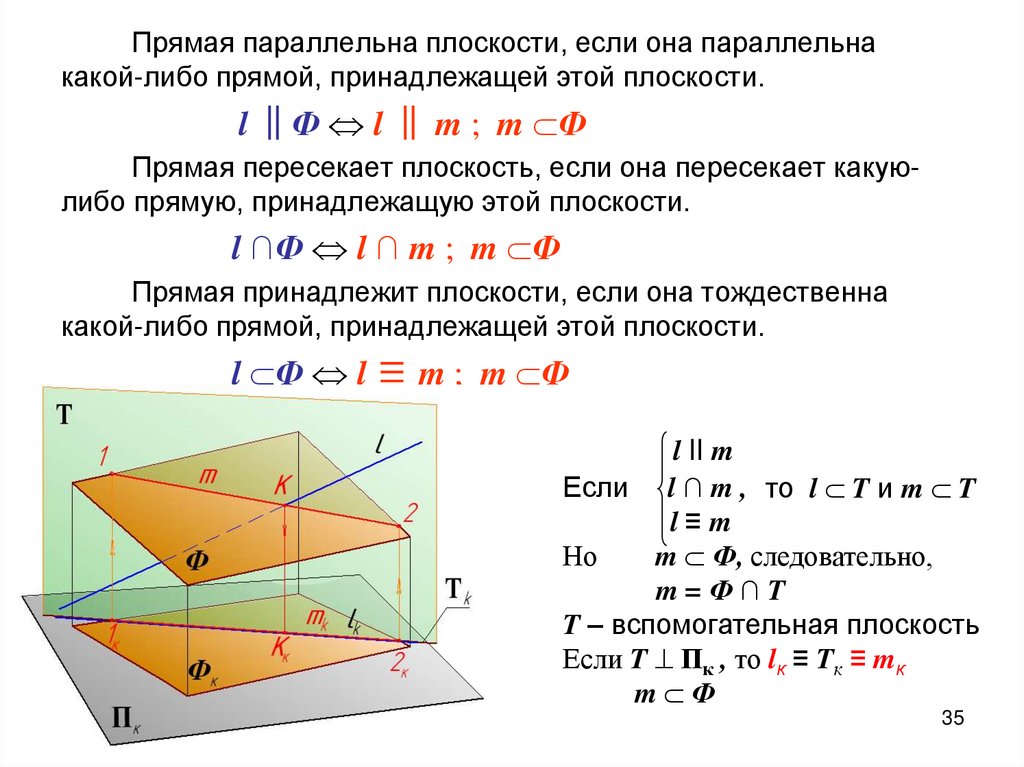
35.

Прямая параллельна плоскости, если она параллельна
какой-либо прямой, принадлежащей этой плоскости.
l ‖Ф l ‖ m ; m Ф
Прямая пересекает плоскость, если она пересекает какуюлибо прямую, принадлежащую этой плоскости.
l ∩Ф l ∩ m ; m Ф
Прямая принадлежит плоскости, если она тождественна
какой-либо прямой, принадлежащей этой плоскости.
l Ф l ≡ m ; m Ф
l II m
Если l ∩ m , то l T и m T
l≡m
Но
m Ф, следовательно,
m=Ф∩T
T – вспомогательная плоскость
Если T Пк , то lк ≡ Tк ≡ mк
m Ф
35

36. Последовательность действий при определении взаимного положения прямой линии и плоскости

Пример. Заданы прямая l и плоскость Ф( АВС).
1. Одну из проекций заданной прямой l, которую
условно будем называть первой, совместить с
одноименной
проекцией
вспомогательной
прямой, например m. Прямую m нужно
рассматривать как принадлежащую заданной
плоскости Ф( АВС).
lk≡ mk ; k =1, 2; m Ф ( АВС)
На рисунке l1≡ m1
2. Построить недостающую (условно вторую)
проекцию вспомогательной прямой m.
если (m1≡ l1) то строиться m2;
если (m2≡ l2) то строиться m1.
3. На построенной (условно второй) проекции
определить взаимное положение прямой l и
вспомогательной прямой m.
если (m≡ l), то l Ф,
если (m ‖ l), то l ‖Ф,
если (m ∩ l), то l ∩Ф
На примере (l ∩ m=К, К= l ∩Ф ).
36

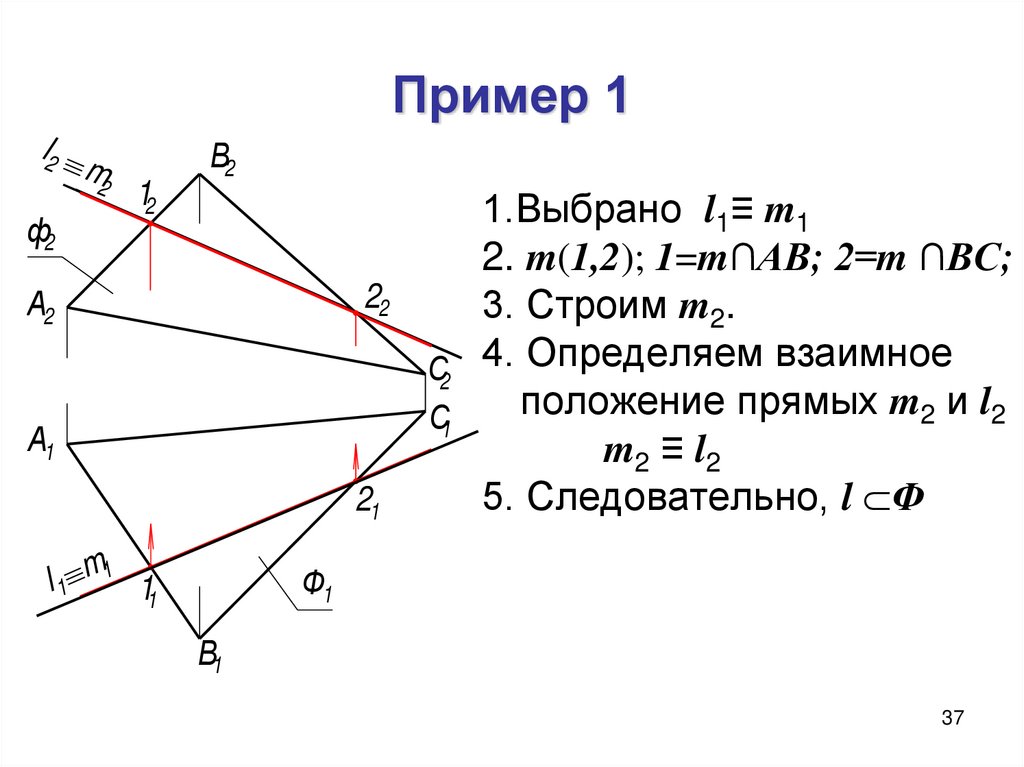
37. Пример 1

l2
ф2
m2
12
В2
22
А2
А1
21
l 1 m1 11
1.Выбрано l1≡ m1
2. m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. Строим m2.
С2 4. Определяем взаимное
положение прямых m2 и l2
С1
m2 ≡ l2
5. Следовательно, l Ф
Ф1
В1
37

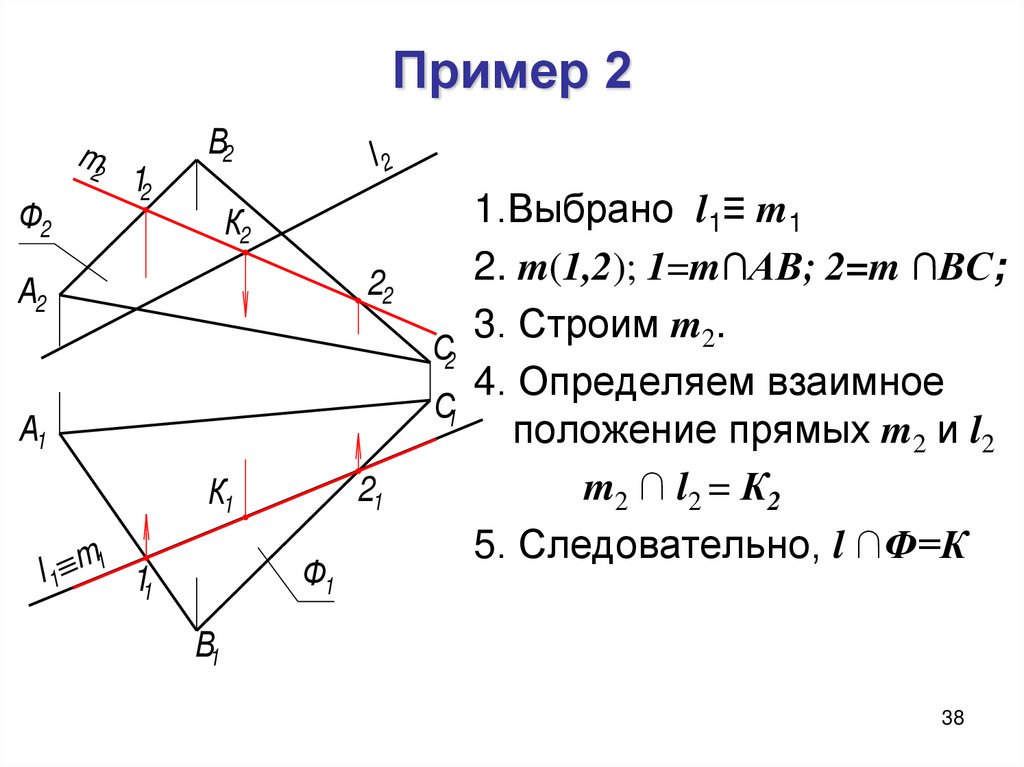
38. Пример 2

m2
Ф2
12
В2
l2
К2
22
А2
А1
К1
l 1 m1 11
21
Ф1
1.Выбрано l1≡ m1
2. m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. Строим m2.
С2
4. Определяем взаимное
С1
положение прямых m2 и l2
m2 ∩ l2 = К2
5. Следовательно, l ∩Ф=К
В1
38

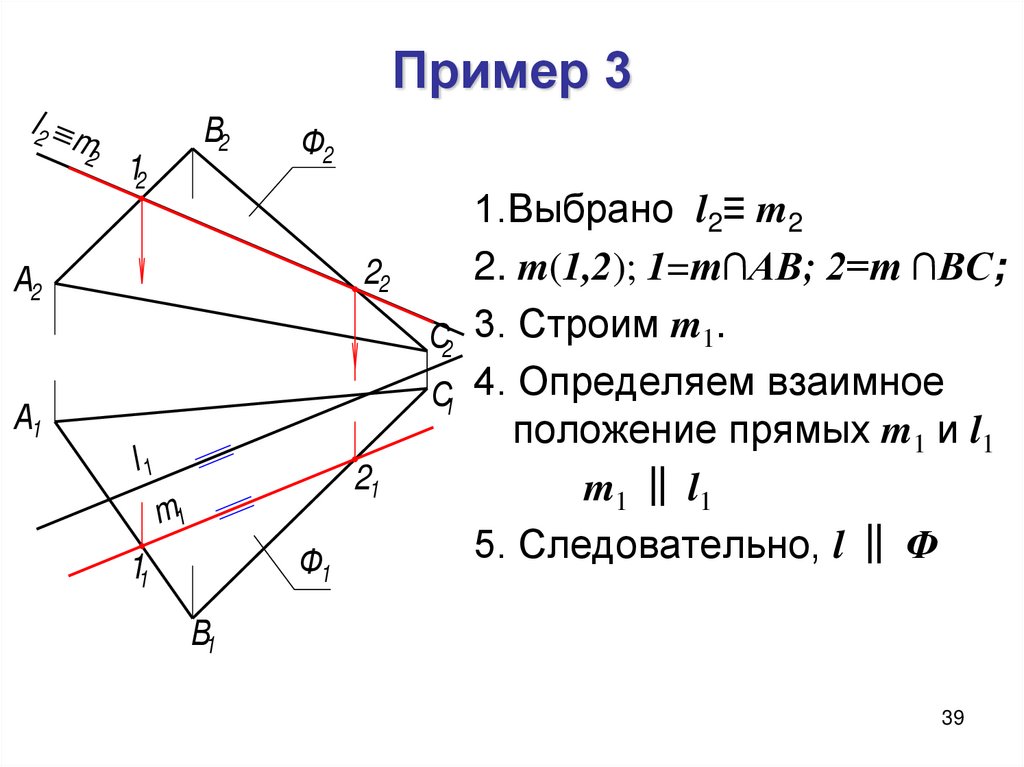
39. Пример 3

l2 m
2
В2
12
Ф2
22
А2
А1
l1
21
m1
Ф1
11
1.Выбрано l2≡ m2
2. m(1,2); 1=m∩АВ; 2=m ∩ВС;
С2 3. Строим m1.
С1 4. Определяем взаимное
положение прямых m1 и l1
m1 ‖ l1
5. Следовательно, l ‖ Ф
В1
39

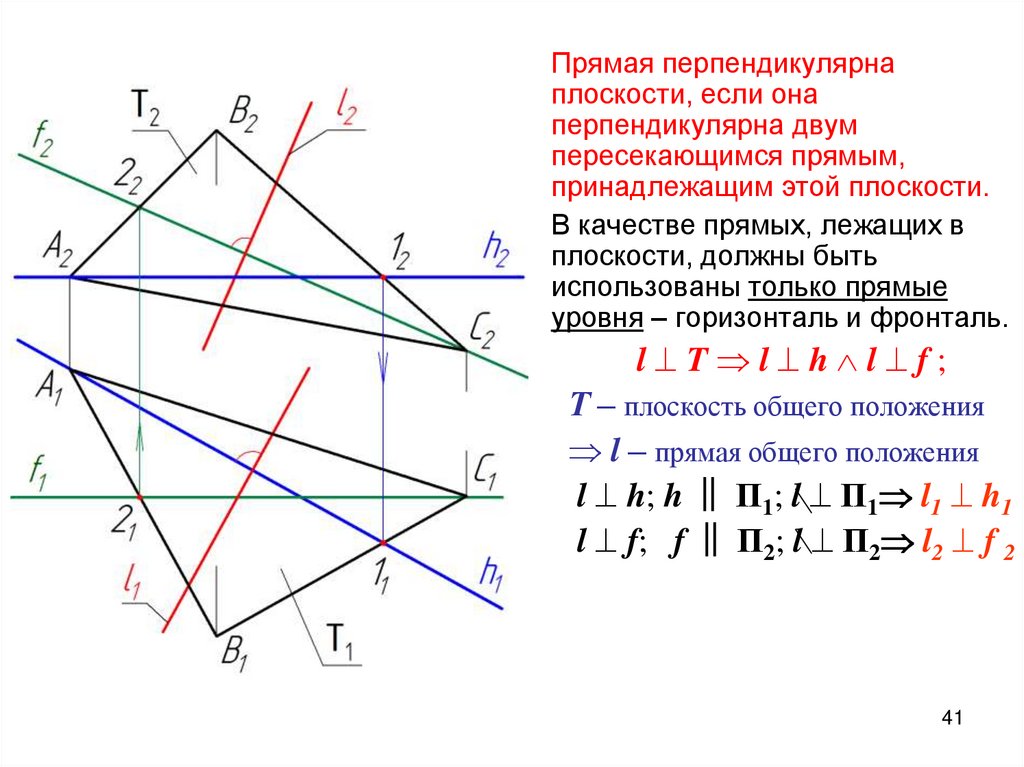
40. Прямая перпендикулярная плоскости

40

41.

Прямая перпендикулярна
плоскости, если она
перпендикулярна двум
пересекающимся прямым,
принадлежащим этой плоскости.
В качестве прямых, лежащих в
плоскости, должны быть
использованы только прямые
уровня – горизонталь и фронталь.
l T l h l f;
Т – плоскость общего положения
l – прямая общего положения
l h; h ‖ П1; l П1 l1 h1
l f; f ‖ П2; l П2 l2 f 2
41

42. Взаимно перпендикулярные плоскости

42

43.

Две плоскости взаимно
перпендикулярны, если
одна из плоскостей
содержит (проходит через)
прямую, перпендикулярную
другой плоскости.
Через точку D провести
плоскость Р перпендикулярную
плоскости Т( АВС).
Р(l∩m); l ∩ m = D
Строим l T (D l; l1 h1; l2 f2)
Строим прямую m (D m).
Задаем
43