Элементы математического анализа

1. Элементы математического анализа

Лектор: Войтик Виталий
Викторович

2.

3.

f(x0 + x)

4.

5. Замечательные пределы

• Первый замечательный предел:
sin x
lim
1
x 0
x
• Второй замечательный предел:
x
1
lim 1 lim 1 x e 2, 718
x
x 0
x
1
x

6.

7.

8. Геометрический смысл производной

9.

10.

11.

Производные основных элементарных функций.
1)С = 0;
2)(xm) = mxm-1;
1
3)
x
2 x
1
1
4) 2
x
x
5) e x e x
6) a
x
a ln a
x
1
7) ln x
x
8) log a x
9) sin x cos x
10) cos x sin x
1
11) tgx
cos 2 x
12) ctgx
13) arcsin x
14) arccos x
1
x ln a
1
sin 2 x
1
1 x2
1
1 x2
1
15) arctgx
1 x2
1
16) arcctgx
1 x2

12.

Производная сложной функции.
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в
область определения функции f.
Тогда
y f (u ) u
Пример. Найти производную функции
.
1
2
y x cos x sin x cos x
2
Сначала преобразуем данную функцию:
x
1
y sin 2 x cos 2 x
2
2
1
1
1
y sin 2 x x 2 cos 2 x 2 cos x ( sin x)
2
2
2

13.

1
y sin 2 x x cos 2 x sin x cos x x cos 2 x.
2

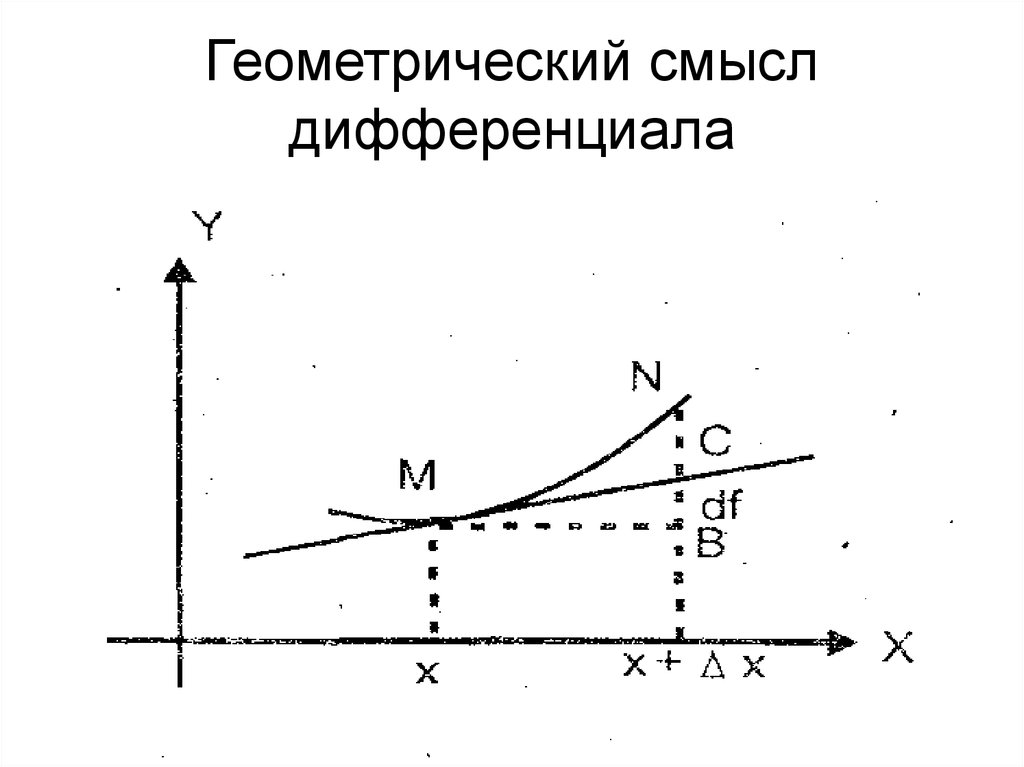
14. Геометрический смысл дифференциала

15. Связь между дифференциалом функции и её приращением Дифференциал

16.

• Дифференциал k-ого порядка

17. Функции нескольких переменных

• Величину z называют функцией двух
переменных x и y, если каждой паре
допустимых значений этих переменных
соответствует одно определённое значение
величины z.

18. Частные производные функций

19. Частные и полный дифференциал функции

20. Применение дифференциала для приближенных вычислений.

Из определения производной функции:
Можно записать:
,
или
.
Величина αΔx - бесконечно малая более высокого
порядка, чем f’(x)Δx, т.е. f'(x)Δx- главная часть
приращения у. Отбрасывая вторую часть в этой
формуле, можем написать: Δy=f’(x)Δx
или f(x+Δx)-f(x)=f’(x)Δx; отсюда можем вычислить
значение функции в точке x+Δx: f(x+Δx)=f(x)+f’(x)Δx;
если f(х) и f’(x) можно легко вычислить в точке x.

21.

22. Пример: вычислить Sin29 ͦ

Sin29 ͦ=Sin(30 ͦ-1 ͦ), поэтому примем x=30 ͦ, а Δx=-1 ͦ.
1 ͦ=3,14/180=0,017
Sin’x=Cosx
Sin29 ͦ=Sin30 ͦ+Cos30 ͦ(-0,017)=0,485.
• Пример: Вычислите lg101.
• Примем x=100, а Δx=1
• (lgx)’=1/x ln10
1
0,01
lg 101 lg 100 1
2
2,0043
100 ln 10
2,302

23. Применение дифференциала функции в приближённых вычислениях Задача: найдите абсолютную погрешность в определении объема

цилиндра, если при
измерениях были получены радиус r= (6±0,1) см а
высота h=(10±0,2) cм.