Равновесие плоской системы параллельных сил

1. Теоретическая механика Статика

Лекция № 3

2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ

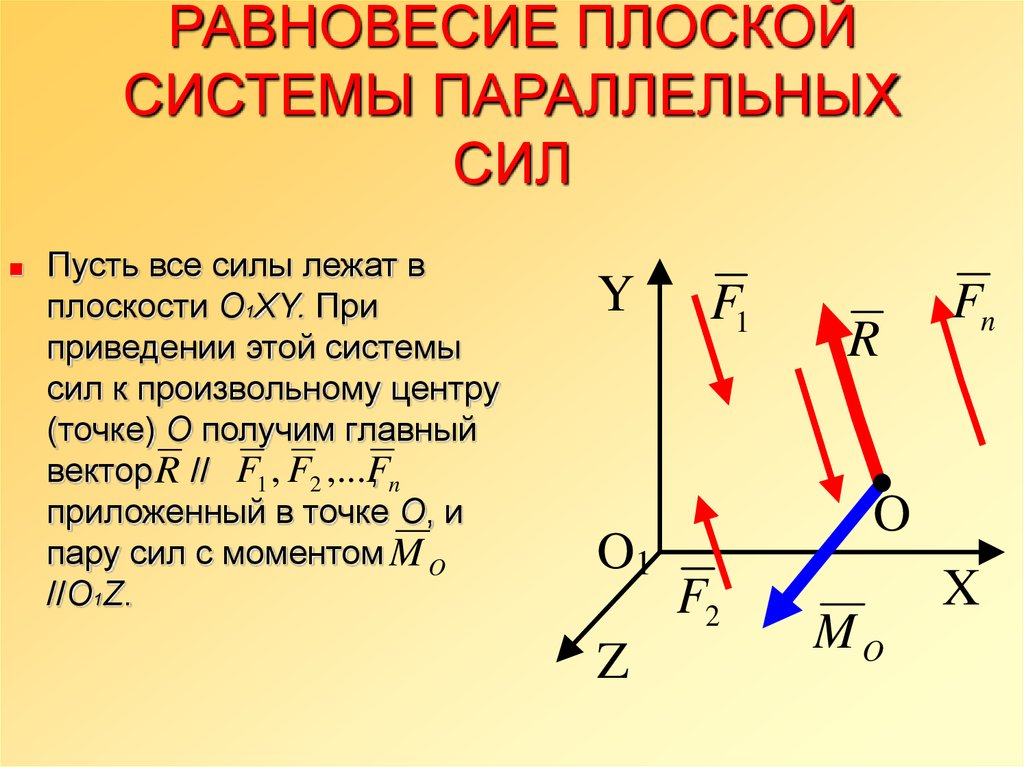
Пусть все силы лежат в
плоскости О1XY. При
приведении этой системы
сил к произвольному центру
(точке) О получим главный
вектор R // F1 , F2 ,...F
,n
приложенный в точке О, и
пару сил с моментом M O
//O1Z.
Y
O1
Z
F1
R
Fn
O
F2
MO
X

3.

Расположим ось О1Y
параллельно силам F1 , F2 , Fn ,
тогда вектор M O
перпендикулярен
плоскости О1XY и его
можно считать величинойY
алгебраической
Из условия R 0; M O 0
следуют две формы
аналитических условий
равновесия
плоской системы
параллельных сил.
F1
R
MO O
F2
O1
Fn
X

4. Основная форма условий равновесия

Для равновесия плоской системы
параллельных сил необходимо и
достаточно, чтобы сумма проекций всех
сил на ось О1Y, параллельную им, и
сумма их моментов относительно
любой точки О, лежащей в плоскости
действия сил О1XY, были равны нулю.
F
kY
0; M O 0
точка О любая в плоскости О1 XY

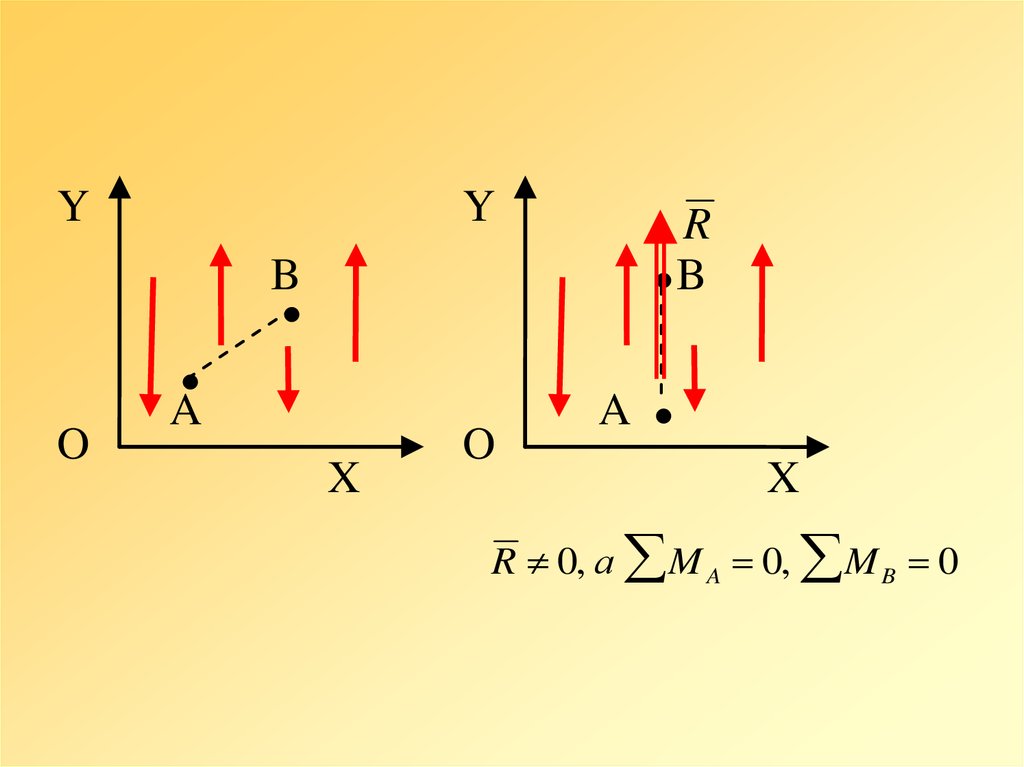
5. Вторая форма условий равновесия:

Для равновесия плоской системы
параллельных сил необходимо и
достаточно, чтобы суммы моментов
всех сил относительно любых двух
точек А и В (причем прямая АВ не
параллельна силам), были равны
нулю
M
A
0; M B 0;
AB не паралльна силам

6.

Y
Y
R
B
B
O
A
X
O
A
X
R 0, а M A 0, M B 0

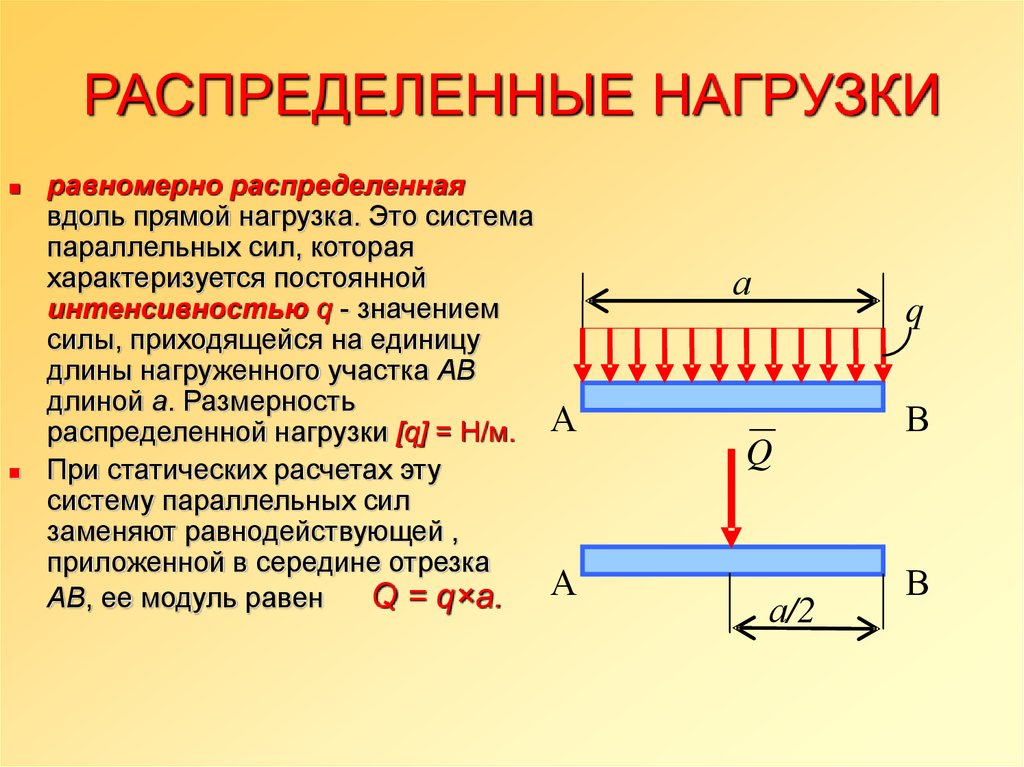
7. РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ

равномерно распределенная
вдоль прямой нагрузка. Это система
параллельных сил, которая
характеризуется постоянной
интенсивностью q - значением
силы, приходящейся на единицу
длины нагруженного участка АВ
длиной а. Размерность
распределенной нагрузки [q] = H/м.
При статических расчетах эту
систему параллельных сил
заменяют равнодействующей ,
приложенной в середине отрезка
АВ, ее модуль равен
Q = q×a.
а
А
А
q
Q
а/2
В
В

8.

Неравномерно
распределенная нагрузка.
Параллельные силы
увеличиваются от нуля до
qmax по линейному закону.
Равнодействующая таких сил
по модулю равна площади A
треугольника АВС,
Q = 0,5×qmax×a.
Линия действия
равнодействующей силы
проходит через центр тяжести
треугольника, т. е. на
расстоянии a/3 от точки В.
a
Cq
max
B
Q
a/3

9. РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ

Связи между частями конструкции
называются внутренними (шарнир С),
скрепляющие конструкцию с другими телами,
- внешними (шарниры А и В).

10.

Для определения внутренних и внешних
реакций связей трех шарнирной арки
расчленим конструкцию по
соединительному шарниру С на две части
и рассмотрим равновесие каждой из
частей в отдельности.

11.

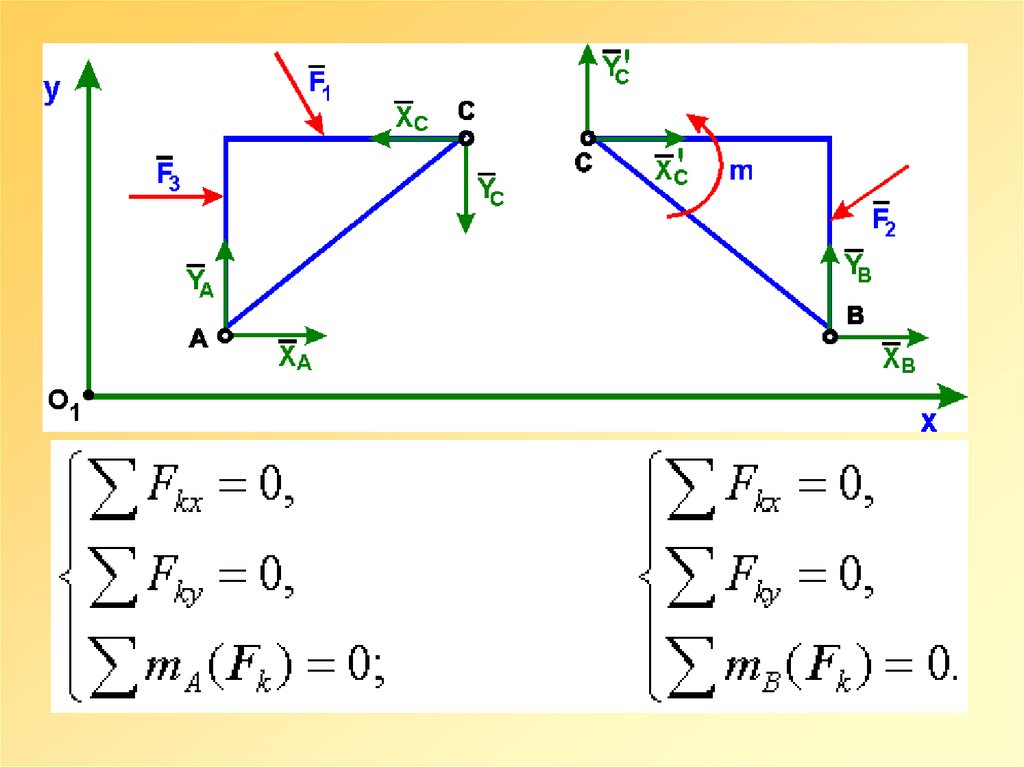
При действии на трех шарнирную арку
заданной произвольной плоской
системы сил для каждой части можно
записать по три уравнения равновесия:
для АС
дляСВ

12. Статически определимые системы тел

Системы тел (тело), для которых число
неизвестных реакций связей равно числу
уравнений равновесия, называются
статически определимыми. Если число
неизвестных реакций связей больше
числа уравнений равновесия (на одно, два
и т.д.), то системы тел называются
статически неопределимыми
(соответственно один, два и т.д. раза). Такие
задачи невозможно решить методами
статики.

13.

14. Проверка решения задачи

Для проверки решения задачи
считают всю конструкцию отвердевшей
(принцип отвердевания, аксиома 5, §1).
В точке С две части конструкции
соединены жестко. Реакции в этой точке
отсутствуют.

15.

Графическая
проверка
Строят в масштабе
силовой
многоугольник. Если
многоугольник
замкнут, то задача
решена верно.
Аналитическая
проверка
Составляют одно два уравнения
равновесия для
конструкции в
целом. Если
проверочные
уравнения
равновесия
обращаются в
тождества, то
задача решена
верно.