Плоская произвольная система сил. Лекция 4СЭн

1.

Лекция 4СЭ
1
Плоская произвольная система сил
1. Приведение плоской произвольной системы сил.
Главный вектор плоской произвольной системы сил расположен в
плоскости сил, а главный момент перпендикулярен к ней, MO R, рис.4.
Расчет главного вектора и главного момента ведется по формулам:
Rx = Fix , Ry = Fiy .
R R R .
MO = MiO = (xiFiy – yiFix).
2
x
2
y
Ry
R
cos R x , cos R
.
R
R
z
MO
O
y
R
x
Рис. 1
2. Условия равновесия плоской произвольной системы сил.
Rx = Fix= 0 , Ry = Fiy= 0, MO = MiO= 0.
3. Частные случаи приведения плоской произвольной системы сил.
Главный вектор R лежит в плоскости П, главный момент МO пл. П, рис. 1.
1) К равнодействующей, R ≠ 0, MO = 0.
Теорема Вариньона. Момент равнодействующей
относительно любого центра, расположенного в
плоскости сил, равен алгебраической сумме моментов
всех сил относительно того же центра.
П
Проецируя MO(R) = MO(Fi) (см. лекция 3СЭ, (10)) на ось z П, получим
Mz(R) = Mz(Fi), или MO(R) = MO(Fi), где О – точка пересечения оси z
с плоскостью П, рис. 2.
z
MO(Fi)
O
Рис.2
R

2.

Лекция 4СЭ
2
Плоская произвольная система сил
2) К главному моменту: R = 0, M ≠ 0. При этом величина главного момента не зависит
от центра приведения, так как иначе разные главные моменты были бы эквивалентны
одной и той же системе сил.
3) К главному вектору и главному моменту, причем R MO, рис.3.
Эту систему можно упростить еще более, сведя к равнодействующей.
Представим главный момент MO в виде пары сил (R', R")
такой, что силы R" = -R и расположены на одной прямой.
Силы R и R", как взаимно уравновешенные, можно удалить.
Остается равнодействующая R' = R, приложенная в точке О1.
Плечо d определим по формуле: d = MO /R.
R"
MO
O
R'
R
d
Рис. 3
Вывод: плоская произвольная система сил приводится или к равнодействующей,
или к главному моменту, либо является уравновешенной.
O1

3.

Лекция 4СЭ
3
4. Три формы условий равновесия плоской произвольной системы сил.
I. Fix = 0, Fiy = 0, MO(F) = 0.
II. MA(Fi) = 0, MB(Fi) = 0, MC(Fi) = 0, причем точки А, В и С не должны лежать
на одной прямой. Приняв за центр приведения любую из точек А, В или С, получим, что
главный момент равен нулю. Предположим, что R ≠ 0. Из условия MA(Fi) = 0 и теоремы
Вариньона следует, что MA(R) = 0, то есть равнодействующая R проходит через точку А.
Из условий MB(Fi) = 0 и MC(Fi) = 0 следует, что равнодействующая R проходит также
через точки В и С, что невозможно, если все эти точки не лежат на одной прямой.
III. MA(Fi) = 0, MB(Fi) = 0, Fi = 0, причем ось не прямой АВ. Из первых двух
равенств следует, что главный момент равен нулю. Предположим, что R ≠ 0. По теореме
Вариньона из условий MA(Fi) = 0 и MB(Fi) = 0 следует, что MA(R) = MB(R) = 0, то есть
равнодействующая R проходит через точки А и В. Так как Fi = R = Rcos и угол =
R, ≠ 0, то при cos ≠ 0 из условия Fi = 0 следует, что R = 0.
5. Статически определимые и неопределимые задачи.
Задача является статически определимой, если число неизвестных равно числу
уравнений равновесия. В противном случае задача статически неопределима (не решаема
методами статики). Примеры статически неопределимых задач приведены на рис. 4 и 5.
YA
A
M
XA
R1
R2
YB
B
T1
XB
Рис. 4
T2
T3
N
F1
G
F2
Рис. 5

4.

Лекция 4СЭ
4
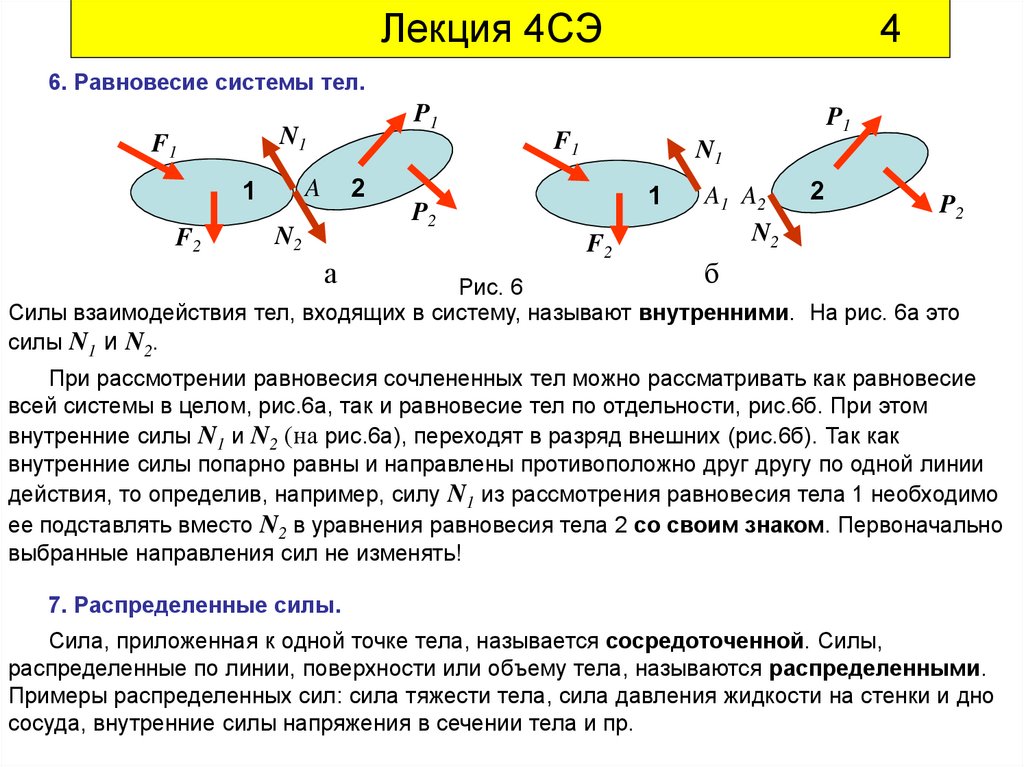
6. Равновесие системы тел.
N1
F1
P1
F1
N1
2
A
1
F2
P1
1
P2
N2
а
F2
A1 A2
N2
2
P2
б
Рис. 6
Силы взаимодействия тел, входящих в систему, называют внутренними. На рис. 6а это
силы N1 и N2.
При рассмотрении равновесия сочлененных тел можно рассматривать как равновесие
всей системы в целом, рис.6а, так и равновесие тел по отдельности, рис.6б. При этом
внутренние силы N1 и N2 (на рис.6а), переходят в разряд внешних (рис.6б). Так как
внутренние силы попарно равны и направлены противоположно друг другу по одной линии
действия, то определив, например, силу N1 из рассмотрения равновесия тела 1 необходимо
ее подставлять вместо N2 в уравнения равновесия тела 2 со своим знаком. Первоначально
выбранные направления сил не изменять!
7. Распределенные силы.
Сила, приложенная к одной точке тела, называется сосредоточенной. Силы,
распределенные по линии, поверхности или объему тела, называются распределенными.
Примеры распределенных сил: сила тяжести тела, сила давления жидкости на стенки и дно
сосуда, внутренние силы напряжения в сечении тела и пр.

5.

Лекция 4СЭ
5
Количественной мерой распределенной силы является ее интенсивность q величина нагрузки на тело в данной его точке. Единицы интенсивности – Н/м, Н/м2, Н/м3.
При решении задач статики распределенную силу заменяют сосредоточенной – ее
равнодействующей. При этом необходимо определить величину и точку приложения этой
равнодействующей.
Рассмотрим пример силы, распределенной по длине балки L = АВ, рис. 7.
Зависимость интенсивности от длины балки графически показана ее эпюрой – q = q(х).
Выделим элемент балки dx на расстоянии х от
начала А. Элементарная сила, приходящаяся на
этот элемент длины, dQ = q(x)dx. Величина
сосредоточенной силы Q равна:
Q
х
dx q = q(x)
эпюра
С
A
L
Q q( x)dx.
q
B
l
(1)
Рис.7
0
Из (1) следует, что сила Q численно равна площади эпюры.
Точку приложения силы Q найдем по теореме Вариньона: MA(Q) = MA(dQ), или
L
L
Ql xq( x)dx,
0
откуда
xq( x)dx
l 0
Q
. (2)
Из (2) следует, что сила Q проходит через центр тяжести эпюры С.
х

6. Лекция 4СЭ 6

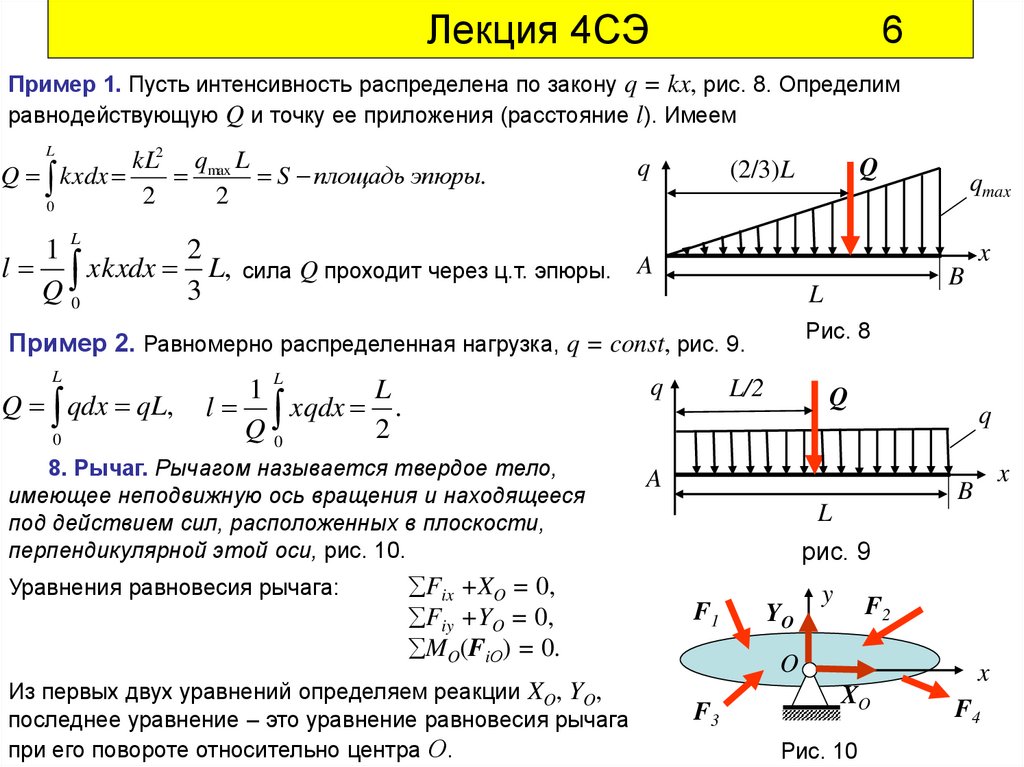
Пример 1. Пусть интенсивность распределена по закону q = kx, рис. 8. Определим
равнодействующую Q и точку ее приложения (расстояние l). Имеем
L
kL2 qmax L
Q kxdx
S площадь эпюры.
2
2
0
q
Q
(2/3)L
qmax
L
1
2
l x kxdx L, сила Q проходит через ц.т. эпюры. A
Q0
3
x
Рис. 8
Пример 2. Равномерно распределенная нагрузка, q = const, рис. 9.
L
Q qdx qL,
0
L
q
1
L
l xqdx .
Q0
2
8. Рычаг. Рычагом называется твердое тело,
имеющее неподвижную ось вращения и находящееся
под действием сил, расположенных в плоскости,
перпендикулярной этой оси, рис. 10.
Уравнения равновесия рычага:
Fix +XO = 0,
Fiy +YO = 0,
MO(FiО) = 0.
Из первых двух уравнений определяем реакции XO, YO,
последнее уравнение – это уравнение равновесия рычага
при его повороте относительно центра О.
B
L
L/2
Q
q
A
x
B
L
рис. 9
F1
YO
y
F2
O
F3
XO
Рис. 10
x
F4