Similar presentations:
Произвольная плоская система сил
1.
СТАТИКА5. Произвольная плоская система сил
2. 5.1. Приведение произвольной плоской системы сил к простейшему виду
Опр. Произвольной плоской системой сил называется такаясистема, линии действия которых лежат в одной плоскости.
Примечание. Частным случаем произвольной плоской системы
сил является плоская система сходящихся сил.
Теорема о приведении произвольной плоской
системы сил к простейшему виду.
Любая плоская система сил, действующих на абсолютно
твердое тело, при приведении к произвольно выбранному
центру О заменяется одной силой R равной главному вектору,
и приложенной в центре приведения О, и одной парой с
моментом М О , равным алгебраической сумме моментов всех
сил относительно центра О, то есть:
R Fk ,
M O mO ( Fk ).
3.
Примечание. Главный момент М О , для плоской системысил заменен на алгебраическую сумму моментов всех сил
относительно центра приведения, так как все векторные
моменты сил будут параллельны.
5.2. Равновесие произвольной плоской системы сил
Необходимые и достаточные условия равновесия любой
системы сил ранее были получены в виде формул (*):
R 0 , M 0 0.
Из этих выражений вытекают аналитические условия
равновесия плоской системы сил. Их можно получить в трех
различных формах.
1. Основная форма условий равновесия
∑ Fkх
= 0, ∑ Fkу = 0, mO ( Fk ) 0.
(1)
4.
Вывод Формулы (1) выражают следующие аналитическиеусловия равновесия: для равновесия произвольной плоской
системы сил необходимо и достаточно, чтобы сумма
проекций всех сил на две координатные оси и сумма
моментов относительно любого центра, лежащего в
плоскости действия сил, были равны нулю.
2. Вторая форма условий равновесия.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы сумма моментов всех этих сил
относительно каких-нибудь двух центров А
А
и В и сумма их проекций на ось Ох, не
перпендикулярную прямой АВ, были равны
О
нулю:
∑ Fkх = 0, m А ( Fk ) 0, mВ ( Fk ) 0.
В
F
х
(2)
5.
3. Третья форма условий равновесия (уравнения 3-х моментов)Для равновесия произвольной плоской системы сил необходимо
и достаточно, чтобы суммы моментов всех этих сил
относительно любых трех центров А, В и С, не лежащих на
одной прямой, были
равны нулю:
(3)
mА (Fk ) 0, mВ ( Fk ) 0, mС ( Fk ) 0.
Равновесие плоской системы параллельных сил
В случае, когда все действующие на тело силы параллельны
друг другу, можно направить ось Ох перпендикулярно
силам, а ось Оу параллельно им.
Тогда первое уравнение в выражении (1)
обратиться в тождество вида 0 ≡ 0. В
результате для параллельных сил
останется только два условия
равновесия
∑ Fkу = 0, m А ( Fk ) 0 ,
у
F1
О
F2
х
Fn
6.
Другая форма условий равновесия для параллельных сил,получающаяся из равенств (2) или (3), имеет вид
m А ( Fk ) 0,
mВ (Fk ) 0.
5.3. Решение задач на равновесие произвольной
плоской системы сил.
Реакции неподвижной шарнирной опоры и жесткой заделки.
В технике часто встречаются задачи с тремя типами
опорных закреплений: подвижная шарнирная опора,
неподвижная шарнирная опора и жесткая заделка. Реакции
этих опор были рассмотрены ранее.
Рассмотрим опорные реакции неподвижной шарнирной
опоры и жесткой заделки подробнее.
7.
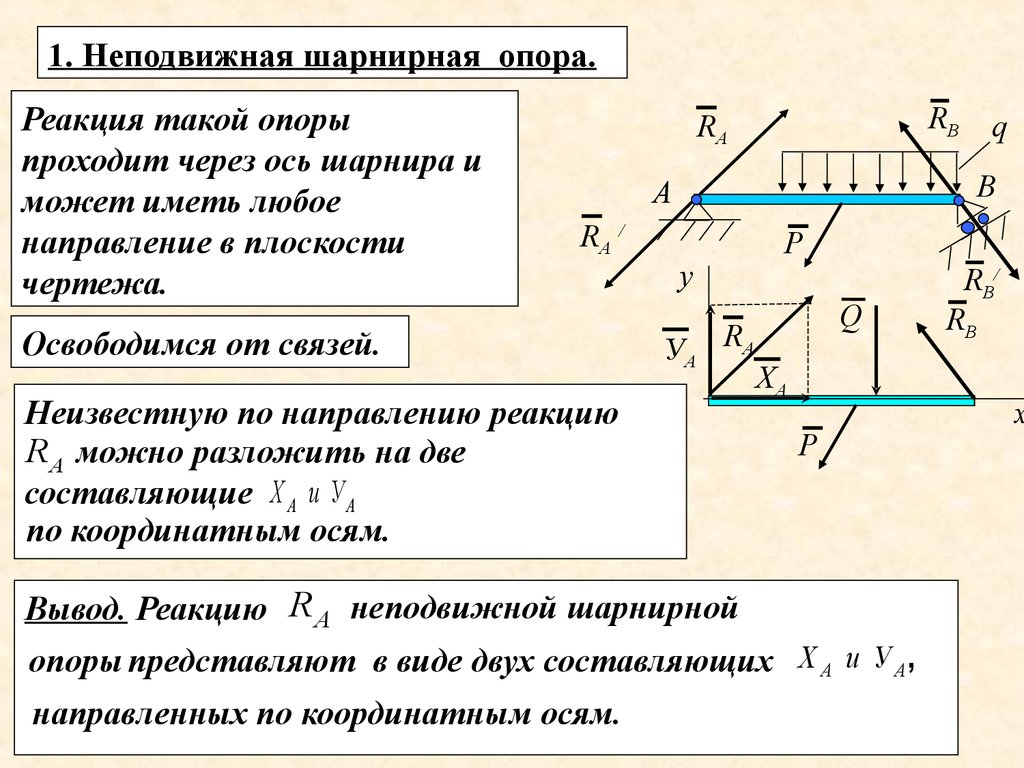
1. Неподвижная шарнирная опора.Реакция такой опоры
проходит через ось шарнира и
может иметь любое
направление в плоскости
чертежа.
RВ
RА
В
А
RА /
Освободимся от связей.
Р
у
УА
Q
RА
Неизвестную
по направлению реакцию
R А можно разложить
на две
составляющие Х А и У А
по координатным осям.
Вывод. Реакцию R А неподвижной шарнирной
ХА
Р
опоры представляют в виде двух составляющих Х А и У А ,
направленных по координатным осям.
q
RВ/
RВ
х
8.
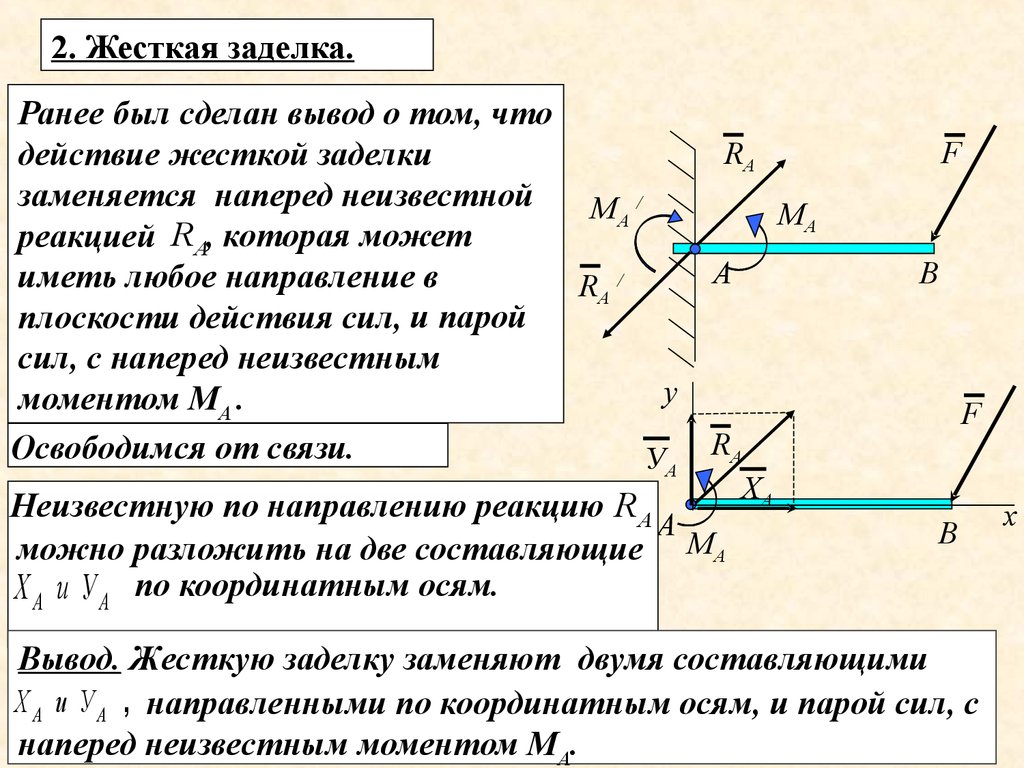
2. Жесткая заделка.Ранее был сделан вывод о том, что
RА
действие жесткой заделки
заменяется
наперед неизвестной
МА /
МА
реакцией R А, которая может
А
иметь любое направление в
RА /
плоскости действия сил, и парой
сил, с наперед неизвестным
у
моментом МА .
Освободимся от связи.
УА RА
ХА
Неизвестную по направлению реакцию R А
А
можно
разложить на две составляющие МА
Х А и У А по координатным осям.
F
В
F
В
Вывод.
Жесткую заделку заменяют двумя составляющими
Х А и У А , направленными по координатным осям, и парой сил, с
наперед неизвестным моментом МА.
х
9.
Решение задач.Применяют алгоритм действий, рассмотренный ранее.
Пример 1. Однородный брус АВ
весом Р опирается концом А на
гладкую горизонтальную плоскость и
выступ D, а концом В – на наклонную
плоскость, образующую с
горизонтальной плоскостью угол α.
Сам брус наклонен под углом β.
Определить силы давления бруса на
обе плоскости и выступ D.
R
D
N1
β
А
В
α
N2 Р
1. Выберем объект равновесия. Брус АВ.
2. Приложим к объекту равновесия заданные силы. Сила P.
3. Освободимся от связей.
10.
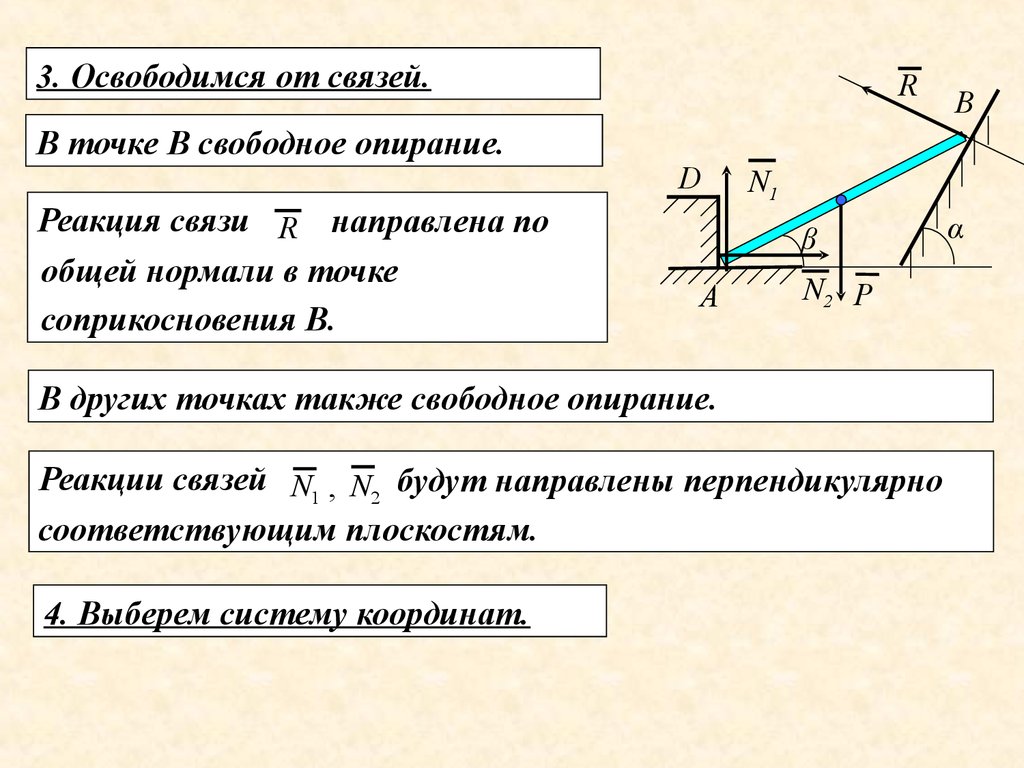
3. Освободимся от связей.В точке В свободное опирание.
Реакция связи R направлена по
общей нормали в точке
соприкосновения В.
R
D
N1
β
А
N2 Р
В других точках также свободное опирание.
Реакции связей N1 , N2 будут направлены перпендикулярно
соответствующим плоскостям.
4. Выберем систему координат.
В
α
11.
Ку
5. Выберем моментную точку.
R
h
Удобно взять точку А, так как в ней
сходится большее число неизвестных
сил (реакций связей).
N1
D
А
β
N2 Р
6. Составим таблицу проекций и моментов.
Fk
N1
N2
P
R
Fkx
0
N2
0
- R sin (α)
Fkу
N1
0
-P
R cos (α)
mА (Fk )
0
0
- P a cos (β) R 2a cos ( γ )
Обозначим АВ = 2 а.
Найдем плечо силы R
относительно точки А: h = АК.
Введем угол γ = α – β. Тогда h = 2 a cos ( γ ).
В
α
х
12.
7. Составим условия (уравнения) равновесия.х: N2 - R sin (α) = 0,
у: N1 – P + R cos (α) = 0,
МА: - P a cos (β) + R 2a cos ( γ ) = 0.
Из последнего уравнения находим
R = (P cos (β))/ 2 cos ( γ )
или
R = (P cos (β))/ 2 cos (α – β ).
Подставляя значение R во второе уравнение, получим
N1 = Р [1 – cos( ) cos( ].)
2 cos( )
Решая первое уравнение, найдем
N2 = Р sin( ) cos( ) .
2 cos( )
13.
Пример 2.d
Симметричная арка загружена
системой сил, приводящейся к
силе Q = 40 кН, приложенной в
точке D, и паре сил с моментом
mD = 120 кН м. Вес арки Р=80 кН.
D
α
mD
P
А
Дано: АВ = а = 10 м, d = 2 м, h = 3
м, α = 600.
Q
В
а
Решение .
1. Выберем объект равновесия.
Арка.
2. Приложим к объекту равновесия заданные силы.
Силы P,
Q и пара сил с моментом mD .
h
14.
3. Освободимся от связей.В точке А подвижный шарнир,
который заменяется одной реакцией
УА , перпендикулярной плоскости, по
которой шарнир может
перемещаться.
у
d
D
mD
P
УА
А
h
УВ
Q
В
а
В точке В неподвижный шарнир, который заменяется двумя
реакциями
Х В и УВ.
4. Выберем систему координат.
5. Выберем две моментные точки для того, что бы
составить вторую форму условий равновесия.
Удобно взять точки А и В, так как в них сходится большее
число неизвестных сил (реакций связей).
х
ХВ
15.
Удобно взять точки А и В, так как вних сходится большее число
неизвестных сил (реакций связей).
6. Составим таблицу проекций и
моментов.
Предварительно разложим силу Q
на две составляющие Q1, Q2.
Модули составляющих:
Q1 = Q cos α , Q2 =Q sin α .
Fk
УА
ХВ
Fkx
0
mА ( Fk)
0
mВ (Fk) - УАа
УВ
P
ХВ
0
0
0
УВ а
0
0
Q1
Q cos α
у
d
D Q1
mD
Q2
P
УА
А
h
УВ
Q
В
х
ХВ
а
Q2
0
- - Q cos(α)h - Q sin(α)d
Рa/2/2
Q sin(α)(а-d)
-Q
Рa/2
cos(α)hh
mD
0
mD
mD
При вычислении момента силы Q была использована
теорема
Вариньона о моменте равнодействующей: m A (Q) m A (Q1 ) m A (Q2 ).
16.
7. Составим уравнения равновесия.∑ Fkx = ХВ + Q cos α = 0,
∑ mА ( Fk) = УВ а - Рa/2 - h Q cos α - d Q sin α + mD= 0,
∑ mВ ( Fk ) = - УАа + Рa/2 - h Q cos α + (а-d) Q sin α + mD= 0.
8. Решим уравнения
Из первого уравнения получим
ХВ = - Q cos α = - 20 кН.
Из второго уравнения найдем
УВ = Р/2 + Q (d sinα + h cosα)/а - mD /а ≈ 40,9 кН.
Из третьего уравнения вычислим
УА = Р/2 + Q [(а - d) sin α - h cos α] /а + mD /а = 73,7 кН.
17.
Модуль полной реакции в опоре В найдется по формуле:RB
Х В2 У В2 45,5 кН
9. Сделаем проверку
Составим уравнение проекций на ось Ау
∑ Fkу = УА + УВ - Q sin α – Р = 114,6 – 114,6 ≡ 0.














 physics
physics








